20 世纪80 年代初,德国的Wille 授提出了形式概念分析理论[1]。到目前,概念格作为形式概念分析的核心数据结构,已经成为一种用于数据组织和数据分析的形式化工具,在数字图书馆及文献检索、软件工程、数据挖掘等许多领域得到了广泛应用[2]。概念格的构造是应用概念格的前提,因此概念格的构造效率就成为人们一直关注的焦点,提出了许多的构造算法。例如:Godin[3]提出了概念格的渐进生成算法;T.B.Ho[4]提出了基于概念格的概念聚类算法;刘宗田等[5]对Godin算法进行了改进;林春杰等[6]提出了基于不完备信息的近似概念格改进的概念格增量构造算法;李海霞[7]提出了基于概念格Hasse图的一种对象渐减式构造算法;崔芳婷等[8]根据用户的需求,把用户感兴趣的背景知识定义为约束,提出一种基于约束的模糊概念格构造算法;刘宏英等[9]基于对多维序列的理解,提出一种新的多维概念格并给出了渐进式构造算法。本文首先将形式背景看成一个0、1的关系矩阵,然后将形式背景化为既约的[10],最后提出了一种基于最大满矩阵来获取概念格的算法。
1 基本概念下面给出形式背景的相关概念。
定义1 [10] 设 U 是对象集合,M 是属性的集合,I 是2个集合 U 与 M 之间的关系,则称三元组 K=(U,M,I) 为一个形式背景(简称背景)。
对于 u∈U,m∈M,(u,m)∈I (或写作 uIm )表示对象 u 具有属性 m 。
定义2 [10] 设 K=(U,M,I) 是一个背景。对于 A⊆U,B⊆M 。令
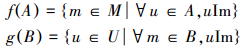
如果 A、B 满足 f(A)=B,g(B)=A,则称二元组 (A,B) 是一个概念。 A 是概念(A,B)的外延, B 是概念 (A,B) 的内涵。
用 L(U,M,I) 表示背景 K=(U,M,I) 上的所有概念集合。
形式背景 K1 如表 1所示,其中对象集 U={u1,u2,u3,u4},属性集 M={a,b,c,d,e,f,g} ,1表示所对应的对象和属性具有关系 I ,0表示所对应的对象和属性不具有关系 I 。
实际上,该形式背景完全由矩阵
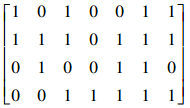
刻画,称此矩阵为形式背景矩阵。
可以验证这个背景的全部概念是:
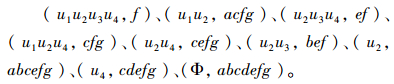
设 K=(U,M,I) 是一个形式背景,H1=(A1,B1),H2=(A2,B2) 是 K 的2个概念,在概念集 L(U,M,I) 上定义关系:
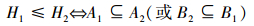
在概念集 LU,M,I 上定义交并运算分别为
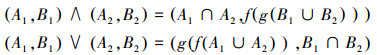
可以证明 L(U,M,I) 对此运算构成完备格,称 L(U,M,I) 为概念格。
为了让形式背景尽可能的简单,下面给出净化背景的定义。
定义3[10] 如果任意满足 f(u)=f(h) 的2个元素 u,h∈U 都有 u=h ,且对任意满足 g(m)=g(n) 的元素 m,n∈M,都有 m=n ,则称背景 (U,M,I)是净化的。
例1 把表 1净化后,得到形式背景 K2 ,如表 2。
为了方便,给具有某种特点的对象或属性一个统一的名称。
定义4 [10] 当 m∉X,但g(m)=g(X),称 m 为可约属性,称 m 产生的属性概念 (g(m),f(g(m))) 为 ∧ 可约的属性概念。
对应地,当 u∉H,但f(u)=f(H) 时,称 u 为可约对象,称 u 产生的对象概念 (g(f(u)),f(u)) 为 ∨ 可约的对象概念。
显然 ∧ 可约的属性与 ∨ 可约的对象是可以删除的。如果所有对象都具有某个属性 m ,则称 m 为“满列属性”;对应地,如果有某个对象 u 具有所有属性,则称 u 为“满行对象”。由定义可得“满列属性”与“满行对象”都是可约的。
如果一个净化背景的每个对象概念都是 ∨ 不可约的,则称这个背景为行既约的。如果一个净化背景的每个属性概念都是 ∧ 不可约的,则称这个背景为列既约的。既是行既约的又是列既约的,则称其是既约的。
例2 把表 2化成既约的,得形式背景 K3,如表 3所示。
这里把属性 f 删除,将属性 c与g 合并成一个属性也不会影响概念格的结构。
由于对具有相同内涵的对象和具有相同外延的属性的各自合并所得的概念格与原概念格同构。所以在生成概念之前可以先把形式背景化为既约的,这样就会使形式背景变得简单些。
2 满矩阵与概念定义5 设 ( U,M,I )为一形式背景,在其对应的形式背景矩阵中,取出对象集 A⊆U 对应的任意行和属性集 B⊆M 对应的任意列组成新的矩阵 MAB,则称 MAB 为形式背景矩阵的子矩阵。
若子矩阵 MAB 的每个元素都为1,则称子矩阵 MAB 为满矩阵。
在满矩阵 MAB 中,规定矩阵 MAB 的列数即 |B| 为矩阵的属性秩,记为 rMAB=|B| ;矩阵 MAB 的行数即 |A| 为矩阵的对象秩,记为 lMAB=|A|,其中|·|表示集合中元素的个数。
定义6 在形式背景矩阵中,对于对象集 A⊆U,如果属性集 B⊆M 有
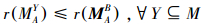
成立,则称 MAB 为对象集 A 对应的最大属性满矩阵。
对偶地,可以定义最大对象满矩阵:
在形式背景矩阵中,对于属性集 B⊆M ,如果对象集 A⊆U 有
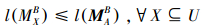
成立,则称 MAB 为属性集 B 对应的最大对象满矩阵。
说明:给定对象集,则其对应的最大属性满矩阵是唯一的;给定属性集,则其对应的最大对象满矩阵是唯一的。
性质1 设( U,M,I )为一形式背景,对任意的对象集 A1⊆A2⊆U ,有
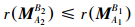
成立,MA1B1、MA2B2 分别为 A1、A2 的最大属性满矩阵。
说明:该性质的依据就是对象集越大,则其具有的共同属性不会多于其子集所具有的共同属性。所以对象集 A2 具有的共同属性应该小于或等于其子集 A1 具有的共同的属性。
性质2 设( U,M,I )为一形式背景,对任意的属性集 B1⊆B2⊆M,有
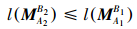
成立,MA1B1,MA2B2 分别为 B1、B2 的最大对象满矩阵。
说明:该性质的依据就是具有的共同属性越多,则其对象集的个数不会增多。所以具有属性集 B2 的对象个数应该小于或等于具有属性集 B1 的对象个数。
定义7 若 (A,B) 为形式概念,则称由对象集 A 所在的行和属性集 B 所在的列组成的矩阵 MAB 为概念矩阵。
定理1 概念矩阵一定是最大属性满矩阵和最大对象满矩阵。
证明:由定义5~7可直接得到结论。反之,定理1不一定成立,即最大属性满矩阵,最大对象满矩阵不一定是概念矩阵。如在例1中,对象 u1 与属性 acfg 组成的子矩阵为最大属性满矩阵,但由概念的定义知 (u1,acfg) 不是形式概念,又对象 u1u2 和属性 a 组成的子矩阵为最大对象满矩阵,但由概念的定义知 (u1u2,a) 不是形式概念,即可得出定理1的逆不成立。
下面给出满矩阵是概念矩阵的一个充分条件:
定理2 若满矩阵 MAB ,既是对象集 A 的最大属性满矩阵,且是属性集 B 的最大对象满矩阵,则满矩阵 MAB 是概念矩阵。
证明 反证,假设满矩阵 MAB 不是概念矩阵,说明 (A,B) 不是概念即 f(A)≠B 或 g(B)≠A 成立。若 f(A)≠B ,则存在对象集 A′⊇A,使 f(A)′=B 成立,也就是说属性集 B 有更大的对象满矩阵,与满矩阵 MAB 是属性集 B 的最大对象满矩阵矛盾;同理可证,若 g(B)≠A ,则存在属性集 B′⊇B,使 g(B)′=A 成立,也就是说对象集 A 有更大的属性满矩阵,与满矩阵 MAB 是对象集 A 的最大属性满矩阵矛盾,即假设不成立,得证。
为了找出形式背景中所有的概念,根据定理1,可以先找出它的所有最大属性满矩阵或最大对象满矩阵,进而根据定理2判断那些满矩阵为概念矩阵,最后得到所有的概念。
3 方法设 (U,M,I) 是一形式背景,显然,它可以看作是一个由0、1表示的矩阵。利用矩阵获得概念的生成算法:
1)将形式背景化为既约背景。首先净化背景,及合并具有相同内涵的对象和具有相同外延的属性,然后删除其内涵等于其他对象内涵交的那些对象,对应地删除其外延等于其他属性外延的交的那些属性,得到的就是既约背景。
2)根据定理1,先找出各形式背景矩阵对应的非零矩阵的最大属性满矩阵或最大对象满矩阵,然后根据定理2判断那些满矩阵是概念矩阵,最后,在概念矩阵中加上矩阵 MGΦ与MΦM 即为所有的概念矩阵。
下面用具体例子说明该算法的过程。
例3 表 3是表 1给出的形式背景 (U,M,I) 的既约背景,它可以表示为一个0,1的关系矩阵,如下所示,现在用给出的概念格生成算法来找出它的概念格:
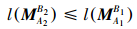
通过上面的矩阵可以计算表 3的概念层次如下:
1)形式背景矩阵对应的非零矩阵的最大属性满矩阵有:
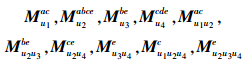
这里,ac 代表集合 {a,c} ,余同。
2)由定理2得出概念矩阵有:
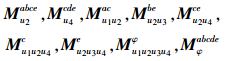
最后,得到概念所有的概念:
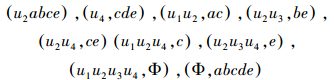
另外,可以先找出所有的最大对象满矩阵,再根据定理2得到概念矩阵,进而得到所有的概念。
为了进一步说明该算法的有效性,给出实例:
例4 [11] 软件的结构设计主要是针对软件的数据结构模式,在需求分析的基础上,通过合理化组织,加以分析设计,从而得出设计的方法。下面假设一个系统,这个系统包括6个过程(分别假设为 P1,P2,P3,P4,P5,P6 )以及一个包含9个字段的记录。利用相关的分析器可以分析出每个项目在每一个过程中的使用情况(“1”表示使用),如表 5所示。用上面算法构造出对应的概念。
根据上文给出的定义,删除可约对象 β ,合并相同对象后,可以写出表 4对应的既约背景如表 5。
| 参数 | P1 | P2 | P3 | P4 | P5 | P6 |
| NAME:α | 1 | 0 | 0 | 0 | 0 | 1 |
| TITLE:β | 1 | 0 | 0 | 0 | 0 | 0 |
| INTTIAL:γ | 1 | 0 | 0 | 0 | 1 | 0 |
| PREFIX:δ | 1 | 0 | 0 | 0 | 1 | 0 |
| NUMBER:ε | 0 | 0 | 0 | 1 | 0 | 1 |
| NUMBER-EXT:ζ | 0 | 0 | 0 | 1 | 0 | 1 |
| ZIPCD:θ | 0 | 0 | 0 | 1 | 0 | 1 |
| SIREFT:ι | 0 | 0 | 1 | 1 | 0 | 0 |
| CITY:κ | 0 | 1 | 0 | 1 | 0 | 0 |
| 参数 | P1 | P2 | P3 | P4 | P5 | P6 |
| NAME:α | 1 | 0 | 0 | 0 | 0 | 1 |
| INTTIAL:γ | ||||||
| PREFIX:δ | 1 | 0 | 0 | 0 | 1 | 0 |
| NUMBER:ε | ||||||
| NUMBER-EXT:ζ | 0 | 0 | 0 | 1 | 0 | 1 |
| ZIPCD:θ | ||||||
| SIREFT:ι | 0 | 0 | 1 | 1 | 0 | 0 |
| CITY:κ | 0 | 1 | 0 | 1 | 0 | 0 |
下面写出它既约背景对应的关系矩阵:
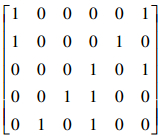
通过上面的矩阵可以计算表 5的概念层次如下:
1)形式背景矩阵对应的非零矩阵的最大属性满矩阵有:
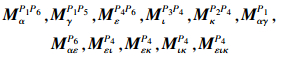
2)由定理2得出概念矩阵有:
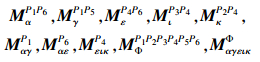
3)最后,得到概念所有的概念:
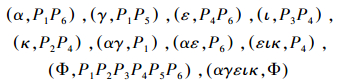
目前,已有不少概念格的建格算法,本文从矩阵的角度出发,利用矩阵与概念之间的联系,定义了一种新的基于概念的矩阵——最大满矩阵,找出了最大满矩阵与概念之间的联系,进而得出了一种基于矩阵的概念格生成算法,具体例子说明该算法是有效的。
| [1] | WILLE R. Restructuring lattice theory:an approach based on hierarchies of concepts[M]//RIVAL I. Ordered Sets. Berlin Heidelberg:Springer, 1982:445-470. |
| [2] | OOSTHULZEN G D. The application of concept lattice to machine learning[R]. South Africa:University of Pretoria, 1996. |
| [3] | GODIN R, MISSAOUI R, ALAOUI H. Incremental concept formation algorithms based on Galois(concept) lattices[J]. Computational Intelligence, 1995, 11(2):246-267. |
| [4] | HO T B. Incremental conceptual clustering in the framework of Galois lattice[C]//LU H, LIU H, MOTODA H. KDD:Techniques and Applications. Singapore:World Scientific, 1997:49-64. |
| [5] | 谢志鹏, 刘宗田. 概念格的快速渐进式构造算法[J]. 计算机学报, 2002, 25(5):490-496.XIE Zhipeng, LIU Zongtian. A fast incremental algorithm for building concept lattice[J]. Chinese Journal of Computers, 2002, 25(5):490-496. |
| [6] | 林春杰, 普杰信, 张瑞玲. 近似概念格及其增量构造算法研究[J]. 计算机应用研究, 2012, 29(1):25-27.LIN Chunjie, PU Jinxin, ZHANG Ruilin. Approximation concept lattice and incremental constructing algorithm[J]. Application Research of Computers, 2012, 29(1):25-27. |
| [7] | 李海霞. 基于Hasse图的概念格的一种渐减式构造算法[J]. 河南科技学院学报, 2015, 43(3):57-60, 66.LI Haixia. A decreasing algorithm of concept lattice based on Hasse diagram[J]. Journal of Henan Institute of Science and Technology, 2015, 43(3):57-60, 66. |
| [8] | 崔芳婷, 王黎明, 张卓. 基于约束的模糊概念格构造算法[J]. 计算机科学, 2015, 42(8):288-293, 318.CUI Fangting, WANG Liming, ZHANG Zhuo. Construction algorithm of fuzzy concept lattice based on constraints[J]. Computer Science, 2015, 42(8):288-293, 318. |
| [9] | 刘宏英, 郭显娥, 胡小珍. 多维概念格及其构造算法[J]. 计算机工程与应用, 2012, 48(12):96-99, 111.LIU Hongying, GUO Xian'e, HU Xiaozhen. Multidimensional concept lattice and constructing algorithm[J]. Computer Engineering and Applications, 2012, 48(12):96-99, 111. |
| [10] | 马垣, 曾子维, 迟呈英, 等. 形式概念及其新进展[M]. 北京:科学出版社, 2010:11-24. |
| [11] | 蒋平, 任胜兵, 林鹃. 形式概念分析在软件工程中的应用[J]. 计算机技术与发展, 2008, 18(4):127-129, 213.JIANG Ping, REN Shengbing, LIN Juan. Using formal concept analysis for software engineering[J]. Computer Technology and development, 2008, 18(4):127-129, 213. |



