随着水污染问题的日趋严重,污水排放不但严重影响着居民的日常生活,给人们出行带来不便,而且直接威胁到了所有生物的生存,破坏了大自然的生态平衡,从经济角度上看,被污染后的清洁水将会失去原有的使用功能,造成了经济上的巨大损失。为了降低污水的排放量,有效地进行污水处理已经迫在眉睫。从目前的运行情况来看,污水处理过程中存在的一个问题是运行成本居高、能源消耗大。因此,研究节能降耗技术是当前实现污水处理过程最优控制亟待解决的问题。
污水处理过程是一个具有高度非线性、大滞后、大时变、多变量耦合等特点的复杂系统,在出水水质达标的前提下降低能耗是非常具有挑战性的[1],部分学者对其进行了研究并取得了阶段性的成果。Zhang等[2]根据进水和出水氨浓度,采用串级控制策略对溶解氧浓度进行了优化控制,不仅降低了能耗,还改善了出水氨氮和总氮浓度。近年来,模型预测控制得到了广泛的应用[3, 4, 5, 6]。Ostace等[3]基于改进的ASM1设计了2种控制策略,均采用模型预测控制算法,策略一是针对溶解氧和硝态氮的闭环控制,策略二在对溶解氧和硝态氮控制的基础上增加了第5分区的氨的闭环控制,有效降低了运行费用,改善了出水水质。由于污水处理过程参数的时变特性及生化反应过程的不确定性[7, 8, 9],导致建立精确的污水处理机理模型存在一定难度,而模型的精确度对MPC的控制精度有很大影响。Iqbal等[10]采用非主导排序遗传算法解决污水处理过程中的优化问题,而遗传算法的计算量大,全局收敛速度较慢,同时其优化结果的精度受编码长度的控制。由于粒子群不需要复杂的交叉变异,算法简单、参数少、易于实现,史雄伟等[11]提出一种基于分工策略的粒子群优化算法,用于动态优化底层PID控制器的最佳设定值,达到了出水水质高、能量消耗少的目的。无论是遗传算法还是粒子群算法,像这种进化计算的智能搜索算法虽然能够很好地解决优化问题,但是在搜索过程中需要的样本量非常大,不能实时更新优化信号,更适用于离线优化。
Vrbie等[12]采用策略迭代的方法,通过对当前控制策略的性能评估来对控制策略进行改善,并指出一个智能控制器应该是可以根据外界环境的变化而动态改变控制策略的。文中设计了一种自适应在线优化控制器,通过神经网络预测未来的性能指标函数值,然后将其传递给神经网络优化层,根据系统的环境状态以及上一时刻的控制变量设定值来优化预测的指标函数值,使其达到最小,从而产生新的设定值送到底层控制器进行跟踪,实现污水处理过程的优化控制。
1 污水处理过程模型为了对不同的控制策略进行比较,欧盟科学技术合作组织(COST)和国际水协合作共同提出的一个基准仿真模型(benchmark simulation model 1,BSM1)[13],它定义了一种污水处理的设备布局、相应的仿真模型、污水负荷、仿真步骤和仿真结果的评价标准,BSM1的总体布局如图 1所示。
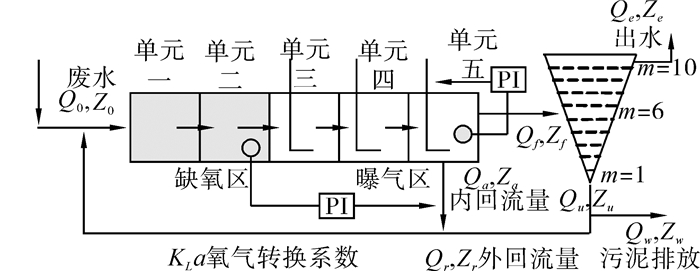 |
| 图 1 BSM1的设备布局图 Fig. 1 The equipment layout of BSM1 |
该模型由生化反应池和二沉池2部分组成,生化反应池的前2个单元为缺氧区,后3个单元为好氧区,缺氧区2个单元的体积V1=V2=1 000 m3,好氧区3个单元的体积V3=V4= V5=1 333 m3。每个单元中,Qk表示流量;Zk表示各组分的质量分数,Z=(SI,SS,XI,XS,XBH,XP,SNO,SNH,SND,XND,SALK);rk=vk1ρ1+vk2ρ2+…+vk8ρ8表示各组分的反应速率;各单元物料平衡方程为如下:
单元一(k=1):
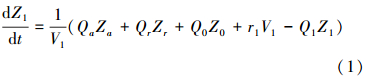
式中:Qa、Qr、Q0分别为混合液回流量、污泥回流量和入水流量;Q1 =Qa +Qr+Q0。
其他单元(k=2~5):

式中:Qk=Qk-1。
由于溶解氧浓度受曝气量的影响,因此其物料平衡方程比较特殊,如式(3)所示:

式中:溶解氧的饱和浓度SO,sat=8 mg/L。
在BSM1中,控制变量是第5分区的溶解氧和第2分区的硝态氮浓度,如果溶解氧浓度过高,回流到厌氧区的溶解氧浓度就会升高,不利于反硝化过程,同时会使曝气能耗偏高,如果溶解氧过低,容易发生污泥膨胀;同样维持合适的硝态氮浓度,才能够高效利用缺氧区的反硝化能力,同时避免过高的内循环回流量带来的问题,提高脱氮去除率并减少动力消耗。因此动态调整溶解氧和硝态氮的设定值能有效提高污水处理效率,降低能耗。
2 基于ESN的污水处理优化控制 2.1 优化问题描述一般情况下,优化的目标是寻找一组能够使得性能指标达到最大或者最小的设定值优化序列。表示如下:
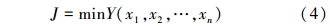
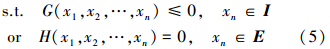
式中:Y(x)表示需要优化的目标函数,G(x)≤0,xi∈I和H(x)=0,xi∈E分别表示优化过程中的不等式和等式约束条件。其中,I为不等式约束指标集,E为等式约束指标集。
Brdys等[5]指出污水处理厂的控制意义在于保证其稳定运行,在使出水水质达标的同时尽量减少能耗。因此,污水处理过程优化是一个多目标优化的过程,不仅要考虑出水水质是否达标,还要考虑是否能节省运行费用。基于以上,文中定义优化的性能指标函数如式(6)所示:
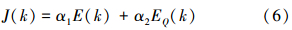
式中:α1、α2为衡量能耗E和出水水质EQ的权重因子,α1、α2∈[0, 1],并且α1+α2=1,E为一个优化周期内的总能耗,是曝气能耗EA和泵送能耗EP之和,EQ表示一个优化周期向受纳水体排放污染物需要支付的罚款,其大小与出水水质的好坏相关联,出水水质越好,EQ越小。E、EA、EP、EQ的表达式分别如(7)、(8)、(9)、(10)所示:
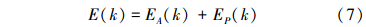
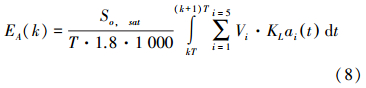


式中:k为整数变量,T1=1/(1 000·T),T为优化周期,KLai为氧气传递速率,Qa为混合液回流量,Qr为污泥回流量,Qw为污泥排放量,Bi为不同污染物对出水水质EQ影响的权重因子。其具体取值如表 1。
在优化过程中,约束条件包括以下几个:
1)物料平衡的约束:
见式(1)~式(3);
2)出水水质约束:

3)执行器约束:
控制变量:
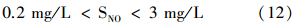
操作变量:
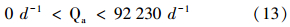
基于ESN的在线优化控制系统如图 2所示,包括2个ESN:预测ESN和优化ESN。其中,预测ESN用来估计未来的性能指标函数,优化ESN用来优化预测的性能指标函数。图中,S(k)表示输入状态变量,R(k)为当前时刻的设定值,系统根据系统状态给定一个初始设定值,预测ESN能够估计未来时刻的性能指标函数,然后优化ESN根据k+1时刻的状态及k时刻的设定值,来使预测出的性能指标函数达到最小,进而产生新的设定值传递给底层的PID控制器。
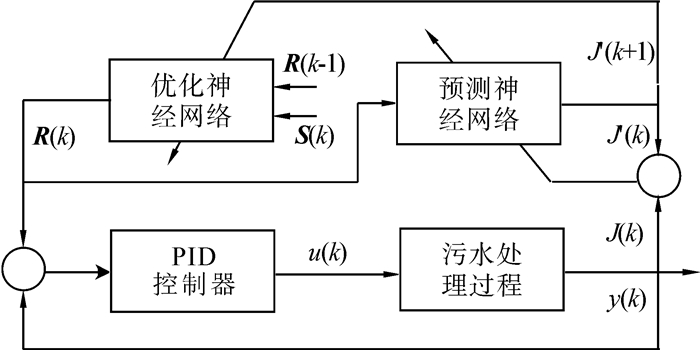 |
| 图 2 优化控制系统结构图 Fig. 2 The structure of optimal control system |
由于回声状态网络(echo state network,ESN)具有非常强大的非线性逼近能力,文中利用ESN来逼近未来时刻的性能指标函数,性能指标预测模型可以表示为
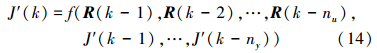
式中:J′为性能指标,R为变量设定值,f为系统对应函数。
设系统的输入为
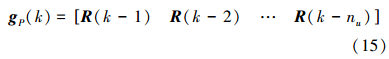
则ESN的动态储备池输出为
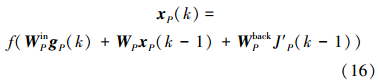
式中:xP为动态储备池输出,WPin、WP、WPback分别为预测网络的输入、内部状态、输出到内部状态的连接权值矩阵,f取为Sigmoid函数。ESN的输出为性能指标函数:
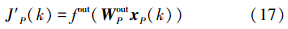
式中:J′P为预测的性能指标,WPout为内部状态储备池到输出的连接权值矩阵,fout取为线性函数。调整预测模型网络权值的指标函数为

权值调整公式为
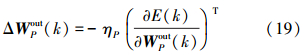
式中:ηP为预测网络的学习速率。
文中采用递推预测,利用式(14)构建的模型即可得到k+1时刻的预测输出。

文中的优化控制系统上层采用神经网络优化方法,根据污水处理过程k时刻的状态以及k-1时刻的设定值,通过优化性能指标预测模型的输出,即k+1时刻的性能指标值J′ (k+1),来调整优化神经网络的权值。同样,神经网络优化模型采用ESN,其输入为
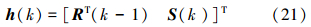
ESN的动态储备池输出为

式中:x为优化网络的动态储备池输出,Win、W、Wback分别为优化网络的输入、内部状态、输出到内部状态的连接权值矩阵。ESN的输出为设定值:

式中:Wout为优化网络的内部状态储备池到输出的连接权值矩阵。权值调整公示如式(24)所示[14]。
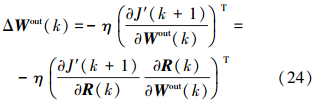
式中: η为优化网络的学习速率,∂J′(k+1)/∂R(k)可以由性能指标预测模型(16)和(17)求得,∂R(k)/∂Wout (k)可以通过优化神经网络(23)获得,随着神经网络权值的调整,△∂Wout (k)将会趋于0,即∂J′(k+1)/∂R(k)会趋于0,因此得到了当J′ (k+1)最小时控制变量的设定值。
3 实验研究文中的实验是基于BSM1进行的,它是从实际系统抽离出来公认的一个基准仿真模型,在MATLAB环境下搭建。BSM1包含了晴好天气、雨天和暴雨天气3个数据文件,每个文件均为14 d的进水信息,该实验是在晴好天气下进行的。用于预测性能指标的ESN和用于优化的ESN内部神经元均为45个,性能指标中α1、α2分别取为0.8、0.2,优化ESN 中输入S(k)为k时刻的状态,包括:进水溶解氧浓度(SO)、进水硝态氮浓度(SNO)、进水氨浓度(SNH)、进水可溶性有机氮(SND)、进水不可溶性有机氮(XND)和进水流量(Q0),优化周期为2 h,输出为设定值,然后将其传递给底层的PID控制器进行跟踪,PID参数分别取为:KPO=200,KIO=150,KDO=5,KPNO=80 000,KINO=7 000,KDNO=400,图 3和图 4分别为溶解氧浓度和硝态氮浓度的优化结果,溶解氧浓度和硝态氮浓度随着外界环境(进水流量和入水组分)的变化呈现周期性变化。将神经网络优化控制与BSM1中缺省的PID闭环控制策略(溶解氧浓度和硝态氮浓度的设定值为固定值,分别为2 mg/L和1 mg/L)相比较,出水BOD、出水COD以及TSS的对比分别如图 5~7所示,出水氨氮、总氮的对比结果如图 8和图 9,表 2为2种控制策略下的平均出水水质比较。以上结果均显示,出水BOD、出水COD及出水TSS变化不大,而随着对溶解氧浓度和硝态氮浓度的优化,溶解氧浓度的平均设定值相较于闭环控制的溶解氧浓度2 mg/L降低了,如图 3所示。式(21)和式(22)为硝化过程的反应方程式,式(23)为反硝化过程的反应方程式,溶解氧浓度的降低影响了硝化过程,所以表 2中氨氮的浓度升高了。
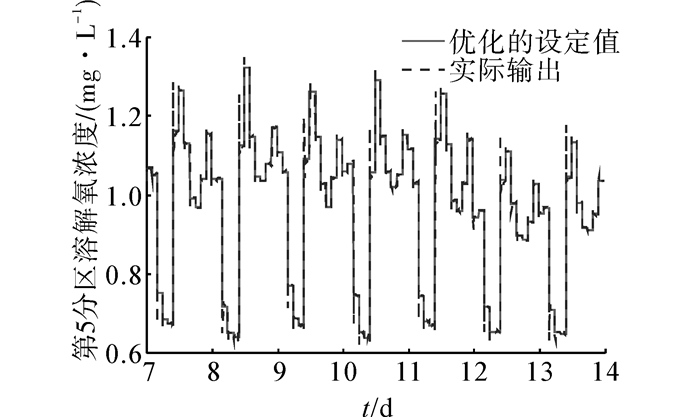 |
| 图 3 溶解氧优化效果 Fig. 3 Optimization results of the dissolved oxygen concentration |
 |
| 图 4 硝态氮优化效果 Fig. 4 Optimization results of the nitrate concentration |
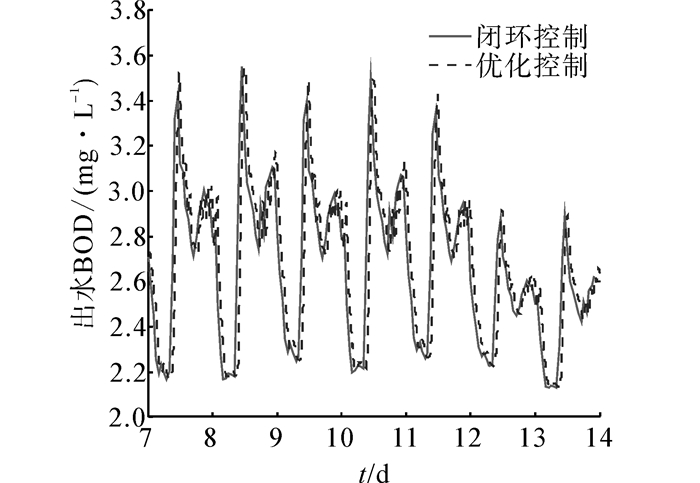 |
| 图 5 出水BOD的效果比较 Fig. 5 Comparison results of effluent BOD |
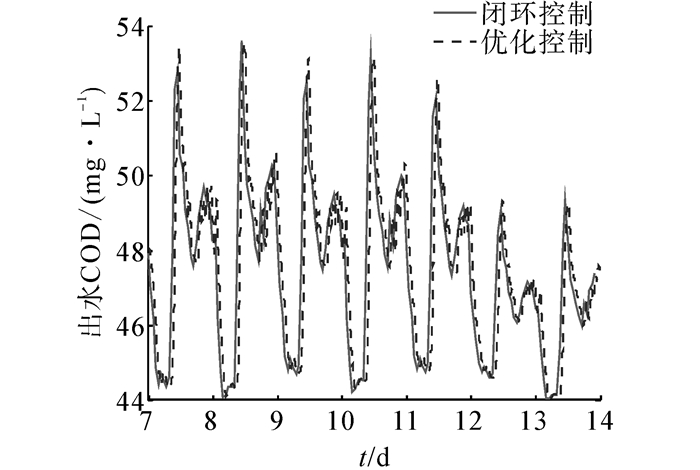 |
| 图 6 出水COD的效果比较 Fig. 6 Comparison results of effluent COD |
 |
| 图 7 出水TSS的效果比较 Fig. 7 Comparison results of effluent TSS |
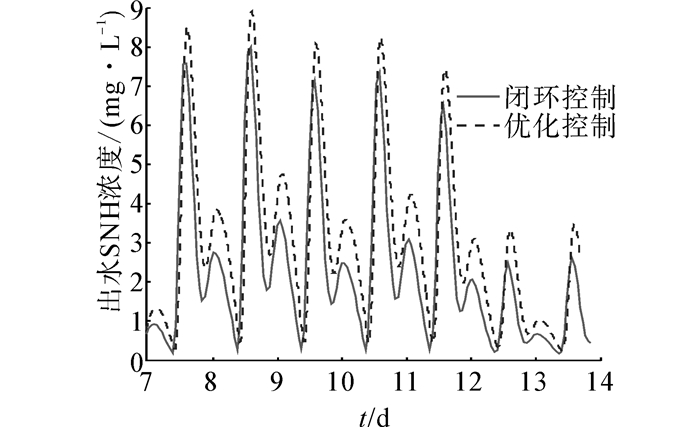 |
| 图 8 出水氨氮的效果比较 Fig. 8 Comparison results of effluent SNH |
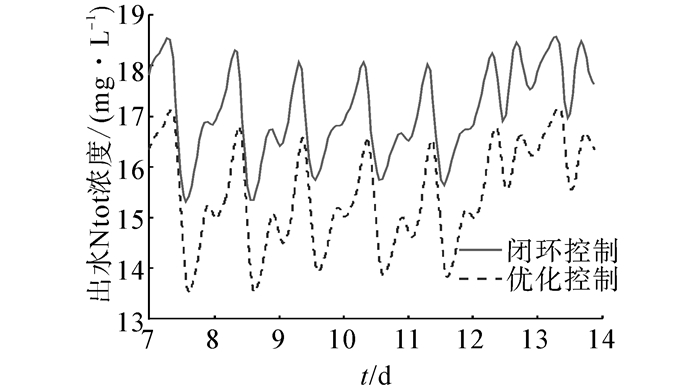 |
| 图 9 出水总氮的效果比较 Fig. 9 Comparison results of effluent Ntot |
| 控制 策略 | BOD5/ gCOD·m-3 | COD/ gCOD·m-3 | SNH/ gN·m-3 | Ntot/ gN·m-3 | TSS/ gSS·m-3 |
| 闭环控制 | 2.676 3 | 47.511 4 | 2.303 7 | 16.800 6 | 12.621 9 |
| 优化控制 | 2.678 4 | 47.523 5 | 2.872 3 | 15.601 4 | 12.591 7 |

溶解氧浓度的降低导致回流到缺氧区的溶解氧浓度降低,有利于反硝化过程的进行,进而总氮浓度降低了。
表 3中优化控制与闭环控制相比,虽然EQ增大了0.881%,但是表 2中的出水水质仍然满足国家排放标准,优化控制比闭环控制的泵送能耗PE增加了12.77%,曝气能耗AE减少了4.958%,致使总能耗(AE与PE之和)减少3.906%,达到了较好的节能效果。在污水处理过程中,AE会占到总运行费用的60%以上或是更多[15],优化控制后的溶解氧浓度设定值的平均值小于闭环回路控制所采取的经验设定值(2 mg/L),需氧量减少,AE明显降低;硝态氮浓度影响PE的大小,优化控制中的平均设定值大于闭环控制的经验值(1 mg/L),因此PE升高。而曝气能耗在总能耗占的比重较大,最终运行成本降低。
| 控制 策略 | EQ/ kgpoll.units·d-1 | AE/ kWh·d-1 | PE/ kWh·d-1 | Energy/ kWh·d-1 |
| 闭环控制 | 6 080.9 | 3 677.016 | 232.455 | 3 909.5 |
| 优化控制 | 6 134.5 | 3 494.7 | 262.130 8 | 3 756.8 |
文中以BSM1为平台,综合考虑出水水质、曝气能耗和泵送能耗多个优化目标,对第5分区的溶解氧浓度和第2分区的硝态氮浓度进行了神经网络在线优化控制,能够根据环境状态变化来动态调整控制变量设定值,解决了模型预测控制中建立的机理模型不精确问题,克服了智能优化算法计算复杂度大、不能实时更新优化控制信号的缺点。实验结果表明,基于ESN的污水处理过程节能优化控制策略,不但能够满足国家出水水质达标的要求,而且能够动态优化控制参量的设定值,最终实现降低运行成本的目的。
| [1] | HAIMIA H, MULAS M, CORONA F, et al. Data-derived soft-sensors for biological wastewater treatment plants:an overview[J]. Environmental Modelling and Software, 2013, 47:88-107. |
| [2] | ZHANG Ping, YUAN Mingzhe, WANG Hong. Improvement of nitrogen removal and reduction of operating costs in an activated sludge process with feedforward-cascade control strategy[J]. Biochemical Engineering Journal, 2008, 41(1):53-58. |
| [3] | OSTACE G S, CRISTEA V M, AGACHI P S. Cost reduction of the wastewater treatment plant operation by MPC based on modified ASM1 with two-step nitrification/denitrification model[J]. Computers and Chemical Engineering, 2011, 35(11):2469-2479. |
| [4] | PIOTROWSKI R, BRDYS M A, KONARCZAK K, et al. Hierarchical dissolved oxygen control for activated sludge processes[J]. Control Engineering Practice, 2008, 16(1):114-131. |
| [5] | BRDYS M A, GROCHOWSKI M, GMINSKI T, et al. Hierarchical predictive control of integrated wastewater treatment systems[J]. Control Engineering Practice, 2008, 16(6):751-767. |
| [6] | HOLENDA B, DOMOKOS E, RÉDEY Á, et al. Dissolved oxygen control of the activated sludge wastewater treatment process using model predictive control[J]. Computers and Chemical Engineering, 2008, 32(6):1270-1278. |
| [7] | 薄迎春, 乔俊飞. 启发式动态规划在污水处理过程控制中的应用[J]. 控制理论与应用, 2013, 30(7):828-833. BO Yingchun, QIAO Junfei. Application of heuristic dynamic programming to wastewater treatment process control[J]. Control Theory and Applications, 2013, 30(7):828-833. |
| [8] | 丛秋梅, 柴天佑, 余文, 等. 污水处理过程的递阶神经网络建模[J]. 控制理论与应用, 2009, 26(1):8-14. CONG Qiumei, CHAI Tianyou, YU Wen, et al. Modeling wastewater treatment plant via hierarchical neural networks[J]. Control Theory and Applications, 2009, 26(1):8-14. |
| [9] | JOUANNEAU S, RECOULES L, DURAND M J, et al. Methods for assessing biochemical oxygen demand(BOD):a review[J]. Water Research, 2014, 49:62-82. |
| [10] | IQBAL J, GURIA C. Optimization of an operating domestic wastewater treatment plant using elitist non-dominated sorting genetic algorithm[J]. Chemical Engineering Research and Design, 2009, 87(11):1481-1496. |
| [11] | 史雄伟, 乔俊飞, 苑明哲. 基于改进粒子群优化算法的污水处理过程优化控制[J]. 信息与控制, 2011, 40(5):698-703. SHI Xiongwei, QIAO Junfei, YUAN Mingzhe. Optimal control for wastewater treatment process based on improved particle swarm optimization algorithm[J]. Information and Control, 2011, 40(5):698-703. |
| [12] | VRABIE D, LEWIS F. Neural network approach to continuous-time direct adaptive optimal control for partially unknown nonlinear systems[J]. Neural Networks, 2009, 22(3):237-246. |
| [13] | COPP J B. The COST simulation benchmark:description and simulator manual[R]. Luxembourg:Office for Publications of the European Community, 2001. |
| [14] | QIAO Junfei, BO Yingchun, CHAI Wei, et al. Adaptive optimal control for a wastewater treatment plant based on a data-driven method[J]. Water Science and Technology, 2013, 67(10):2314-2320. |
| [15] | CHACHUAT B, ROCHE N, LATIFI M. Long-term optimal aeration strategies for small-size alternating activated sludge treatment plants[J]. Chemical Engineering and Processing:Process Intensification, 2005, 44(5):591-604. |



