2. 南京大学 计算机软件新技术国家重点实验室, 江苏 南京 210093;
3. 辽宁师范大学 数学学院, 辽宁 大连 116081
2. State Key Laboratory for Novel Software Technology, Nanjing University, Nanjing 210093, China;
3. School of Mathematics, Liaoning Normal University, Dalian 116081, China
Zadeh在1965年提出了模糊集理论[1],而后Atanassov对模糊集理论进行了拓展,提出了直觉模糊集理论[2, 3]。徐扬等在20世纪80年代末提出了格蕴涵代数,使不确定性的描述有了更系统化的结构,并讨论了相应的性质[4, 5],这样既能处理可比较信息,又能处理不可比较信息,从而可以更有效地描述和处理人的推理、判断和决策中的不确定性,为不确定性推理和近似推理提供了新的途径和理论基础。
近年来,不确定性推理技术引起了人们的重视,许多学者在不确定推理方面做出了巨大的贡献[6, 7]。雷英杰等在直觉模糊逻辑方面提出真值限定的直觉模糊推理方法、直觉模糊逻辑的插值推理方法和直觉模糊近似推理方法[8, 9, 10];徐扬等在语言真值格蕴涵代数方面提出基于概念格的语言真值不确定性推理和基于语言真值格值一阶逻辑的不确定性推理[11, 12];此外,邹丽等在格蕴涵代数方面提出基于十元格蕴涵代数的知识表示方法、基于十八元语言值模糊相似矩阵的聚类方法和基于六元格值命题逻辑的语言真值归结方法,在直觉模糊推理方面提出语言真值直觉模糊逻辑的知识推理方法[13, 14, 15, 16, 17]。
目前,将直觉模糊推理方法运用在语言真值直觉模糊格中的研究还比较少,并且在现有的语言真值直觉模糊推理方法中,只考虑了正反两方面信息的处理,而忽略了犹豫信息,增加了推理过程中信息的损失。因此,为了解决上述问题,本文提出基于真值限定的语言真值直觉模糊推理方法。
1 预备知识 1.1 直觉模糊集在直觉模糊集中,Atanassov采用隶属度和非隶属度表示对象隶属于某一集合的程度。形式地,直觉模糊集定义为
定义1[2] 设X是一个给定论域,则X上的一个直觉模糊集
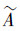 为
为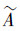 ={<x,u(x),v(x)>|x∈X} ,其中 u(x):X
→[0, 1]和 v(x):X→[0, 1] 分别代表
A的隶属函数u(x)和非隶属函v(x),且对于A上的所有x∈X,0
≤u(x)+v(x)≤1成立。
={<x,u(x),v(x)>|x∈X} ,其中 u(x):X
→[0, 1]和 v(x):X→[0, 1] 分别代表
A的隶属函数u(x)和非隶属函v(x),且对于A上的所有x∈X,0
≤u(x)+v(x)≤1成立。
在直觉模糊集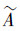 中,πA(x)=1-uA(x)-vA(x)(
∀x∈U)称为x隶属于
中,πA(x)=1-uA(x)-vA(x)(
∀x∈U)称为x隶属于
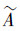 的犹豫度。在Zadeh
的模糊集中,若uA(x)是x隶属于
A的隶属度,则1-uA(x)是非隶属度,即uA(x)+1-uA(x)=1。从这个角度来看,直觉模糊集是模糊集的推广。
的犹豫度。在Zadeh
的模糊集中,若uA(x)是x隶属于
A的隶属度,则1-uA(x)是非隶属度,即uA(x)+1-uA(x)=1。从这个角度来看,直觉模糊集是模糊集的推广。
注:在直觉模糊集
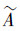 中,犹豫度πA(x)满足πA(x)=1-uA(x)-vA(x),当uA(x)或vA(x)增大或减小时,πA(x)相应的减小或增大,并且πA(x)变化的范围与uA(x)或vA(x)变化的范围相一致。
中,犹豫度πA(x)满足πA(x)=1-uA(x)-vA(x),当uA(x)或vA(x)增大或减小时,πA(x)相应的减小或增大,并且πA(x)变化的范围与uA(x)或vA(x)变化的范围相一致。
为了更加具体地研究语言真值直觉模糊代数,在已建立的语言真值直觉模糊代数(LTV-IFA)的框架下[17],将介绍六元语言真值直觉模糊代数(6LTV-IFA)。
设语气词集H ={hi|i=1,2,3},h1<h2<h3,其中语气词h1=“稍微”,h2=“一般”,h3=“非常”,元语言真值集C={cj|j=1,2},c1=t,即“真”,c2=f,即“假”。令六元语言真值格蕴涵代数LV(3×2)={A,B,C,J,K,S} 中A=(h3,t),B=(h2,t),C=(h1,t),J=(h3,f),K=(h2,f),S=(h1,f)。
定义2[13] 在六元语言真值格蕴涵代数LV(3×2)={A,B,C,J,K,S} 中,对任意(hi,t),(hj,f)∈LV(3×2),则((hi,t),(hj,f)) 称为一个六元语言真值直觉模糊对,且 ((hi,t),(hj,f)) 满足 (hi,t)′≥(hj,f)。
定义3[13] LI6= (LI6,∪,∩)是六元语言真值直觉模糊代数即6LTV-IFA,其结构如图 1所示。
在六元语言真值直觉模糊格LI6上,(A,J) 和 (C,S) 分别为LI6的最大元和最小元。
对任意((hi,t),(hj,f)),((hk,t),(hl,f))∈LI6,其中,i,j,k,l∈1,2,3,定义 “→”、“∨”、“∧”和“′”4种运算如下:
1)((hi,t),(hj,f))→((hk,t),(hl,f))=((hmin(3,3-i+k,3-j+l),t),(hmin(3,3-i+l),f));
(2)((hi,t),(hj,f))∨((hk,t),(hl,f))=((hmax( i,k),t),(hmax(j,l),f));
3)((hi,t),(hj,f))∧((hk,t),(hl,f))=((hmin(i,k),t),(hmin(j,l),f));
4)((hi,t),(hj,f))′=((h3-j+1,t),(h3-i+1,f))。
具体地,LI6中的运算如表 1~3所示。
| 元 | (A,J) | (B,K) | (C,S) | (B,J) | (C,K) | (C,J) |
| (A,J) | (A,J) | (B,K) | (C,S) | (B,J) | (C,K) | (C,J) |
| (B,K) | (A,J) | (A,J) | (B,K) | (A,J) | (B,J) | (B,J) |
| (C,S) | (A,J) | (A,J) | (A,J) | (A,J) | (A,J) | (A,J) |
| (B,J) | (A,J) | (B,J) | (C,K) | (A,J) | (B,J) | (B,J) |
| (C,K) | (A,J) | (A,J) | (B,J) | (A,J) | (A,J) | (A,J) |
| (C,J) | (A,J) | (B,J) | (C,J) | (A,J) | (B,J) | (A,J) |
| 元 | (A,J) | (B,K) | (C,S) | (B,J) | (C,K) | (C,J) |
| (A,J) | (A,J) | (A,J) | (A,J) | (A,J) | (A,J) | (A,J) |
| (B,K) | (A,J) | (B,K) | (B,K) | (B,J) | (B,K) | (B,J) |
| (C,S) | (A,J) | (B,K) | (C,S) | (B,J) | (C,K) | (C,J) |
| (B,J) | (A,J) | (B,J) | (B,J) | (B,J) | (B,J) | (B,J) |
| (C,K) | (A,J) | (B,K) | (C,K) | (B,J) | (C,K) | (C,J) |
| (C,J) | (A,J) | (B,J) | (C,J) | (B,J) | (C,J) | (C,J) |
| 元 | (A,J) | (B,K) | (C,S) | (B,J) | (C,K) | (C,J) |
| (A,J) | (A,J) | (B,K) | (C,S) | (B,J) | (C,K) | (C,J) |
| (B,K) | (B,K) | (B,K) | (C,S) | (B,K) | (C,K) | (C,K) |
| (C,S) | (C,S) | (C,S) | (C,S) | (C,S) | (C,S) | (C,S) |
| (B,J) | (B,J) | (B,K) | (C,S) | (B,J) | (C,K) | (C,J) |
| (C,K) | (C,K) | (C,K) | (C,S) | (C,K) | (C,K) | (C,K) |
| (C,J) | (C,J) | (C,K) | (C,S) | (C,J) | (C,K) | (C,J) |
定义4 在语言真值直觉模糊格中,对任意语言真值直觉模糊对((hi,t),(hj,f))∈LI6,πL6=πk|0≤k≤2,若 Π :LI<6→πL6满足Π((hi,t),(hj,f)) =πj-i且0≤i≤j≤2,则称Π((hi,t),(hj,f))为语言真值直觉模糊犹豫度。
在六元语言真值直觉模糊格中,语言真值直觉模糊犹豫度有3种:即π0代表“没有犹豫”,π1代表“一般犹豫”,π2代表“非常犹豫”。
定理1 六元语言真值直觉模糊格中,语言真值直觉模糊对的犹豫度如下:
1)没有犹豫的语言真值直觉模糊对有3个,即(A,J),(B,K)和(C,S);
2)一般犹豫的语言真值直觉模糊对有2个,即(B,J)和(C,K);
3)非常犹豫的语言真值直觉模糊对有1个,即(C,J)。
证明 根据定义4可证:设m∈LI6,
1)当m=(A,J)时,i=3且j=3,此时Π(m)=πk=π(3-3)=π0;
当m=(B,K)时,i=2且j=2,此时Π(m)=πk=π(2-2)=π0;
当m=(C,S)时,i=1且j=1,此时Π(m)=πk=π(1-1)=π0;
2)当m=(B,J)时,i=2且j=3,此时Π(m)=πk=π(3-2)= π1;
当m=(C,K)时,i=1且j=2,此时Π(m)=πk=π(2-1)=π1;
3)当m=(C,J)时,i=1且j=3,此时Π(m)=πk=π(3-1)=π2。
其中LI6上的语言真值直觉模糊犹豫度πk如图 2所示。
 |
| 图 2 六元语言真值直觉模糊犹豫度结构图Fig. 2 Structure diagram of six-element linguistic truth-valued intuitionistic fuzzy hesitate degree |
性质1 在语言真值直觉模糊格上(如图 1所示),语言真值直觉模糊对((hi,t),(hj,f))∈LI6的犹豫度πk有如下性质:
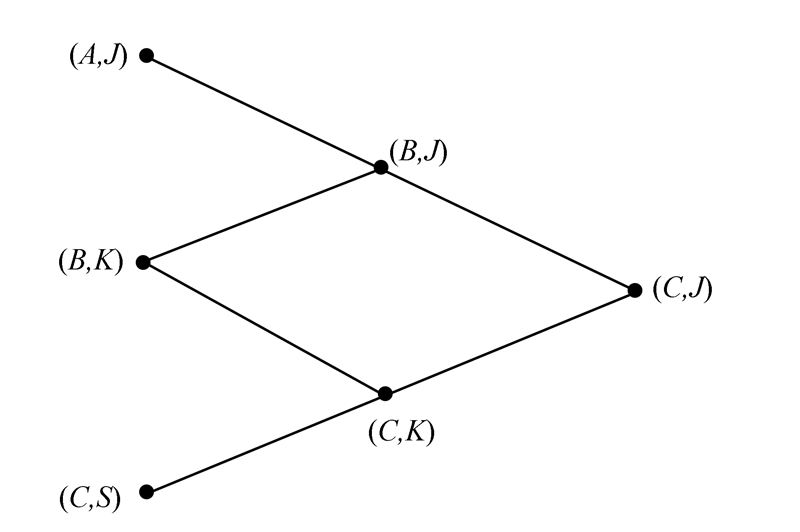 |
| 图 1 六元语言真值直觉模糊格的结构图Fig. 1 Structure diagram of six-element linguistic truth-valued intuitionistic fuzzy lattice |
1)当j不变时,随着i减小,πk增大;
2)当i不变时,随着j增大,πk增大。
证明 在六元语言真值直觉模糊格中,当j增大或减小时,πk相应的增大或减小,当i增大或减小时,πk相应的减小或增大,并且πk变化的范围与j或i变化的范围相一致。
定义5 在六元语言真值直觉模糊格中,规定Θ运算为(hi,cj) Θπk=(hmax(i,k),cj)且1≤i≤3,1≤j≤2,0≤k≤2。
定义6 设向量A=[a1a2…am],B=[b1b2…bn](ai,bi∈ LV(3×2),i=1,2,…,m,j=1,2,…,n)为语言真值直觉模糊集,则A与B 的语言真值直觉模糊关系定义为
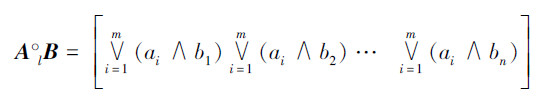
例1
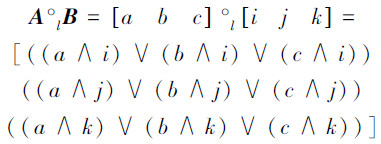
定义7 设A和A′ 均为语言真值直觉模糊集,对任意u∈LV(3×2),定义语言真值直觉模糊相容度为T(A/A′)(u),即A′ 在A限定下的相容程度,则

定义8 设A和A′ 均为语言真值直觉模糊集,对任意u∈LV(3×2),定义语言真值直觉模糊不相容度为S(A/A′)(u),即A′在A 限定下的不相容程度,则
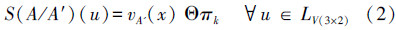
定义9 设B和B′ 均为语言真值直觉模糊集,由语言真值直觉模糊关系求出T(B/B′)和S(B/B′)的运算如下:
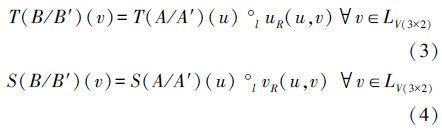
定义10 设B′ 为语言真值直觉模糊集,它是由T(B/B′)(v)、S(B/B′)(v)和B推导得出,运算如下:
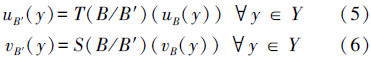
在经典逻辑中,常用三段论的形式来表示推理规则,描述形式简化如下:

基于上述表示形式,语言真值直觉模糊推理的描述形式简化如下:


语言真值直觉模糊推理的规则是[13]:先求出 A(uA,vA)→B(uB,vB)所表达的语言真值直觉模糊关系R6,然后再利用小前提A′(uA′,vA′),通过复合运算得出结论 B′(uB′,vB′)。
然而,真值限定的语言真值直觉模糊推理方法与语言真值直觉模糊推理方法相比,前者增加了一个新的属性参数,在推理过程中,前者不考虑已知规则的具体内容,而依据A( uA,vA)和A′(uA′, vA′)的相容度和不相容度,通过将其与R6进行运算,并将结果用B(uB,vB)来反限定推导出B′(uB′,vB′ )。这类似于在经典逻辑中,推理时不考虑命题的具体内容,而是依赖于命题的真值来进行推理。
3.2 真值限定的语言真值直觉模糊推理算法真值限定的语言真值直觉模糊推理算法的求解步骤如下:
1)将命题A(uA,vA),B(uB ,vB),A′(uA′,vA′ )进行简化,而后用向量表示出来;
2)用A(uA,vA)进行限定,分别计算A(uA,vA)与A′(uA′,v A′)的语言真值直觉模糊相容度T(A/A′)(u)和语言真值直觉模糊不相容度S(A/A′) (u);
3)选取六元语言真值直觉模糊蕴涵算子[13],把大前提A(uA,vA) →B(uB,vB)转化为一个X×Y上的六元语言真值直觉模糊关系R6:A(uA,vA) →B(uB,vB)。六元语言真值直觉模糊的蕴涵算子是:((hi,t),(hj,f)) →((hk,t),(hl,f))=((hmin(3,3- i+k,3-j+l),t),(hmin(3,3-i+l),f)) ;
4)分别将T(A/A′)(u)、S(A/A′)(u)与R6做运算,求出B(uB,vB)与B′(uB′,vB′)的语言真值直觉模糊相容度T(B/B′)(v)和语言真值直觉模糊不相容度S(B/B′)(v);
5)用B(uB,vB)反限定推导出B′(uB′,vB′)即 uB′(y)=T(B/B′)(uB(y)),vB′(y)=S(B/B′)(vB(y))。
真值限定的语言真值直觉模糊推理算法的推理过程如图 3所示。
 |
| 图 3 真值限定的语言真值直觉模糊推理过程Fig. 3 True value limit of linguistic truth-valued intuitionistic fuzzy reasoning process |
例2 人工调节淋浴水温,有如下的经验规则:如果水温低,则热水阀应开大,试问水温为“非常低”时,应怎么样调节热水阀?(这里不考虑冷水阀,认为其固定)
解 假定,取论域X与Y均为{1,2,3},分别表示水温和热水阀的3个等级。
设A表示X上的语言真值直觉模糊集“水温低”,则
A=(一般真,非常假)/1+(稍微真,非常假)/2+(稍微真,一般假)/3
设B表示Y上的语言真值直觉模糊集“开大热水阀”,则
B=(稍微真,稍微假)/1+(稍微真,非常假)/2+(一般真,非常假)/3
用IF-THEN规则表述题目中的经验就是:如果X是A,则Y是B。
以下分别取A′为“非常低”来计算对应的B′,对于“非常低”,取A′=(非常真,非常假)/1+(一般真,非常假)/2+(稍微真,稍微假)/3
用真值限定的语言真值直觉模糊推理方法解如下:
1) 将A,B,A′进行简化,然后用向量表示。
A=(B,J)(C,J)(C,K)
B=(C,S)(C,J)(B,J)
A′=(A,J)(B,J)(C,S)
2)计算相容度T(A/A′ )和不相容度S(A/A′)。
T(A/A′)(B)=uA′(1)Θπk=(h3,t)∨π0=(h3,t)=A
S(A/A′)(J)=vA′(1)Θπk=(h3,f)∨π0=(h3,f)=J
同理可得
故 T(A/A ′)(u)=A/B+B/C+C/C
S(A/A′)(u)=J/J+J/J+S/K
3) 由六元语言真值直觉模糊关系R6求出 B′在B限定下的语言真值。

4)用B反限定求B′。

同理
故 B′=(B,K)/1+(A,J)/2+(A,J)/3
即 B′=(一般真,一般假)/1+(非常真,非常假)/2+(非常真,非常假)/3
结果表明对应的B′为“热水阀开的非常大”。
4 结束语
本文提出的推理方法是将语言值作为证据信息进行处理,该方法更符合人类的语言表达,推理过程更贴近于人脑的思维过程,并且在处理可比性与不可比性信息时加入了犹豫度的计算,减少了推理过程中信息的损失。实例说明,真值限定的语言真值直觉模糊推理方法在处理可比性与不可比性问题时,更灵活、更有效。下一步的工作是将真值限定的语言真值直觉模糊推理方法应用于决策分析,风险评估等应用领域中。
| [1] | ZADEH L A. Fuzzy sets[J]. Information and Control, 1965, 8(3):338-353. |
| [2] | ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20(1):87-96. |
| [3] | ATANASSOV K T. More on intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1989, 33(1):37-45. |
| [4] | XU Yang, QIN Keyun, LIN Jun, et al. L-valued propositional logic Lvpl[J]. Information Sciences, 1999, 114(1-4):205-235. |
| [5] | 徐扬. 格蕴涵代数[J]. 西南交通大学学报, 1993(1):20-27.XU Yang. Lattice implication algebra[J]. Journal of Southwest Jiaotong University, 1993(1):20-27. |
| [6] | 夏佩伦. 不确定性推理方法研究[J]. 火力与指挥控制, 2010, 35(11):87-91. XIA Peilun. Comments on techniques for inference with uncertainty[J]. Fire Control & Command Control, 2010, 35(11):87-91. |
| [7] | 陈图云, 孟艳平. 模糊集相似度限定推理方法[J]. 工程数学学报, 2005, 22(2):346-348. CHEN Tuyun, MENG Yanping. The reasoning method by fuzzy set similarity degree[J]. Chinese Journal of Engineering Mathematics, 2005, 22(2):346-348. |
| [8] | 雷英杰, 王宝树, 路艳丽. 基于直觉模糊逻辑的近似推理方法[J]. 控制与决策, 2006, 21(3):305-310. LEI Yingjie, WANG Baoshu, LU Yanli. Approximate rea-soning method based on intuitionistic fuzzy logic[J]. Control and Decision, 2006, 21(3):305-310. |
| [9] | 雷英杰, 汪竞宇, 吉波, 等. 真值限定的直觉模糊推理方法[J]. 系统工程与电子技术, 2006, 28(2):234-236.LEI Yingjie, WANG Jingyu, JI Bo, et al. Technique for in-tuitionistic fuzzy reasoning with truth qualifications[J]. Sys-tems Engineering and Electronics, 2006, 28(2):234-236. |
| [10] | 王毅, 雷英杰. 基于直觉模糊逻辑的插值推理方法[J]. 系统工程与电子技术, 2008, 30(10):1944-1948. WANG Yi, LEI Yingjie. Techniques for interpolation rea-soning based on intuitional fuzzy logic[J]. Systems Engineering and Electronics, 2008, 30(10):1944-1948. |
| [11] | 赖家骏, 徐扬. 基于语言真值格值一阶逻辑的不确定性推理的语法[J]. 模糊系统与数学, 2011, 25(2):1-60. LAI Jiajun, XU Yang. Syntax of uncertainty reasoning based on linguistic truth-valued lattice value first-order logic[J]. Fuzzy Systems and Mathematics, 2011, 25(2):1-6. |
| [12] | 杨丽, 徐扬. 基于概念格的语言真值不确定性推理[J]. 计算机应用研究, 2009, 26(2):553-554, 576. YANG Li, XU Yang. Linguistic truth-valued uncertainty reasoning based on concept lattice[J]. Application Research of Computers, 2009, 26(2):553-554, 576. |
| [13] | 邹丽, 谭雪微, 张云霞. 语言真值直觉模糊逻辑的知识推理[J]. 计算机科学, 2014, 41(1):134-137. ZOU Li, TAN Xuewei, ZHANG Yunxia. Knowledge rea-soning based on linguistic truth-valued intuitionstic fuzzy logic[J]. Computer Science, 2014, 41(1):134-137. |
| [14] | 郑宏亮, 徐本强, 邹丽. 一种基于十元格蕴涵代数的知识表示方法[J]. 计算机应用与软件, 2013, 30(1):37-40. ZHANG Hongliang, XU Benqiang, ZOU Li. An approach for knowledge representation based on ten-element lattice implication algebra[J]. Computer Application and Sof-tware, 2013, 30(1):37-40. |
| [15] | 张云霞, 崔晓松, 邹丽. 一种基于十八元语言值模糊相似矩阵的聚类方法[J]. 山东大学学报, 2013, 43(1):1-7. ZHANG Yunxia, CUI Xiaosong, ZOU Li. A clustering method based on 18-element linguistic-valued fuzzy similar matrix[J]. Journal of Shandong University, 2013, 43(1):1-7. |
| [16] | 孙芳, 张凤梅, 邹丽, 等. 基于六元格值命题逻辑的语言真值归结方法[J]. 广西师范大学学报:自然科学版, 2010, 28(3):118-121.SUN Fang, ZHANG Fengmei, ZOU Li, et al. Linguistic truth-valued resolution method based on six-element lattice-valued propositional logic[J]. Journal of Guangxi Normal University:Natural Science Edition, 2010, 28(3):118-121. |
| [17] | 邹丽. 基于语言真值格蕴涵代数的格值命题逻辑及其归结自动推理研究[D]. 成都:西南交通大学, 2010:1-160. ZOU Li. Studies on lattice-valued propositional logic and its resolution-based automatic reasoning based on linguistic truth-valued lattice implication algebra[D]. Chengdu, China:Southwest Jiaotong University, 2010:1-160. |



