液压迈步式超前支护装备(以下简称“超前支护装备”)主要应用于综掘巷道的临时支护,能够有效保障巷道安全、高效、快速掘进[1]。随着开采的进行,围岩很容易发生大变形,甚至出现破裂、碎裂和整体失稳等严重现象[2, 3]。这就要求超前支护装备的支撑力具有充分的柔度以适应围岩应力动态变化,且能够有效减小迈步交替支撑时对顶板的扰动量[4]。近些年以来,模糊PID控制一直以其响应速度快、调节时间短、超调量和稳态误差小,适应能力极强的优点广泛应用于工业控制中[5]。2004年,蒋伟[6]首次提出了在电液伺服系统中应用模糊PID控制算法。2011年,史文萍[7]首次在液压支架控制中引入模糊PID控制算法,构成了性能稳定的系统,为液压支架的控制系统的设计提供了一条新的思路。本文结合前人的研究成果,首次将模糊PID控制算法应用于超前支护设备的支撑力控制中,对解决支撑力能够良好的适应围岩应力变化有着广泛的应用价值。
1 超前支护装备支撑力自动控制原理 1.1 超前支护装备工作原理及主要控制过程分析超前支护装备由机械系统、液压系统以及电控系统组成,其整机控制系统如图 1所示,各部分相互协调工作,完成超前支护的支撑作业任务[8, 9]。
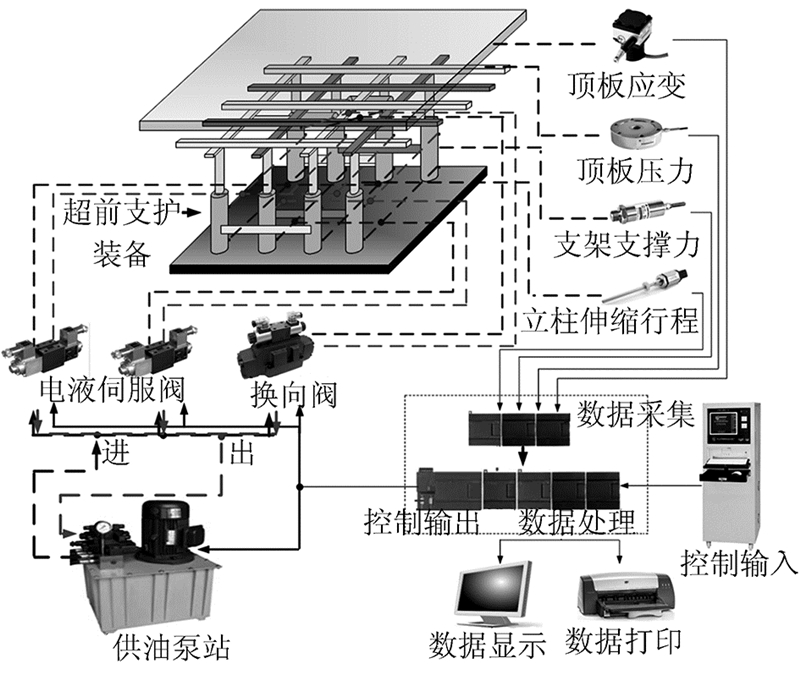 |
| 图 1 超前支护装备整机控制系统 Fig. 1 Control system of advance supporting equipment |
超前支护装备由主、副支撑构成。在掘进机截割时,超前支护两组共同支撑迎头顶板和侧帮。当开挖空顶距接近巷道许用空顶距时,超前支护采取单组支撑顶板,另一组下降卸载,由推移机构向前推移,实现迈步,然后上升加载,支撑顶板。接下来处于支撑状态那一组重复上述操作,实现交替迈步前行,直到超前支护接近截割头且不与之作业空间干涉为止。
超前支护装备的两组支撑立柱不论处于全支撑状态,还是处于单组支撑状态或者过渡过程,要实现超前支护向工作面移动,支撑立柱的支撑力必须发生变化,支撑力变化的显著时间区域发生在升架和降架2个过程,而这2个过程主要发生在超前支护装备处于过渡过程中。
为了保证综掘巷道在掘进时,超前支护对顶板的支护始终有效,并保持巷道顶板的稳定性,超前支护的控制系统必须对过渡过程的立柱支撑力进行有效控制,以保证过渡过程的稳定进行。因此,本文以非对称液压缸、电液伺服阀组成的整体作为被控对象,对超前支护过渡过程的支撑力控制进行研究。
1.2 支撑力自动控制原理超前支护装备支撑力自动控制原理如图 2。
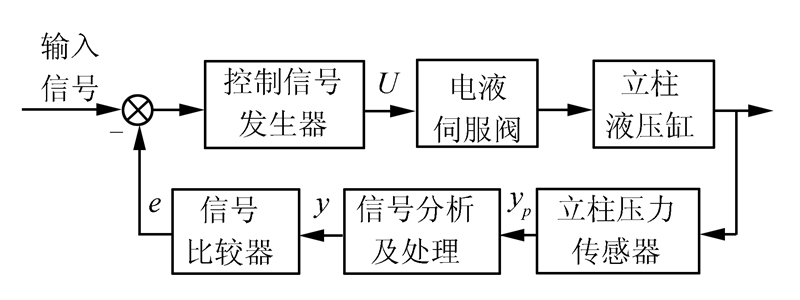 |
| 图 2 支撑力自动控制原理框图 Fig. 2 Automatic control principle diagram of supporting force |
在正常工作过程中,立柱压力传感器实时检测立柱支撑力大小,产生压力信号yp;信号经分析、滤波之后计算出所测压力的实际值y;实际值经信号比较器,与期望支撑力值进行比较,得出差值,并判断差值支撑力是否超过许用误差值,得出偏差信号e;控制信号发生器根据输入信号与偏差信号e的计算结果,产生电压信号U,控制电液伺服阀,使被控对象(液压缸)输出yp逼近期望支撑力值,也即使e→0。
在实际操作中,应用 MATLAB/SIMULINK 制作相应输入、输出模块及控制器,将传感器采集的力信号经模数转换,通过相应输入模块输入到工控机,在工控机中利用设计的控制器实现自动控制算法并将控制信号由相应的输出模块输出,经数模转换后将输出的信号转化为电压信号后反馈到电液伺服系统中,从而实现控制器对电液力伺服系统的控制。
2 控制对象的数学模型支撑油缸的精确控制是由控制电液伺服阀来实现,通过调整电液伺服阀控制电流的变化,从而调整其输出流量的大小,并最终控制支撑油缸活塞杆的移动速度。为了对支撑立柱在过渡过程中的降架和升架进行精确控制,需研究支撑油缸输出力的数学表达式,并通过数学表达式研究支撑油缸的控制方法问题。
为便于建立液压系统的数学模型和传递函数,对液压系统进行简化,如图 3所示,并做如下假设[8]:
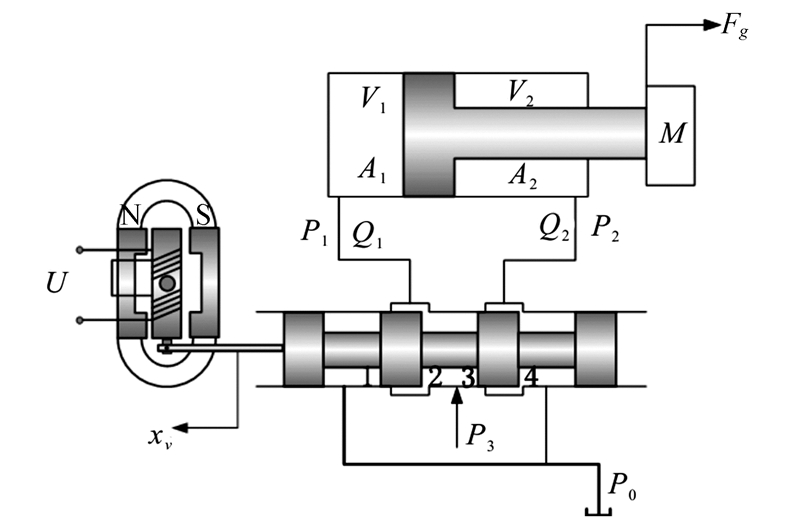 |
| 图 3 超前支护装备液压系统简化图 Fig. 3 Simplified diagram for the hydraulic system advanced supporting equipment |
1) 电液伺服阀为理想的零开口四通滑阀,且节流口为对称型,节流口处的液体流动为紊流,忽略阀内液体的压缩性;
2) 假设伺服阀具有理想的动态响应,即阀芯的位移、伺服阀进出口压力降和流量是瞬间发生;
3) 液压系统的供油压力ps恒定不变,回油压力p0为零,忽略液压管路、液体质量和管路动态特性的影响;
4) 液压缸每个工作腔内压力都相同,内外泄露认为是层流,油液温度和容积弹性模数设为常数。
图 3包括电液伺服阀、单作用液压缸、负载质量、负载弹性和阻尼系数。其中,负载质量是超前支护立柱和围岩直接顶的质量之和,弹性系数和阻尼系数是直接顶的固有模态。由3图可知,超前支护的控制系统将支撑油缸的控制信号送至电液伺服控制器,并经电液伺服控制器中的放大器将电信号送至伺服阀的先导阀,经先导阀的信号转换,将控制的电信号转换成阀芯移动的力。
在对非对称液压缸进行研究时,将非对称液压缸、电液伺服阀和负载看做一个整体,并认为负载具有弹塑性,想要得到控制对象的传递函数,必须先得出阀、液压缸的流量方程及液压缸的力平衡方程[11]。由于很多文献都详细叙述了上述3个方程的具体求导过程,本文不再详述,只给出以下方程结果:
1)阀的流量方程为
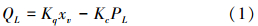
式中:Kq为流量增益,m2/s; Kc为流量压力系数,m3/(s·Pa);xv为阀芯位移,m;PL为负载压力,N。
2)液压缸的流量方程为
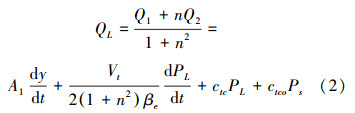
式中:Q1为液压缸无杆腔流量,m3/s;Q2为液压缸有杆腔流量,m3/s;n为有效面积比;A1为液压缸无杆腔面积,m2;βe为液压油液的等效弹性模数,N/m2;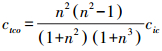 ,其中cic为液压缸的内泄露系数,m5·Ν/s;
,其中cic为液压缸的内泄露系数,m5·Ν/s;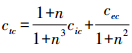 ,其中cic为液压缸的外泄露系数,m5·Ν/s。
,其中cic为液压缸的外泄露系数,m5·Ν/s。
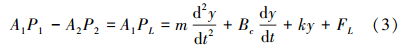
式中:A2为液压缸有杆腔面积,m2;m为等效质量之和,kg;Bc为活塞和负载的负载的粘性阻尼系数,N·s/m;k为负载的弹簧刚度,N/m;FL为等效外负载力,N。
对式(1)、(2)及(3)进行拉普拉斯变换,可得超前支护支撑油缸的力控制传递函数:
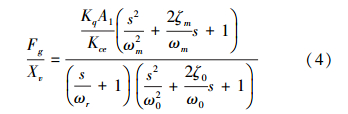
式中:Fg为作用在活塞上的任意外负载力,N;ωm为机械固有频率,Hz;ωr为转折频率,Hz,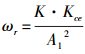 ;ω0为液压弹簧与机械弹簧构成的固有频率,Hz,
;ω0为液压弹簧与机械弹簧构成的固有频率,Hz,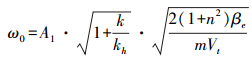 ;ζm为机械阻尼系数,N·s/m,
;ζm为机械阻尼系数,N·s/m,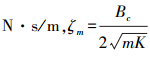 ;ζ0为液压与机械阻尼系数,N·s/m,
;ζ0为液压与机械阻尼系数,N·s/m,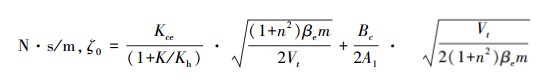 ;Kq/Kce为总的压力增益,Pa/m,
;Kq/Kce为总的压力增益,Pa/m,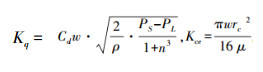 。
。
由于液压缸工作时,环境和负载会时时变化,且液压缸液压系统的本身具有非线性特性,控制系统的参数必然会发生波动,采用固定的PID参数去适应液压缸控制系统的全过程,其控制性能必然会受到影响。为了超前支护装备的支撑力(即液压缸的输出力)能够快速稳定地跟踪预期值,将模糊控制与传统PID结合,利用模糊推理的策略,根据不同的偏差、偏差变化率对PID的参数Δkp、Δki、Δkd进行在线自调整,使PID控制器能够适应控制的全过程[13]。
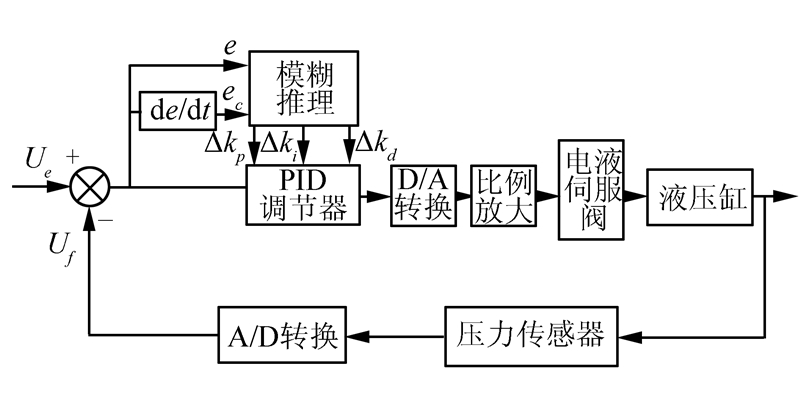 |
| 图 4 模糊PID支撑力自动控制系统结构图 Fig. 4 Structure graph of fuzzy-PID support force automatic control system |
设控制器的输入变量为e、ec,输出变量为Δkp、Δki、Δkd。输入与输出变量的模糊子集均定义为{NB,NS,ZO,PS,PB},同时,二者的隶属函数均采用三角形的隶属函数[12]。
根据PID 3个参数的作用及特性,制定Δkp、Δki、Δkd的模糊控制规则如表 1~表 3所示。
| e | Δkp | ||||
| ec= NB | ec= NS | ec= ZO | ec= PS | ec= PB | |
| NB | PB | PM | PM | PS | ZO |
| NS | PM | PM | NS | ZO | NS |
| ZO | PM | PS | ZO | NS | NB |
| PS | PS | ZO | NS | NB | NB |
| PB | ZO | NS | NB | NB | NB |
| e | Δkp | ||||
| ec= NB | ec= NS | ec= ZO | ec= PS | ec= PB | |
| NB | NB | NB | NS | NS | ZO |
| NS | NB | NS | NS | ZO | PS |
| ZO | NS | NS | ZO | PS | PS |
| PS | NS | ZO | PS | PS | PB |
| PB | ZO | PS | PS | PB | PB |
| e | Δkp | ||||
| ec= NB | ec= NS | ec= ZO | ec= PS | ec= PB | |
| NB | PS | NB | NB | NS | PS |
| NS | ZO | NS | NS | NS | ZO |
| ZO | ZO | NS | NS | NS | ZO |
| PS | ZO | ZO | ZO | ZO | ZO |
| PB | PB | PS | PS | PS | PB |
设定各个参数的量化等级:e、ec、Δkp、Δki、Δkd均等于{-6,-5,-4,3,-2,-1,0,1,3,4,5,6},考虑到实现模糊PID的控制器为PLC,而PLC的输入电压信号在0~10 V以内,根据系统实际工作状况,相应的输入输出变量的基本论域和模糊论域分别为e:[-10,10],ec:[-5,5],Δkp:[-3,3],Δki:[-3,3],Δkd:[-0.6,0.6];e∈[-5,5],ec∈[-5,5],Δkp∈[-1,1],Δki∈[-1,1],Δkd∈[-1,1][13, 14]。
则相应的量化因子分别为
ke=n/emax=0.5
kec=m/ecmax=1
kup=umax/l=3
kui=umax/l=0.3
kud=umax/l=0.6
式中:ke为误差量化因子;kec为误差变化量化因子;kup、kui、kud为比例因子;n为误差论域最大值;m为误差变化率论域最大值;emax为误差基本论域最大值;ecmax为误差变化率基本论域最大值;l为PID调节参数模糊论域最大值;umax为PID调节参数基本论域最大值。
定义参数Kp、Ki、Kd调整算式如下:
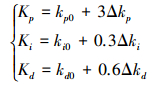
式中:Kp、Ki、Kd是模糊PID控制器的输出参数;kp0、ki0、kd0是PID控制器的初始值;Δkp、Δki、Δkd是在线运行过程中,根据e和ec,通过查询模糊控制规则表得到的调整量。
对于电液伺服阀和液压缸组成的被控对象而言,主要性能的参数有系统总增益K、固有频率ωm和阻尼系数ζm等。液压弹簧与机械弹簧构成的固有频率ω0的大小决定了电液伺服系统的响应速度,因此希望ω0尽可能大。影响ω0的因素主要有:液体的有效体积弹性模数βe、工作腔总容积Vt和液压缸工作面积A。根据相关规则及公式,选择系统的重要参数如表 4所示[11]。
| 参数 | 数值 | 参数 | 数值 | |
| A1/m2 | 3.1×10-3 | cd | 0.62 | |
| w/m | 0.023 7 | ρ/(kg· m3) | 850 | |
| n | 0.5 | β e/Pa | 7×10 8 | |
| P s/Pa | 16×10 6 | B c/(N·s·m -1) | 800 | |
| F L/N | 3 000 | K/(N·m-1) | 40 000 | |
| V/m 3 | 0.1×10 -3 | c ic/(m 3·s -1·Pa -1) | 4×10 -11 | |
| P 0/Pa | 0 | c ec/(m 3·s -1·Pa -1) | 0 | |
| A 2/m 2 | 1.5×10 -3 | m/kg | 40 |
由表 4中参数可得超前支护支撑油缸的力控制传递函数:
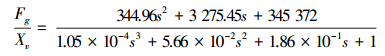
由此,利用MATLAB中Simulink模块的模糊逻辑工具箱和控制系统工具箱建立仿真系统模型,如图 5所示[15]。输入幅值为1的阶跃信号,信号从0时刻开始输入,采样时间设为1 s。常规PID和模糊PID控制的正弦信号响应和阶跃信号响应仿真曲线比较如图 6~7所示。
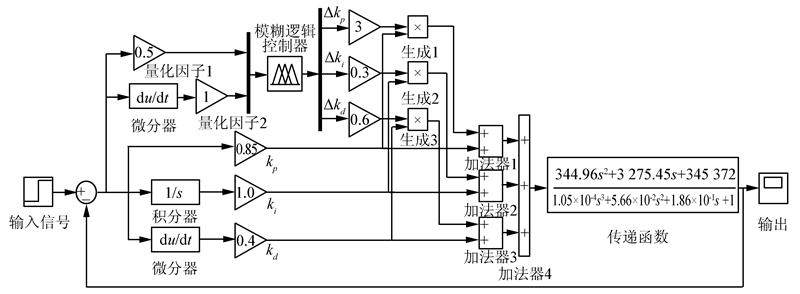 |
| 图 5 仿真模型 Fig. 5 Simulation model |
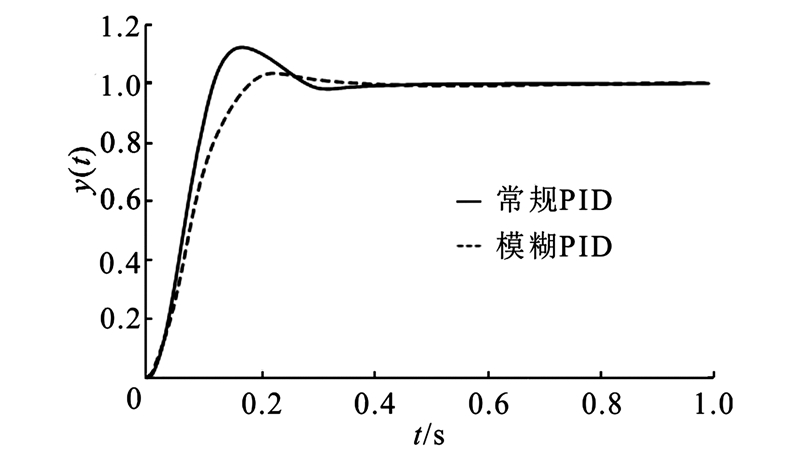 |
| 图 6 阶跃信号响应仿真曲线 Fig. 6 Step signal response curves |
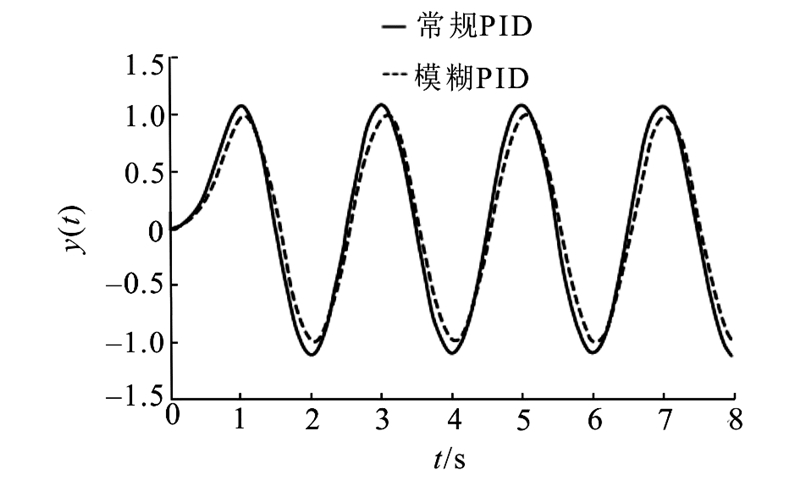 |
| 图 7 正弦信号响应仿真曲线 Fig. 7 Sine signal response curves |
模糊PID控制比常规PID控制具有更小的超调量,而且能够较快地达到稳定,其控制效果优于常规PID控制。
4 实验研究 4.1 超前支护装备模拟实验平台的组成超前支护装备模拟实验平台主要由3大部分组成:迎头顶板模拟实验框架、超前支护实验样机和测量基准框架,如图 8所示。
 |
| 图 8 模拟实验平台实物 Fig. 8 Experimental platform for the simulation |
1)迎头顶板模拟实验框架可通过调节框架顶部加载液压缸组的油压值,对模拟顶板进行不同载荷的工况模拟。迎头顶板模拟实验框架的加载液压伺服系统可以实现静力学加载曲线压力值保压调控,也可以实现按照多种激励作用下的动力学加载曲线压力变化规律对模拟顶板进行加载实验。
2)实验样机具有双组支撑、单组支撑、交替支撑以及液压迈步移动功能;利用双组交替支撑结构使超前支护在交替移动时,模拟巷道顶板始终存在有效支撑,并且保证顶板受力基本保持稳定。样机上安装有位移、压力、油压等传感器和电控装置。
3)测量基准框架不受实验加载力和框架设备变形影响,为实现系统的不同测量面提供相对地面的水平和垂直测量基准点。
4.2 过渡状态下支撑力自动控制实验实验过程中,由模拟顶板进行模拟顶板工况加载,超前支护样机完成一个完整的迈步过程,由计算机截取过渡态动作28 s为测试时间,然后利用数据采集设备,实时采集安装在超前支护样机两组立柱上的压力传感器的数值,以此来监测支撑力的变化状况。
通过实验得到超前支护实验样机处在过渡态时各组立柱支撑力的数据,将数据处理绘制成图 9~10。
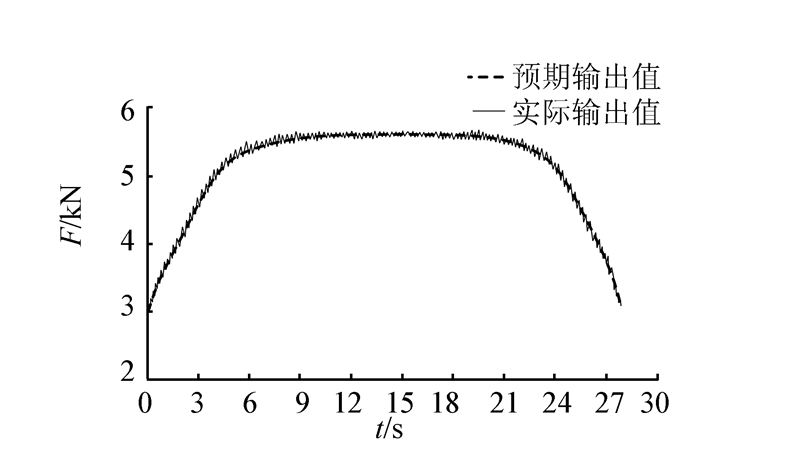 |
| 图 9 固定支撑组立柱支撑力变化曲线 Fig. 9 Fixed support column support force curve |
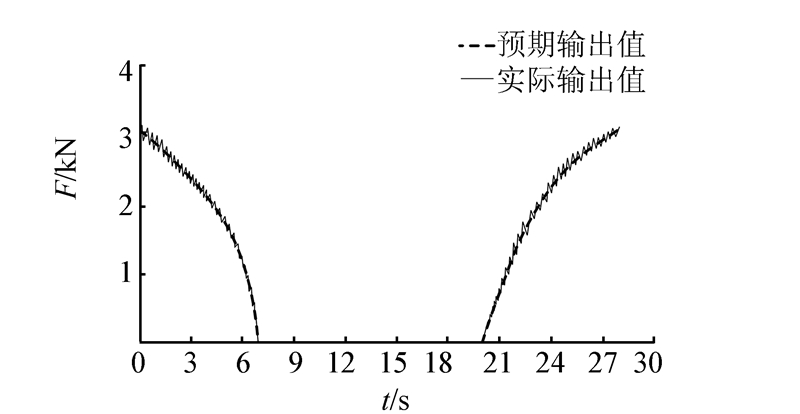 |
| 图 10 迈步组立柱支撑力变化曲线 Fig. 10 Move column support force curve |
从2组立柱支撑力的实验数据可以看出,在为期28 s的过渡过程中,2组立柱的支撑力均围绕预期值小范围波动,波动频率高(即支撑力自动调整时间快),变化趋势能够紧密跟随支撑力预期值的变化,其中:
1)固定支撑组立柱的支撑力出现较大波动发生在5~7 s时间段内,因为在此时间段内,迈步组立柱逐渐完全脱离顶板,超前支护装备由双组支撑变为单组支撑,固定支撑组立柱受顶板负载及其他振动影响较大,支撑力与预期值最大误差为117.3 N;在其他时间段支撑力与预期值呈波动平衡态,最小误差13.5 N。
2)由于迈步支撑组立柱执行“卸载—迈步—加载”的过程,支撑力的较大波动的出现在立柱刚刚开始脱离顶板和即将完全支撑顶板2个阶段,即图中0~1.5 s和26~28 s 2个时间段,在这2个阶段中立柱受顶板负载影响较大,与预期值最大误差为102.7 N ;在其他时间段,支撑力与预期值呈波动平衡态,最小误差为11.3 N。
所以,从实验结果来看,基于模糊PID的支撑力自动控制系统可以很好地对超前支护装备支撑力进行自动控制,被控系统的动态响应速度和超调量得到了较好的控制,系统的动静态性能、抗干扰能力及对参数的时变鲁棒性均得到较大的提高。
5 结束语1)分析了超前支护装备支撑力的自动控制原理并设计了一种智能模糊PID控制器。通过利用MATLAB/Simulink仿真分析可知,模糊PID控制较常规PID控制具有更加优越的性能,超调量小,响应时间快。
2)通过在超前支护装备模拟实验平台上进行的模拟实验研究,证明本文基于模糊PID的支撑力控制系统可以很好地应用在超前支护装备上,响应速度快,稳定,抗干扰能力强,能够对超前支护装备的支撑力进行良好地自动控制。
| [1] | 齐占波, 王宇, 王士伟. 煤矿巷道掘进成套设备及施工工艺研究[J]. 煤炭技术, 2010, 29(9): 60-62.QI Zhanbo, WANG Yu, WANG Shiwei. Research on coal-mining laneway excavating whole sets and constructing techniques[J]. Coal Technology, 2010, 29(9): 60-62. |
| [2] | JACOBI O. Testing the suitability of face roof Supports—Duty of the research institute for mine supports and rock mechanics[J].Bergbau and Energie, 1974, 110(5): 159-164. |
| [3] | 叶明亮. 采场顶板破断规律及其应力状态的研究[J]. 贵州工业大学学报, 1998, 27(3): 13-22. YE Mingliang. Study of the rupture pattern and stress of the roof rock in aworkplace[J]. Journal of Guizhou University of Technology, 1998, 27(3): 13-22. |
| [4] | 鹿志发. 浅埋深煤层顶板力学结构与支架适应性研究[D]. 北京: 煤炭科学研究总院, 2007: 16-22.LU Zhifa. Study on strata mechanical structure and support adaptability of shallow seam[D]. Beijing: Coal Science Research Institute, 2007: 16-22. |
| [5] | SPOONER J T, PASSION K M. Stable adaptive control using fuzzy systems and neutral networks[J]. IEEE Trans Fuzzy Systems, 1996, 4(3): 339-359. |
| [6] | 蒋伟. 模糊自适应PID控制算法在电液伺服系统中的应用[D]. 南京: 南京理工大学, 2004: 3-9.JIANG Wei. Application of fuzzy adaptive PID control algorithm in electro hydraulic servo system[D]. Nanjing, China: Nanjing University of Science and Technology, 2004: 3-9. |
| [7] | 史文萍. 基于模糊自适应PID控制在液压支架监控中的应用[J]. 煤矿机械, 2011, 32(1): 196-197.SHI Wenping. Application of controlling system for hydraulic support based on fuzzy adaptive PID control[J]. Coal Mine Machinery, 2011, 32(11): 196-197. |
| [8] | 王永安. 综放面端头自移式超前支护液压支架的设计研究[D]. 青岛: 山东科技大学, 2005: 6-10.WANG Yongan. Design and research of the automatic advanced hydraulic bracket in compositive area[D]. Qingdao: Shandong University of Science and Technology, 2005: 6-10. |
| [9] | 王士伟,王宇,赵成雷,等.掘进机机载临时支护机的设计与研究[J].煤矿机械,2011,32(6):52-53.WANG Shiwei, WANG Yu, ZHAO Chenglei, et al. Design and research of the temporary support machine for the boring machine[J]. Coat Mine Machinery, 2011,32(6):52-53. |
| [10] | 任金萍. 巷道用自移式辅助支护设备的结构研究[D]. 阜新: 辽宁工程技术大学, 2009: 3-9.REN Jinping. The research of the structure of self-motion assistanced powered support equipment for roadway[D]. Fuxin, China: Liaoning Technical University, 2009: 3-9. |
| [11] | 张立春. 自适应控制器及其在阀控非对称缸力系统中的应用[D]. 哈尔滨: 哈尔滨工业大学, 2006: 17-26.ZHANG Lichun. Adaptive controller and its application in the force system of asymmetrical cylinder controller by symmetric valve[D]. Harbin: Harbin Institute of Technology, 2009: 17-26. |
| [12] | PARNICHKUN M, NGAECHAROENKUL C. Kinematics control of a pneumatic system by hybrid fuzzy PID[J]. Mechatronics, 2001, 11(8): 1001-1023. |
| [13] | 陈斌, 史艳红, 邢志伟. 模糊PID控制在液压缸力控制中的应用[J]. 自动化技术与应用, 2007, 26(6): 27-29.CHEN Bin, SHI Yanhong, XING Zhiwei. Fuzzy PID control in the force control of hydraulic cylinder[J]. Techniques of Automation and Application, 2007, 26(6): 27-29. |
| [14] | 曹春平, 孙宇. 液压机压边力模糊PID智能控制系统研究[J]. 中国机械工程, 2010, 21(21): 2551-2554.CAO Chunping, SUN Yu. Study on fuzzy PID intelligent control system for hydraulic press blank-holder force[J]. China Mechanical Engineering, 2010, 21(21): 2551-2554. |
| [15] | 刘金棍. 先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2006: 55-67. |



