2. 江苏省大气环境与装备技术协同创新中心, 江苏 南京 210044
2. Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technol-ogy(CICAEET), Nanjing 210044, China
盲均衡算法是一种不需要发射训练序列,而仅依靠自身接收序列的统计特性调整均衡器权向量,使得输出序列接近于发送序列的自适应算法。其中,常模盲均衡算法(constant modulus algorithm,CMA)具有复杂度低、稳定性好和实时性强等优点。然而,其收敛速度慢、易局部收敛和难以均衡高阶多模QAM(quadrature amplitude modulation)信号。而多模盲均衡算法(multi-modulus algorithm,MMA)不仅具备CMA的优点,还可以有效均衡高阶多模QAM信号,并能进一步减小稳态误差、降低复杂度、加快收敛速度、纠正相位旋转[1]等,但仍存在局部收敛和误收敛。
蝙蝠算法(bat algorithm,BA)是一种基于种群的随机全局寻优算法,搜索空间中的每只蝙蝠都是寻优过程中的一个解,且对应着一个目标函数值,每只蝙蝠通过改变频率、发射脉冲频度和响度,以跟随当前最优的蝙蝠继续搜索。BA除具有其他智能算法的主要优点,还具有回波定位的特性,收敛速度快、寻优精度高[2, 3, 4]。
本文充分利用BA和MMA的优点,将2者有机结合起来,提出了一种基于双蝙蝠群智能优化的多模盲均衡算法(multi-modulus blind equalization algorithm based on double bat swarms intelligent optimization,MMBA-DBSIO),并通过仿真验证该算法的可行性。
1 多模盲均衡算法传统的MMA结构如图 1实线框部分所示[5, 6, 7]。图 1中,a(k)是零均值独立同分布的发射信号;c(k)是信道脉冲响应,等价于横向滤波器;n(k)是加性高斯白噪声(additive white Gaussian noise,AWGN);y(k)是盲均衡器的输入信号,yR(k)是y(k)的实部,yI(k)是y(k)的虚部;wR(k)是盲均衡器权向量w(k)的实部,wI(k)是w(k)的虚部;z(k)是盲均衡器的输出信号;zR(k)是z(k)的实部,zI(k)是z(k)的虚部;eR(k)是误差函数e(k)的实部,eI(k)是e(k)的虚部。
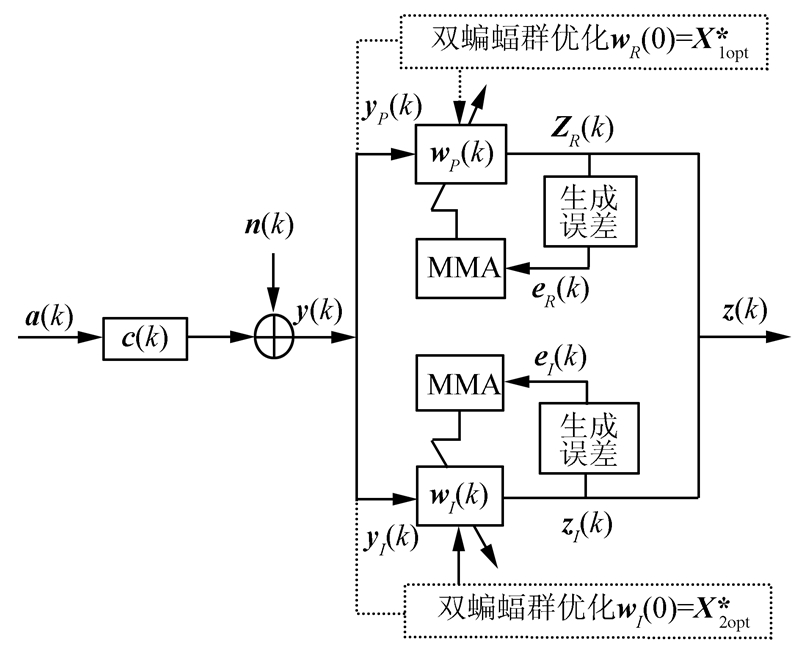 |
| 图 1 MMA原理图 Fig. 1 Schematic diagram for MMA |
由图 1可得如下关系:
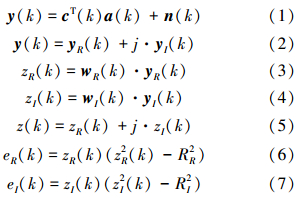
式中:RR2和RI2分别为发射信号实部和虚部的统计模值[8],分别定义为
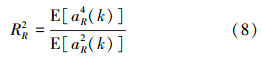
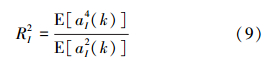
CMA对常模信号具有很好的均衡效果,但由于常模信号只有一个模值,收敛后,所有信号星座点均收敛于一个半径为模值R的圆上。而高阶多模QAM(如4阶以上)信号有多个模值,信号星座点是分布在半径为不同模值的圆上,采用CMA均衡高阶多模QAM信号时,将分布在不同半径圆上的信号星座点收敛到同一个圆上,从而导致均衡失效。而MMA在均衡高阶多模QAM信号时,将信号星座点均衡到不同模值对应的不同圆上,可以更有效地均衡多模信号[1]。以64QAM信号为例,其星座图如图 2所示。
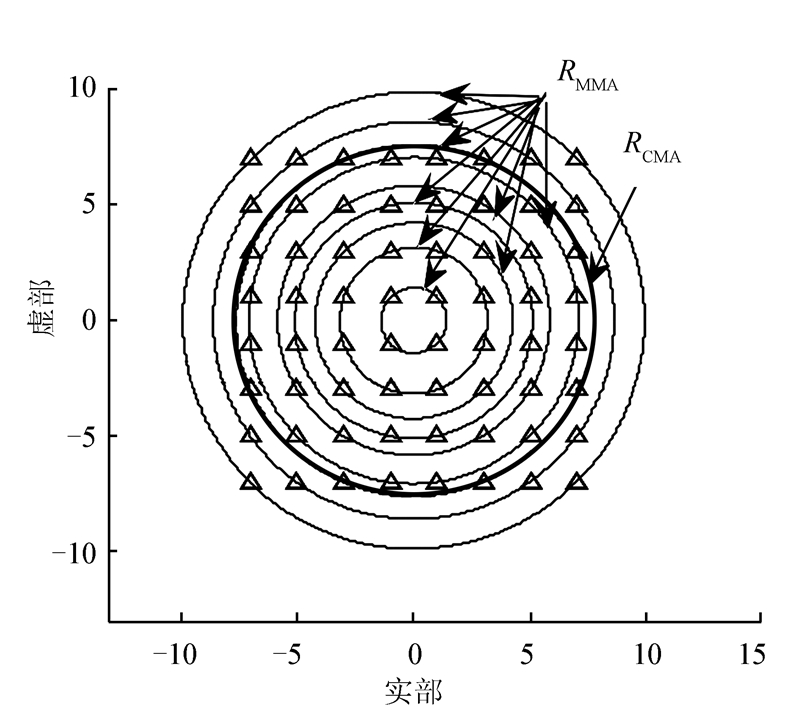 |
| 图 2 64QAM信号的模值 Fig. 2 Module values for 64QAM signal |
图 2中,信号点分别位于模值RMMA对应的9个圆上,RCMA为64QAM信号的一个等价固定模值(图中粗虚线圆,与MMA中一个模值对应的圆重合)[9]。图 1所示的MMA是将输入信号y(k)分成实部yR(k)与虚部yI(k)先分别均衡,均衡之后再合并的MMA。
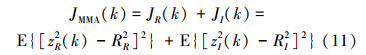
按照最速下降法,得
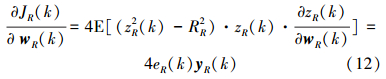
同理,得

所以,MMA权向量w(k)的实部和虚部迭代公式分别为
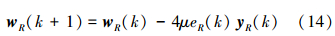
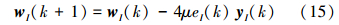
MMA具有可靠的初始收敛能力和载波恢复能力等优点,还具有纠正星座相位旋转的能力;但也存在收敛速度慢、局部收敛、收敛后稳态误差大的缺陷。
2 双蝙蝠群智能优化多模盲均衡算法 2.1 蝙蝠算法在一个d维搜索空间中,第i只蝙蝠的速度和位置更新公式[11, 12, 13, 14, 15]为
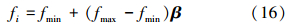
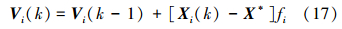
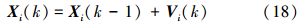
式中:Vi(k)为蝙蝠个体i在k时刻的速度;Xi(k)为蝙蝠个体i在k时刻的位置;β∈[0,1]是一个随机向量;X*是当前全局最优位置;fi为蝙蝠个体i在搜索猎物时的脉冲频率,其范围[fmin,fmax],频率越高,波长越小,传播的距离也越短,蝙蝠超声波的典型波长一般是几米,其取值范围由实验过程确定。
局部搜索时,一旦从至当前时刻k为止的各蝙蝠个体的最优位置向量中选出一个位置向量Xold,那么所有蝙蝠的新位置向量Xnew就在位置向量Xold附近随机游走产生[2, 3, 11, 12, 13, 14, 15],更新公式为
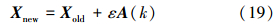
式中:ε为[-1,1]上的随机数,A(k)为蝙蝠群体在k时刻的平均响度。用Xnew替代原来的位置向量Xi(k),并继续搜索猎物。
蝙蝠速度和位置的更新与粒子群算法(particle swarm optimization,PSO)有些类似,频率fI控制了粒子移动的速度和范围。一定程度上,BA可以看作是标准PSO和由响度与频度控制的局部搜索的有机结合。
回波定位应用于蝙蝠的局部搜索过程。蝙蝠在搜索猎物时,起初发出的超声波响度A(0)大而频度r低,以便在更广的空间搜索猎物;发现猎物后,超声波的响度A减小、频度r增大,以便更精确地搜索猎物。响度A的取值范围[Amin,Amax]可以是任意的,其A(0)=Amax表示最大响度,Amin表示最小响度。响度A的大小也表示蝙蝠距离猎物的远近,响度A越接近Amin,说明蝙蝠距离猎物越近。当A=Amin=0时,说明蝙蝠刚好捕获猎物,暂时不再发出超声波[10, 11]。因此,超声波的响度和频度的更新公式可写为

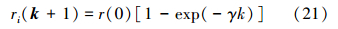
式中:Ai(k)为蝙蝠个体i在k时刻的响度;α为响度衰减系数;r(0)为最大频度;ri(k+1)为蝙蝠个体i在k+1时刻的频度;γ为频度增加系数,是大于零的常数。
对于任意的0 < α < 1和γ > 0,当k→∞时, Ai(k)→0,ri(k)→r(0)。初始化过程中,每只蝙蝠应该有不同的响度和频度,通常A(0)∈[1,2],r(0)∈[0,1]。当最优位置改变时,响度和频度也同时进行更新,表示所有蝙蝠朝着最优位置移动,具体参数值由实验过程确定。 2.2 双蝙蝠群目标函数BA除具备类似粒子群算法的记忆特性、遗传算法的交叉、突变特性外,自身还具有回波定位这一特性。回波定位主要应用于蝙蝠的局部搜索过程,通过对局部最优位置进行随机扰动,避免搜索过程陷入局部最优。蝙蝠算法的诸多特性极大地加快了收敛速度,提高了寻优精度。而MMA的收敛速度慢、收敛后稳态误差大,BA收敛速度快、寻优精度高的特点恰好可以弥补MMA的缺陷。
将BA引入到MMA中,利用蝙蝠的超声波探测、定位、捕食等行为,将蝙蝠离猎物距离的远近作为衡量蝙蝠个体所处位置好坏的标准。蝙蝠离猎物越近,捕获猎物的概率越大,所处位置越好,对应位置的目标函数值也越小。蝙蝠搜索猎物和移动过程类比为用好位置代替差位置的过程,从而获取全局最优位置,即全局最优解。
MMA将均衡器输入信号y(k)分成实部yR(k)与虚部yI(k)2部分处理,为获得最佳的均衡效果,这里利用2个不同的蝙蝠群体独立寻优,获得2个全局最优位置向量X1opt*和X2opt*,分别作为MMA的初始化权向量w(0)的实部wR(0)和虚部wI(0),再对wR(k)和wI(k)进行更新,以实现对yR(k)和yI(k)的分别均衡。
这就是本文提出的DBSIO-MMA,弥补了MMA收敛速度慢、收敛后稳态误差大等缺陷;与单蝙蝠群优化的多模盲均衡算法相比,DBSIO-MMA利用2个不同的蝙蝠群体独立寻优,获得2个不同的全局最优位置向量,避免了把同一全局最优位置向量同时作为最优初始权向量的实虚部进行均衡带来的偶然性,使算法更稳定。
用MMA的代价函数定义双蝙蝠群算法(double bat algorithm,DBA)的目标函数,用于计算目标函数值。现定义双蝙蝠群目标函数。
蝙蝠种群1第i个个体的目标函数定义为
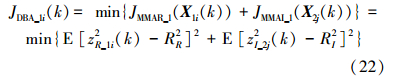
式中

对于种群1中第i个个体,j取遍种群2所有个体,X1i(k)为蝙蝠种群1第i个个体的位置向量,X2j(k)蝙蝠种群2第j个个体的位置向量;X1i(k)与X2j(k)分别作为初始优化过程中MMA初始权向量w(0)的实部wR(0)和虚部wI(0)。
蝙蝠种群2第j个个体的目标函数为
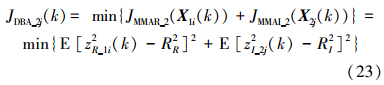
对于种群2中第j个个体,i取遍种群1中所有个体。
当代最优解:
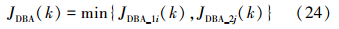
根据式(22)~(24),对MMA的初始权向量进行优化,步骤如下:
1) 初始化算法参数。随机产生蝙蝠种群1和种群2,每个蝙蝠群中蝙蝠数量均为n,频率范围均为[fmin,fmax],种群1最大响度为A1(0),种群2最大响度为A2(0),种群1最大频度为r1(0),种群2最大频度为r2(0),搜索精度均为tol,维数均为d,响度衰减系数均为α,频度增加系数均为γ,最大迭代次数均为iter,运行次数均为runs,信道为c,信噪比均SNR,实部与虚部权向量抽头个数均为L,蝙蝠种群1中第i只蝙蝠个体的位置向量为X1i,蝙蝠种群2中第j只蝙蝠个体的位置向量为X2j。
2) 计算目标函数值。按照式(22)~(24)分别计算目标函数值并比较其大小。当目标函数值最小时,选取对应的2个蝙蝠个体的位置向量为当前全局最佳位置向量X1*和X2*。
3)调整种群1的脉冲频率f1i和种群2的脉冲频率f2j,利用式(17)、(18)分别对2个种群中每个蝙蝠个体的速度和位置进行更新,得到种群1的X1i(k)和种群2的X2j(k)。
4)产生一个随机频度rand1,并与种群1中第i只蝙蝠的频度r1i进行比较,若rand1>r1i,对种群1中处于当前最优位置的蝙蝠个体随机扰动产生一个新的位置,替代种群1中第i只蝙蝠的当前位置并继续搜索猎物。同理,产生一个随机频度rand2,并与种群2中第j只蝙蝠的频度r2j进行比较,若rand2 > r2j,对种群2中处于全局最优位置的蝙蝠个体随机扰动产生一个新的位置,替代种群2中第j只蝙蝠的当前位置并继续搜索猎物。
5) 产生一个随机响度rand3,并与种群1中第i只蝙蝠的响度A1i进行比较,若rand3 < A1i且JDBA_1i(X1i(k)) < JDBA_1i(X1*),则用种群1中蝙蝠个体i的当前位置向量X1i及与X1i对应的种群2中蝙蝠个体j的当前位置向量X2j分别替代当前最优位置向量X1*和X2*,并利用式(20)、(21)对A1i、r1i进行更新。同理,产生一个随机响度rand4,并与种群2中第j只蝙蝠的响度A2j进行比较,若rand < A2j且JDBA_2j(X2j(k)) < JDBA_2j(X2*),则用种群2中蝙蝠个体的当前位置向量X2j及与X2j对应的种群1中蝙蝠个体i的当前位置向量X1i分别替代当前最优位置向量X2*和X1*,并利用式(20)、(21)对A2j、r2j进行更新。
6)根据式(24),选取当前全局最佳位置向量X1*和X2*。
7) 达到最大迭代次数或搜索精度,则分别输出2个种群的全局最佳位置向量,并记作X1opt*和X2opt*,否则转至3)。
8)将全局最佳位置X1opt*和X2opt*分别作为盲均衡器的最优初始权向量的实部和虚部,即wR(0)=X1opt*,wI(0)=X2opt*,再利用式(14)与式(15)分别对wR(k)与wI(k)进行更新,就可对y(k)进行有效均衡。
以基于两蝙蝠群体独立优化获得各自全局最优位置向量,并作为多模盲均衡算法的初始优化权向量,由此算法到了DBSIO-MMA。
3 仿真分析为了验证DBSIO-MMA的性能,以CMA、MMA、PSO-MMA和BA-MMA为比较对象,进行仿真实验。
参数初始化:对于CMA、MMA、PSO-MMA、BA-MMA和DBSIO-MMA,最大迭代次数均为iter=2 000,运行次数均为runs=2 000,信道均为
c=[0.955 6 -0.090 6 0.057 8 0.236 8]
信噪比均为SNR=25,均衡器抽头个数均为L=11;对于DBSIO-MMA,每个蝙蝠种群数中蝙蝠个体的数量n1=20,频率范围[0,100],种群1最大响度A1(0)=1.5,种群2最大响度A2(0)=1.5,种群1最大频度r1(0)=0.25,种群2最大频度r2(0)=0.25,搜索精度tol=10-5,响度衰减系数α=0.9,频度增加系数γ=0.9;BA-MMA参数设置为DBSIO-MMA种群1;对于PSO-MMA,学习因子c1=c2=1.494 45,最大粒子速度Vmax=1,粒子数n2=20,惯性因子wstart=0.9和wend=0.45(调节搜索范围)。
以16QAM为发射信号,分别以μCMA=μMMA=0.025、 μPSO-MMA=μBA-MMA=μDBA-MMA=0.005为步长,仿真结果如图 3所示。
 |
| 图 3 16QAM信号仿真结果 Fig. 3 Simulation results for 16QAM signal |
图 3表明,与CMA和MMA需迭代600次才达到收敛状态相比,PSO-MMA、BA-MMA和DBSIO-MMA均只需迭代30次左右即达到收敛状态,收敛速度得到极大地提高;收敛后DBSIO-MMA的均方误差达到-23 dB,比CMA降低了8 dB,比MMA降低了5 dB,比PSO-MMA降低了3 dB,比BA-MMA降低了1.8 dB;DBSIO-MMA的输出星座最清晰、最紧凑,均衡效果最好。
以64QAM为发射信号,分别以μCMA=μMMA=0.012、 μPSO-MMA=μBA-MMA=μDBA-MMA=0.003 8为步长,仿真结果如图 4所示。
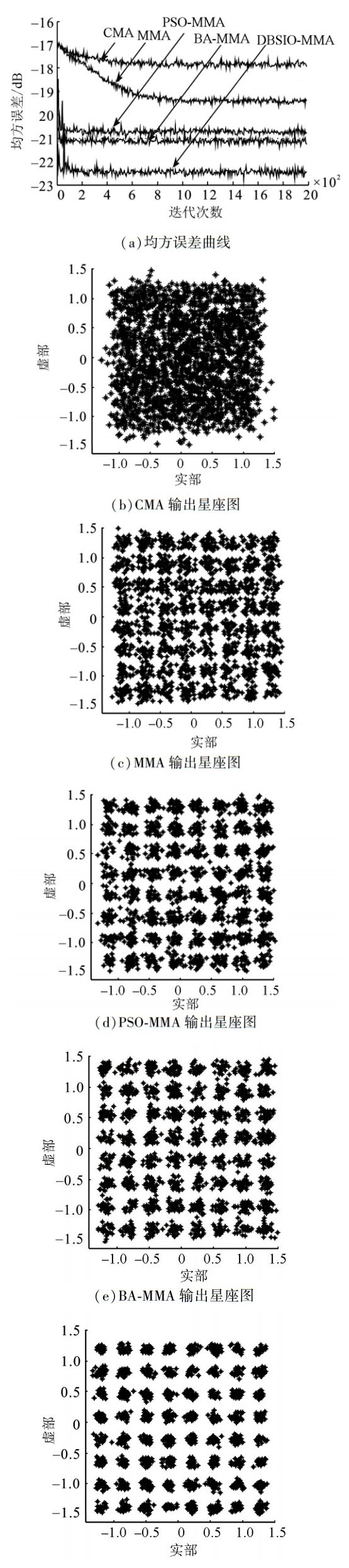 |
| 图 4 64QAM信号仿真结果 Fig. 4 Simulation results for 64QAM signal |
图 4表明,与CMA和MMA需迭代1 000次左右才达到收敛状态相比,PSO-MMA、BA-MMA和DBSIO-MMA均只需迭代80次左右即达到收敛状态,收敛速度得到极大地提高;收敛后DBSIO-MMA的均方误差达到-22.5 dB,比CMA降低了4.5 dB,比MMA降低了3 dB,比PSO-MMA降低了2 dB,比BA-MMA降低了1.5 dB;DBSIO-MMA的输出星座最清晰、最紧凑,均衡效果最好。
上述实验表明,与采用中心抽头初始化权向量的CMA与MMA及采用PSO优化初始权向量的MMA相比,采用由蝙蝠群优化初始权向量的MMA获得了最快收敛速度、最小均方误差、最清晰输出星座图,均衡高阶多模QAM信号的性能最好,主要是由于BA在一定程度上可以视为标准PSO和由响度与频度控制的局部搜索的有机结合,其中的回波定位功能在于局部搜索过程中起着其它智能算法无法获得效果,当搜索过程陷入局部最优时,通过回波定位功能对局部最优位置进行随机扰动,产生新的位置向量,以跳出局部搜索,回到全局搜索。因此,BA更易得到全局最优解,均衡效果也更好;而采用DBA寻优的过程,进一步加快了利用回波定位功能在跳出局部搜索的速度,从而加快了整个算法的收敛速度,同时减小了均方误差,获得了进一步提升的均衡效果。
4 结束语本文将BA与MMA有机结合,并采用2个种群独立寻优,提出了DBSIO-MMA。理论分析与仿真结果表明,该算法弥补了CMA、MMA难以均衡高阶QAM信号的缺陷。此外,该算法还有效地加快了收敛速度、减小了均方误差、纠正了相位旋转。因此,DBSIO-MMA是切实可行的。本文提出的算法在处理128阶或更高阶的信号时存在一定的局限性,在今后的工作中将进一步优化该算法,如引入正交小波变换等,以获得更优的均衡效果。该算法可以引入到信道模拟器硬件系统中,用以均衡高阶调制信号。因此,如何将该算法移植到硬件系统中,也是未来的研究方向之一。
| [1] | WEN Siyuan, LIU Feng. A computationally efficient multi-modulus blind equalization algorithm[C]// 2nd IEEE International Conference on Information Management and Engineering (ICIME). Chengdu, China, 2010: 685-687. |
| [2] | 李煜, 马良. 新型全局优化蝙蝠算法[J]. 计算机科学, 2013, 40(9): 225-229.LI Yu, MA Liang. Bat-inspired algorithm: a novel approach for global optimization[J]. Computer Science, 2013, 40(9): 225-229. |
| [3] | 刘长平, 叶长春, 刘满成. 来自大自然的寻优策略: 像蝙蝠一样感知[J]. 计算机应用研究, 2013, 30(5): 1320-1322.LIU Changping, YE Changchun, LIU Manchang. Optimization strategy from nature: perceive as bat[J]. Application Research of Computer, 2013, 30(5): 1320-1322. |
| [4] | PARACHA K, ZERGUIN A. A Newton-like algorithm for adaptive multi-modulus blind equalization[C]//International Workshop on Systems, Signal Processing and Their Applications. Tipaza, Algeria, 2011: 283-286. |
| [5] | YUAN J T, CHAO J H, LIN T C. Effect of channel noise on blind equalization and carrier phase recovery of CMA and MMA[J]. IEEE Transactions on Communications, 2012, 60(11): 3274 -3285. |
| [6] | YANG Jing, WERNER J J, DUMONT G A. The multimodulus blind equalization and its generalized algorithms[J]. IEEE Journal on Selected Areas in Communications, 2002, 20(5): 997-1014. |
| [7] | 郭业才. 自适应盲均衡技术[M]. 合肥: 合肥工业大学出版社, 2007: 17-24. |
| [8] | NI Youcong, DU Xin, XIAO Ruliang, et al. Multi-modulus blind equalization algorithm based on high-order QAM genetic optimization[C]// Eighth International Conference on Natural Computation (ICNC). Chongqing, China, 2012: 679-682. |
| [9] | 郭业才, 张艳萍. 一种适用于高阶QAM信号的双模式多模盲均衡算法[J]. 系统仿真学报, 2008, 20(6): 1423-1426.GUO Yecai, ZHANG Yanping. Dual-model multi-modulus blind equalization algorithm for high-order QAM signals[J]. Journal of System Simulation, 2008, 20(6): 1423-1426. |
| [10] | LIU Feng, GE Lindong, LI Jiaming,et al. New multi-modulus algorithms for blind decision-feedback equalization of high-order QAM signals[C]//Innovative Computing Information and Control(ICICIC). Dalian, China, 2008: 386. |
| [11] | YANG Xinshe. Nature-inspired metaheuristic algorithms[M]. 2nd ed. Frome, UK: Luniver Press, 2010: 97-104. |
| [12] | YANG Xinshe. A new metaheuristic bat-inspired algorithm[M]// Nature Inspired Cooperative Strategies for Optimization. Berlin/Heidelberg: Springer, 2010: 65-74. |
| [13] | AFRABANDPEY H, GHAFFARI M, MIRZAEI A, et al. A novel bat algorithm based on chaos for optimization tasks[C]//Iranian Conference on Intelligent Systems (ICIS). Bam, 2014: 1-6. |
| [14] | BISWAL S, BARISAL A K, BEHERA A, et al. Optimal power dispatch using BAT algorithm[C]//International Conference on Energy Efficient Technologies for Sustainability (ICEETS). Nagercoil, 2013: 1018-1023. |
| [15] | SAJI Y, RIFFI M E, AHIOD B. Discrete bat-inspired algorithm for travelling salesman problem[C]//Second World Conference on Complex Systems (WCCS). Agadir, Morocco, 2014: 28-31. |



