自然界中普遍存在着群体行为,例如鸟的成群结队、鱼和昆虫协作捕食等,都显示出一些群体特质:相对简单的生物个体可以通过群体共同完成更为复杂的任务。自然界中的群体行为使得它们能够很好地生存繁衍下去,同时也给人类很大的启发:与单个智能体相比,多智能体系统的合作可以大大提高系统的性能,完成更复杂的任务。
多智能体技术是近年来新兴的一门控制学科,它具有自主性、协调性、自组织能力和推理能力等特点。采用多智能体系统解决问题在鲁棒性、可靠性和对未知环境的适应性等方面也有很多的潜在优势[1]。因此,多智能体系统的研究已经成为控制领域的一个热点[2, 3, 4],并且已经广泛的应用在各个领域,如智能交通、机器人的编队控制,甚至是军事用途[5, 6, 7, 8, 9, 10, 11]。
智能体系统研究的核心问题是能控性问题,能控性是现代控制理论的一个基本概念,由卡尔曼(Klaman)在20世纪60年代首次提出[12]。多智能体系统的能控性是指基于系统内部智能体之间的相互连接关系,通过对多智能体内部的领航者施加外部控制输入,使得跟随者由任意给定的初始状态到达期望的最终状态。能控性能使每个智能体的状态达到人们预定的结果,使系统发挥最大的作用,因此多智能体系统能控性的研究具有非常重要的意义。Tanner在2004年最早提出了多智能体网络系统的能控性概念,叙述了单输入线性系统领航-跟随者的经典可控性,即领航者接受外部控制信号,对跟随者发布指令,从而影响跟随者的运动。但是这种结构的引入也带来了新的问题,如领航者的选取,领航者的丢失问题等[13]。文献[14]提出了控制协议,介绍了多智能体网络系统能控的代数条件和图论条件。近年来,越来越多的研究者开始从图论的角度研究多智能体的能控性[15, 16],拓展了多智能体系统能控性的理论研究范围。多智能体网络系统的能控性不仅在理论方面具有重要研究价值,同时也具有重要的实践意义,例如可以借助多智能体网络研究编队控制,即通过调整领航者的行为来驱动跟随者达到理想的位置[17]。很多现实中的网络,如社交网络、电网、食物网和神经网络等都存在内在节点间的动态关系,但是文献[13, 14, 15, 16, 17, 18]没有考虑到节点之间具有内在动力的情况。因此,从理论和实践的角度来看,异构动态多智能体网络系统的可控性研究具有极其重要的意义和价值[19, 20]。Cai基于高阶异质多智能体系统的分析建立了复杂异质多智能体系统模型,并且提出了系统不能控的2个充分条件[21, 22, 23, 24, 25, 26, 27, 28]。Ji等研究了具有状态时间延迟和切换拓扑的多智能体系统的能控性[22, 23, 24]。Liu研究了含多个领航者和时滞情况下切换离散时间多智能体系统的能控性,提出系统的能控性仅仅是由领航者与跟随者之间的交互信息所决定的[25]。在绝对协议下,文献[26, 27]研究了在广播控制信号下多智能体系统的能控性。与领航者-跟随者结构相比,广播信号在现实生活中应用更为广泛。文献[28]研究了一致性协议下单智能体的能控性。本文基于相对协议和绝对协议,总结了多智能体网络系统的模型和能控性的代数条件。总结了在绝对协议下多智能体网络系统的模型和能控性的代数条件,指出了该领域新的研究方向。
1 图论的准备知识本文使用的通信结构均为无向图,关于无向图更全面的内容见文献[29]。
一个无向图G=(V,E)包括一个顶点集V={v1,v2,…,vn}和一个边集E={(vi,vj)|vi,vj∈V},边是指在图G里不同的无序节点对。如果节点vi,vj∈V,并且互为邻居,那么它们之间的关系可以用vi~vj表示。令Ni表示节点i的邻居集,Ni=j|vi~vj。路径vi0vi1…vis是一个vik-1~vik,k=1,2,…,s的有限序列。如果在任意2个不同的节点对之间都有路径,那么就说G是连通的。完备图是指图中任意2个节点都是相邻的关系。图G=(V,E)是无向图,其中vi∈V,与节点vi邻接的节点数就是vi的度数。不含圈和重边的无向图称为简单图。各顶点的度均相同的无向简单图称为正则图。
图G的度矩阵D(G)是一个对称矩阵,它的对角线元素就是节点的度数。图G的邻接矩阵A(G)表达了图G中各顶点之间的相邻关系,任意一个无向图都可以由邻接矩阵A(G)来表示,它是一个只含有元素0和元素1的对称矩阵,如果节点vi和vj是相邻的,则aij是1,否则就是0。图的拉普拉斯矩阵L(G)是一个实对称矩阵,它定义为度矩阵与邻接矩阵之差:L(G)=D(G)-A(G),经过计算可得: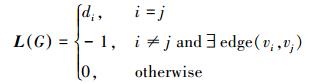
多智能体网络系统的相对协议是ui=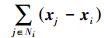 。本节基于相对协议,总结了多智能体网络系统能控性的模型和代数条件,同时提出了一些新的代数条件。
。本节基于相对协议,总结了多智能体网络系统能控性的模型和代数条件,同时提出了一些新的代数条件。
将按照从一阶同质多智能体网络系统到高阶同质多智能体网络系统的方式,对能控性代数条件进行总结。
2.1.1 一阶同质多智能体网络系统的能控性采用多智能体系统如下:
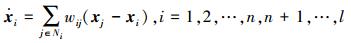
f=[x1x2 … xn]T,xl=[xn+1 xn+2 … xn+l]T,系统(1)可以写成如下形式:
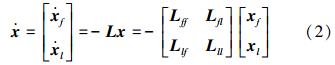
式中:xf和x l分别代表跟随者和领航者状态的迭加向量, Lff∈ Rn×n和L ll∈Rl×l分别对应于系统跟随者和领航者的编号,Llf表示从跟随者到领航者的通信连接关系,Lfl表示从领航者到跟随者的通信连接关系。只要系统中的领航者能驱动跟随者到达期望的状态,那么系统就是可控的。本文研究的能控性问题是领航者对跟随者的控制能力,即系统(3)的能控性问题。
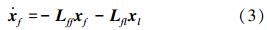
如果存在输入信号u(t),能使系统在规定的时间内从任意的初始状态xf(0)被驱使到理想状态xf(T),则系统(3)是能控的。
定义1[30] 如果将矩阵L划分成式(2)的形式,最后l个智能体为领航者,当且仅当Lff, Lfl可控,则系统就是能控的。
引理1[31] 给定系统 ·f=-Lffxf-Lflxl,可以得出以下的说法是等同的:
·f=-Lffxf-Lflxl,可以得出以下的说法是等同的:
1)系统是能控的;
2)能控性矩阵
[-Lfl LffLfl -L2ffLfl … (-1)nLffn-1Lfl]是行满秩的;3)对于系统所有的特征值λ∈R,矩阵对[λI-Lff Lfl]都是行满秩的,也就是说如果vTL ff=λvT则 vTL fl≠0,其中v是矩阵Lff的特征值λ所对应的非零的左特征向量。
注释1 学术界已经广泛研究了一阶动力学多智能体网络系统的模型,例如文献[13, 14, 15, 16, 17, 18]。而系统(1)是一般的加权系统模型。
命题1 系统(3)是能控的,也就是[Lff Lfl]是可控的,那么当且仅当矩阵L和矩阵Lff没有相同的特征值。
定理1 系统(3)是可控的,即矩阵对[Lff Lfl]是可控的,那么矩阵L不存在与领航者节点所对应向量元素全为0的左特征向量。
证明 根据引理1,如果矩阵Lff中存在与特征值λ所对应的左特征向量vf∈Cn,使得vfTLfl=0成立,那么矩阵对[Lff Lfl]是不可控的。构造一个向量v∈Cn+l,令vT=[vfT 0],那么下式成立:
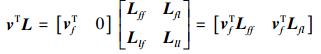
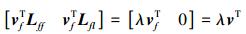
所以vTL=λvT。这说明向量v 是L的左特征向量,并且对应于所有领航者的最后l项全为零元素。因此定理1成立。
2.1.2 高阶同质多智能体网络系统的能控性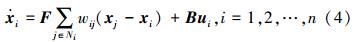
式中:xi∈Rd,F∈Rd×d,wij∈R,B∈Rd×m,ui∈Rm; xi表示智能体i的状态;wij表示图G的边权重,代表了节点i和j之间的连接强度;B是控制输入矩阵。如果输入ui=0,那么智能体i就是跟随者,反之就是领航者。定义x=[x1Tx2T … xnT]T∈Rd×n,u=[u1T u2T … unT]T∈Rm×n,则系统(4)就可以写成

假设前q个智能体是领航者,那么

注释2 文献[21, 32]的状态方程为 ·=-FXLT+BU。为了使分析一致,将
·=-FXLT+BU。为了使分析一致,将 ·=-FXLT+BU进行拉直处理转化成式(5)进行分析。
·=-FXLT+BU进行拉直处理转化成式(5)进行分析。
引理2 实矩阵A、B、C、D的维数兼容,那么有以下结论[33]:
1)(A+B)ⓧC=AⓧC+BⓧC
2)(AⓧB)(CⓧD)=(AC)ⓧ(BD)
3)(AⓧB)T=ATⓧBT
4)A为m×m的矩阵,它的特征值 λ1,λ2,…,λm所对应的左特征向量分别是 α1,α2,…,αm, B为n×n的矩阵,它的特征值 μ1, μ2,…,μn所对应的左特征向量分别是 β1,β2,…,βn。则 AⓧB的特征值是λiμj(i=1,2,…,m;j=1,2,…,n),对应的左特征向量是α iⓧβj。
定理2[21] 要使系统(5)能控,那么以下2个条件必须同时成立。
1)[F B]是一个能控矩阵对;
2)矩阵L不存在前q项全是零元素的左特征向量。
证明 根据PBH判据,如果系统(5)是不可控的,那么矩阵LⓧF中存在与特征值λ相对应的左特征值向量v,使得vT(ΛⓧB)=0成立。假设矩阵L和F对应的左特征向量分别是α∈Cn和β∈Cd,由引理2可知,v=αⓧβ和(αTⓧβT)(ΛⓧB)=0同时成立,所以得到
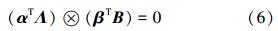
要使式(6)成立,则有以下2种情况:
1)如果αTΛ=0,也就是说矩阵L存在这样的左特征向量,其前q项都是零元素;或者
2)βTB=0,即[F B]是不可控的。
分析以上2种情况,可知定理2成立。
2.2 异质多智能体网络系统的能控性按照从简单异质多智能体网络系统到复杂异质多智能体网络系统的顺序对能控性的线性代数条件进行总结。
2.2.1 简单异质多智能体网络系统的能控性1)领航-跟随者框架下简单异质多智能体网络系统的模型与文献[19]相似:
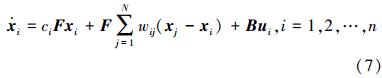
式中:xi∈Rd,ci∈R,F∈Rd×d,wij∈R,B∈Rd×m,ui∈Rm。ciFxi表示节点i之间的内部动态关系。如果输入ui=0,那么智能体i就是跟随者,否则就是领航者。定义X=[x1Tx2T … xTn]T∈Rdn,U=[u1T u2T … un T]T∈ Rmn,则系统(7)可以写成:
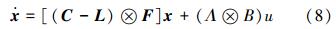
如果系统的前q个智能体是领航者,那么
C=diag(c1,c2,…,cn),
定理3[19] 要使系统(8)能控,那么以下2个条件必须同时成立。
1)[F B]是一个能控矩阵对;
2)(C-L)不存在前q项都为零的左特征向量。
证明 定理3的证明过程与定理2相似。
2)广播信号下简单异质多智能体网络系统的模型与文献[20]中相似,系统模型为
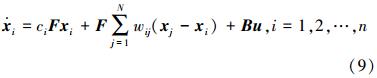
式中:xi∈Rd,ci∈R,F∈Rd×d,wij∈R,B∈Rd×m,u∈Rm。ciFxi表示节点i之间的内部动态关系。由于系统(9)中所有的智能体都接收相同的控制信号,所以称u为广播控制信号。定义X=[x1T x2T … xnT]T∈Rdn,U=[u1T u2T … unT]T∈Rmn,则系统(9)可以写成如下形式:
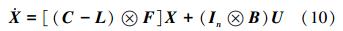
命题2[19] 如果系统(10)是能控的,那么当且仅当以下2个条件同时满足:
1)[F B]是一个能控矩阵对;
2)矩阵(C-L)ⓧF的所有特征值各不相同。
2.2.2 复杂异质多智能体网络系统的能控性文献[21]的复杂异质多智能体网络系统写成
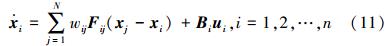

将方程(12)与方程(1)相比较,如果把方阵Mij∈Rd×d看作是拓扑图G的边权重,那么系统的邻接矩阵为
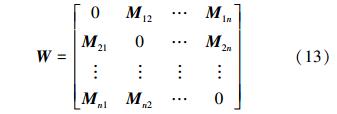
系统对应的拉普拉斯矩阵为
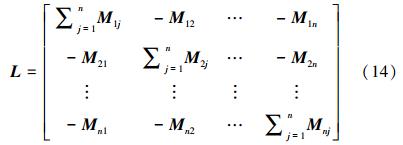
注释3 文献[19]中,ci∈R表示节点i之间的异质动态关系,文献[21]中Fij∈ Rd×d表示节点i之间的异质动态关系。文献[21]的异质多智能体网络系统的能控性是非常复杂的,所以对于这样一个异质网络系统,只得到了系统不能控的2个充分条件。
命题3[21] 如果方程(11)表示的加权矩阵图是双向的,即Mik=Mki(∀i,k=1,2,…,n),并且矩阵对的集合MikBii,k=1,2,…,n是不能控的,那么多智能体系统(10)就是不能控的。
命题4[21] 如果文献[21]中异质多智能体系统的拓扑图G是结构不能控的,那么整个系统都是不能控的。
2.3 一般多智能体网络系统的能控性采用文献[25]的一般动力学多智能体网络系统模型:

式中:xi∈R p代表智能体i的状态,u i∈Rs是智能体i的耦合变量,ul∈ Rq是智能体i的外部输入。A=Rp×p,B∈R p×q,C∈Rp×s。
每个智能体i的耦合变量ui∈Rs是由邻居间的耦合扩散变量决定的。也就是说,系统的相对协议为
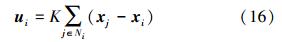
令x=col(x1,x2,…,xn), u=col(u1,u2,…,um),则系统(15)可以写成矩阵形式:

式中: =InⓧA-Lⓧ(CK),
=InⓧA-Lⓧ(CK), =MⓧB,M∈Rn×m。m是领航者的数目。
=MⓧB,M∈Rn×m。m是领航者的数目。

定理4[25] ( ,
, )是能控的,当且仅当以下2个条件同时成立:
)是能控的,当且仅当以下2个条件同时成立:
1)(L,M)是能控的;
2)对于矩阵L的每一个特征值λ,矩阵对(A-λCK,B)都是可控的。
证明 (必要性)只证明矩阵(L,M)能控的必要条件,(A-λCK,B)能控的必要条件可以用相似的方法来证明。假设(L,M)是不能控的,则存在非零向量 x∈Rn使得x TL=λ xT和x TM=0成立。令(θ,y)∈C×Cp是矩阵(A- λCK,B)的左特征向量,那么

由xTL=λxT,可得x
TL/λ=xT,即L/λ=
In。所以式(18)可转化成
1/λ{Lⓧ(A-λ
CK)}=1/λ{LⓧA
-λLⓧCK}=
InⓧA-LⓧCK= 。由引理2,(
θ,xⓧy)是
。由引理2,(
θ,xⓧy)是 的一个左特征向量,则有
的一个左特征向量,则有

通过PBH判据可知,( ,
, )是不可控的。
)是不可控的。
(充分性)假设( ,
, )是不能控的。由于L是对称矩阵,总能找到一个正交矩阵U使L=UDUT成立[33],即
)是不能控的。由于L是对称矩阵,总能找到一个正交矩阵U使L=UDUT成立[33],即
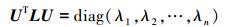
 和
和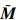 :
:
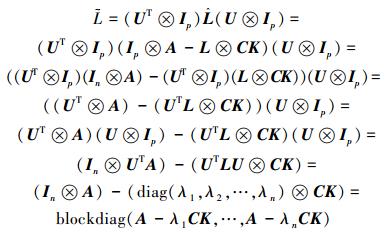

由于( ,
, )是不能控的,并且UTⓧIp是非奇异的,因此矩阵对(
)是不能控的,并且UTⓧIp是非奇异的,因此矩阵对(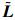 ,
,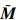 )也是不能控的。考虑到
)也是不能控的。考虑到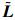 的块对角结构,那么就一定会存在一个数s,1≤s≤n,使与它相对应的矩阵对(A-λsCK,(UTM)sⓧB)是不能控的。用(M)s表示矩阵M的第s行。因此,
的块对角结构,那么就一定会存在一个数s,1≤s≤n,使与它相对应的矩阵对(A-λsCK,(UTM)sⓧB)是不能控的。用(M)s表示矩阵M的第s行。因此,
1)(UTM)s=0,也就是说(L,M)是不能控的;
2)假如(UTM)s≠0,那么(A-λsCK,B)是不能控的。
因此矛盾,故结论成立,定理证明完毕。
注释4 定理4的证明比较复杂,是一个新的证明方法,并且有一定的参考价值。
3 绝对协议下多智能体网络系统的能控性在绝对协议 下,总结动力学多智能体网络系统能控性的代数条件,并且提出了一些新的代数条件。
下,总结动力学多智能体网络系统能控性的代数条件,并且提出了一些新的代数条件。
采用文献[26]的多智能体网络系统模型,它由广播信号控制:

式中:xi表示智能体i的状态,Ni={j|vi~vj;j≠i}是节点vi的邻居集,u是控制输入。多智能体系统(20)的所有智能体都接受相同的控制信号,即u,称这个信号为广播信号。
系统(20)可以写成如矩阵形式如下:

式中:A∈Rn×n为多智能体系统的邻接矩阵,b=[1 1 … 1]T∈Rn。
命题5[13] 当且仅当以下2个条件同时成立,系统(21)是能控的。
1)矩阵A的特征值各不相同;
2)A的特征向量都不与b正交。
注释5 命题5证明过程见文献[13]。但是命题5只要满足条件2)系统就是能控的,即条件2)是系统能控的充要条件,条件1)是系统能控的必要条件。
定理5 当且仅当矩阵A的所有特征向量都不正交于b,则系统(21)是能控的,并且如果系统(21)是能控的,那么矩阵A的特征值各不相同。
证明 假设向量v是矩阵A的特征向量,在PBH判据的条件下,如果系统(21)是能控的,那么rank(λiI-A,b)=n成立。将PBH判据和对称的状态矩阵结合起来,如果系统是不能控的,那么矩阵A存在一个特征向量使得(λiI-A,b)vT=0成立,则有
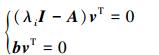
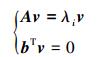
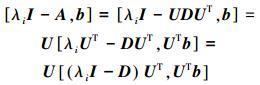
向量vi是特征值λi所对应的特征向量,即v=(v1,v2,…,vn)。由于U是非奇异矩阵,所以它不影响[(λiI-D)UT UTb]的秩,只需考虑[(λiI-D)UT UTb]是否满秩。将λiI-DUT UTb展开:

从式(22)可以看出,要使系统(21)是能控的,则矩阵A的所有特征值各不相同。
3.2 高阶异质多智能体网络系统的能控性给定多智能体系统模型:

式中:xi∈Rd,ci∈R,F∈Rd×d,B∈Rd×m,和ui∈Rm。ciFxi表示异质多智能体系统中节点i之间的动态关系。如果输入ui=0,那么智能体i就是跟随者,反之是领航者。
令x=[x1T x2T … xnT]T∈Rd×n以及u=[u1T u2T … unT]T∈Rm×n,则系统(23)可以写成如下形式:
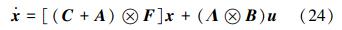
式中:C=diag(c1,c2,…,cn),A∈Rn×n是系统的邻接矩阵。如果前q个智能体是领航者,那么Λ=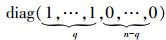 。
。
定理6 假设F是对称的,如果系统(24)是能控的,那么必须同时满足以下2个条件:
1)[F B]是一个能控矩阵对;
2)矩阵(C+A)不存在前q个元素都是零元素的左特征向量。
证明 假设系统(24)是不能控的,根据PBH判据,(C+A)ⓧF就存在左特征向量v使得vT(ΛⓧB)=0成立。根据引理2,矩阵(C+A)和矩阵F分别存在特征向量v1和v2使得P=v1ⓧv2和(v1Tⓧv2T)(InⓧB)≠0成立,那么
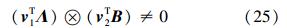
当且仅当以下2个条件同时满足时,式(25)成立。
1)v1TΛ≠0,也就是说(C+A)不存在前q项都是零元素的左特征向量;
2)v2TB≠0,也就是说[F B]是一个能控矩阵对。
显然,定理6成立。
4 结束语本文探究了多智能体网络系统的能控性问题,分别在相对协议和绝对协议下总结了多智能体网络系统的部分模型和能控性的线性代数条件。相对协议下,主要在Leader-Follower模型下利用已有的能控性代数条件对一阶系统和高阶系统的能控性代数条件进行了总结和改进,并且还总结了一般多智能体网络系统模型下能控性的充分必要条件。在绝对协议下,研究了广播信号下能控性的充分必要条件,使能控性的充要条件得到了简化。此外,本文不仅讨论了同质多智能体网络系统的能控性,还讨论了异质多智能体网络系统的能控性问题。由于自然现象和实际应用中,不同生物群体之间动力学具有较大的差别,异质多智能体网络系统的能控性问题是未来研究的一个重要方向,所以本文对异质多智能体网络系统能控性研究结果也具有很大的实际意义。
| [1] | LIM H, KANG Y, KIM J, et al. Formation control of leader following unmanned ground vehicles using nonlinear model predictive control[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Singapore, 2009: 945-950. |
| [2] | JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988-1001. |
| [3] | FAX J A. Optimal and cooperative control of vehicle formations[M]. Pasadena: California Institute Technology, 2001: 1-11. |
| [4] | OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533. |
| [5] | 刘金琨, 尔联洁. 多智能体技术应用综述[J]. 控制与决策, 2001, 16(2): 133-140, 180. LIU Jinkun, ER Lianjie. Overview of application of multiagent technology[J]. Control and Decision, 2001, 16(2): 133-140, 180. |
| [6] | FAX J A, MURRAY R M. Information flow and cooperative control of vehicle formations[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1465-1476. |
| [7] | OGREN P, FIORELLI E, LEONARD N E. Cooperative control of mobile sensor networks: adaptive gradient climbing in a distributed environment[J]. IEEE Transactions on Automatic Control, 2004, 49(8): 1292-1302. |
| [8] | MU S M, CHU T G, WANG L. Coordinated collective motion in a motile particle group with a leader[J]. Physica A: Statistical Mechanics and its Applications, 2005, 351(2-4): 211-226. |
| [9] | HONG Y G, HU J P, GAO L X. Tracking control for multi-agent consensus with an active leader and variable topology[J]. Automatica, 2006, 42(7): 1177-1182. |
| [10] | SHI H, WANG L, CHU T G. Virtual leader approach to coordinated control of multiple mobile agents with asymmetric interactions[J]. Physica D: Nonlinear Phenomena, 2006, 213(1): 51-65. |
| [11] | LANE D M, MCFADZEAN A G. Distributed problem solving and real-time mechanisms in robot architectures[J]. Engineering Applications of Artificial Intelligence, 1994, 7(2): 105-117. |
| [12] | KALMAN R E. Mathematical description of linear dynamical systems[J]. Journal of the Society for Industrial and Applied Mathematics Series A: Control, 1963, 1(2): 152-192. |
| [13] | TANNER H G. On the controllability of nearest neighbor interconnections[C]//Proceedings of the 43rd IEEE Conference on Decision and Control. Atlantis, Paradise Island, Bahamas, 2004: 2467-2472. |
| [14] | RAHMANI A, MESBAHI M. On the controlled agreement problem[C]//Proceedings of the 2006 American Control Conference. Minneapolis, USA, 2006: 1376-1381. |
| [15] | RAHMANI A, JI M, MESBAHI M, et al. Controllability of multi-agent systems from a graph-theoretic perspective[J]. SIAM Journal on Control and Optimization, 2009, 48(1): 162-186. |
| [16] | JI M, EGERSTEDT M. A graph-theoretic characterization of controllability for multi-agent systems[C]//Proceedings of the IEEE American Control Conference. New York, USA, 2007: 4588-4593. |
| [17] | JI Z J, WANG Z D, LIN H, et al. Interconnection topologies for multi-agent coordination under leader-follower framework[J]. Automatica, 2009, 45(12): 2857-2863. |
| [18] | DAVISON E J. Connectability and structural controllability of composite systems[J]. Automatica, 1977, 13(2): 109-123. |
| [19] | XIANG L Y, ZHU J J H, CHE F, et al. Controllability of weighted and directed networks with nonidentical node dynamics[OL/EB].[2014-01-20]. http://www.hindawi.com/journals/mpe/2013/405034. |
| [20] | 王晓晓, 纪志坚. 广播信号下非一致多智能体系统的能控性[J]. 智能系统学报, 2014, 9(4): 401-406. WANG Xiaoxiao, JI Zhijian. Controllability of non-identical multi-agent systems under a broadcasting control signal[J]. CAAI Transactions on Intelligent Systems, 2014, 9(4): 401-406. |
| [21] | CAI N, CAO J W, LIU M H, et al. On controllability problems of high-order dynamical multi-agent systems[J]. Arabian Journal for Science and Engineering, 2014, 39(5): 4261-4267. |
| [22] | LIU B, CHU T G, WANG L, et al. Controllability of a leader-follower dynamic network with switching topology[J]. IEEE Transactions on Automatic Control, 2008, 53(4): 1009-1013. |
| [23] | JI Z J, WANG Z D, LIN H, et al. Controllability of multi-agent systems with time-delay in state and switching topology[J]. International Journal of Control, 2010, 83(2): 371-386. |
| [24] | ZHANG S, CAO M, CAMLIBEL M K. Upper and lower bounds for controllable subspaces of networks of diffusively coupled agents[J]. IEEE Transactions on Automatic Control, 2014, 59(3): 745-750. |
| [25] | LIU B, SU H S, LI R, et al. Switching controllability of discrete-time multi-agent systems with multiple leaders and time-delays[J]. Applied Mathematics and Computation, 2014, 228: 571-588. |
| [26] | YOON M G, ROWLINSON P, CVETKOVI D, et al. Controllability of multi-agent dynamical systems with a broadcasting control signal[J]. Asian Journal of Control, 2014, 16(4): 1066-1072. |
| [27] | NI W, WANG X L, XIONG C. Consensus controllability, observability and robust design for leader-following linear multi-agent systems[J]. Automatica, 2013, 49(7): 2199-2205. |
| [28] | Yoon M G. Single agent control for cyclic consensus systems[J]. International Journal of Control, Automation and Systems, 2013, 11(2): 243-249. |
| [29] | GODSIL C, ROYLE G. Algebraic Graph Theory[M]. New York: Springer, 2001: 163-171. |
| [30] | CAI N, ZHONG Y S. Formation controllability of high-order linear time-invariant swarm systems[J]. IET Control Theory & Application, 2010, 4(4): 646-654. |
| [31] | CHEN C T. Linear system theory and design[M]. New York: Oxford University Press, 1999: 6. |
| [32] | CAI N, CAO J W, KHAN M J. A controllability synthesis problem for dynamic multi-agent systems with linear high-order protocol[J]. International Journal of Control, Automation and Systems, 2014, 12(6): 1366-1371. |
| [33] | HORN R A, Johnson C R. Matrix analysis[M]. Cambridge: Cambridge University Press, 1985: 11-14. |



