2. 西南交通大学 智能控制开发中心, 四川 成都 610031
2. Intelligent Control Development Center, Southwest Jiaotong University, Chengdu 610031, China
在人工智能领域,知识表示的方式多种多样,子句形式仍不失为一种重要的知识表达方式。子句表示广泛应用于机器定理证明、专家系统和知识库等领域。在一个知识库中,如果有部分知识可以删除并且不减少整个知识库携带的信息,那么称这个知识库是冗余的。冗余以及与其密切相关的化简已经成为具有重要现实意义的问题。命题逻辑中子句由文字的析取组成,因此能够对其中的文字进行科学合理的分类对研究冗余文字和冗余子句很有必要,这些理论为归结自动推理奠定了基础。
逻辑公式的化简是计算机科学和人工智能领域重要的研究方向。逻辑上的冗余问题已被许多学者广泛研究[1, 2, 3, 4],包括不同计算问题的复杂性的刻画。其中,主要包括冗余性在实际可满足性求解中的重要作用的研究[5, 6, 7, 8, 9, 10, 11]。 P.Liberatore[1]对命题逻辑中的子句集进行了分类,给出了冗余子句的一些等价条件和性质。翟翠红等[12]研究了命题逻辑中的冗余子句和冗余文字,讨论了子句集的无冗余等价子集。唐世辉[13]研究了命题逻辑中子句集的冗余性,将命题逻辑中子句分为绝对冗余、相对冗余和无冗余3类。因此,本文主要深入研究命题逻辑的子句集中文字的特征,将命题逻辑的子句集中的文字划分为有用文字、必需文字和无用文字,讨论3种文字的关系。最后得到有用文字、必需文字和无用文字的判定方法,为命题逻辑公式的化简提供理论支撑。
1 预备知识在命题逻辑公式中,称原子公式及其否定叫做文字,有限多个文字的析取叫子句,只含有一个文字的子句称为单子句。
定义1[14] 设A(p1,p2,…,pm)∈F(S),则当A具有形式(Q11∨Q12∨…∨Q1n)∧…∧(Qm1∨Qm2∨…∨Qmn)时,称A为合取范式(conjunction normal form,CNF),这里Qij=pj或Qij=¬pj (j=1,2,…,n;i=1,2,…,m)。
定义2[15] 设S={C1,C2,…,Cm,D}是命题逻辑中的子句集。显然,D是S中的冗余子句,当且仅当C1∧C2∧…∧Cm∧D≡C1∧C2∧…∧Cm。
一个子句是冗余的,暗示此子句可以从子句集中删除,不会影响子句集所要表示的信息。同理,一个子句集是冗余的,可以定义为它和它的一个真子集等价。
定义3[1] 子句集S是冗余的,当且仅当存在S′⊂S,使S′=S。
在命题逻辑中,此定义和如下说法是等价的:
1)存在S′⊂S,使S′⊨S;
2)S中含有冗余子句。
定义4[1] 设S是子句集,C∈S,
1)称C在S中是必需的(necessary),如果对于S的任一无冗余等价子集S′,有C∈S′;
2)称C在S中是有用的(useful),如果存在S的一个无冗余等价子集S′,使C∈S′;
3)称C在S中是无用的(useless),如果对于S的任一无冗余等价子集S′,有C∉S′。
定理1[1] 设S是子句集,C∈S,C在S中是必需的当且仅当S-{C}⊭C。
定理2[12] 设S是子句集,C∈S。 C在S中是有用的当且仅当存在S的一个无冗余等价子集S′,使S′-{C}⊭C。
定理3[12] 设S是子句集,C∈S。 C在S中是无用的当且仅当S的无冗余等价子集恰为S-{C}的无冗余等价子集。
定理4[13] 设S={C1,C2,…,Cm,D}是命题逻辑中子句集,且D中不含互补文字。D是S中冗余子句当且仅当子句集S′={C1,C2,…,Cm}∪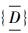 不可满足。
不可满足。
定义5[12] 设S={C1,C2,…,Cm,D}是命题逻辑中子句集,D=x∨D1,其中x是一文字,D1是一子句,如果D∧C1∧C2∧…∧Cm=D1∧C1∧C2∧…∧Cm,则称x是D中关于S的冗余文字。
定理5[12] 设S={C1,C2,…,Cm,D}是命题逻辑中的子句集,D=x∨D1,如果D1是S′={C1,C2,…,Cm,D1}中的冗余子句,则x是D中关于S的冗余文字。
定理6[12] 设S={C1,C2,…,Cm,D}是命题逻辑中子句集,D=x∨D1,x是D中关于S的冗余文字当且仅当D1是子句集S′={D1,x,C1,C2,…,Cm}中的冗余子句。
定理7[12] 设S={C1,C2,…,Cm,D}是命题逻辑中子句集,且D中不含互补文字。D是S中冗余子句当且仅当子句集S′={C1-D,C2-D,…,Cm-D}不可满足。
对于子句集S,令S|x={C|C∈S且{x,¬x}∩C∅}∪{C\{¬x}|C∈S且¬x∈C},S|A=(…((S|x1)|x2)…|xn),其中A={x1,x2,…,xn}。
定理8[13] 设S={C1,C2,…,Cm,D}是命题逻辑中子句集,子句集S′={C1,C2,…,Cm}∪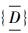 不可满足当且仅当子句集(S\{D})|
不可满足当且仅当子句集(S\{D})|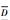 不可满足。
不可满足。
定义6 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,若有Ci=x∨Di(i∈{1,2,…,m}),其中x是一文字,Di是一子句,且x不是Ci中关于S的冗余文字,则称x是S中的必需文字。
定义7 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果存在S中的一个子句Ci,若有Ci=x∨D(i∈{1,2,…,m}),其中x是一文字,D是一子句,且x不是Ci中关于S的冗余文字,则称x是S中的有用文字。
定义8 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,若有Ci=x∨Di(i∈{1,2,…,m}),其中x是一文字,Di是一子句,且x是Ci中关于S的冗余文字,则称x是S中的无用文字。
从定义6~8可以看出,子句集中的必需文字一定是有用文字,有用文字不一定是必需文字,同时有用和无用是2个相对的概念,子句集中的必需文字一定是非冗余文字,子句集中的无用文字一定是冗余文字。
定理9 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,若有Ci=x∨Di(i∈{1,2,…,m}),其中x是一文字,Di是一子句,x是S中的必需文字当且仅当S′i-{Di}⊭Di,S′i={Di,x,C1,…,Ci-1,Ci+1,…,Cm}(i∈{1,2,…,m})。
证明 因为x是S中的必需文字,所以x一定不是Ci关于S的冗余文字,由定理6知x不是Ci中关于S的冗余文字当且仅当Di不是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}(i∈{1,2,…,m})中的冗余子句,因此Di在Si′中是必需的,由定理1知Di在Si′中是必需的当且仅当Si′-{Di}⊭Di。
推论1 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果存在S中的一个子句Ci,若有Ci=x∨D(i∈{1,…,m}),其中x是一文字,D是一子句,则x是S中的有用文字当且仅当S′-{D}⊭D,其中S′={D,x,C1,…,Ci-1,Ci+1,Cm}。
定理10 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果存在S中的一个子句Ci,若有Ci=x∨D(i∈{1,2,…,m}),其中x是一文字,D是一子句,则x是S中的有用文字当且仅当存在S′的一个无冗余等价子集S″使S″-{D}⊭D,其中S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}。
证明 因为x是S中的有用文字,所以x一定不是Ci关于S的冗余文字,由定理6知x不是Ci中关于S的冗余文字当且仅当D不是子句集S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,因此D在S′中是有用的,由定理2知D在S′中是有用的当且仅当存在S′的一个无冗余等价子集S″使S″-{D}⊭D,S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}。
定理11 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,若有Ci=x∨Di(i∈{1,2,…,m}),其中x是一文字,Di是一子句,则称x是S中的无用文字当且仅当Si′的无冗余等价子集恰为Si′-{Di}的无冗余等价子集,其中S′i={Di,x,C1,…,Ci-1,Ci+1,…,Cm}(i∈{1,2,…,m})。
证明 因为x是S中的无用文字,所以x一定是Ci关于S的冗余文字,由定理6知x是Ci中关于S的冗余文字当且仅当Di是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}(i∈{1,…,m})中的冗余子句,因此Di在Si′中是无用的,由定理3知Di在Si中是无用的当且仅当Si′的无冗余等价子集恰为Si′-{Di}的无冗余等价子集。
3 子句集中文字的判定根据子句集中文字的分类和冗余子句与子句集的可满足性判定的关系可以得到如下定理。
定理12 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,有Ci=x∨Di(i∈{1,2,…,m}),其中x是一文字,Di是一子句,且Di中不含互补文字,则x是S中的无用文字当且仅当子句集{x,C1-Di,…,Ci-1-Di,Ci+1-Di,…,Cm-Di}(i∈{1,2,…,m})不可满足。
证明 若x是S中的无用文字,则一定存在Ci∈S且Ci=x∨Di,使x是Ci中关于S的冗余文字,则Di是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,于是由定理7知Di是子句集Si′={Di,x,C1…,Ci-1,Ci+1,…,Cm}中的冗余子句当且仅当子句集{x,C1-Di,…,Ci-1-Di,Ci+1-Di,…,Cm-Di}不可满足。
定理13 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,有Ci=x∨Di(i∈{1,2,…,m}),其中x是一文字,Di是一子句,且Di中不含互补文字,则x是S中的必需文字当且仅当子句集{x,C1-Di,…,Ci-1-Di,Ci+1-Di,…,Cm-Di}(i∈{1,2,…,m})可满足。
证明7 (充分性)若x不是S中的必需文字,则存在Ci∈S且Ci=x∨Di,使x是Ci中关于S的冗余文字,则Di是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,即Di∧x∧C1∧…∧Ci-1∧Ci+1∧…∧Cm=x∧C1∧…∧Ci-1∧Ci+1∧…∧Cm。又因为Ci=x∨Di,所以xDi,即x-Di=x。于是由定理7知子句集{x,C1-Di,…,Ci-1-Di,Ci+1-Di,…,Cm-Di}(i∈{1,2,…,m})不可满足,矛盾。
(必要性)假设子句集{x,C1-Di,…,Ci-1-Di,Ci+1-Di,…,Cm-Di}不可满足,由定理7知Di是子句集Si′={Di,x,Ci,…,Ci-1,Ci+1,…,Cm}中的冗余子句,则x不是S中的必需文字,矛盾。
定理14 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果存在S中的一个子句Ci,若有Ci=x∨D(i∈{1,2,…,m}),其中x是一文字,D是一子句,则x是S中的有用文字当且仅当子句集{x,C1-D,…,Ci-1-D,Ci+1-D,…,Cm-D}可满足。
证明 (充分性)若x不是S中的有用文字,则存在Ci∈S且Ci=x∨D,使x是Ci中关于S的冗余文字,则D是子句集S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,即D∧x∧C1∧…∧Ci-1∧Ci+1∧…∧Cm=x∧C1∧…∧Ci-1∧Ci+1∧…∧Cm。又因为Ci=x∨D,所以x∉D,于是由定理7知子句集{x,C1-D,…,Ci-1-D,Ci+1-D,…,Cm-D}不可满足,矛盾。
(必要性)假设子句集{x,C1-D,…,Ci-1-D,Ci+1-D,…,Cm-D}不可满足,由定理7知D是子句集S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,则x不是S中的有用文字,矛盾。
定理15 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,有Ci=x∨Di(i∈{1,2,…,m}),其中x是一文字,Di是一子句,且Di中不含互补文字,则x是S中的无用文字当且仅当子句集{x,C1,…,Ci-1,Ci+1,…,Cm}∪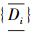 不可满足。
不可满足。
证明 若x是S中的无用文字,则一定存在Ci∈S且Ci=x∨Di,使x是Ci中关于S的冗余文字,由定理1.6知x是Ci中关于S的冗余文字当且仅当Di是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,于是再由定理4知Di是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句当且仅当子句集{x,C1,…,Ci-1,Ci+1,…,Cm}∪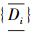 不可满足。
不可满足。
定理16 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,有Ci=x∨Di(i∈{1,…,m}),其中x是一文字,Di是一子句,且Di中不含互补文字,则x是S中的必需文字当且仅当子句集{x,C1,…,Ci-1,Ci+1,…,Cm}∪{Di}可满足。
证明 (充分性)若x不是S中的必需文字,则存在Ci∈S且Ci=x∨Di,使x是Ci中关于S的冗余文字,则Di是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,于是由定理4知子句集{x,C1,…,Ci-1,Ci+1,…,Cm}∪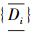 不可满足,这显然与已知矛盾。
不可满足,这显然与已知矛盾。
(必要性)假设子句集{x,C1,…,Ci-1,Ci+1,…,Cm}∪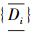 不可满足,那么由定理4知Di是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,则x不是S中的必需文字,矛盾。
不可满足,那么由定理4知Di是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,则x不是S中的必需文字,矛盾。
定理17 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果存在S中的一个子句Ci,若有Ci=x∨D(i∈{1,2,…,m}),其中x是一文字,D是一子句,则x是S中的有用文字当且仅当子句集{x,C1,…,Ci-1,Ci+1,…,Cm}∪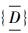 可满足。
可满足。
证明 (充分性)若x不是S中的有用文字,则存在Ci∈S且Ci=x∨D,使x是Ci中关于S的冗余文字,则D是子句集S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,于是由定理4知子句集{x,C1,…,Ci-1,Ci+1,…,Cm}∪{D}不可满足,这显然与已知矛盾。
(必要性)假设子句集{x,C1,…,Ci-1,Ci+1,…,Cm}∪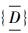 不可满足,那么由定理4知D是子句集S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,则x不是S中的有用文字,矛盾。
不可满足,那么由定理4知D是子句集S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,则x不是S中的有用文字,矛盾。
定理18 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,有Ci=x∨Di(i∈{1,2,…,m}),其中x是一文字,Di是一子句,且Di中不含互补文字,则x是S中的无用文字当且仅当子句集(S′i\{Di})|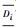 不可满足,其中Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}。
不可满足,其中Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}。
证明 由于Ci∈S且Ci=x∨Di,x是S中的无用文字,由定义知x是Ci中关于S的冗余文字,所以Di是子句集Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,再由定理4和定理8可以得出充要条件。
定理19 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果对于S中的任一子句Ci,有Ci=x∨Di(i∈{1,…,m}),其中x是一文字,Di是一子句,且Di中不含互补文字,则x是S中的必需文字当且仅当子句集(Si′\{Di})|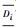 可满足,其中Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}。
可满足,其中Si′={Di,x,C1,…,Ci-1,Ci+1,…,Cm}。
证明 (充分性)由于Ci∈S,Ci=x∨Di,假设x不是S中的必需文字,由定义可以知x是Ci中关于S的冗余文字,所以Di是子句集S′i={Di,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,再由定理4和定理8可以得出子句集(Si′\{Di})|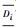 不可满足,矛盾。
不可满足,矛盾。
(必要性)假设(S′i\{Di})|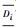 不可满足由定理4和定理8可知x一定是Ci关于S的冗余文字,这与x是S中的必需文字矛盾。
不可满足由定理4和定理8可知x一定是Ci关于S的冗余文字,这与x是S中的必需文字矛盾。
定理20 设S={C1,C2,…,Cm}是命题逻辑中的子句集,如果存在S中的一个子句Ci,若有Ci=x∨D(i∈{1,2,…,m}),其中x是一文字,D是一子句,则x是S中的有用文字当且仅当子句集(S′\{D})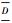 可满足,其中S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}。
可满足,其中S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}。
证明 (充分性)由于Ci∈S,Ci=x∨D,假设x不是S中的有用文字,由定义知x一定是Ci中关于S的冗余文字,所以D是子句集S′={D,x,C1,…,Ci-1,Ci+1,…,Cm}中的冗余子句,再由定理4和定理8可以得出子句集(S′\{D})|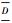 不可满足,矛盾。
不可满足,矛盾。
(必要性)假设(S′\D})|D不可满足由定理4和定理8可知x一定是Ci中关于S的冗余文字,这与x是S中的有用文字矛盾。
4 结束语本文主要研究命题逻辑的子句集中必需文字、有用文字和无用文字的特征,讨论它们相应的等价条件。然后运用冗余文字和冗余子句的知识,得到必需文字、有用文字和无用文字与子句集可满足性的判定方法。该方法丰富了命题逻辑的子句集中文字的分类方法,得到子句集中文字特征的判定方法,为命题逻辑公式的化简奠定了理论基础。但是目前的冗余文字判定方法对子句集中文字属性的判断处理过程比较复杂,下一步将继续深入研究子句集的分类,为命题逻辑中子句集的化简和高效的归结自动推理提供理论支撑。
| [1] | LIBERATORE P. Redundancy in logic I: CNF propositional formulae[J]. Artificial Intelligence, 2005, 163(2): 203-232. |
| [2] | LIBERATORE P. Redundancy in logic Ⅱ: 2CNF and Horn propositional formulae[J]. Artificial Intelligence, 2008, 172(2/3): 265-299. |
| [3] | BOUFKHAD Y, ROUSSEL O. Redundancy in random SAT formulas[C]// Proceedings of the 7th National Conference on Artificial Intelligence.[S.l.], 2000: 273-278. |
| [4] | FOURDRINOY O, GRÉGOIRE É, MAZURE B, et al. Eliminating redundant clauses in sat instances[M]// Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems. Berlin/Heidelberg: Springer, 2007: 71-83. |
| [5] | KULLMANN O. Constraint satisfaction problems in clausal form Ⅱ: Minimal unsatisability and conict structure[J]. Fundamenta Informaticae, 2011, 109(1): 83-119. |
| [6] | MANTHEY N. Coprocessor 2.0—A flexible CNF simplifier[J]. Theory and Applications of Satisfiability Testing-SAT, 2012, 7317: 436-441. |
| [7] | BELOV A, JANOTA M, LYNCE I, et al. On computing minimal equivalent subformulas[J]. Principles and Practice of Constraint Programming, 2012, 7514: 158-174. |
| [8] | 张建. 逻辑公式的可满足性判定——方法、工具及应用[M]. 北京: 科学出版社, 2000: 22-30. |
| [9] | 许有军. 基于扩展规则的若干SAT问题研究[D]. 长春: 吉林大学, 2011: 15-28. XU Youjun. Research on several SAT issues based on extension rule[D]. Changchun, China: Jilin University, 2011 : 15-28. |
| [10] | CHANG C L, LEE R C T. Symbolic logic and mechanical theorem proving[M]. New York: Academic Press, 1973: 19-73, 22-25. |
| [11] | LIU Yi, JIA Hairui, XU Yang. Determination of 3-Ary α-resolution in lattice-valued propositional logic LP(X)[J]. International Journal of Computational Intelligence Systems, 2013, 6(5): 943-953. |
| [12] | 翟翠红, 秦克云. 命题逻辑公式中的冗余子句及冗余文字[J]. 计算机科学, 2013, 40(5): 48-50. ZHAI Cuihong, QIN Keyun. Redundancy clause and redundancy literal of propositional logic[J]. Computer Science, 2013, 40(5): 48-50. |
| [13] | 唐世辉. 命题逻辑中子句集的冗余性研究[D].成都: 西南交通大学, 2014: 30-35. TANG Shihui. Research redundancy of set of clauses in propositional logic[D]. Chengdu, China: Southwest Jiaotong University, 2014: 30-35. |
| [14] | 王国俊. 数理逻辑引论与归结原理[M]. 北京: 科学出版社, 2006: 16-25. WANG Guojun. Introduction to mathematical logic and resolution principle[M]. Beijing: Science Press, 2006: 16-25. |
| [15] | MUGGLETON S. Inductive logic programming[J]. New Generation Computing, 1991, 8(4): 295-318. |



