2. 南京理工大学 计算机科学与技术学院, 江苏 南京 210094
2. School of Computer Science and Technology, Nanjing University of Science and Technology, Nanjing 210094, China
聚类[1, 2]是数据挖掘领域中十分重要的数据分析技术。具体来说,聚类就是将给定的数据集划分成互不相交的非空子集的过程。由于初始条件和聚类准则的不唯一性,使得各种各样的聚类算法应运而生。根据算法形成方式的不同,可以将其分为2大类:基于划分的聚类算法和基于层次的聚类算法[3]。基于划分的聚类算法也可以称为分割聚类算法,它的主要特点是在对数据集进行分类之前,需要事先确定聚类个数,然后将数据集划分到确定好的各类别中。根据划分过程中数据点类别归属的明确性,又可将分割聚类分为硬聚类和模糊聚类[4]。
硬聚类中数据点的类别归属是明确的。每个数据点对各类别的隶属度取0或1,即一个数据点必须属于某一类别且只能属于该类别。硬聚类的数学定义描述如下:设给定的数据集为X={x1,x2,…,xn}∈Rn×d,xi(i=1,2,…,n)表示第i个数据点。预先确定将X划分为k个子集C={C1,C2,…,Ck}
(k≤n),则Ci满足如下条件:1)
Ci≠∅,(i=1,2,
…,k),即每一子集至少含有一个数据点;2)Ci∩Cj=∅,(1≤i≠j≤k),即每个数据点只能属于一个子集;
3)∪i=1kC
i=X,即每个数据点必须归属于某一子集。数据点xj(j=1,2,…,n)对子集Ci (i=1,2,…,k)的隶属关系可用隶属函数uij表示,当uij= 1时,
xj∈Ci,当uij= 0时,xj∉Ci,其中隶属函数uij∈{0,1}且满足 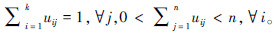 硬聚类的代表算法有K-means算法[5]和Ncuts(normalized cuts)算法[6]。二者都是致力于得到使目标函数达到最值的最优聚类。K-means算法取误差平方和函数作为目标函数,对初始聚类中心和异常点较为敏感,且面对非凸数据集易陷入局部最优。Ncuts算法取规范割函数为目标函数,将数据集的聚类问题转化为空间中带权无向图的最优划分问题。Ncuts算法可以聚类任意形状的数据,但大数据聚类问题对其相似性矩阵的存储和特征向量的计算都是种挑战。
硬聚类的代表算法有K-means算法[5]和Ncuts(normalized cuts)算法[6]。二者都是致力于得到使目标函数达到最值的最优聚类。K-means算法取误差平方和函数作为目标函数,对初始聚类中心和异常点较为敏感,且面对非凸数据集易陷入局部最优。Ncuts算法取规范割函数为目标函数,将数据集的聚类问题转化为空间中带权无向图的最优划分问题。Ncuts算法可以聚类任意形状的数据,但大数据聚类问题对其相似性矩阵的存储和特征向量的计算都是种挑战。
在模糊聚类中,数据点的类别归属是不明确的,一个数据点可以属于所有类别。模糊聚类隶属度的取值由硬聚类中只能取0或1变为可以取[0,1]的任意值,该值用来表示每个数据点属于各个类别的可能性,仍然满足任意数据点对所有类别的隶属度之和为1。代表性的模糊聚类算法有FCM算法[7]和PCM(possibilitic C means)算法[8]。FCM算法利用数据点对每一类别的隶属度构成了一个隶属矩阵,然后将算法的目标函数转变为一个与隶属矩阵相关的函数,通过优化该目标函数完成聚类。为克服FCM对噪声敏感的缺点,Krishnapuram和Keller提出了PCM算法。该算法舍弃了FCM算法中每一点对各类别隶属度总和为1的约束条件,使得噪声点具有很小的隶属度值,从而增加了算法对噪声的鲁棒性。
层次聚类算法又称为树聚类算法。它的主要思想是对给定的数据集依照相似性矩阵进行层次分解,使得聚类结果可以由二叉树或系统树图来描述,即树状嵌套结构为H = {H1,H2,…,Hq},(q≤n),n为数据点的个数,当Ci∈Hm,Cj∈Hl且m>l,有Ci∈Cj或Ci∩Cj=∅对所有i成立,j≠i,m,l = 1,2,…,q。层次聚类算法又分为分裂式和凝聚式2种。
分裂式层次聚类算法采用“自顶向下”的方式进行。将数据集看作一类,根据类内最大相似性的原则将数据集逐渐细分,直到满足终止条件或每一个数据点构成一类时停止分裂,例如MONA(monothetic analysis)算法[9]和DIANA(divisive analysis)算法[9]等。
凝聚式层次聚类算法[10]采用“自底向上”的方式进行。一开始将数据集的每个数据点看作一类,然后进行一系列的合并操作,直到满足终止条件或所有数据点归为一类时停止凝聚。大部分层次聚类算法都是采用凝聚式聚类,代表性的算法有基于代表点的CURE算法[11]、基于稠密点的DBSCAN算法[12]、NBC(neighborhood based clustering)算法[13]、以及基于核心点的MulCA(multilevel core-sets based aggregation)算法[14]等。
随着信息技术的迅猛发展,数据源开始不断膨胀,数据结构也变得日渐复杂,具有类内相异、类间相似、噪声和重叠现象的数据集层出不穷,这对于计算机领域中一些易受噪声点和数据集大小影响的经典聚类算法(如K-means、Ncuts等)来说,是一种巨大的挑战。
在寻求更优的聚类算法的道路上,人们开始将其他专业领域的知识同聚类算法相结合,统计思想逐步被应用于聚类算法中。早期统计聚类方法有GMDD算法[15]和EM算法[16]等。GMDD算法将数据点和噪声点看作是由不同混合高斯分布生成的点集,利用一个增强的模型模拟估计含有噪声点的原始模型。EM算法是一种迭代算法,用于含有隐变量的概率参数模型的最大似然估计或极大后验概率估计。2004年,针对复杂的图像分割问题,Nock和Nielsen提出了统计区域合并算法(statistical region merging,SRM)[17]。具体地,该算法将像素点作为最基本的区域,把像素的3个颜色特征看做3组独立随机变量,对每一组独立随机变量,根据独立有限差分不等式得出合并的判定准则,利用像素点梯度值从小到大的排序获得合并顺序,依据合并准则和合并顺序,结合像素或区域进行迭代生长。通过控制每组独立随机变量的个数,SRM算法实现了对复杂图像中目标的快速分割和有效提取。
受SRM方法的启发,本文提出了一种基于密度的统计合并聚类算法(density-based statistical merging clustering,DSMC),该算法主要包括2个步骤:
1)根据数据点的密度信息获得合并顺序及每一数据点的k邻域。首先利用数据点的空间位置信息及多维特征信息,计算数据点之间的相似性得到相似性矩阵,确定每一数据点的k邻域。然后将稠密点与其k邻域中所有点的相似性的最小值作为数据点的密度信息,将密度从大到小的排序作为合并的顺序。
2) 按照合并顺序依次将稠密点与其k邻域中的数据点进行合并判定。将数据点的每个特征看作一组独立随机变量,根据独立有限差分不等式得出的合并判定准则判断两点是否合并。当2个数据点对其任意的特征具有相同的期望时,划分为同一类别;当2个数据点对其特征至少有一个期望显著不同时,划分为不同类别。遍历所有的稠密点,实现对数据集的分类。
相比于上述基于密度的凝聚聚类算法(如DBSCAN、NBC)DSMC算法在数据点生长合并的过程中,不仅利用了数据点的密度信息,还利用了根据统计判定准则得出的数据点每一个特征的差异性信息。因此,该算法对噪声具有更好的鲁棒性,也对不规则形状的数据集和密度不均匀的数据集具有更好的聚类效果。
1 DSM 1.1 统计模型的建立设给定的数据集为X,包含n个数据点,每个数据点含有多个特征信息,用Ω={A,B,C,…}表示特征集合,每个特征的取值范围为[Li,Ui](i= A,B,C,…)。为方便应用,对数据集X作整体移动(特征信息整体改变不影响分类),使得特征的取值范围变为[0,gi](i= A, B,C,…),其中gi = |Ui-Li|。然后,将数据点的每一个特征用Q个独立随机变量表示,每一个随机变量对应一个分布。以特征A为例,其可表示为A = (A1,A2,…,AQ),随机变量Aj (j = 1,2,…,Q)对应第j个分布。由于Q个独立随机变量和的取值应属于[0,gi](i= A,B,C,…),则每一个随机变量的取值为[0,gi/Q](i= A,B,C,…)。这样,一个数据点的特征信息就由多组独立随机变量表示。
对于给定的数据集X,假设存在具有完美聚类结果的数据集X*,那么在X*中,最优的聚类结果具有如下性质:1) 同一类别中的数据点,对于任意给定的数据特征都具有相同的期望;2) 不同的类别中的数据点,对于任意给定的数据特征至少有一个期望不同。这一性质在合并判定过程中起到非常重要的作用。
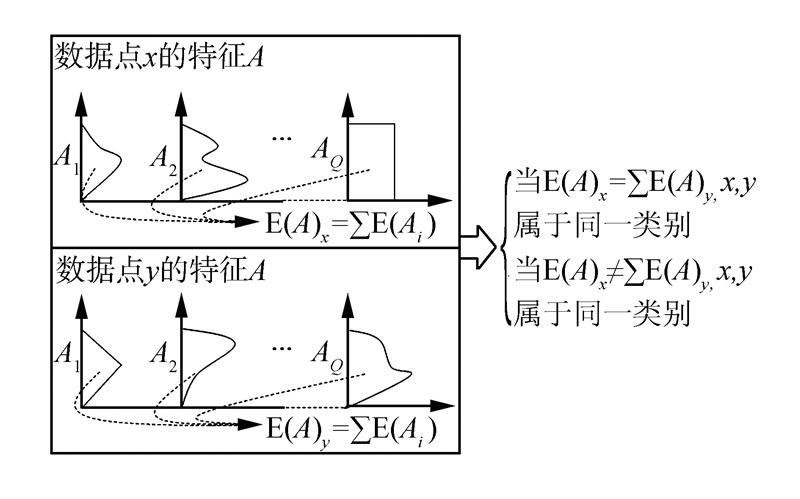 |
| 图 1 2个数据点任一特征聚类的统计说明Fig. 1 The statistical description of two data points clustering about any feature |
该统计模型对数据点及数据点特征的取样是相互独立的。对于Q个独立随机变量的分布没有特定要求,即独立不一定同分布。Q的传统取值一般为1,即数据点的每个特征只由一个随机变量表示,但是这一取值对于较小的数据集难以获得可靠的估计信息。当Q增大时,数据点的特征可以被描述的更加细致,因此,Q成为该算法的重要参数之一。调整参数Q,不仅可以改变算法的统计复杂性,还可以控制分类的精确度。将Q的取值从小调大,可以建立一个层次由粗到细的数据聚类结果。
1.2 统计合并判定DSM算法对数据点的合并由一个特定的统计合并判定准则决定。为了简单起见,先只考虑含有一个特征信息的数据集,即一个数据点用一组独立随机变量表示。在此基础上,将得到的结果扩展到具有更多的特征信息的数据集中。
为了得出统计合并判定准则,介绍定理如下:
定理1(独立有限差分不等式[18]) 设X=(X1,X2,…,Xn)是一组独立随机变量,Xk的取值范围为Ak (k = 1,2,…,n)。假设存在一个定义在∏kAk的实值函数f,当变量X与X′仅在第k个条件不同时,满足|f ()-f(X′)|≤rk,则∀τ≥0,有
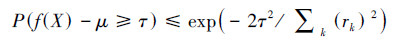
根据定理1,可以推出给定数据集X中的不同类别的绝对偏差不等式。记C为数据集X中的类别(单个数据点可作为一个类别),|C|为类别内数据点的个数,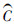 表示类别C与其他类别合并时的代表点,E(C)表示该类别相关数据点Q个独立随机变量期望和的期望。
表示类别C与其他类别合并时的代表点,E(C)表示该类别相关数据点Q个独立随机变量期望和的期望。
推论1 考虑数据集X中的类别组合(C1,C2),∀0<δ≤1,下面不等式成立的概率不超过δ:
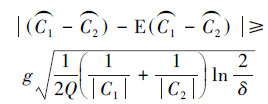
证明 已知类别C1中的数据点可由Q|C1|个独立随机变量表示,类别C2中的数据点可由Q|C2|个独立随机变量表示。 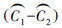 为实值函数,由于
为实值函数,由于 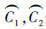 分别是C1,C2的代表点,若变动C1中的变量,rk的最大取值为g / (Q|C
1|),若变动C2中的变量,rk的最大取值为g / (Q|C2|)。
分别是C1,C2的代表点,若变动C1中的变量,rk的最大取值为g / (Q|C
1|),若变动C2中的变量,rk的最大取值为g / (Q|C2|)。
记 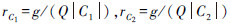 ,则
,则
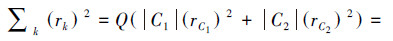
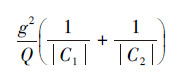
根据定理1,取 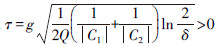 ,则
,则
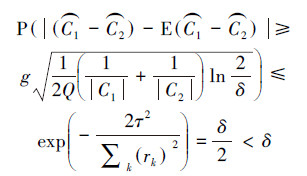
由推论1可知,当δ取值接近于零时(本文若未特别标明,δ取为1/(6|X|2),类别组合(C1,C2)满足不等式 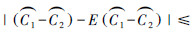 b(C1,C2)的概率接近于1,其中b(C1,C2)=
b(C1,C2)的概率接近于1,其中b(C1,C2)=
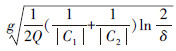 ;若(C1,C2)可以合并,说明在数据集X*中2者属于同一类别,则有
;若(C1,C2)可以合并,说明在数据集X*中2者属于同一类别,则有
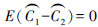 。根据这2个前提条件得到如下统计合并判定准则:
。根据这2个前提条件得到如下统计合并判定准则:
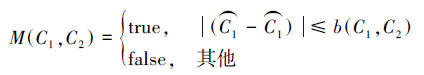
当类别组合(C1,C2)满足
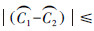 ≤b(C1,C2)时,则合并(C1,C2);反之则不然。
≤b(C1,C2)时,则合并(C1,C2);反之则不然。
将该准则扩展到具有多个特征信息的数据集中,形式如下:

建立合适的合并准则后,聚类算法的结果受合并顺序的影响。与随机选取数据点进行合并判定的算法不同,DSMC算法利用了数据点的密度信息以获得合并顺序。获取过程可叙述如下:首先,计算数据集中任意2点之间的距离度量(例如欧式距离、最大/最小距离、马氏距离等),获得度量矩阵;然后,确定每一数据点的k邻域,选取k邻域中所有点与稠密点距离度量的最大值,作为稠密点的局部密度信息;最后,根据获得的局部密度信息,将所有数据点按密度从大到小排序,得到算法的合并顺序。在整个算法过程中,基于密度的合并顺序保证了在任意2个不同的类别进行合并判定时,其自身已经完成所有可能的合并。
由上述合并顺序的获取过程可以看出,k邻域大小的选择直接影响了数据点密度的大小,进而影响了DSMC算法的合并顺序。因此,k邻域的大小也被看作是DSMC算法的一个重要参数。
在该算法中,密度的大小不仅受到k邻域的影响,也会受到距离度量f(x,y)的影响。针对不同特征的数据集,选取合适的f(x,y)可以得到更好的聚类结果。在算法中较为常见的距离度量有欧式距离,马氏距离,最大/最小值距离等。本文实验中主要应用一种距离度量,它利用数据点最大特征差异进行排序,使得d=maxy∈K(x)maxxi-yi,(i = A,B,C,…),K(x)表示点x的k邻域。随机生成含有20个点的数据集,选取k邻域大小为4,利用上述距离度量,得到DSMC算法的合并顺序如图2所示。
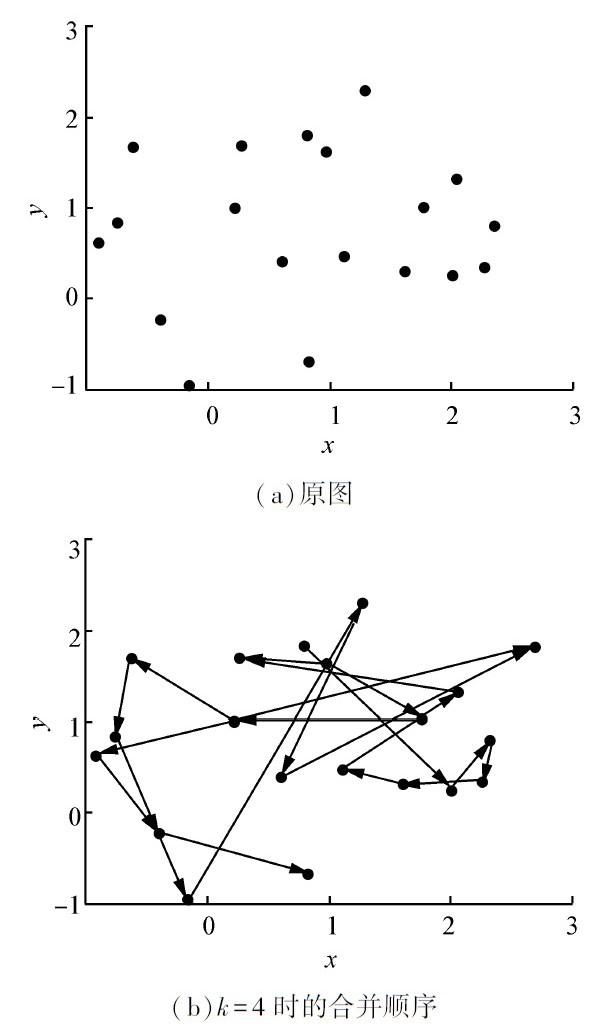 |
| 图 2 DSMC算法的合并顺序Fig. 2 Merging order of DSMC algorithm |
通过对DSMC算法的详细介绍可知,DSMC算法主要通过2个步骤实现:步骤1是根据数据点的密度信息获得合并顺序及每一数据点的k邻域;步骤2是按照合并顺序依次将稠密点与其 k邻域中的数据点进行合并判定,通过遍历所有的稠密点完成数据的聚类。其中,为更好地处理噪声点,在步骤2中只对 α比例的数据(本文默认α=0.9)进行统计判定,剩余数据点根据临近数据点的类别标号。根据这2个步骤的内容,具体说明DSMC算法的聚类过程如下。
步骤1:计算数据点的合并顺序并获得数据点的k邻域。
输入:数据集X;k邻域中数据点个数k。
1)计算数据集中任意两个点距离,存入矩阵D。
2)将矩阵D按列进行升序排列,存入矩阵D1,其第k行按升序排列,得到密度从大到小的顺序d。
3)根据顺序d确定数据点的k邻域。
输出:合并顺序d;k邻域矩阵W。
步骤2:将稠密点与其k邻域中的数据点进行合并判定,然后合并剩余点完成聚类。
输入:数据集X;合并顺序d;k邻域矩阵W。
1)对数据集中90%的数据点(稠密点)进行合并判定。
a)根据合并顺序d确定当前稠密点
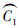 ,然后依次选定其k邻域内的点作为当前合并点
,然后依次选定其k邻域内的点作为当前合并点 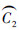 ,判断
,判断
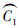
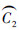 的类别归属;
的类别归属;
b)计算统计判定准则的临界值b(C1,C2)(推论1),若满足统计合并判定准则,则合并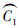
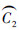 ;若不满足,则进行下一组合并判断,直到遍历完k邻域内所有的点;
;若不满足,则进行下一组合并判断,直到遍历完k邻域内所有的点;
c)重复步骤a)和b),直到遍历完数据集X中所有的稠密点。
2)对剩余的10%的数据点进行近邻合并。
a)根据合并顺序d确定当前点
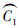 ;
;
b)判断其k邻域内点的分类情况。若有已分类的点,且其k邻域中属于该类别的点数最多,则将
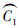 归于该类别;若没有已分类的点,则
归于该类别;若没有已分类的点,则
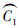 不作改变;
不作改变;
c)重复步骤a)和b),直到遍历完剩余所有的数据点 。
3)计算数据集X的分类个数nbcluster。
输出:聚类个数nbcluster。
由高斯分布随机生成一个可被分为2类的数据集X,其含40个数据点。用DSMC算法(参数k和Q取为5,15)对数据集X进行聚类,具体过程如图3所示。过程①对于给定的数据集X计算合并顺序,得到首要稠密点及其k邻域;过程②按照数据集的合并顺序,依次对稠密点和其k邻域中的点进行统计合并判定得到聚类结果;过程 ③根据临近数据点的类别对噪声点进行聚类,比较其k邻域中各类别点的个数,将它归为点数最多类别。
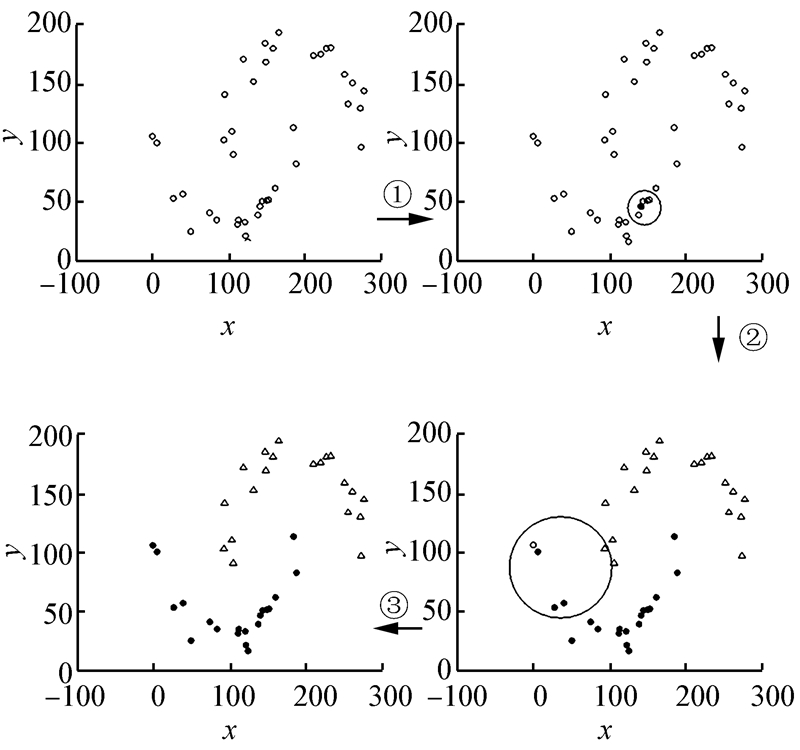 |
| 图 3 DSMC算法的聚类过程Fig. 3 Clustering process of DSMC algorithm |
由上述聚类过程可知,DSMC算法的计算量主要集中于2个步骤:
1)构建数据点的距离度量矩阵;
2)统计合并判定时对稠密点及其k邻域的迭代。
对于步骤1),给定含有n个点的数据集,距离度量矩阵的计算复杂度为O(n2);对于步骤2),遍历数据集中所有稠密点,将当前稠密点依次与其k邻域中的点进行统计合并判定,由于k邻域内点的最大迭代次数为k,因此,步骤2)的计算复杂度为O(kn)。一般地,k的取值远小于n,则DSMC算法的计算复杂度可近似于距离度量矩阵的计算复杂度O(n2)。
3 实验比较与评价将DSMC算法同3种经典聚类算法作比较,它们分别是通过聚类中心实现的K-means算法、基于图论的Ncuts算法和基于密度的DBSCAN算法。针对具有不同形状,不同重叠程度和不同噪声点数的人工数据集以及部分真实数据集进行实验。进一步地,对本
文提出的DSMC算法的参数选择进行了实验分析。
由于不同的算法具有不同的参数,在3.1~3.5节的实验中,实验参数设置如下:1)K-means和Ncuts算法:只有1个参数,即想要达到的聚类个数。一般地,实验中将数据集真实的聚类个数取为参数值。
2)DBSCAN算法:共有2个参数,一个是点的邻域半径r,一个是邻域内点的个数阈值m。在实验中,m一般取10左右的数,邻域半径r则根据数据集的直径做决定。
3)DSMC算法:共有2个参数,分别是邻域内点的个数k和划分尺度参数Q。参数k的取值一般根据数据集中数据点的总个数确定。一般初始值取10左右。对于该方法特有的参数Q,它控制了算法对数据集的划分细度,即当Q较小时,数据集划分细度小,聚类个数少;当Q较大时,数据集划分细度大,聚类个数多。由于参数Q是一个特征独立随机变量的个数,因此其取值范围为正整数,实验中具体取值根据数据集分类需求进行调整,默认初始值为1。
3.1 形状不同的人工数据集实验将4种聚类算法(K-means,Ncuts,DBSCAN,DSMC)分别应用于4种不同形状的人工数据集上。它们通过不同类型的高斯分布随机生成,样本点的个数从左到右第1行分别为600、900;第2行分别为660(包含60个随机噪声点),1 100(包含100个随机噪声点)。
对任意形状的数据集都有良好聚类效果的算法才能称之为好的聚类算法。由图4可以看出,K-means和Ncuts算法并不能很好的聚类非凸数据集,而DBSCAN算法(参数m和r从左到右第1行为8,0.4;7,0.7;第2行为100,48;15,0.4)和本文提出的DSMC算法(参数k和Q从左到右第1行为6,200;8,1;第2行为8,1;8,6)对任意形状数据集的聚类效果都很令人满意,但对于较为稀疏的数据点的聚类,DSMC算法相对更优。
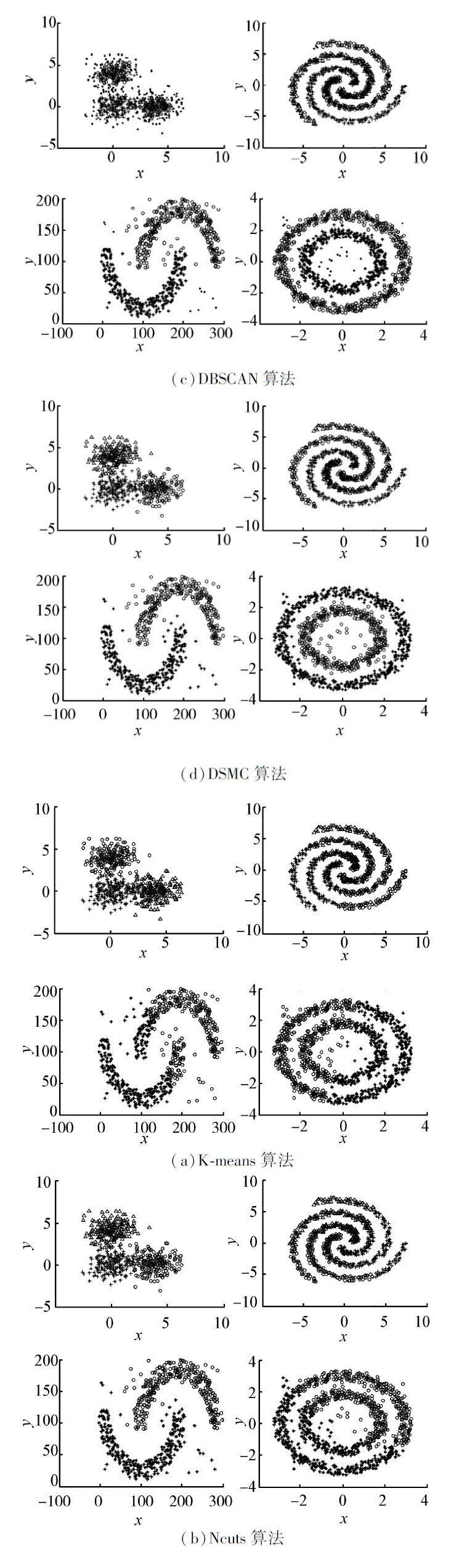 |
| 图 4 算法对不同形状数据集的分类结果比较Fig. 4 Comparison of classification results of algorithms for different shape data sets |
对数据重叠的鲁棒性也是判断聚类算法好坏的标准之一。本节中,通过对重叠程度逐渐增大的2类不同形状的人工数据集进行实验,比较4种聚类算法对数据重叠的鲁棒性。其中,团状数据集含有600个数据点;环状数据集含有1 000个数据点。
从图5的实验结果可以看出,对于团状数据集,K-means、Ncuts和DSMC(参数k和Q自上而下依次取为6,200;6,160)算法都能够很好的处理重叠问题,而DBSCAN算法(参数 m和r自上而下依次取为8,0.4;10,0.6)虽然对一般的团状数据集聚类效果显著,但随着数据集重叠程度的逐渐增大,聚类效果也开始变差。对于环状数据集,像K-means、Ncuts这种无法很好的聚类非凸数据集的算法,对于重叠的环状数据集一样效果不好;而DBSCAN算法(参数m和r自上而下依次取为15,0.4;10,0.5)对环状数据集的聚类类似于团状数据集,对重叠度较高的数据集不能很好地聚类;本文提出的DSMC算法(参数k和Q自上而下依次取为7,15;7,75)对于高重叠度的环状数据集虽然没有得到完美的聚类结果,但将内环与外环数据归为2类的结果基本令人满意。相比其他3种聚类算法而言,DSMC算法对重叠的鲁棒性较好。
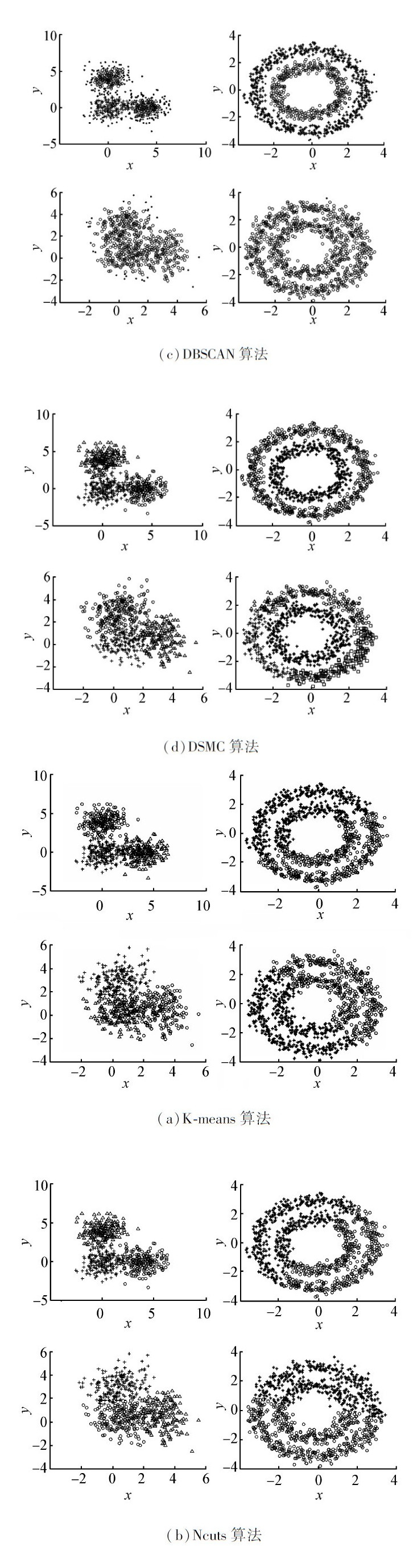 |
| 图 5 对不同重叠程度的团状和环状数据集的分类结果比较Fig. 5 Comparison of classification results on different degree of overlap between group and cyclicdata sets |
随着数据源含有噪声现象的增多,算法对噪声的处理效果也越来越受到人们的关注。为检验本文提出的DSMC算法对含有噪声的数据集的聚类效果,对逐渐增加噪声点的两类非凸数据集进行实验。其中,第1个数据集含有400个数据点,第2个数据集含有1 000个数据点,自上而下对2个数据集分别加入100、200、300个噪声点。
图6的实验结果说明,DSMC算法(参数k和Q自上而下依次取为8,1;16,70;8,70;8,6;7,8;9,20)对数据中的噪声具有良好的鲁棒性。
 |
| 图 6 DSMC算法对逐渐增加噪声点的数据集聚类结果Fig. 6 Clustering results over the noisy data sets of DSMC algorithm |
为进一步说明DSMC算法的有效性,将该算法应用于混合形状的人工数据集(凸状和非凸状混合),其中,该混合数据集含有1 520个数据点,包括320个噪声点。图7表明,DSMC算法(参数k和Q为10,100)对这种密度不均匀的混合数据集也能很好地聚类。
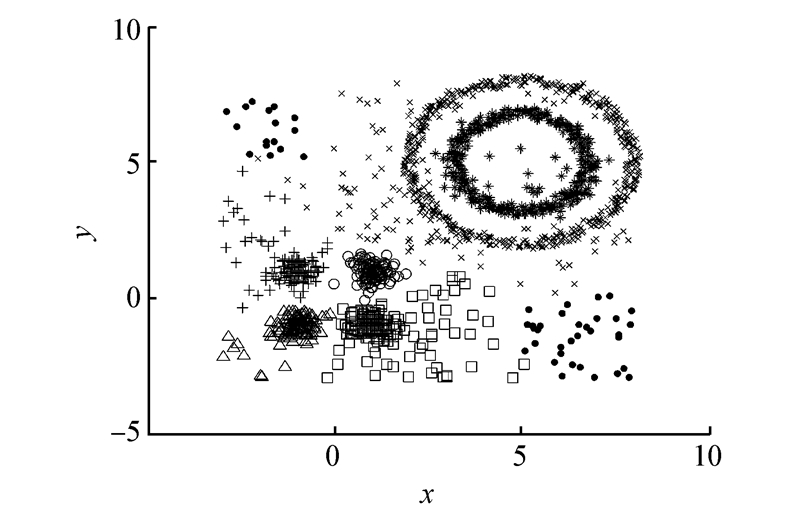 |
| 图 7 DSMC算法对混合数据集的聚类结果Fig. 7 Clustering results of DSMC algorithm for mixed data set |
基于对人工数据集良好的聚类效果,本节继续应用DSMC算法对真实数据集进行聚类,并同K-means、Ncuts、DBSCAN算法的聚类结果作比较。实验对象选自UCI数据库 (http://archive.ics.uci.edu/ml/,加州大学欧文分校提出的用于机器学习的数据库,目前包含 223 个数据集)中的4个不同的数据集,分别是iris,wine,seeds,glass。4个数据集的基本特征如表1所示。
| 数据集 | 样本点数 | 特征个数 | 类别数 |
| iris | 150 | 4 | 3 |
| wine | 178 | 13 | 3 |
| seeds | 210 | 7 | 3 |
| glass | 214 | 10 | 6 |
在实验中,DSMC算法中的参数k和Q自上而下依次取为6,140;8,7;6,180;6,70. DBSCAN算法中的参数 m和r自上而下依次取为11,0.5;7,51;5,1.1;15,8. 由表2可知,DSMC算法对iris、seeds和glass的聚类效果要好于其他3种聚类算法;对wine的聚类虽然不如Ncuts算法,但结果基本令人满意,说明DSMC算法对真实数据集也有良好的聚类结果。
| 数据集 | Accuracy/% | |||
| DSMC | K-means | Ncuts | DBSCAN | |
| iris | 97.33 | 89.33 | 81.33 | 75.33 |
| wine | 72.47 | 70.22 | 79.21 | 53.37 |
| seeds | 90.48 | 89.05 | 85.24 | 89.52 |
| glass | 77.57 | 72.90 | 46.26 | 64.95 |
DSMC算法中涉及到的2个重要参数分别是独立随机变量的个数Q和邻域内数据点的个数k。
独立随机变量的个数Q控制了算法的分类精确度。在固定k邻域的情况下,随着Q取值的逐渐增大,聚类个数也会随之增多。图8显示了在固定k的情况下,不同的Q值对环状人工数据集和真实数据集iris产生的不同聚类效果。对于环状人工数据集,固定k=8,Q取1~16时数据集得到完美聚类,随着Q值的增大,分类更加细化,聚类个数逐渐增多。对于真实数据集iris,固定k=6,Q取1~52 时数据集后2类不能被分开,分类正确率低;当Q增大至53~252时,后两类被分开,分类正确率增至最大;当Q取252以上,类别数增加,分类正确率下降。
 |
| 图 8 固定k值时,不同Q的聚类结果Fig. 8 Clustering results of different Q with a fixed k value |
邻域内数据点的个数k决定了算法的合并顺序,在固定Q值的情况下,随着k邻域的逐渐增大,聚类个数会随之减少。图9显示了在固定Q的情况下,将k逐渐增大时的两个数据集聚类效果。对于环状人工数据集,固定Q=1,当k取1~7时,分类个数过多,聚类结果并不理想;当k取8~18时,聚类结果稳定且保持较高水平;当k取19以上时,数据集被聚为一类,结果不理想。对于真实数据集iris,同人工数据集类似,当k取53~251时,可获得稳定的高水平聚类结果。
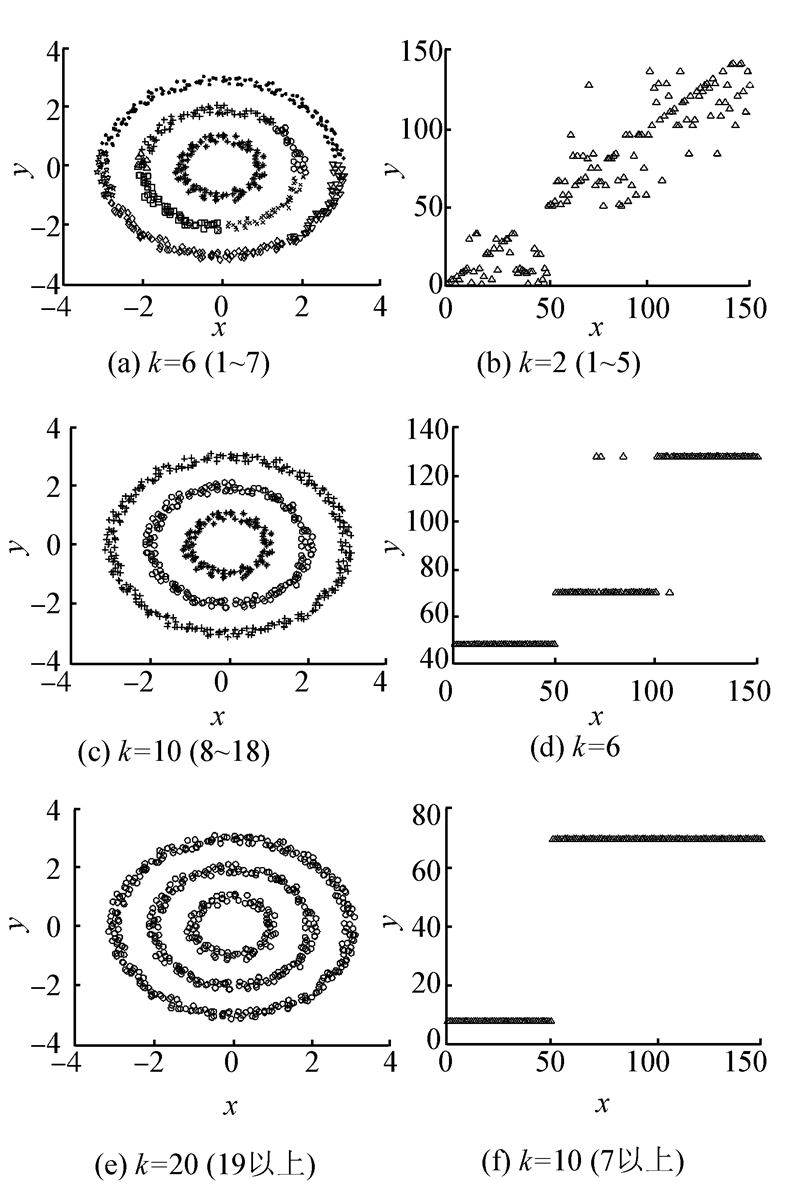 |
| 图 9 固定Q值时,不同k的聚类结果Fig. 9 Clustering results of different k with a fixed Q value |
随着信息技术水平的不断提高,具有噪声和重叠现象的数据源越来越多,仅限于计算机领域的聚类方法不能很好地处理该问题。为此,本文提出了一种同统计思想相结合的快速聚类算法—DSMC算法,它使用了一个简单的合并顺序和统计判定准则,将数据点的每一个特征看作一组独立随机变量,根据独立有限差分不等式得出统计合并判定准则,同时,结合数据点的密度信息,把密度从大到小的排序作为凝聚过程中的合并顺序,进而实现各类数据点的统计合并。对人工数据集和真实数据集测试的实验结果表明,DSMC算法对于非凸状、重叠和加入噪声的数据集都有良好的聚类效果。
在后续的研究工作中,将进一步推广DSMC算法的应用范围,使其能够快速、高效地处理大数据、在线数据等多种型态的复杂聚类问题。
| [1] | XU Rui, WUNSCHII D. Survey of clustering algorithms[J]. IEEE Transactions on Neural Networks, 2005, 16(3):645-678. |
| [2] | JAIN A K, MURTY M N, FLYNN P J. Data clustering:a review[J]. Acm Computing Surveys, 1999, 31(2):264-323. |
| [3] | MURTAGH F, CONTRERAS P. Algorithms for hierarchical clustering:an overview[J]. Wiley Interdisciplinary Reviews:Data Mining and Knowledge Discovery, 2012, 2(1):86-97. |
| [4] | TSENG L Y, YANG S B. A genetic approach to the automatic clustering problem[J]. Pattern Recognition, 2001, 34(2):415-424. |
| [5] | FORGY E W. Cluster analysis of multivariate data:efficiency versus interpretability of classifications[J]. Biometrics, 1965, 21:768-769. |
| [6] | SHI J, MALIK J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8):888-905. |
| [7] | BEZDEK J C, EHRLICH R, FULL W. FCM:The fuzzy c-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2-3):191-203. |
| [8] | KRISHNAPURAM R, KELLER J M. A possibilistic approach to clustering[J]. IEEE Transactions on Fuzzy Systems, 1993, 1(2):98-110. |
| [9] | ALPERT C J, KAHNG A B. Recent directions in netlist partitioning:a survey[J]. Integration, the VLSI Journal, 1995, 19(1):1-81. |
| [10] | ACKERMANN M R, BLÖMER J, KUNTZE D, et al. Analysis of agglomerative clustering[J]. Algorithmica, 2014, 69(1):184-215. |
| [11] | GUHA S, RASTOGI R, SHIM K. Cure:an efficient clustering algorithm for large databases[J]. Information Systems, 2001, 26(1):35-58. |
| [12] | ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of 2nd International Conference on Knowledge Discovery and Data Mining. Portland, USA, 1996:226-231. |
| [13] | ZHOU Shuigeng, ZHAO Yue, GUAN Jihong, et al. A neighborhood-based clustering algorithm[M]//Advances in Knowledge Discovery and Data Mining. Berlin/Heidelberg:Springer, 2005:361-371. |
| [14] | 马儒宁, 王秀丽, 丁军娣. 多层核心集凝聚算法[J]. 软件学报, 2013, 24(3):490-506. MA Runing, WANG Xiuli, DING Jundi. Multilevel core-sets based aggregation clustering algorithm[J]. Journal of Software, 2013, 24(3):490-506. |
| [15] | ZHUANG Xuan, HUANG Yan, PALANIAPPAN K, et al. Gaussian mixture density modeling, decomposition, and applications[J]. IEEE Transactions on Image Processing, 1996, 5(9):1293-1302. |
| [16] | MACLACHLAN G J, KRISHNAN T. The EM algorithm and extensions[J]. Series in Probability & Statistics, 1997, 15(1):154-156. |
| [17] | NOCK R, NIELSEN F. Statistical region merging[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(11):1452-1458. |
| [18] | HABIB M, MCDIARMID C, RAMIREZ-ALFONSIN J, et al. Probabilistic methods for algorithmic discrete mathematics[M]. Berlin:Springer-Verlag, 1998:1-54. |



