移动机器人路径规划主要解决3个问题:1)使机器人能从初始点运动到目标点;2)用一定的算法使机器人能绕开障碍物,并且经过某些必须经过的点完成相应的作业任务;3)在完成以上任务的前提下,尽量优化机器人运行轨迹。移动机器人路径规划技术从移动机器人路径规划的具体算法与策略可概括为以下4类[1]:模版匹配路径规划技术、人工势场路径规划技术、地图构建路径规划技术和人工智能路径规划技术。
模版匹配技术在环境确定情况下,有较好的应用效果[2, 3, 4, 5]。人工势场路径规划将机器人在环境中的运动视为一种机器人在虚拟的人工受力场中的运动。障碍物对机器人产生斥力,目标点对机器人产生引力,引力和斥力的合力作为机器人的控制力,从而控制机器人避开障碍物而到达目标位置[6, 7, 8, 9, 10, 11, 12]。地图构建分为路标法和栅格法,路标法是构造一幅由标志点和连接边线组成的机器人可行路径图,如可视线方法、切线图方法、Voronoi图方法和概率图展开法等[13]。计算智能路径规划将生物启发的计算方法应用于移动机器人的路径规划中,如人工神经网络、进化计算、蚁群算法生物地理优化算法等[14]。但上述方法尤其是计算智能方法在复杂环境下都缺乏效率,结果也不够准确。本文针对一类复杂环境下的机器人路径规划问题,提出基于改进的生物地理学优化方法(biogeography-based optimization,BBO),以期更有效地解决该类问题。
1 有效顶点栅格环境栅格法是将环境离散化为二维(或三维)的基本单元栅格,栅格大小决定了离散化环境的分辨率,通过对这些栅格的标示来完成对机器人环境的建模,若为了节约存储空间可采用四叉树等方法进行建模,也可以从方便访问的角度出发建立逐点扫描的二维环境,最后利用搜索算法得到规划路径。这种方法因离散化的建模思想极其符合计算机的存储运算特点而得到了广泛的应用。基本栅格法包括4个步骤:1)栅格化二维平面;2)障碍物膨胀;3)标记障碍物;4)自由栅格之间的连接信息。这种方法存在以下缺点:
1) 栅格在被选入路径后需要加入禁忌表,即该栅格不能再次被选入路径中,这样当遇到一些U型槽等复杂环境会迅速生成有效的路径;
2) 自由栅格大部分都不是有效栅格,路径规划结果的信息仅包含障碍物顶点附近的部分栅格;
3) 分辨率大小难以确定。分辨率过高,增加搜索算法的运算量;分辨率过小会导致路径规划结果粗糙,在极端情况下会造成本来分开的障碍物连通,最终得不到有效的路径。
本文针对基本栅格法的以上3方面缺点,引入了一种更为有效的方法——基于有效定点的栅格编码法。该方法充分借鉴了可视图法和基本栅格法的特点而提出的方法,有效地解决了基本栅格法因分辨率而增加额外运算规模,搜索规模只与有效顶点个数,即障碍物个数及其轮廓复杂度有关系。该方法从模型上解决了U型槽等障碍物模型机器人路径规划导致的算法陷入局部收敛问题。
在m×n的栅格环境中,定义g(i,j)为{g(i,j)|i∈[1,m-1],j∈[1,n-1],i∈N,j∈N}。若栅格g(i,j),g(i,i+1),g (i+1,j),g(i+1,j+1) 4个栅格中有且只有一个障碍物栅格gob(xob,yob),那么这个4个栅格中必存在一个有效顶点gv(xv,yv),gob与gv同时满足以下2个条件:


以图1为例,按照有效顶点法将产生31个有效顶点加入到有效顶点列表S,遍历这31个有效顶点并删除重复的顶点,最后如图1所示10×10的栅格地图描述为27个有效顶点。在路径规划之前,需要将起始顶点和目的顶点加入到有效顶点列表。
 |
| 图 1 基于有效顶点的栅格示意图Fig. 1 Schematic diagram of grids based on effective vertex |
定义Availablei=∅表示,顶点si∈S的直线可达顶点集合。对于每个顶点sj∈S且i≠j若直线可达检测通过,则向Availablei添加sj,并记录dij=dji= 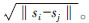
生物地理学是一门研究物种生存的自然学科,物种种群分布的地域(栖息地)各不相同。每个栖息地的生活环境各不相同,而且每个物种根据自身的生活条件也各不相同,所以对每个栖息地的适应程度也不相同,因此就有了物种的各式各样的分布、迁移和灭绝等现象。每个栖息地的适应度指数(habitat suitability index,HSI)的高低根据该栖息地的多种因素称为适应度指数变量(suitability index variable,SIV)相关,如种群类别、降雨量、地质状况、植被和气候等。如果该栖息地的适应度指数较高,那么有以下结果:物种必然呈现多样性,即物种数量大,但每个栖息地容纳物种的数量是有限度的,栖息地会因为物种众多而导致资源匮乏,适应度下降导致了物种选择离开栖息地;进入该栖息地的物种数量小于迁出该栖息地的物种数量;若栖息地的适应度指数较低,那么物种多样性减少,即物种数量稀少,但是由于物种较少,导致物种选择迁入到该栖息地的数量高于迁出该栖息地的物种。任何一个栖息地的环境状况都有一定概率发生变异,导致HIS发生改变。本文提出了基于生物地理优化的旅行商问题求解算法 [15]。
2.1 适应度指数变量SIV与机器人路径的关系设有m个岛屿,那么第i个岛屿的SIVi=(SIVi1,SIVi2,…,SIVin),对于每一个SIVij有
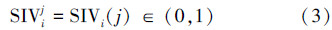
另外,生成第i个岛屿所代表的路径列表Pathi=∅,令Vs加入到Pathi中,设当前路径顶点列表Pathi有j个顶点,那么第j个顶点sj的可直线到达列表Availablei,定义集合Mi=Availablei-Pathi,定义n为Mi的个数,那么添加顶点sj+1到Pathi的队尾直到目的地顶点Vt添加到Pathi。sj+1选取方法如式(4)所示。

SIVi需要包含的变量个数需要达到N-1(N为有效顶点列表S的个数)才能够保证机器人路径生成的绝对安全。
2.2 BBO的迁移操作对于每一个SIVij,表示岛屿i的第j个适应度指数变量是否被从其他岛屿的SIVkj迁入所取代的判定:随机数rand(0,1)<λi是否成立,若成立则SIVij将被迁入变量所取代;不成立则不执行迁入操作。
迁入操作描述如下,根据每个岛屿的迁出率μi进行贪婪算法选择岛屿k,迁出操作将SIVkj迁入到SIVij,如式(5)所示。

设有M个岛屿,根据2.1描述的如何将SIV转换为路径列表Path,计算每个岛屿的所代表的路径的长度 D={D1,D2,…,Dm-1,Dm},Di越小的代表越高的HIS,所以按照Di的大小由小到大将集合D排序,排序索引可以表示为 Index={I1,I2,…,IM-1,IM},Ii表示M个Di由小到大排序的岛屿i在排序的中的位置。那么岛屿i的物种数Si可表示为

生物地理学认为栖息地的物种数量过大和过小都将导致栖息地的SIV变异率较高。定义岛屿i的变异率mi:
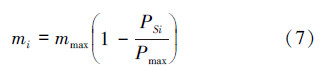
基于生物地理学的路径规划算法流程下:
1)初始化最大循环次数N; 初始化BBO的各个参数:岛屿数 M,最大变异率mmax;最大物种数Smax=M-1,最大迁出率E=1,最大嵌入率I=1;初始化每个岛屿i的SIV,SIVij= rand(0,1);
2)计算每个岛屿的路径D,并根据Di确定Si,以及PSi;保存最小路径信息和最小路径值到Dmin;
3)初始化迭代次数nc=0;
4)执行迁移操作;
5)是否执行变异操作,若不执行则跳过;
6)计算每个岛屿的路径D,并根据Di确定Si,以及PSi;计算当前代数最小路径Dminnc,若Dminnc<Dmin,则Dminnc=Dmin,保存最小路径信息;
7)nc<N是否成立,若成立,则nc=nc+1,跳到4);若不成立,则跳到7);
8)输出最短路径值和最短路径信息。
2.5 算法的改进 2.5.1 精英策略由2.3可知,mi为岛屿i的变异率,那么当i=Index(1)时,将得到最大的变异率,也就是说:路径最短的岛屿具有很高的变异率。这一结果将可能导致算法的进化出现退化。因此,精英岛屿具有变异率为0的特性。设算法有n个精英岛屿,那么设置方法如下:
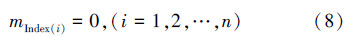
在算法步骤上,只需要将算法流程中所述的算法步骤的2)和6)分别在最末加入式(8)。
2.5.2降维根据2.1描述可以看出,SIVi需要包含的变量个数需要达到N-1(N为有效顶点列表S的个数),即岛屿的变量需要达到和有效顶点数相同(或在单项搜索的时候少1个变量,双向搜索的时候少2个变量)才能够保证机器人路径生成的绝对稳定。但一般情况下,路径规划的结果只包含整个有效顶点结合中少数个顶点。这说明,若不改进算法,算法将会是一个维数巨大的计算,而且是不必要的大维度计算。
本文尝试提出了一种降维机制描述如下:
对于在t=0时,有效顶点集合S内共有X个顶点,那么所有岛屿的SIV0的维数Y=X-2;按照2.1方法生成完整的路径,记录第i个岛屿的正向有效的SIV个数xi,和反向有效的 SIV个数yi。在t时刻,定义
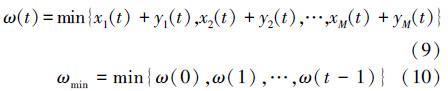
t时刻所有岛屿的SIV的维数:
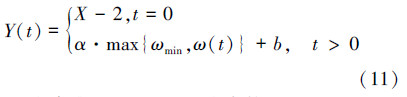
实验加载30×30环境模型路径起始点坐标为(0,0),目的地坐标为(29,29)。
1)BBO算法岛屿总数M设为30,最大变异率mmax设为0.4。算法1为有精英岛屿的BBO算法,算法2为无精英岛屿的BBO算法。2个算法各运行30次,仿真迭代趋势图,规划结果统计图,规划时间消耗统计图分别如图2~4所示。
 |
| 图 2 精英岛屿对算法迭代的影响趋势Fig. 2 Influence of the elite island on algorithm iteration |
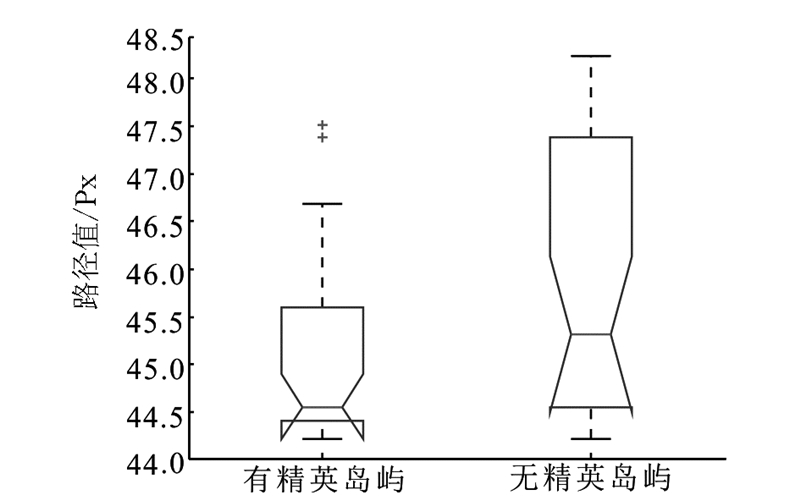 |
| 图 3 精英岛屿对算法结果的影响统计Fig. 3 Statistics of the influence of the elite island on results of algorithm |
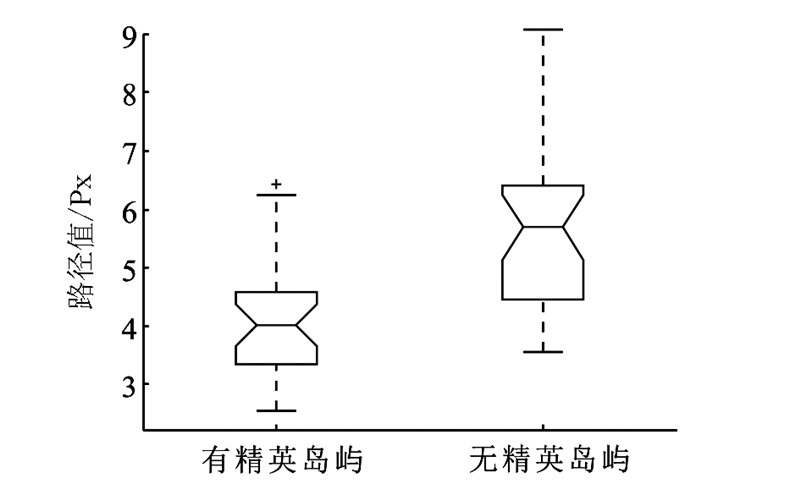 |
| 图 4 精英岛屿对算法时效的影响统计Fig. 4 Statistics of influence of the elite island on algorithm effectiveness |
从规划结果统计来看,有精英岛屿具有更高的稳定性,标准差为0.941 9而无精英岛屿为1.384 3;有精英岛屿具有更好求解最小路径能力,误差率为2.59%,而无精英岛屿为4.15%。从规划时间统计来看,有精英岛屿的BBO算法具有更小的时间消耗,节省时间平均约1.512 1 s。
2)设BBO算法岛屿总数M设为30,最大变异率mmax设为0.4。算法1为有降维机制的BBO算法,算法2为无降维机制的BBO算法。2个算法各运行30次,仿真迭代趋势图,规划结果统计图,规划时间消耗统计图分别如图5~7所示。
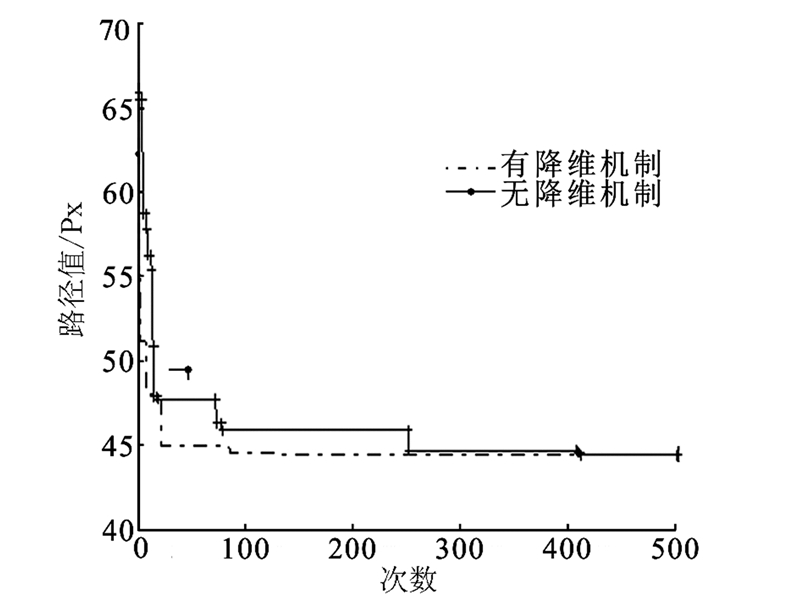 |
| 图 5 降维机制对算法迭代影响的趋势图Fig. 5 Influence of the dimensionality reduction mechanism on algorithm iteration |
 |
| 图 6 降维机制对算法结果影响的统计Fig. 6 Statistics of the influence of dimensionality reduction mechanism on results of algorithm |
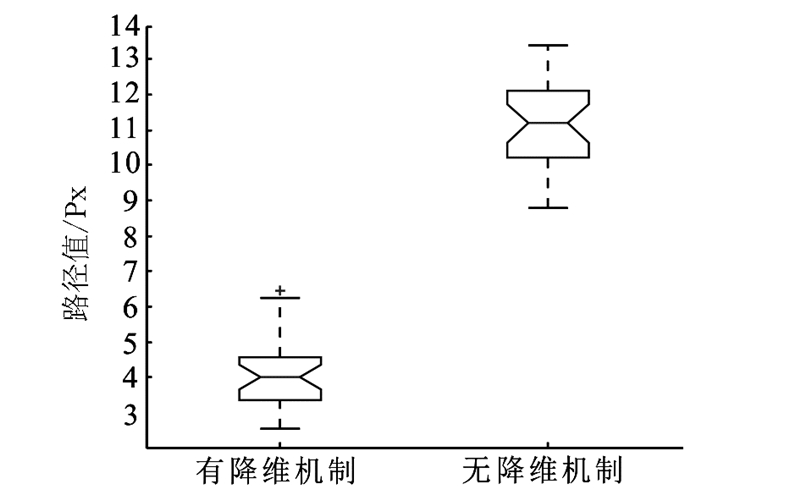 |
| 图 7 降维机制对算法时效影响的统计Fig. 7 Statistics of the influence of dimensionality reduction mechanism on algorithm effectiveness |
根据仿真统计结果及下降趋势图显示,降维机制对算法寻找最小路径效果上有作用。由图5可以看出降维机制加快了算法的收敛速度。由图6可以得到,降维机制呈现了较好的稳定性,30次结果的标准差为0.941 9,而无降维机制为1.297 4;也呈现了较好的搜索能力,30次结果的误差率为2.59%,而无降维机制为3.35%。在规划时间消耗上图7显而易见的表明了其降维机制的优势。
为了能更好的评价4个算法的性能,现将算法参数设置如下:
BBO:岛屿数M=30,最大变异率mmax=0.3,采用上面提到的降维机制和精英策略,以及双向搜索机制;
PSO:粒子个数M=30,惯性常数ωmax=0.8,ωmmin=0.4,c1=0.5,c2=0.5,采用线性动态ω调整策略、降维机制和双向搜索机制;
AFSA:人工鱼个数M=30,拥挤度因子设为2,感知距离为0.1,最大移动步长0.08,最大试探次数10,同样采用双向搜索机制和降维机制;
ABC:人工蜂个数M=30,最大尝试次数Limit=15,同样采用双向搜索机制和降维机制。
每个算法统一迭代次数为2 000次。
为移动机器人在图8环境下进行路径规划,路径起始点为栅格图的左上角(0,0)点,目的地为栅格图的右下角(N-1,N-1)。
 |
| 图 8 仿真环境模型Fig. 8 Simulation environment models |
算法运行在不同的环境模型下的复杂度及理论最小路径统计如表1所示。
| 栅格地图 | 有效顶点数 | 理论最小值 |
| 20×20 | 141 | 28.812 2 |
| 30×30 | 321 | 43.903 0 |
| 40×40 | 575 | 58.993 8 |
| 50×50 | 903 | 73.952 6 |
| 60×60 | 1 305 | 88.820 5 |
| 70×70 | 1 781 | 103.688 4 |
每个算法在每种栅格环境下重复运行30次得到的规划结果和时间消耗结果统计如下表2所示。
| 栅格规模 | 算法 | 最小值 | 最大值 | 均值 | 中间值 | 标准差 | 误差率/% |
| 20×20 (141) | BBO | 29.348 7 | 29.376 2 | 29.349 8 | 29.348 7 | 0.005 1 | 1.87 |
| PSO | 29.348 7 | 35.621 8 | 30.791 4 | 30.398 8 | 1.530 0 | 6.87 | |
| AFSA | 29.348 7 | 29.348 7 | 29.348 7 | 29.348 7 | 0 | 1.86 | |
| ABC | 29.348 7 | 29.404 5 | 29.350 6 | 29.348 7 | 0.010 2 | 1.87 | |
| 30×30 (321) | BBO | 44.216 6 | 45.559 6 | 44.558 5 | 44.555 2 | 0.293 9 | 2.58 |
| PSO | 47.058 9 | 58.530 9 | 51.798 3 | 51.495 1 | 3.418 8 | 17.98 | |
| AFSA | 44.388 2 | 48.034 4 | 46.136 0 | 45.876 3 | 1.056 4 | 5.09 | |
| ABC | 44.582 8 | 52.077 6 | 49.115 8 | 49.384 1 | 2.058 7 | 11.87 | |
| 40×40 (575) | BBO | 59.423 2 | 65.792 1 | 63.229 2 | 63.600 3 | 1.275 3 | 7.18 |
| PSO | 70.058 2 | 92.295 3 | 77.519 8 | 77.268 4 | 4.736 3 | 31.40 | |
| AFSA | 62.941 4 | 73.515 4 | 68.606 0 | 68.770 4 | 2.433 6 | 16.29 | |
| ABC | 64.973 6 | 81.521 4 | 74.413 9 | 74.051 8 | 3.785 0 | 26.14 | |
| 50×50 (903) | BBO | 81.799 4 | 92.407 6 | 88.612 9 | 88.733 3 | 3.271 3 | 19.84 |
| PSO | 90.701 7 | 126.772 0 | 109.324 3 | 108.261 0 | 11.269 8 | 47.85 | |
| AFSA | 87.008 4 | 100.621 0 | 95.752 1 | 96.859 1 | 3.931 5 | 29.50 | |
| ABC | 92.565 6 | 116.311 0 | 105.551 4 | 106.293 5 | 7.353 5 | 42.75 | |
| 60×60 (1305) | BBO | 103.741 0 | 120.983 0 | 114.791 5 | 116.312 5 | 5.918 0 | 29.24 |
| PSO | 121.012 0 | 156.372 0 | 136.067 2 | 136.008 0 | 10.605 7 | 53.19 | |
| AFSA | 117.059 0 | 136.808 0 | 128.630 1 | 131.973 0 | 6.455 5 | 44.82 | |
| ABC | 125.807 0 | 154.789 0 | 142.289 9 | 143.070 5 | 10.756 9 | 60.20 | |
| 70×70 (1781) | BBO | 147.224 0 | 174.286 0 | 158.493 0 | 157.741 0 | 8.401 9 | 52.86 |
| PSO | 141.577 0 | 219.568 0 | 181.430 5 | 177.859 5 | 25.627 5 | 74.98 | |
| AFSA | 132.976 0 | 170.408 0 | 149.900 2 | 148.404 5 | 12.995 1 | 54.21 | |
| ABC | 164.998 0 | 234.324 0 | 194.063 4 | 191.770 0 | 24.829 0 | 87.16 |
由表2中可见,BBO算法除第1种环境与其他算法结果相同以外,其余5种环境下规划效果均好于其他4种算法。表明本文针对机器人路径规划问题,所提出的生物地理优化算法改进策略对于机器人路径规划问题是有效的。
5 结束语本文基于BBO的机器人路径规划问题,提出了复杂环境下基于有效顶点降维策略的移动机器人路径规划算法,并提出惯性迁移操作算子。改进的BBO与人工蜂群算法、人工鱼群算法、粒子群算法进行对比,仿真结果表明所提出的生物地理机器人路径优化算法对于机器人路径规划是有效的。在此基础上,继续研究该算法在多目标路径规划、城市交通实际环境下的汽车路径规划等问题。
| [1] | 朱大奇, 颜明重. 移动机器人路径规划技术综述[J]. 控制与决策, 2010, 25(7):961-967. ZHU Daqi, YAN Mingzhong. Survey on technology of mobile robot path planning[J]. Control and Decision, 2010, 25(7):961-967. |
| [2] | VASUDEVAN C, GANESAN K. Case-based path planning for autonomous underwater vehicles[C]//Proceedings of the 1994 IEEE International Symposium on Intelligent Control. Columbus, USA, 1994:160-165. |
| [3] | LIU Yu, ZHU Shiqiang, JIN Bo, et al. Sensory navigation of autonomous cleaning robots[C]//The 5th World Conference on Intelligent Control Automation. Hangzhou, China, 2004:4793-4796. |
| [4] | RAM A, SANTAMARÍA J C. Continuous case-based reasoning[J]. Artificial Intelligence, 1997, 90(1/2):25-77. |
| [5] | ARLEO A, SMERALDI F, GERSTNER W. Cognitive navigation based on nonuniform Gabor space sampling, unsupervised growing Networks, and reinforcement learning[J]. IEEE Transactions on Neural Network, 2004, 15(3):639-652. |
| [6] | FUJIMURA K, SAMET H. A hierarchical strategy for path planning among moving obstacles[mobile robot][J]. IEEE Transactions on Robotic Automation, 1989, 5(1):61-69. |
| [7] | KO N Y, LEE B H. Avoidability measure in moving obstacle avoidance problem and its use for robot motion planning[C]//IEEE International Conference on Intelligent Robots and System. Osaka, 1996:1296-1303. |
| [8] | GE S S, CUI Y J. New potential functions for mobile robot path planning[J]. IEEE Transactions on Robotics and Automation, 2000, 16(5):615-620. |
| [9] | 陈清阳, 张小波, 孙振平, 等. 非结构化环境下自主车辆轨迹规划方法[J]. 中南大学学报:然科学版. 2011, 42(11):3377-3383. CHEN Qingyang, ZHANG Xiaobo, SUN Zhenping, et al. Trajectory planning for autonomous driving in unstructured environments[J]. Journal of Central South University:atural and Technology, 2011, 42(11):3377-3383. |
| [10] | 王鸿鹏, 杨云, 刘景泰. 高速移动机器人的研究现状与发展趋势[J]. 自动化与仪表, 2011, 26(12):1-4. WANG Hongpeng, YANG Yun, LIU Jingtai. Research and development trend of high-speed mobile robot[J]. Automation and Instrumentation, 2011, 26(12):1-4. |
| [11] | 谭民, 王硕. 机器人技术研究进展[J]. 自动化学报, 2013, 39(7):963-972. TAN Min, WANG Shuo. Research progress on robotics[J]. Acta Automatica Sinica, 2013, 39(7):963-972. |
| [12] | JARADAT M A K, GARIBEH M H, FEILAT E A. Dynamic motion planning for autonomous mobile robot using fuzzy potential field[C]//Proceeding of the 6th International Symposium on Mechatronics and its Applications. Sharjah, UAE, 2009:24-26. |
| [13] | LINGELBACH F. Path planning using probabilistic cell decomposition[C]//IEEE International Conference on Robotics and Automation. New Orleans, USA, 2004:467-472. |
| [14] | MO Hongwei, MENG Longlong. Robot path planning based on differential evolution in static environment[J]. International Journal of Digital Content Technology and its Applications, 2012, 6(20):122-129. |
| [15] | MO Hongwei, XU Lifang. Biogeography migration algorithm for traveling salesman problem[J]. International Journal of Intelligent Computing and Cybernetics, 2011, 4(3):311-330. |



