2. 北华大学 电气信息工程学院, 吉林 吉林 132021;
3. 吉林省水利科学研究院, 吉林 长春 130022;
4. 吉林省计算中心 吉林省计算机技术研究所, 吉林 长春 130012
2. College of Electrical and Information Engineering, Beihua University, Jilin 132021, China;
3. Jilin Water Resources Research Institute, Changchun 130022, China;
4. Computing Center of Jilin Province, Computer Technology Research Institute of Jilin Province, Changchun 130012, China
水是工业的血液、农业的命脉,随着世界人口的不断增长和经济的飞速发展,人类对水资源的需求量不断增加,工业废水和生活废水的排量与日俱增,对受纳水体的环境质量造成严重威胁,治理压力越来越大。2006年我国检测的7大水系的197条河流的408个断面中,Ⅰ类至Ⅲ类水质断面占46%,Ⅳ、Ⅴ类占28%,超Ⅴ类占26%,地表水资源污染十分严重。
水质评估是以水域水质监测指标为基础,按照一定的评估标准对水环境水质进行评估,能够准确反映水域水质状况和水体污染情况,达到提前预测预警的目的。传统的水质评估方法主要有单因子评价法[1]、加权均值指数法[2]和内梅罗污染指数分析法[3]等。由于这些方法在水质评估中存在很多缺陷,往往导致评估结果与实际水质状况差距较大,因此很难满足水质评估的实际要求。如单因子指数法只能反映各个水质参数的污染程度,不能反映水资源整体污染状况,评估精度极低。加权均值指数法克服了参数多少不同的影响,但权值的确定存在不合理和主观性。内梅罗指数法只考虑单因子污染指数的平均值和最高值,过分强调最大浓度污染因子对水资源的影响,忽视了某些浓度小而危害大的污染因子,对水资源水质评价灵敏性不够高,难以区分水资源污染程度的差别。因而,人们在评价水资源污染状况时,试图寻找可以考虑多种水质指标且客观反映水质污染状况的方法。于是基于启发式的各种智能方法被广泛应用于水质评估领域,如基于主成分分析的方法[4, 5]、基于信息熵的方法[6]、基于聚类的方法[7]和人工神经网络方法[8, 9, 10, 11]等。这些方法多是基于统计学理论,要求被研究的样本规模充分大,而在实际问题中往往无法满足,导致了水质评估性能不能令人满意。支持向量机(support vector machine,SVM )方法与传统智能方法相比,不是仅仅以经验风险最小化为目标,而是以结构风险最小化为目标,仅以经验风险最小为约束条件,因此SVM方法特别适合于小样本分类,并具有全局寻优和泛化能力强等优点[12]。目前已有一些学者采用SVM方法进行水质污染预测与评价[13, 14],并且取得了很好效果。但由于传统SVM算法的参数选取多是依赖经验或人工反复尝试,通常很难选择到最佳的参数组合,存在分类效果因人而异、参数选择时间长等缺点,这在一定程度上限制了其应用和发展。
本文SVM的参数选择过程中引入遗传算法(genetic algorithms,GA),利用其较强的全局搜索能力进行参数优化,建立了一种进化SVM模型,并将所提出的模型应用于水质评估。为验证方法的有效性,将该模型分别应用于松花江松原段、松花江哈尔滨段、黄河甘肃段和吉林桦甸关门砬子水库的真实数据上进行测试。实验结果表明,建立的进化SVM水质评估模型在分类精度和泛化能力上较经典SVM方法和BP神经网络方法都有所提高。
1 进化SVM方法 1.1 SVM方法SVM方法是20世纪90年代由Vapnik提出的,是建立在统计学习理论基础上的一种新方法[12]。其优化目标为结构风险最小化,能依靠有限样本信息实现模型复杂性和学习能力之间最佳折中。由于SVM方法适用于小样本分类问题,并具有全局最优性能和较好的泛化能力,因而在模式分类[15]和预测分析[16]等方面得到了广泛应用。
SVM的基本理论是从二分类的问题提出的。设样本集{ xi,yi},x∈ Rd,i=1,2,…,n,其中n为样本个数;d为样本向量xi的维数;yi∈{-1,1},代表分类类别。如果数据为线性可分的,则存在超平面将2组数据分开,如图1所示。
 |
| 图 1 最优超平面示意图Fig. 1 Sketch diagram of optimal hyperplane |
设超平面为
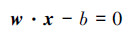
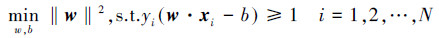
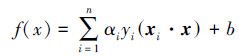
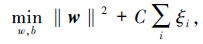
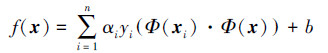
为避免低维空间到高维空间映射的复杂运算,用低维空间的核函数代替高维空间中的内积运算,即若有K(x,y)=Φ(x)·Φ(y),得到的超平面为

在SVM中,核函数的选取对算法的效果有重要影响,常用的核函数类型主要有线性核函数、多项式核函数、径向基核函数和Sigmoid核函数等,其中最为常用的是径向基核函数,其形式为
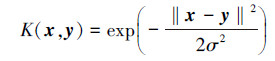
惩罚系数C和核函数中的参数,如径向基中的宽度σ的选取是SVM算法中较为关键的问题。但是如何选取最佳的SVM参数一直没有一个统一的方法,这在很大程度上限制了它的实际应用。本文采用GA方法进行SVM的参数选取,即惩罚系数C和径向基函数宽度σ 的选取。主要过程如下:
1)编码。在对SVM 2个参数的组合进行优化时,RBF核函数参数σ和惩罚因子C取值范围采用二进制编码,编码分别为m1位和m2位的二进制串,将m1+m2位二进制编码组合就得到个体染色体基因串,个体染色体基因串结构如图2所示。
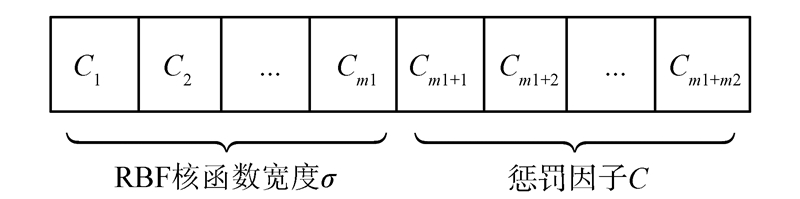 |
| 图 2 染色体结构Fig. 2 Structure of chromosome |
2)适应度评价函数。本文采用5折交叉验证法进行训练,即将训练样本分成5份,每次随机选择4份进行训练,另外1份用作验证集。GA的适应度通过验证集的误差进行定义,即

3)选择操作。本文采用基于排序的选择方案,按照适应度值对种群内的全部P个个体进行排序,第i个个体被选择的概率为
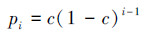
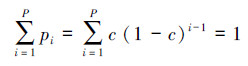
4)交叉和变异操作。在选择操作中用于繁殖下一代的个体中,对2个不同染色体相同位置上的基因以交叉概率pc进行交换,从而产生新的染色体。变异算子以一定的变异概率pm随机改变字符串某个位置上的值,随机将二进制编码基因串某个位置0变为1,或将1变为0。交叉概率pc和变异概率pm按照文献[17]的算法进行选择,使pc和pm能够随适应度自动改变。
算法的流程如图3所示。
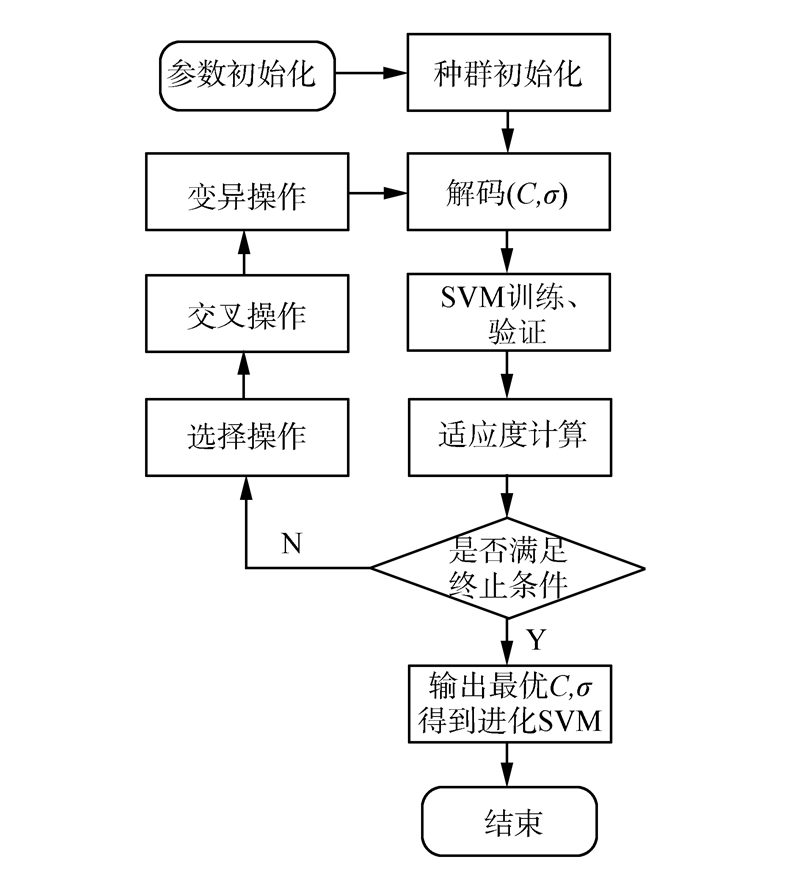 |
| 图 3 进化SVM流程Fig. 3 Flowchart of evolutionary SVM |
本文的实验数据来自松花江松原段、松花江哈尔滨段、黄河甘肃段和吉林桦甸关门砬子水库日常水质监测数据,主要水质监测项目有pH、溶解氧(dissolved oxygen,DO)、高锰酸盐指数(permanganate index,PI)、化学需氧量(chemical oxygen demand,COD)、生化需氧量(biochemical oxygen demand,BOD)、氨氮、总磷(total phosphorus,TP)、总氮(total phosphorus,TN)、挥发酚(volatile phenol,VP)、石油类和大肠种群等。剔出由于各种原因造成的缺失数据,其样本数、监测位置和监测项目详细信息如表1所示。其中松花江松原段选择2002年至2006年连续5年的每年丰水期、平水期和枯水期3个时段的水质监测数据;松花江哈尔滨段选择2012年2月至10月连续9个月的4个断面、2个监测点,每月1次的水质监测数据;黄河甘肃段选择2010年全年18个监测断面,每月1次的水质监测数据;吉林桦甸关门砬子水库选择2014年7月到2015年8月每天6次水质监测数据。水质评价执行地面水环境质量标准GB3838-2002,水质级别执行5级标准[18]。
| 数据来源 | 样本数 | 监测位置 | 监测项目 |
| 松花江松原段 | 45 | 松原牧场、西大嘴子、泔水缸 | COD、BOD、氨氮、VP、石油类 |
| 松花江 哈尔滨段 | 57 | 三家子、二水源、水泥厂、大亮子、金河湾湿地、呼兰河口 | pH、DO、PI、COD、BOD、氨氮、TP、TN、粪大肠菌群 |
| 黄河 甘肃段 | 161 | 扶河桥、包兰桥、什川桥、靖远桥、五佛寺、德高桥、地沟桥、折桥、曳湖峡、玉井、洮园桥、涅水桥、桦林、伯阳桥、葡萄园、平镇桥、拦洪坝、宁县桥头 | COD、氨氮、TP、VP、粪大肠菌群 |
| 桦甸关门砬子水库 | 2 142 | 桦甸关门砬子水库 | DO、PI、氨氮、TP、TN |
本文选取每组数据源中2/3的数据作为训练样本,1/3的数据作为测试样本,训练过程采用5折交叉验证。水质监测指标作为输入向量,水质级别作为输出向量,核函数选用常用的RBF函数。采用1.2节提出的方法对SVM的参数进行寻优,4个数据集的进化代数与适应度关系曲线分别如图4~7所示,当惩罚因子C、RBF核函数参数σ和交叉确认准确率分别取表2中的数值时,SVM分类精度和泛化能力最佳。
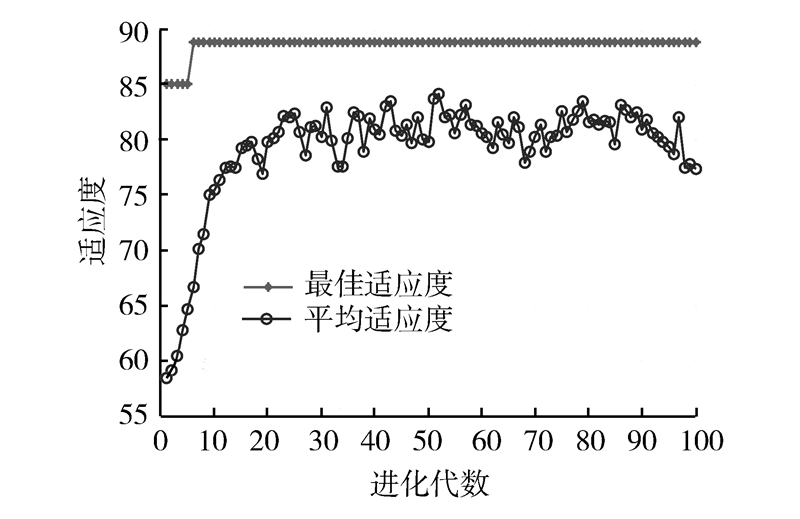 |
| 图 4 松花江松原段GA适应度曲线Fig. 4 GA fitness curves on Songyuan section, Songhua River |
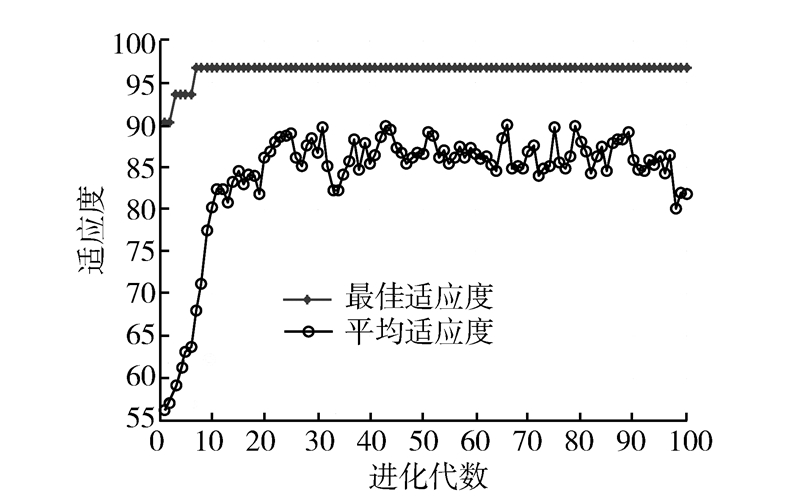 |
| 图 5 松花江黑龙江段GA适应度曲线Fig. 5 GA fitness curves on Heilongjiang section,Songhua River |
 |
| 图 6 黄河甘肃段GA适应度曲线Fig. 6 GA fitness curves on Gansu section,Yellow River |
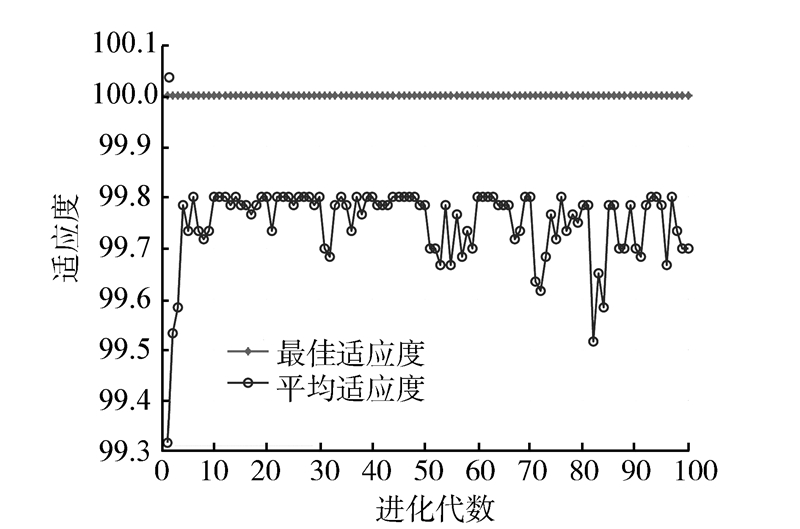 |
| 图 7 桦甸关门砬子水库GA适应度曲线Fig. 7 GA fitness curves on HuaDian Guanmenlazi dam |
| 数据来源 | C | σ | 交叉确认准确率/% |
| 松花江松原段 | 2.549 3 | 3.304 9 | 88.888 9 |
| 松花江哈尔滨段 | 1.400 1 | 3.215 3 | 96.774 2 |
| 黄河甘肃段 | 2.285 1 | 289.598 2 | 93.814 4 |
| 桦甸关门砬子水库 | 0.162 975 | 58.629 9 | 100 |
为验证本文方法的有效性,将其结果与经典SVM的结果进行了比较。经典SVM选择目前被广泛使用的台湾大学林智仁教授开发的免费软件包LIBSVM[19]进行计算。算法中的主要参数均采用默认值,即惩罚因子C=1,RBF核函数参数σ取样本数据属性数的倒数。进化SVM算法中的惩罚因子C和RBF核函数参数σ按表2取值。水质评估结果如表3所示。由表3可以看出,进化SVM水质评价模型的识别精度较经典SVM水质评价模型分别提高16.7%、12.5%、 33.3%和6.7%,较BP神经网络方法分别提高7.7%、0%、1.7%和40.9%,这说明本文方法具有良好的分类精度和泛化性能。
| % | ||||
| 方法 | 松花江松原段 | 松花江哈尔滨段 | 黄河甘肃段 | 桦甸关门砬子水库 |
| BP | 72.22 | 85.71 | 92.19 | 67.04 |
| 经典SVM | 66.67 | 76.19 | 70.31 | 88.52 |
| 进化SVM | 77.78 | 85.71 | 93.75 | 94.44 |
本文建立的进化SVM模型采用的对SVM的惩罚因子C和RBF核函数参数σ进行参数优化,对比经典SVM方法具有一定的优势。将其应用于水质评估问题中,实验结果表明该方法可获得较传统算法更好的精度。本文为水质综合评估提供了一条新途径,对及时掌握流域水污染状况和水文特征具有重要意义。
| [1] | 朱灵峰, 王燕, 王阳阳, 等. 基于单因子指数法的海浪河水质评价[J]. 江苏农业科学, 2012, 40(3):326-327. ZHU Lingfeng, WANG Yan, WANG Yangyang, et al. Water quality assessment of Hailang River using single factor index method[J]. Journal of Jiangsu Agricultural Sciences, 2012, 40(3):326-327. |
| [2] | 张龙江. 水质评价的模糊综合评判——加权平均复合模型应用[J]. 环境工程, 2001, 19(6):53-55. ZHANG Longjiang. Application of fuzzy comprehensive judgement and weighted average models to water quality assessment[J]. Environmental Engineering, 2001, 19(6):53-55. |
| [3] | 钱天鸣, 余波. 内梅罗污染指数在运河水质评价中的应用[J]. 环境污染与防治, 1999, 21(增刊):67-68, 71. QIAN Tianming, YU Bo. Application of the canal water quality evaluation using Nemerow pollution index[J]. Environmental Pollution & Control, 1999, 21(S):67-68, 71. |
| [4] | 张召跃, 王海燕, 朱灵峰, 等. 主成分分析法在水节霉生长水体水质评价中的应用[J]. 环境工程学报, 2011, 5(5):1035-1040. ZHANG Zhaoyue, WANG Haiyan, ZHU Lingfeng, et al. Application of principal component analysis in quality evaluation of water body with Leptomitus lacreus growth[J]. Chinese Journal of Environmental Engineering, 2011, 5(5):1035-1040. |
| [5] | 李凤超, 刘存歧, 管越强, 等. 应用多元分析方法评价白洋淀水质现状[J]. 河北大学学报:自然科学版, 2006, 26(4):405-410. LI Fengchao, LIU Cunqi, GUAN Yueqiang, et al. Evaluating current water quality of Baiyangdian Lake by using multi-variate analysis[J]. Journal of Hebei University:Natural Science Edition, 2006, 26(4):405-410. |
| [6] | LIU L, ZHOU J Z, AN X L, et al. Using fuzzy theory and information entropy for water quality assessment in Three Gorges region, China[J]. Expert Systems with Applications, 2010, 37(3):2517-2521. |
| [7] | 张萌, 倪乐意, 谢平, 等. 基于聚类和多重评价法的河流质量评价研究[J]. 环境科学与技术, 2009, 32(12):178-185. ZHANG Meng, NI Leyi, XIE Ping, et al. Water quality assessment of a large river based on multiple assessment method and cluster analysis[J]. Environmental Science & Technology, 2009, 32(12):178-185. |
| [8] | WEN C G, LEE C S. A neural network approach to multiobjective optimization for water quality management in a river basin[J]. Water Resources Research, 1998, 34(3):427-436. |
| [9] | 黄胜伟, 董曼玲. 自适应变步长BP神经网络在水质评价中的应用[J]. 水利学报, 2002, (10):119-123. HUANG Shengwei, DONG Manling. Application of adaptive variable step size BP network to evaluate water quality[J]. Journal of Hydraulic Engineering, 2002, (10):119-123. |
| [10] | 罗定贵, 王学军, 郭青. 基于MATLAB实现的ANN方法在地下水质评价中的应用[J]. 北京大学学报:自然科学版, 2004, 40(2):296-302. LUO Dinggui, WANG Xuejun, GUO Qing. The application of ANN realized by MATLAB to underground water quality assessment[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2004, 40(2):296-302. |
| [11] | 曹艳龙, 汪西莉, 周兆永. 基于BP神经网络的渭河水质评价方法[J]. 计算机工程与设计, 2008, 29(22):5910-5912, 5916. CAO Yanlong, WANG Xili, ZHOU Zhaoyong. Water quality assessment method of Wei river based on BP neural network[J]. Computer Engineering and Design, 2008, 29(22):5910-5912, 5916. |
| [12] | VAPNIK V. The nature of statistical learning theory[M]. New York:Springer Verlag, 1995:267-290. |
| [13] | XIANG Y R, JIANG L Z. Water quality prediction using LS-SVM with particle swarm optimization[C]//Second International Workshop Discovery and Data Mining. Moscow, Russia, 2009:901-904. |
| [14] | SINGH K P, BASANT N, GUPTA S. Support vector machines in water quality management[J]. Analytica Chimica Acta, 2011, 703(2):152-162. |
| [15] | 张艳秋, 王蔚. 利用遗传算法优化的支持向量机垃圾邮件分类[J]. 计算机应用, 2009, 29(10):2755-2757. ZHANG Yanqiu, WANG Wei. E-mail classification by SVM optimized with genetic algorithm[J]. Journal of Computer Applications, 2009, 29(10):2755-2757. |
| [16] | SAINI L M, AGGARWAL S K, KUMAR A. Parameter optimisation using genetic algorithm for support vector machine-based price-forecasting model in National electricity market[J]. IET Generation, Transmission & Distribution, 2010, 4(1):36-49. |
| [17] | SRINIVAS M, PATNAIK L M. Adaptive probabilities of crossover and mutation in genetic algorithm[J]. IEEE Transactions on Systems Man and Cybernetics, 1994, 24(4):656-667. |
| [18] | 中国环境科学研究院. GB3838_2002地表水环境质量标准[S]. 北京:中国环境科学出版社, 2002. China Environmental Science Research Institute. GB3838_2002 The surface water environment quality standard[S]. Beijing:China Environmental Science Press, 2002. |
| [19] | CHANG C C, LIN C J. LIBSVM:a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3):27. |



