机械臂的大范围柔顺控制是指使机械臂能够在任何构型下实现大范围的力柔顺运动的过程。运行于地球同步轨道上的空间机械臂由于工作在微重力环境下,大范围的柔顺控制实施起来不会受到重力等附加力的干扰,可非常容易地实现; 但重力环境下的大范围柔顺控制问题一直未得到很好地解决,其中最重要的原因是不能很好地进行实时重力补偿。目前机械臂重力补偿普遍采用的是借助外部机械装置的被动补偿法,如文献[1]提出了一种基于气浮和静力平衡的混合重力补偿装置,文献[2]利用弹簧机构设计了一种名为Freebal的重力补偿设备,这些被动补偿设备不仅经济代价昂贵,而且会对机械臂的运动产生影响和限制[3]。也有部分学者尝试通过算法对机械臂各关节和末端重力进行主动补偿。文献[4]提出一种基于最大允许有效载荷的特殊运算来减少重力的影响; 文献[5]采用基于能量的概念进行重力补偿; 文献[6]采用基于李雅普诺夫控制理论的方法进行重力补偿,但以上3种方法计算量较大,不适合用作实时补偿算法。文献[7]提出了一种基于机械臂运动学的方法进行重力补偿和实现基于力的阻抗控制的方法,取得了较好的实时控制效果。另外,在基于末端受力/力矩(F/T)传感器的柔顺控制方案中,对柔顺控制过程的直接影响来自于末端质量,而与各关节和连杆的质量关系不大,因此以上各算法都不能完全适用; 同时,由于末端运动速度快、运动范围大,采用机械装置进行重力补偿的难度和成本都比较大。针对这种情况,目前普遍的方法是在进行柔顺控制之前,先将末端F/T传感器置零,排除重力对F/T传感器测量值的影响,但这种做法有一个严重的缺点,就是在柔顺控制的过程中末端不能进行俯仰或翻滚姿态的变化,否则重力的影响依然存在,这较大程度地限制了柔顺控制的范围和实际效果。
本文提出的基于末端F/T传感器的重力环境下大范围柔顺控制方法,采用基于机械臂运动学的方法对机械臂末端的重力进行实时补偿,采用关节空间基于位置的阻抗控制策略进行柔顺控制,能够使机械臂在运动的任何时刻、任何末端位姿下都具备柔顺能力,使其更加贴近生物臂的操作过程,而整个过程不需要额外添加任何设备。
1 6-DOF机械臂系统本文以自主研发的6自由度小型空间机械臂为平台,阐述重力环境下的大范围柔顺控制方法,该机械臂系统的结构如图 1所示,为方便以下简称为6-DOF机械臂系统。该系统由6个关节、2个连杆及1个末端执行器组成,在末端执行器与关节6之间装有F/T传感器,也称六维力传感器,用于感知末端F/T情况。机械臂总长约1.2 m,重约40kg,具备6个自由度,末端工具可根据需要更换,该系统可应用于空间货物自动抬升机构、机器人航天员、空间站舱内外小型服务系统、舱外维护与操作设备等领域。
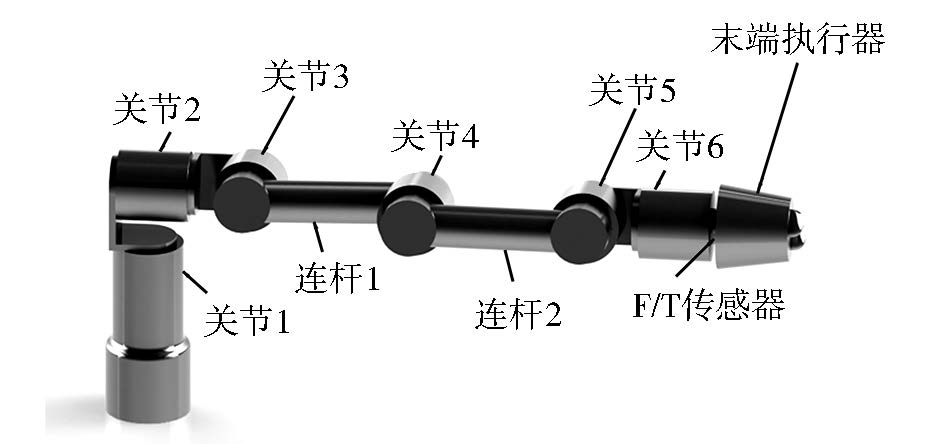 |
| 图 1 6-DOF机械臂系统Fig. 1 6-DOF manipulator system |
图 2为该机械臂系统的坐标系定义图,其中坐标系{0}为基坐标系,坐标系{1}~{6}分别为6个关节的坐标系定义,坐标系{7}为机械臂末端操作工具的坐标系定义,坐标系{8}为末端F/T传感器的坐标系定义。
 |
| 图 2 6-DOF机械臂坐标系 Fig. 2 Coordinate system of the 6-DOF manipulator |
根据坐标系定义图可得该机械臂的D-H参数如表 1所示。
| 连杆 | αi-1/(°) | ai-1/mm | θi/(°) | di/mm |
| 1 | 0 | 0 | 0 | 372.6 |
| 2 | -90 | 0 | 90 | 205.2 |
| 3 | -90 | 0 | -90 | 0 |
| 4 | 0 | 514.0 | 0 | -236.6 |
| 5 | 0 | 512.0 | -90 | 0 |
| 6 | -90 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 545.6 |
由于该类机械臂的末端运动范围较大,且都是采用远程遥操作的模式实施控制,要求机械臂在运动过程的任何时刻和构型下能够对外力进行柔顺,以防止发生意外,损坏机械臂系统自身或者其他装备。具备重力环境下大范围柔顺控制能力可以有效消除末端重力对力传感器测量值的影响,实现地面大范围柔顺运动,有助于地面调试阶段做好全面的实验和分析,保证空间机械臂系统进入太空后能够良好地运行。
2 大范围柔顺控制方法 2.1 柔顺控制策略选择实现主动柔顺控制的策略有多种,目前比较普遍的有阻抗控制、力/位混合控制、自适应控制及智能控制等[8]。其中,力/位混合控制[9]的原理是通过机械臂的雅克比矩阵将作业空间任意方向的力和位置分配到各个关节控制器上,计算量比较大,且需要准确知道力/位控制的方向及期望力/位矢量,理论明确,付诸实施难; 自适应控制[10]由于理论比较复杂,需要同时控制的参数较多,应用于实际控制的例子并不多; 智能控制策略为新兴的机器人控制方法,多采用神经网络控制[11]或模糊控制[12]做为核心控制方法,从研究成果来看,目前仍处于起步阶段,方案尚未成熟,有一定的局限性。相比之下,自从Hongan[13]在1984年提出机器人的阻抗控制方法后,许多学者对阻抗控制进行了深入研究,发展出了多种成熟的阻抗控制方法,并成功应用于机器人的柔顺控制现场。本文就是采用基于阻抗控制的策略,来实现重力环境下大范围柔顺控制的。
阻抗控制本身又可分为基于位置的阻抗控制和基于力的阻抗控制2种,由于大部分机器人都是以位置控制器为内部控制机构,因此采用基于位置的阻抗控制策略可以降低柔顺控制的复杂程度,保证柔顺控制的效率。基于位置的阻抗控制又可分为笛卡尔空间基于位置的阻抗控制和关节空间基于位置的阻抗控制。其中笛卡尔空间基于位置的阻抗控制,需要设计专门的笛卡尔空间力控制器,来调节笛卡尔空间期望力与实际力的跟踪精度; 而关节空间基于位置的阻抗控制,则只需要进行一次逆运动学计算,将工作空间的位姿反解到各个关节的位置便可,理论清晰,实施起来也简单,这种方法已经在国际空间站日本机械臂SFA[14]中得到了成功的应用。
基于以上分析,本文将采用关节空间基于位置的阻抗控制策略实现重力环境下的机械臂大范围柔顺控制。
2.2 实时重力补偿算法机械臂各部件的重力都会影响机械臂的运动控制过程[15],本文将重点放到机械臂末端模块重力对柔顺控制过程的影响,这种影响直接来自于末端重力对F/T传感器测量值的影响。如果不进行重力补偿,系统进入柔顺控制模式后,机械臂会跟随重力下掉,使得柔顺控制无法正常实施。因此,大范围柔顺控制技术的关键在于能够在运动过程中实时对末端重力进行补偿,使得补偿后机械臂不受外力作用时,在任何末端位姿下,基坐标系下各方向力和力矩都趋于零。本文将采用基于机械臂运动学的方法,对机械臂末端重力进行实时补偿。
图 3为6自由度机械臂平台下的末端重力补偿原理示意图,可以看出,在不对机械臂末端施加任何外力的情况下,安装在机械臂末端与机械臂关节6之间的F/T传感器的测量值,由于受到末端重力的影响,是不为零的; 而在柔顺控制的过程中,需要对F/T传感器测量到的外作用力进行柔顺运动。因此需要对F/T传感器测量到的数据进行处理,将测量值中的重力产生的力及力矩去除,使得处理后的测量值在任何机械臂构型下都只包含外力部分。
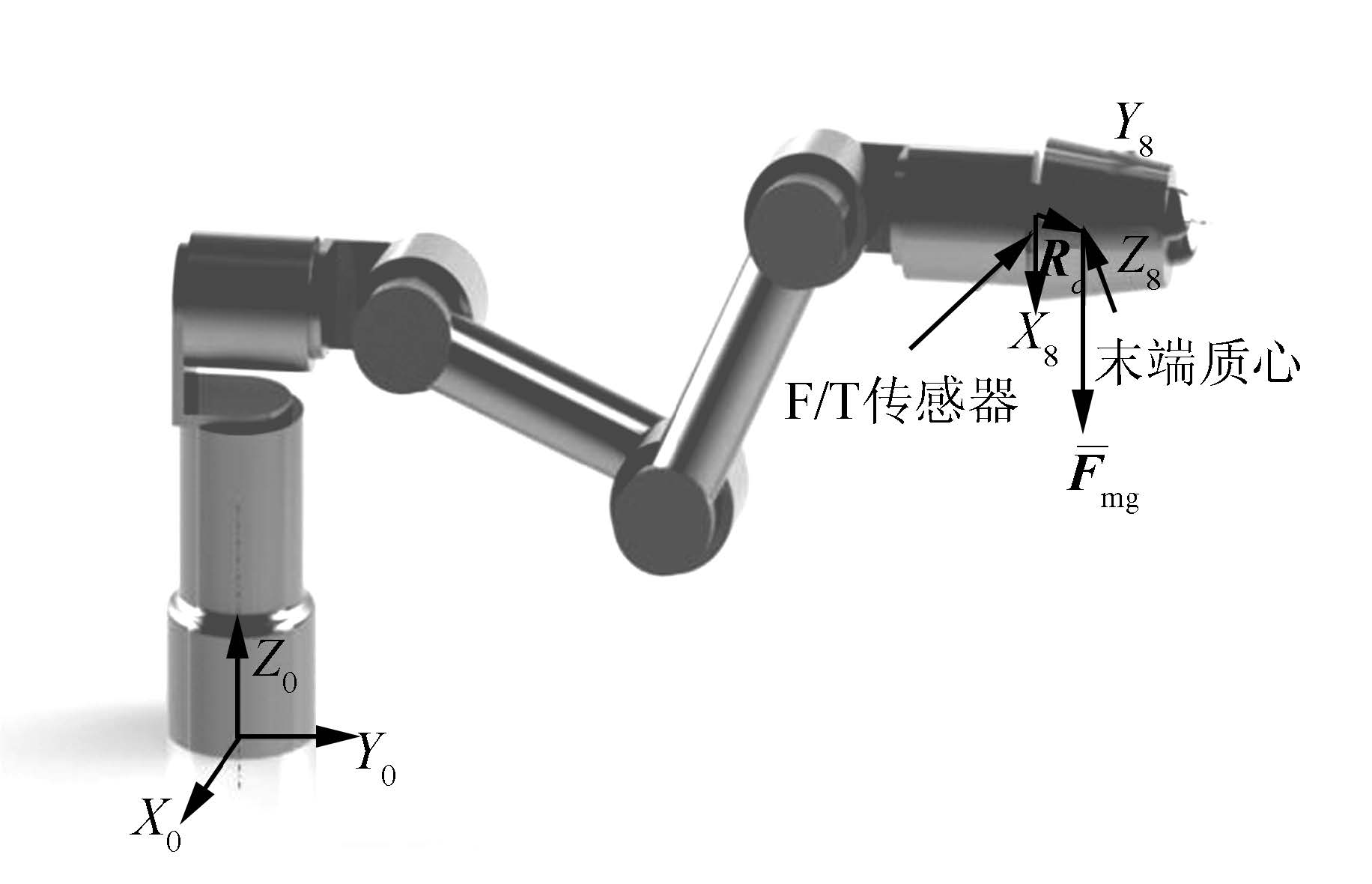 |
| 图 3 重力补偿算法原理示意Fig. 3 Explanation of gravity compensation theory |
首先,要求得F/T传感器坐标系相对于基坐标系的变换关系,由机械臂的D-H参数表及坐标系关系图,可得各坐标系的旋转关系如下:

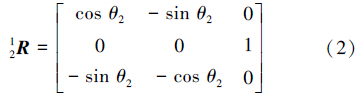
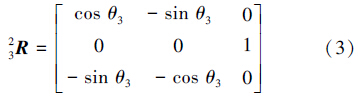




式(1)~(7)中: i-1iR表示坐标系{i}相对于坐标系{i-1}的旋转关系,0iR表示坐标系{i}相对于坐标系{0}的旋转关系,其中坐标系{0}为机械臂基坐标系,坐标系{6}为关节6的坐标系。由于该机械臂的关节6与F/T传感器固定在一起,且坐标系方向相同,故这里为了计算方便,用关节6相对于基坐标系的旋转关系06R表示F/T传感器坐标系相对于基坐标系的旋转关系Tran,且有
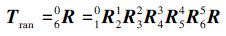
令Fs=Fs Ts,其中Fs表示F/T传感器测量到的3个方向的力矢量,Ts表示F/T传感器测量到的3个方向的力矩矢量,Fs为F/T传感器的测量值。
将测量得到的力和力矩矢量分别变换到基坐标系下:

将末端质心矢量Rc从F/T传感器坐标系变换到基坐标系下:

令Fmg=0,0,-mg,其中m为末端的质量,g为重力加速度。
计算出基坐标系下重力对F/T传感器的作用力矩:
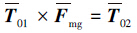
从基坐标系下F/T传感器的测量值中,减去重力和重力矩:

式中: F为机械臂基坐标系{0}下,进行重力补偿后的F/T传感器测量到的力和力矩值。
2.3 大范围柔顺控制方法的实现图 4为本文提出的重力环境下大范围柔顺控制原理方框图,该柔顺控制方法采用关节空间基于位置的阻抗控制策略实现,由图 4可以得出机械臂关节位置控制器输入为
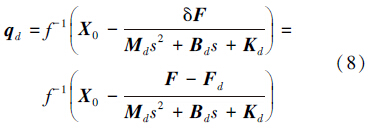
 |
| 图 4 重力环境下大范围柔顺控制原理 Fig. 4 Structure of wide range compliance control in gravity environment |
式中: X0为机械臂末端笛卡尔空间目标位姿,函数f为机械臂关节空间到笛卡尔空间的变换函数,即运动学正解函数; 其逆函数f-1可将笛卡尔空间机械臂末端位姿转换为机械臂各关节的位置,即运动学逆解函数。f-1可采用变量分离法[16]求得,具体求解过程将在后面做出详细阐述。F为经重力补偿后的机械臂基坐标系下F/T传感器的测量值,Fd为机械臂末端与环境的期望接触力。
Mds2+Bds+Kd是系统的期望阻抗特性,Md为机械臂理想惯性参数,对有大加速度的高速运动或会产生冲力的运动影响较大; Bd为机械臂理想阻尼参数,对中速运动或存在较强干扰时影响较大; Kd为机械臂理想刚度参数,对平衡状态附近的低速运动影响较大[17]。Md、Bd、Kd均为N阶对角阵,N代表机械臂的自由度,其对角线的每个元素分别代表X、Y、Z轴平动和转动的期望阻抗特性。
式(8)中: F=ΦFs,其中Φ为重力补偿算法,其求取过程已在2.2节中详细阐述,Fs为F/T传感器实时测量的F/T传感器坐标系下的力和力矩矢量。
以下探讨大范围柔顺控制系统的计算机实现过程。
由
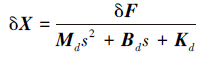
得
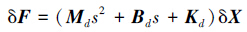
即
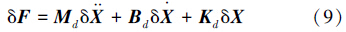
对式(9)采用后向差分离散可得
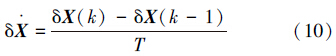
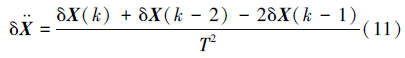
式中: T为系统的采样周期,将式(10)、(11)代入式(9)可得

即
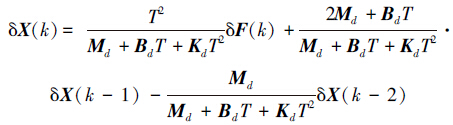
令

则有
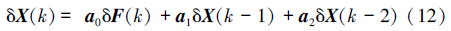
由式(12)可见,当前位姿修正值δX(k)仅与当前F/T偏差值δF(k)及前2个周期的位姿修正值δX(k-1)、δX(k-2)有关,在计算第1个和第2个位置偏差时,可令δX(-1)和δX(-2)为零。由此可通过计算机实现该控制系统。
2.4 6-DOF机械臂系统运动学反解本节主要阐述机械臂笛卡尔空间位姿到关节空间位置的变换过程,即函数f-1的求解过程。
根据齐次变换矩阵的含义,基坐标系到机械臂各关节坐标系的齐次变换矩阵可表示为
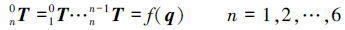
由表 1中机械臂的D-H参数得各连杆变换矩阵如下:

由此可求得机械臂末端的T变换矩阵:

令x、y、z分别表示末端坐标系原点相对于机械臂基坐标系{0}的位置,α、β、θ分别表示末端坐标系相对基坐标系{0}的横滚、俯仰、偏转姿态角,按照3-2-1姿态角顺序,分别为rz、ry、rx,则有

由式(13)与式(14)得
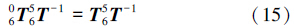
令式(15)等式两边元素(3,1),(3,2),(3,3)分别相等,得
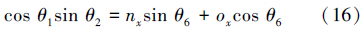
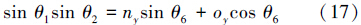
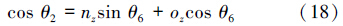
同理可得

令式(19)等式两边元素(2,4)相等,结合式(16)~(18)得

利用三角代换:
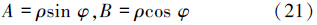
式中:  ,φ=arctan 2(A,B),将式(21)代入式(20)可解得
,φ=arctan 2(A,B),将式(21)代入式(20)可解得
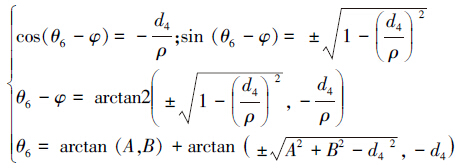
式中

由式(18)得

由式(16)、(17)可得: 当sinθ2≠0时,
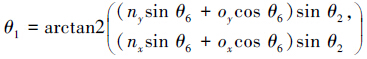
当sin θ2=0时,θ1为任意值。
令式(19)两边元素(1,4)和(3,4)分别相等可得关于

式中
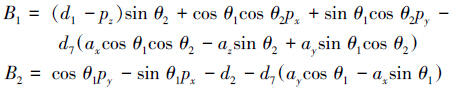
令

解方程组(22)得

令式(19)两边元素(1,2)、(3,2)分别相等得
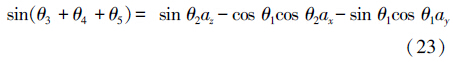

由式(23)、(24)得

至此可分别求出,θ6、θ2、θ1、θ4、θ3、θ5,其中θ6、θ2、θ4各有2组解,反解结果共有8组解,使用时可根据需求,选择最优的一组解。
3 实验验证 3.1 重力补偿算法验证实验方法: 控制机械臂做大范围的运动,使其机械臂末端位姿发生较大变化,但不对末端施加任何外力; 采集整个过程中F/T传感器的测量值,及经实时重力补偿后基坐标系下的各方向力和力矩的计算值。实验结果如图 5所示。
 |
| 图 5 重力补偿算法验证 Fig. 5 Verification of gravity compensation |
从图 5(a)~(b)中可以看出,在实验过程中,F/T传感器力和力矩的测量值都发生了大幅度的变化,尤其是X、Y方向的力及力矩,这说明运动过程使得与F/T传感器固定在一起的机械臂末端姿态发生了大幅变化,且翻滚姿态(对应于X、Y方向力与力矩)变化较大,俯仰姿态(对应于Z方向力与力矩)有小幅变化。由于实验过程中末端未受到自身重力以外力的作用,基坐标系下各方向力和力矩的理论计算值应均为零,而从图中可以看出,实验过程中经重力补偿后基坐标系下各方向力的实际计算值在-4~3 N,各方向力矩的实际计算值在-0.5~0.2 N•m,与理论值存在一定误差,误差的来源包括机械臂运动学建模误差、F/T传感器测量误差、计算过程舍入误差、机械振动等,这里不做为重点分析。
从实验分析结果看,该基于机械臂运动学的重力补偿算法,各方向力补偿的误差约为±4 N,力矩补偿的误差约为±0.5 N•m; 由于机械臂本身都具有一定的柔性,经操作验证,这些误差在实际应用过程中是可以接受的。可见,该重力补偿方法能够适用于机械臂大范围运动下的实时末端重力补偿。
由于重力补偿误差的存在,机械臂的柔顺控制系统在静态时是不稳定的,为了解决这一问题,在具体实施时还要对实时重力平衡后基坐标系下各方向力和力矩进行钝化处理,即当计算得到的基坐标系下某方向的力(或力矩)的绝对值小于FN(或TN)时,不对该方向的力(或力矩)进行柔顺,其中FN≥4 N,TN≥0.5 N•m,且二者的值越小柔顺控制效果越好。
3.2 大范围柔顺控制效果验证实验过程中,机械臂系统阻抗模型参数取值为(仅列举对角元素)

值得注意的是,机械臂阻抗模型参数的选取是十分重要的环节,直接影响最终柔顺控制效果。其选取过程在文献[8]中已做出详细介绍,本文不再赘述。
机械臂期望接触力和力矩为
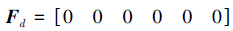
机械臂柔顺控制钝化处理参数为
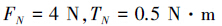
实验方法: 将机械臂末端目标位姿设置为固定值(此时机械臂构型如图 6(a)所示),对末端施加外力,使得机械臂跟随外力做大范围运动,记录下机械臂运动过程中经重力补偿后基坐标系下各方向的F/T,和相应的机械臂位姿修正值。实验过程如图 6所示,实验结果如图 7所示。
 |
| 图 6 6-DOF机械臂柔顺控制实验Fig. 6 Compliance control experiment of 6-DOF manipulator |
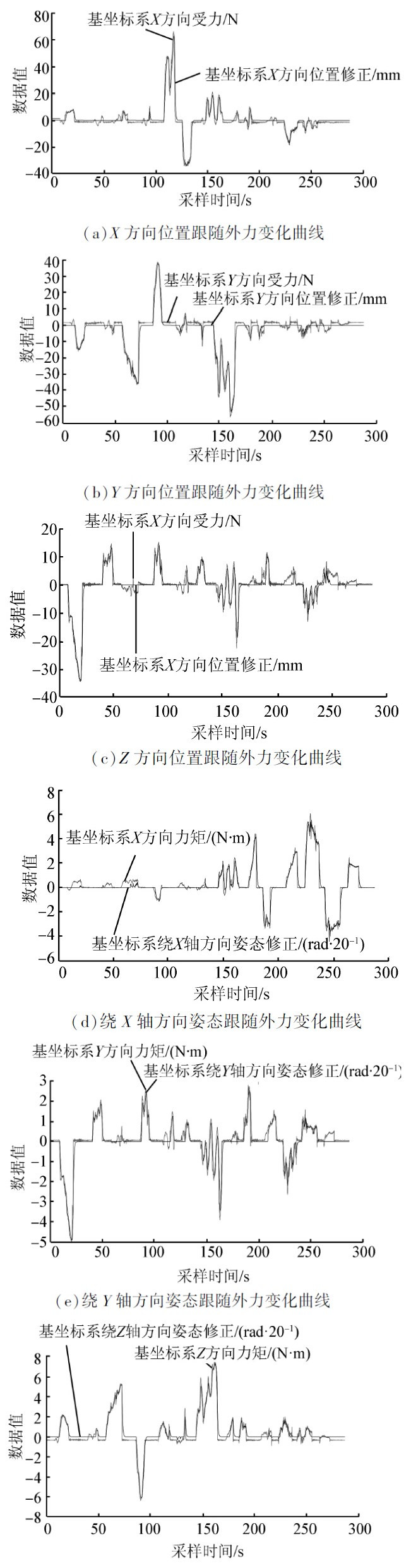 |
| 图 7 机械臂末端位姿修正跟随外力变化曲线Fig. 7 Relationship between the manipulator end revised posture and external force |
图 6中,(a)为机械臂末端目标位姿构型,(b)~(h)为机械臂末端跟随持续外力进行大范围柔顺运动的过程,其中,(b)为沿基坐标系Z轴正方向运动,(c)为沿Z轴负方向运动,(d)为沿X轴正方向运动,(e)为沿X轴负方向运动,(f)为沿Y轴正方向运动,(g)为沿Y轴负方向运动,(h)为绕X轴方向运动。在外力消失后,机械臂能够很快地恢复到(a)构型,成功地实现外力跟随,并能在无外力作用时稳定在目标位姿。
从图 7的实验结果可以看出: 1)机械臂在静态时是稳定的,即经过钝化处理,机械臂在零点附近,不受外力作用时,修正值没有出现波动状态,因此机械臂系统也不会出现抖动现象,总能保持稳定状态; 2)在大范围内任何机械臂构型下柔顺控制系统的位姿修正量能够很好地跟随外力,即在整个大范围运动过程中,任何末端位姿下,外作用力大于4 N,或者外作用力矩大于0.5 N•m时,控制系统能够快速准确地跟随外力调整末端位姿,使机械臂的末端跟随外力运动,实现力柔顺控制。
重力环境下大范围柔顺控制取得了良好的效果,证明了方案的可行性和有效性。
4 结束语为了使机械臂在重力环境下实现大范围的柔顺控制,提出了一种重力环境下机械臂大范围柔顺控制方法。采用基于机械臂运动学的方法,对机械臂末端重力进行实时补偿,消除机械臂末端重量对末端F/T传感器测量值的影响,然后通过关节空间基于位置的阻抗控制策略实现柔顺控制,并详细阐述了各个环节的实现过程。对大范围柔顺控制效果进行了验证,结果表明本文所提方法能够实现机械臂在大范围内任何末端位姿下的外力跟踪,使得机械臂在运动控制的整个过程都具备柔顺能力,且静态时能够保持稳定,使机械臂的操作过程更加贴近生物臂。该方法理论明确,实现过程简单,实时性好,可应用于空间机器人、地面探索机器人及工业机器人等领域,具有广泛的实用价值和意义。目前该方法已在某航天技术研究院空间机械臂原理样机中得到成功的应用。该方法仍存在约±4 N的力补偿误差,和约±0.5 N•m的力矩补偿误差,需要加入预测补偿机制,以减小包括机械臂运动学建模误差、F/T传感器测量误差、计算过程舍入误差和机械振动等带来的影响,进一步改善大范围柔顺控制效果,这也是下一步要探讨的重点。
| [1] | 叶平, 何雷, 宋爽, 等. 空间机械臂地面微重力混合模拟方法研究[J]. 机器人, 2013, 35(3):299-305, 312. YE Ping, HE Lei, SONG Shuang, et al. A hybrid method for microgravity simulation of space robotic manipulator[J]. Robot, 2013, 35(3):299-305, 312. |
| [2] | ARNO H A, EDSKO E G, FRANS C T, et al. Freebal:dedicated gravity compensation for the upper extremities[C] //IEEE 10th International Conference on Rehabilitation Robotics.Noordwijk, Holland, 2007:804-808. |
| [3] | 周啟航. 空间机械臂地面零重力模拟系统设计及分析[D]. 哈尔滨:哈尔滨工业大学, 2012:1-10. ZHOU Qihang. The research of space manipulator zero-gravity simulation system[D]. Harbin:Harbin Institute of Technology, 2012:1-10. |
| [4] | DELUCA A, PANZIERI S. A simple iterative scheme for learning gravity compensation in robot arms[C] //36th Associazione Nazionale Italiana Per L'Automazione Annual Conf (Automation).Genova, 1992:459-471. |
| [5] | LUCA A D, PANZIERI S. An asymptotically stable joint PD controller for robot arms with flexible links under gravity[C] //31st IEEE Conference on Decision and Control.Tucson, USA, 1992:325-326. |
| [6] | KELLY R. PD control with desired gravity compensation of robotic manipulators:a review[J]. The International Journal of Robotics Research, 1997, 16(5):660-672. |
| [7] | REN C L, CHUN Y Y, YI W P. Gravity compensation and compliance based force control for auxiliarily easiness in manipulating robot arm[C] //8th Asian Control Conference (ASCC).Kaohsiung, China, 2011:1193-1198. |
| [8] | 杨振. 基于阻抗控制的机器人柔顺性控制方法研究[D]. 南京:东南大学, 2005:1-3. YANG Zhen. An overview on compliance control of robot based on impedance control[D]. Nanjing:Southeast University Press, 2005:1-3. |
| [9] | CRAIG J J, RAIBERT M H. A systematic method of hybrid position/force control of a manipulator[C] //Computer Software and Applications Conference (COMPSAC 79).Piscataway, USA, 1979:446-451. |
| [10] | CHUNG J C H, LEININGER G G. Task-level adaptive hybrid manipulator control[J]. The International Journal of Robotic Research, 1990, 9(3):63-73. |
| [11] | CONNOLLY T H, PFEIFFER F. Neural network hybrid position/force control[C] //International Conference on Intelligent Robots and Systems.Piscataway, USA, 1993:240-244. |
| [12] | XU Yangsheng, PAUL R P. Robotic instrumented complaint wrist[J]. Journal of Engineering for Industry, Transactions of the ASME (American Society of Mechanical Engineers), 1992, 114(1):120-123. |
| [13] | HOGAN N. Impedance control:an approach to manipulation[C] //1984 American Control Conference.San Diego, USA, 1984:304-313. |
| [14] | MATSUEDA T, KURAOKA K, GOMA K, et al. JEMRMS system design and development status[C]//National Telesystems Conference. Atlanta, USA, 1991:391-395. |
| [15] | 刘福才, 高娟娟, 王跃灵. 重力对空间机械臂运动控制的影响[J]. 高技术通讯, 2012, 22(9):944-950. LIU Fucai, GAO Juanjuan, WANG Yueling. Effects of gravity on the motion control of a space manipulator[J]. High Technology Letters, 2012, 22(9):944-950. |
| [16] | 蔡自兴. 机器人学[M]. 北京:清华大学出版社, 2009:41-45. CAI Zixing. Robotics[M]. Beijing:Tsinghua University Press, 2009:41-45. |
| [17] | 陈锋, 费燕琼, 赵锡芳. 机器人的阻抗控制[J]. 组合机床与自动化加工技术, 2005, 2(12):46-47, 50. CHEN Feng, FEI Yanqiong, ZHAO Xifang. The impedance control method for robots[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2005, 2(12):46-47, 50. |



