2. 北京交通大学 计算机与信息技术学院, 北京 100044;
3. 北京交通大学 北京现代信息科学与网络技术北京市重点实验室, 北京 100044;
4. 中国科学院 软件研究所, 北京 100190
2. School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China;
3. Beijing Key Laboratory of Advanced Information Science and Network Technology, Beijing Jiaotong University, Beijing 100044, China;
4. Institute of Software, Chinese Academy of Sciences, Beijing 100190, China
图像分割作为计算机视觉和人工智能领域中一项意义重大而又艰巨的研究工作,众多国内外学者对此展开了深入广泛的研究,提出了很多算法,现有算法大致可以分为: 边缘检测算法、聚类算法和区域算法。其中,基于聚类算法的图像分割算法是图像分割领域中一类极其重要且应用广泛的算法。该类算法将图像分割问题转化为根据像素特征对像素进行分类的过程,使得在同一类中的像素尽可能的相似,而不同类中的像素则尽可能的不相似。
所谓聚类就是将具有相似性质的事物区分并加以分类,而图像分割问题恰好是将图像的像素集进行分类的问题,因此,人们很自然地将聚类分析应用于图像分割。早在1979年,Coleman和Anderews就提出采用聚类算法进行图像分割[1],同时也有学者使用聚类算法进行预分,然后再基于高低精度距离重构泡的方法对图像进行分割[2]。K-均值作为一种简单有效的聚类算法也在图像分割中得到了广泛的应用。最初的基于K-均值的图像分割算法只考虑特征向量,而忽略了像素间的空间位置关系,因此,会造成在空间位置上很接近的像素点在特征空间中却相距很远。为了有效地消除这种情况,又出现了对K-均值分割方法的改进研究,从而产生了一系列基于空间位置约束的K-均值图像分割算法研究[3],不仅考虑像素的视觉相似性,还考虑了像素的空间邻域信息。基于K-均值的图像分割算法虽然是一种简单高效的算法,仍存在很多问题。首先需要预先知道聚类中心的数目,虽然大多情况下能够得到很好的分割效果,但分割结果对初始值敏感,算法鲁棒性不强。实际上,基于K-均值的聚类通常将聚类问题转化为一个优化问题,然后采用各种优化算法求解。在实际应用中,由于样本数据分布的多样性,目标函数往往比较复杂,采用传统的优化算法很难获得问题的最优解。因此,近似最优算法以及寻找局部最优解的聚类算法成为人们研究的热点。人工鱼群算法作为一类智能优化算法[4, 5],其主要特点是群体搜索策略以及群体之间的信息交换,对目标函数的性态没有苛刻要求,具备全局寻优的能力,求解不依赖于梯度信息,因而特别适用于大规模复杂问题的求解,在实际中具有广泛的应用前景[6, 7]。因此,本文提出了一种基于人工鱼群的图像自动分割算法。
目前已有学者提出了基于人工鱼群的分割算法,文献[8]提出了一种基于人工鱼群的二维Otsu阈值分割,成功地将鱼群算法应用到了灰度图像的分割。该算法通过模拟鱼群的聚群、追尾、捕食等行为来找到实物浓度最大的个体,从而找到最好的分割阈值。文献[9]则对含噪声图像使用小波变换来进行小波域抑噪预处理后,使用鱼群算法来寻找最优阈值进行阈值分割,也取得了比较好的分割效果。文献[10]则采用人工鱼群算法对K-均值聚类进行初始化,从而克服K-均值聚类对初始化的依赖。但是,目前鱼群算法的应用都是针对灰度图像分割的应用。本文提出了利用鱼群算法这种群体智能算法针对彩色图像的特征空间进行聚类,同时在聚类过程引入动态小生境的概念,通过小生境内部个体之间以及不同小生境之间的自组织,自动确定聚类类别数目,并对初始值不敏感。实验结果表明所提算法能够很好地根据彩色图像的特征空间对图像进行自动分割。
1 人工鱼群算法人工鱼群算法是20世纪初提出来的一种智能群体寻优算法[4]。该方法通过模仿鱼类行为方式,模仿鱼群的聚群、追尾、捕食等行为来进行寻优,其具体步骤如图 1所示。鱼群中个体根据视野范围内的个体食物浓度选择合适的行为以最大步长范围内的距离进行活动。
 |
| 图 1 人工鱼群基本操作步骤 Fig. 1 The basic operation of the artificial fish swarm |
人工鱼群算法初始种群给定后,每个人工鱼就是一个初始聚类中心,在搜索空间中以visual为视野范围观察周围个体的适应度和拥挤情况,并根据情况来选择聚群和追尾行为。若找到一个比当前适应度大的行为方向,则以小于最大步长step的长度向此方向进行游动,当都不满足2种行为的条件移动的时候,则选择捕食行为。算法中所使用的聚群、追尾、捕食等行为具体操作如下:
1) 聚群行为: 设人工鱼当前状态为(zi,J),个体在特征空间中以visual为视野范围,设在其视野范围内有nf个个体,这些个体的中心位置为(zc,Jc)。若Jc/nf>δ×Ji(δ表示拥挤度数),则说明其视野范围内个体中食物浓度较高并且还不太拥挤,则该个体向该个体伙伴中心位置方向,即(zc,Jc)方向以小于最大步长step前进一步。
2) 追尾行为: 设人工鱼当前状态为(zi,Ji),在其搜索空间内寻找一个适应值最大的个体(zj,Jj),并在其视野范围内寻找同伴的个数nf,若满足Jj/nf>δ×Ji,说明最大个体附近食物浓度较高,且不拥挤,则沿着此最大个体方向移动。
3) 捕食行为: 此行为为追尾和聚群行为的缺省行为,设人工鱼当前状态为(zi,Ji),在个体搜索范围内即半径为visual范围内向任意方向(zj,Jj)尝试移动,若该位置具有比当前位置较高的食物浓度,则向此方向随机大小移动一步,否则继续尝试。若达到设定的最大尝试次数还未找到一个比当前位置适应值更高的方向则执行随机行为。
4) 随机行为: 随机行为是在以上3种行为均不满足时执行的缺省行为,就是在其视野范围内随机方向移动一步。
2 基于动态小生境的人工鱼群算法本节提出了一种基于动态小生境人工鱼群算法(DNAF),该算法将彩色图像的颜色空间作为特征空间,使用鱼群算法实现了图像的自动分割,其具体步骤如图 2所示。为了克服传统聚类算法中需要指定聚类中心的数目的问题,DNAF算法使用了动态小生境技术,在每一代的进化后都根据鱼群的在特征空间的分布情况,将鱼群自动分为相应数目的小生境,然后继续下一代的进化。该算法中所获得的鱼群的小生境个数即为图像分割问题的类别数。
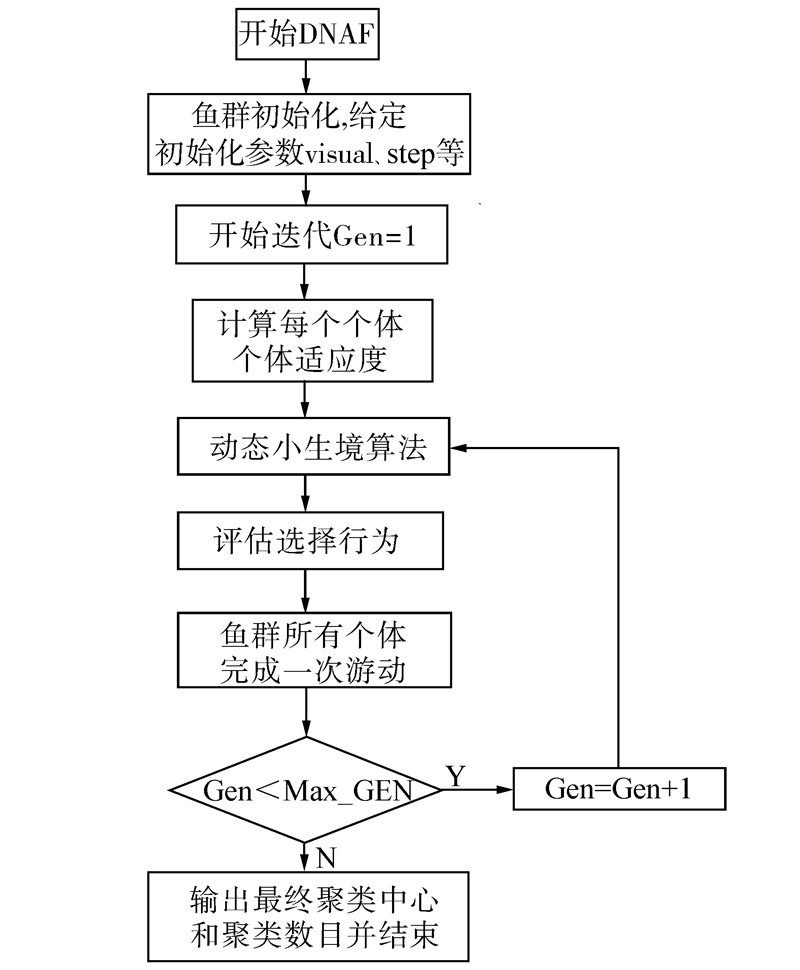 |
| 图 2 DNAF算法流程图 Fig. 2 Flowchart of DNAF algorithm |
在算法中,本文采用实数编码方式对分割中心进行编码,一个人工鱼描述一个类别中心,即每个人工鱼为长度N + 1的实数序列(zj,jj):
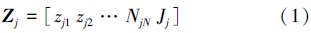
式中: N为图像特征空间的维数,zj为人工鱼在特征空间的位置,Jj为人工鱼的食物浓度,即目标函数值。种群规模为P的初始鱼群是随机生成的,本文随机选取P个不同的像素点作为初始鱼群。
2.2 食物浓度函数本节引入一种新的聚类算法的目标函数,通过该目标函数,可以将传统的基于聚类算法的图像分割转化为多峰函数求极值问题,目标函数峰值的个数即为分割问题的区域数,峰值所对应的变量值即为分割问题的区域中心。
令X={x1,x2,…,xn}为N维图像特征集,K为类别数,即图像中的区域数,则分割目标就是寻找一系列ci使得目标函数Js(z)值最大,且:
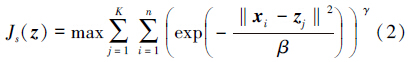
式中:Z=(Z1,Z2,…,Zk),β为标准化参数:

则人工鱼群的食物浓度为
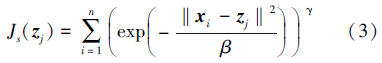
文献[11]指出了目标函数中的γ决定目标函数峰的位置和个数。本文采用文献[11]提出的CCA算法估计γ。在获得γ的估计值之后,函数Js(zj) 则转变为一个多峰函数,且其峰的个数与特征集X={x1,x2,…,xn}中的类别数相同。因此,通过此目标函数即可将图像分割问题转化为一个多峰函数求解问题,通过估计函数 Js(zj) 的峰的个数和峰值来求解分割问题的区域数和区域中心,Js(zj) 局部极值的个数即为所求分割的区域数,局部最优值即为区域中心。
2.3 自适应动态小生境人工鱼群初始化后或者每一次迭代之后,根据人工鱼群在特征空间中的分布情况将每一个个体分配到相应的小生境中,具体的算法描述如下。
1)计算每个个体的食物浓度;
2)找到最大个体,以此个体为中心初始小生境半径范围内的所有个体划分到以此个体为中心的小生境内;
3)在没有被划分的个体中寻找适应度最大的个体,进行操作2),直至所有个体都被划分到各自所在的小生境内。
伪代码如表 1所示。
| 输入: | 迭代次数为第t代时人工鱼群Popt |
| 鱼群大小为P,小生境半径为σ | |
| 根据鱼群的食物浓度将鱼群进行降序排序 | |
| v(t)=0表示真实小生境个数 | |
| u(t)=0表示候选小生境个数 |
| For i = 1 to p do |
| If第i个体未被划分到任何小生境 |
| u(t)=u(t)+1 |
| N(u(t))=1(第u(t)个小生境中的个体数目) |
| For j =i+1 to P do |
| If (d(i,j)<σ)且第j个体未被划分 |
| 第j个个体加入第u(t)个小生境中 |
| N(u(t))=N(u(t))+1 |
| End If |
| End for |
| If (N(u(t))>1)则v(t)=v(t)+1 |
| 标记第i个个体为第v(t)小生境的代表个体 |
| End If |
| End If |
| End For |
通过表 1给出动态小生境算法即可将第t代人工鱼群Popt划分为一系列的小种群。将确定的一系列的候选小生境的集合分为2类,一类是种群中个体数目大于1的小生境称为真正的小生境,记为Sit; 另一类则是只有一个个体的小生境,将这些单个体小生境合并为一个小生境S*t。这样,Popt即被划分为v(t)个真正的小种群S1t,S2t,…,Sv(t)t和一个复合小种群S*t,即
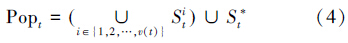
给定一个迭代次数,每一个个体按照基本的鱼群算法进行迭代寻优,在每一次迭代结束后重复2.3中的动态小生境的划分,真正的小生境的代表个体即为分割问题的区域中心。随着迭代次数的增加,最后得到的小生境个数就是图像分割的区域总数,小生境中代表个体即为分割区域的中心。
3 实验结果与分析为了验证本文所提DNAF算法的分割性能,在本节中将小生境遗传算法SCGA[12]、K-均值、模糊C-均值[13]和DNAF应用于彩色图像的分割,实验证明本文的算法可以有效的对图像进行分割。
实验中采用如图 3所示的3幅图像(源自Berkeley图像数据库)。由于K-均值和模糊C-均值算法需要预先知道划分的类别数,在实验中将其设为图像中的真实类别数。为了直观的比较3种算法的性能,进行了多次试验结果进行平均(通过投票确定最终的分割区域数,并仅对正确分割的结果进行平均),在图 4~6中给出4种算法的最终分割结果。由图可见,本文所提DNAF算法可以有效地对图像进行分割,并且可以自动地确定分割的类别数,算法自动获得的分割区域数如表 2所示。由于本文提出的算法主要是通过鱼群的游动实现的,在每一代的进化时每一个个体都要进行一次行为的判断,并且每一个个体都需要根据周围特征点分布进行计算得到食物浓度,因此本算法时间复杂度为O(nm),其中为n初始化鱼群个体数目,m为图像像素点的个数。
 |
| 图 3 实验使用的原始图像 Fig. 3 The original image used in the experiment |
 |
| 图 4 4种算法对教堂图像的分割结果 Fig. 4 The segmentation results for the church obtained by four algorithms |
 |
| 图 5 4种算法对飞机图像的分割结果Fig. 5 The segmentation results for the plane obtained by four algorithms |
 |
| 图 6 4种算法对海星图像的分割结果 Fig. 6 The segmentation results for the starfish obtained by four algorithms |
为了进一步验证算法的有效性,采用文献[14]中的F(I)、F′(I) 和Q(I)对算法性能进行比较,其值越小则意味着对图像的分割结果越好。表 3中给出了对实验中所采用的4幅图像分割结果的F(I)、F′(I) 和Q(I)。由表 3可见,DNAF算法的性能优于其他2种算法,对图像的分割结果获得了较小的F(I)、F′(I) 和Q(I)。
| 算法 | Image | F(I) | F | Q(I) |
| SCGA |
| ||||||||||||
| K-均值 |
| ||||||||||||
|
模糊 C-均值 |
| ||||||||||||
| DNAF |
|
本文提出了一种基于DNAF算法的图像分割算法,该算法通过对鱼群的不断进化,可以同时获得分割问题的区域数和区域中心。由于该算法并不需要预先对分割区域数进行设定,因此,在实际中将具有更广泛的应用前景。DNAF分割算法采用一种更为简便的个体描述方式,即每个个体即代表一个区域中心,通过动态地对鱼群划分为几个小生境而获得分割的区域数。通过实验仿真可见,所提DNAF算法可以有效地实现对图像的自动分割。
| [1] | COLEMAN G B, ANDREWS H C. Image segmentation by clustering[J]. Proceedings of the IEEE, 1979, 67(5):773-785. |
| [2] | 阳春华, 杨尽英, 牟学民, 等. 基于聚类预分割和高低精度距离重构的彩色浮选泡沫图像分割[J]. 电子与信息学报, 2008, 30(6):1286-1290. YANG Chunhua, YANG Jinying, MOU Xuemin, et al. A segmentation method based on clustering pre-segmentation and high-low scale distance reconstruction for colour froth image[J]. Journal of Electronics & Information Technology, 2008, 30(6):1286-1290. |
| [3] | ZHANG Jingdong, JIANG Wuhan, WANG Ruichun, et al. Brain MR image segmentation with spatial constrained K-mean algorithm and dual-tree complex wavelet transform[J]. Journal of Medical Systems, 2014, 38(9):93. |
| [4] | 李晓磊. 一种新型的智能优化方法——人工鱼群算法[D]. 杭州:浙江大学, 2003:10-15.LI Xiaolei. A new intelligent optimization method-artificial fish school algorithm[D]. Hangzhou, China:Zhejiang University, 2003:10-15. |
| [5] | HUANG Zhenhuang, CHEN Yidong. An improved artificial fish swarm algorithm based on hybrid behavior selection[J]. International Journal of Control and Automation, 2013, 6(5):103-116. |
| [6] | EI-SAID S A. Image quantization using improved artificial fish swarm algorithm[J]. Soft Computing, 2014, 24(8):221-232. |
| [7] | LIU Qing, ODAKA T, KUROIWA J, et al. Application of an artificial fish swarm algorithm in symbolic regression[J]. IEICE Transactions on Information and Systems, 2013, 96-D(4):872-885. |
| [8] | 潘喆, 吴一全. 二维Otsu图像分割的人工鱼群算法[J]. 光学学报, 2009, 29(8):2115-2121. PAN Zhe, WU Yiquan. The two-dimensional Otsu thresholding based on fish-swarm algorithm[J]. Acta Optica Sinica, 2009, 29(8):2115-2121. |
| [9] | 范玉军, 王冬冬, 孙明明. 改进的人工鱼群算法[J]. 重庆师范大学学报:自然科学版, 2007, 24(3):23-26. FAN Yujun, WANG Dongdong, SUN Mingming. Improved artificial fish-school algorithm[J]. Journal of Chongqing Normal University:Natural Science Edition, 2007, 24(3):23-26. |
| [10] | 楚晓丽. K-means聚类算法和人工鱼群算法应用于图像分割技术[J]. 计算机系统应用, 2013, 22(4):92-94. CHU Xiaoli. K-means clustering algorithm and artificial fish swarm algorithm applied in image segmentation technology[J]. Computer Systems and Applications, 2013, 22(4):92-96. |
| [11] | YANG M S, WU K L. A similarity-based robust clustering method[J]. IEEE Transactions on Pattern Analysis Machine Intelligence, 2004, 26(4):434-448. |
| [12] | LI Jianping, MARTON E B, PARKS GY T, et al. A species conserving genetic algorithm for multimodal function optimization[J]. Evolutionary Computation, 2002, 10(3):207-234. |
| [13] | BEZDEK J C, CHRISTIAN J. Fuzzy mathematics in pattern classification[D]. New York City:Cornell University, 1973, 142-147. |
| [14] | BORSOTTI M, CAMPADELLI P, SCHETTINI R. Quantitative evaluation of color image segmentation results[J]. Pattern Recognition Letters, 1998, 19(8):741-747. |



