2. 石家庄铁道大学 电气与电子工程学院, 河北 石家庄 050043;
3. 清华大学 智能技术与系统国家重点实验室, 北京 100084
2. College of Electrical and Electronic Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;
3. Key Laboratory of Intelligent Technology and Systems, Tsinghua University, Beijing 100084, China
同时定位与地图创建(simultaneous localization and mapping,SLAM)是移动机器人研究领域中一个关键技术[1],是在未知环境中通过自定位过程获取周围环境信息,并在行进过程中逐步构建周围环境的增量式地图,同时不断地重复观测已构建的地图来消除不确定因素,进而完成自身位姿的精确估计[2]。因此,机器人位姿估计和地图构建之间的相互依赖使SLAM问题变得极富挑战性,需要在高维空间中搜索解决方法[3]。
目前,国内外的研究重点侧重于基于特征地图的定位方法[4],即通过存储在地图中的环境特征与抽象所感知真实环境的特征是否匹配及相对于机器人SLAM的位置来确定机器人的当前位姿,因此环境地图的表示方式是否合适以及环境特征提取是否准确,直接影响环境特征匹配的效率,进而影响机器人定位和地图构建的准确性和实时性; 测距传感器由于具有数据处理简单、实时性高和鲁棒性好等优点,得到了广泛的应用; 基于测距式传感器的机器人定位和地图构建的基本思想是通过融合传感器信息,把自身与参照点(如障碍物、环境特征等)及其相互关系的距离信息和方位信息在线抽象描述为全局地图信息。
基于测距式传感器机器人SLAM主要从3方面考虑: 环境特征的提取方法、地图的表示方式和解决SLAM问题的核心算法[2]。本文总结目前流行的基于测距式传感器的SLAM方法,从以上3方面进行了归类和比较,指出需要解决的关键问题,并根据已有的研究成果提出未来的研究方向。
1 典型传感器类型及其作用根据机器人所携带传感器在SLAM系统中的主要作用,传感器大致可分为两大类,一类是本体传感器(也称内部传感器),如里程计、陀螺仪、指南针、速度或加速度计等; 另一类是外部传感器,如激光雷达、超声波、红外线、微波雷达、kinect[5],机器人通过外部传感器可以获得真实环境特征的抽象描述及距离信息或图像深度信息。基于测距式的SLAM主要框架是采用本体传感器和外部传感器相融合的定位方法,利用本体传感器来实现机器人航迹推算,通过外部传感器(一种或多种)抽象获得的外部环境特征及其距离信息与已构建环境地图的特征匹配,消除航迹推算的累积误差,获得当前机器人的位姿偏差,并不断修正机器人自身位姿,构建增量式的环境地图。
2 环境模型及测距式传感器特征提取真实环境的抽象描述也称为地图构建,即用点和线或栅格的集合近似表达真实环境,是将真实环境中连续场景表示成2-D区段,是移动机器人SLAM的一个重要环节[6, 7]。地图中环境特征表征的准确与否直接影响机器人定位和构建地图的精确性,因此环境特征的表示要注重特征的鲁棒性和稳定性。测距式传感器SALM的环境模型主要有2类,基于特征的地图和密集型地图(栅格地图),前者主要应用于稀疏障碍物或结构化环境,将环境特征作为路标信息,后者主要应用于非结构化环境。在平面坐标系中机器人根据2条相交的直线就可以完成自定位,由于环境中存在诸如角、线的特征较多,而从测距式传感器检测到的原始数据中提取这些特征相对容易,其存储与匹配也简洁方便,因此采用角、线描述环境成为机器人SLAM问题中最常用的特征描述方式。针对缺少角、线特征的环境,文献[6, 8, 9]通过提取天花板的角、线特征来完成机器人定位; 此外,根据机器人所在环境的特点,提取具有独特信息的特征作为路标信息,文献[10, 11, 12]提取环境中圆作为定位路标信息,文献[6]提取环境中矩形特征作为定位路标信息。随着环境的复杂性越来越高,对环境二维建模不能满足需要,文献[13, 14]等提取环境三维特征作为定位路标信息。栅格地图模型是根据测距传感器的原始数据获得障碍物占据栅格情况,从而构建环境地图[2]。
测距式传感器采集真实环境的数据是点的集合,如何对这些离散的点处理获得环境的抽象描述,即局部地图,很多文献采用了Hough变换的方法进行局部地图的构建,但其计算量非常大,很难保证局部地图构建实时性的要求,文献[15]比较详细地分析比较了11种数据点提取特征直线的算法,其中以数据分割拟合(split-and-merge)算法较优,因此该算法得到了广泛应用; 此后,研究者在分析总结上述算法的基础上,对这些算法做了改进,也提出了很多不同的特征提取算法,如文献[16]通过建立角点函数来衡量扫描点是角点特征的程度,利用非极大值抑制方法去除干扰信息来提取环境的角点特征,文献[17]根据split-and-merge算法思想,采用模糊聚类算法分割数据,利用最小二乘法拟合。
直线参数使线段分割的鲁棒性和线段提取的精度得到了很大提高,也显著提高了算法效率。此外,有研究者将比较成熟的优化算法应用到环境特征的提取,如文献[18]将自组织竞争学习神经网络(self-organizing feature mapping,SOM)方法用于激光雷达数据的处理,提取更加精确的环境线段、角点等特征,提高了算法的计算效率以及分类性能得到进一步的提高。也有研究者采用卡尔曼滤波对环境的线段等特征进行提取,不仅对线段特征的误差标准等概率特性进行较好地描述和更新,而且受传感器的非线性影响也较小。
3 基于测距式传感器SLAM常用方法目前,未知环境中机器人利用测距式传感器的距离信息完成SLAM任务,其基本思想是通过寻找当前局部环境地图与已获得的增量式全局环境地图间的对应关系,减少航迹推算误差造成的移动机器人定位的不确定性[19],获得尽可能精确的机器人当前位姿信息,完备全局环境地图。目前主要方法可分为基于贝叶斯理论的概率推理定位算法和基于矩阵分解的定位算法两大类。前者把概率理论应用到移动机器人定位过程中,即在机器人每个可能的位置设置一种概率值,根据机器人运动过程中测距式传感器感知到的新环境距离信息更新机器人可能位置的概率值,从而减少机器人位置不确定性。其实质是把移动机器人SLAM问题认为是贝叶斯评估过程,通过融合内部传感器输入数据和外部传感器观测数据,完成移动机器人隐式位姿的预测及更新,使其隐式位姿状态信度达到最优。比较典型的方法有: 基于扩展卡尔曼滤波(extended kalman filter,EKF)和基于粒子滤波(particle filter,PF)SLAM。后者通过分析数据矩阵的特点,把矩阵分解出能反映原矩阵的某些特征的因式矩阵,通过回归计算因式矩阵获得当前机器人的位姿和环境信息,完成SLAM任务。
3.1 基于EKF的SLAM定位方法EKF是将非线性模型(运动模型和观测模型)在状态向量的邻域内泰勒展开,并取其一阶或二阶项近似表示机器人的运动模型与观测模型。该方法的基本思想是通过对包含移动机器人与环境特征之间的关系以及机器人运动模型、观测模型不确定性信息的雅可比矩阵的迭代过程,完成误差协方差矩阵和增益矩阵的递推计算。正常情况下,雅可比矩阵是单调递减且收敛的,因此,对雅可比矩阵的处理是EKF的核心。
基于扩展卡尔曼滤波器的SLAM方法是通过增量评估移动机器人位姿和环境特征位置的联合后验概率来估计机器人位姿和构建地图,是一个循环迭代地估计与校正过程。即机器人根据运动模型估计其新位置,根据机器人观测模型估计其可能观测到的环境特征的距离信息; 计算估计的观测值间与实际的观测值之间的误差,利用协方差计算卡尔曼滤波增益参数,并利用该参数对机器人的估计位置校正; 将新观测到的环境特征信息加入地图,逐步完成增量式环境地图的构建。在估计与校正过程中若系统状态的协方差较大,则用观测值校正,使系统偏差变小; 若观测协方差较大,则认为观测值不可靠,对观测值做轻微校正[20]。
以EKF理论为基础的SLAM的方法存在一些固有的缺陷。缺陷一是非线性误差的存在[2],由于EKF算法在估计点处通过泰勒展开式对非线性系统进行局部线性化,舍去了高阶项,虽然简化了问题,但使系统产生了截断误差。如系统非线性程度较高时,由于系统无法满足上述线性化假设而产生很大的误差,从而造成系统不收敛的严重后果,因而基于EKF的SLAM的精度和鲁棒性受到影响。针对EKF线性化存在的误差,研究者在如何提高SLAM问题的精度上展开了研究,提出了许多改进算法。如文献[21]提出迭代扩展卡尔曼滤波算法(
iterated extended Kalman filter,IEKF),结合激光雷达传感器采集的外部环境特征信息,在测量更新阶段多次迭代滤波估计值,从而减少由于泰勒展开局部线性化带来的截断误差,提高了SLAM的定位精度,但是其缺点是由于迭代次数的增加,计算量会增大; 文献[22]针对EKF中观测噪声方差估计不准确导致滤波器性能下降甚至发散的问题,将模糊卡尔曼滤波技术应用于基于声呐的移动机器人的定位中,提出了根据信息方差理论值和实际值的一致程度在线调整观测噪声方差的自适应调节算法,解决了系统观测噪声水平不确定的问题,其性能优于EKF; 文献[23]在光电系统中利用差分方式实现非线性函数线性化的EKF算法,这种方法无需计算复杂的雅克比阵,且能得到更好的定位跟踪精度; 文献[2, 24]提出将随机梯度下降法引入SLAM问题,达到最小化系统非线性误差的影响,但是系统的收敛速度变慢了。
基于扩展的卡尔曼滤波器方法得到机器人领域广泛地接受,但随着SLAM问题研究的深入,出现了计算复杂度和数据关联问题,即缺陷二。协方差阵的引入是EKF的最大特点,对协方差阵的计算也是该算法的核心。当环境中的不确定因素和环境特征增加时,协方差阵的元素平方级增加,计算量复杂度为O(K2)(K为特征数目)[25],即使在某一刻只观测到一个特征,整个协方差阵元素都必须更新,计算量急剧增加。此外,机器人与环境特征及环境特征与环境特征之间的交叉相关性进一步增加了计算复杂度。文献[26]采用FPGA技术和并行处理流程完成多个特征同时匹配过程,提高了特征匹配效率; 文献[27]采用表示环境特征之间相对位置的相对地图代替绝对地图,解决了环境特征之间的相关问题; 文献[28]用稀疏化信息矩阵代替协方差矩阵,即稀疏扩展信息滤波方法,使更新时间变为常数,不随特征的增加而增加。
另外,基于EKF的SLAM算法存在2个较难解决的问题: 1)假设观测量与环境特征的数据关联为已知,即认为它们之间必存在数据关联,一旦观测值和环境特征之间出现微小的关联错误,将会导致EKF滤波器发散而使SLAM过程失败。2)机器人状态向量无法表征机器人的历史路径,无法解耦地图信息与机器人状态的关系,当环境地图增大时导致计算量急剧增大。因此,该方法不适合大规模环境和动态环境的SLAM。
目前,在EKF的SLAM方法的基础上,提出了一些改进算法,如无迹变换的UKF-SLAM、容积卡尔曼滤波SLAM、平方根容积卡尔曼滤波SLAM等。通过不同的方法获得SLAM的后验概率密度,提高了定位精度。
3.2 基于PF的SLAM定位方法PF是20世纪90年代中后期发展起来的一种比较新的滤波算法。文献[29]将PF与机器人运动及感知的概率模型相结合,提出了PF的定位方法; 其主要思想是用多个滤波器来估计机器人的各个可能位置的概率,利用观测对每个滤波器进行加权处理,使机器人最有可能位置的概率越来越大[30]。在实际应用中,基于PF的SLAM方法是用一组相关权重的随机样本集合,以及基于这些样本的估计来近似表征后验概率密度函数,采用样本均值代替积分运算来获得状态最小方差估计的过程。
SLAM主要任务是位姿估计和地图构建,2者之间又存在相互依赖的关系,这使基于PF的SLAM问题变得非常复杂。文献[31]提出了SLAM问题的一种有效解决方案,即后验概率估计的处理方法,其基本思想是通过Rao-Blackwellized将SLAM问题分解为轨迹估计过程与地图估计过程。先用粒子滤波器估计移动机器人的运动轨迹,再用卡尔曼滤波估计环境地图,从而将SLAM问题转化为低维估计问题[32, 33]。
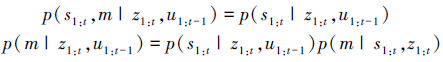
式中: s1:t为移动机器人轨迹,u1:t-1为里程计测量,m为观测z1:t得到的地图。
在已知s1:t和z1:t的条件下,可以得到地图的后验概率p(m|s1:t,z1:t),而建图的Rao-Blackweiiized通过PF方法得到机器人潜在轨迹的后验概率p(s1:t|z1:t,u1:t-1),并为每个粒子分配一个合适的“粒子地图”,该地图是在给定了由相应粒子所表示的s1:t和z1:t条件下建立; 换言之,机器人在未知环境中循环运行一圈,每个粒子都估计机器人的轨迹,并相应保留一个“粒子地图”,该地图根据轨迹估计不断更新,即根据已知位姿构建地图。
常用的Rao-Blackweiiized粒子滤波器建图过程主要有以下4个步骤:
1)采样,子代粒子是从当前粒子中根据建议分布q采样得到;
2)每个粒子赋重要性权值: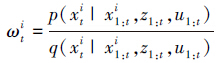
3)重采样,其包含2层意思: 1)用有限粒子近似一个连续分布,2)重采样允许在真实分布与建议分布有差异的情况下使用粒子滤波器;
4)地图估计,通过已知位姿更新每个粒子的“粒子地图”。
在Rao-Blackwellized粒子滤波的基础上,Montemerlo等[33]提出FastSLAM算法,与基于EKF的SLAM方法不同,其用不同的粒子表征机器人的历史路径,能够解耦地图特征信息与机器人状态信息; 即将SLAM问题看成机器人行进轨迹的PF估计和机器人位姿估计上环境特征位置卡尔曼滤波估计过程。粒子滤波器中每个粒子代表机器人的一条可能的行进轨迹,利用观测值计算各个粒子的权重。具体到每个粒子,机器人的行进轨迹是确定的,环境特征标志之间相互独立,特征标志的观测信息仅与机器人的位姿有关。每个粒子采用N个卡尔曼滤波器分别估计地图中N个特征的位置。对于FastSLAM算法的复杂度,如果采用K个粒子实现SLAM,总共有KN个卡尔曼滤波器,其复杂度为O(KN),利用一些算法(如树型数据结构)进行优化,其复杂度可以进一步减小到O(KlogN)[25]。针对数据关联错误,通过减小该粒子的权重来降低关联错误对定位的影响[34]。FastSLAM方法的另一个优点是相比较于卡尔曼滤波定位方法,可以较好地解决机器人的非线性和非高斯运动问题。
以PF为理论基础的FastSLAM算法,FastSLAM1.0和FastSLAM2.0 有2个版本。FastsLAM1.0用粒子滤波器估计移动机器人位姿,用EKF估计环境特征。但其直接把SLAM过程模型作为采样粒子重要性函数,从重要性函数抽取的样本不能准确表达真实的后验概率密度函数,当环境观测值噪声较小时,易造成严重的样本退化问题和定位精度下降。FatSLAM2.0用EKF递归估计机器人位姿,构建融入机器人前期位姿信息的高斯分布函数为重要函数,缓解了样本退化问题,提高了算法的精度。针对测距式传感器,如激光雷达,影响粒子滤波器性能主要因素是建议分布的选择和选择性采样。由于激光扫描仪的精度导致了峰值很高的似然函数,与大部分粒子滤波器选用里程计运动模型p(st|st-1,ut-1)为建议分布不同,其选用高斯建议分布。这样既考虑了最近观测数据,也为高效采样提供了可能,其结果比用里程计运动模型更具有确定性[3]。在重采样过程中,低权值粒子被高权值粒子代替,这有可能删除较好的粒子。在构建图过程中,尤其在嵌套环路环境中,外层环路构建图中需要的粒子并不一定是内层环路高权值的粒子。文献[35]介绍了一种衡量有效粒子数的方法来评价当前粒子集能否表征后验估计,只有在需要时重采样才被执行,降低了较好粒子被替换的几率。文献[36]通过迭代卡尔曼滤波方法融入新的观测值,用复制样本与剔除样本的线性组合降低样本退化及样本贫化。
综上所述,FastSLAM算法获取建议分布函数与估计环境特征位置依然是基于EKF理论,同样存在样本退化问题。因此,FastSLAM算法发展趋势主要从以下2方面考虑:
1)改进机器人位姿路径评估的粒子滤波。改进建议分布使其近似真实分布; 改进重采样策略;改进自适应机制,如自适应粒子数目、自适应重采样技术及自适应运动模型。
2)改进环境特征评估的EKF。采用混合卡尔曼滤波器、UT变换的无迹卡尔曼滤波和无迹粒子滤波等方法提高计算的有效性。
3.3 基于矩阵奇异值分解(SVD)的SLAM方法矩阵的分解因式是原矩阵特殊存在形式,能明显反映出原矩阵的某些特征,从而为系统分析提供有效的计算方法和理论分析根据。矩阵SVD是一种应用比较广泛的分解形式。在基于卡尔曼滤波定位算法中,协方差矩阵对舍入误差较敏感,特别是高维的复杂系统,在迭代过程中经常出现矩阵病态问题,导致协方差矩阵失去对称性和正定性,从而导致算法失效。文献[37, 38]通过协方差矩阵迭代分解计算,避免了协方差阵的求逆运算,减少了计算量,提高了算法的稳定性。文献[39]通过激光雷达获得障碍物和方向距离信息,求取直线交点坐标作为路标,建立路标的相关矩阵,由直线、路标和相关矩阵构成局部地图,通过匹配局部地图与全局地图找出最优的关联匹配,利用SVD获得路标在全局坐标系和局部坐标系下的关系,完成地图的更新。文献[40]将测距式SALM问题看成距离信息矩阵SVD的过程,通过把距离矩阵SVD得到包含有路标信息和机器人位姿的2个矩阵; 通过线性回归算法或机器学习算法得到路标信息和机器人位姿,较好解决了传感器数据不同步和数据遗漏问题,其实质是在系统状态空间搜索识别子空间,与其它定位算法相比,不需要线性化模型,具有计算量小、跟踪性能好等优点。
文献[39, 40]将基于矩阵SVD的SLAM与传统的基于概率“位置预测-观测-测量-预测-匹配更新”过程比较,只依靠测距传感器来完成机器人的SLAM问题,从理论上避免了运动模型的偏差和“绑架”问题。
表 1列出了3种方法的优缺点及其改进算法。
| 方法 | 优缺点 | 研究成果 | 改进的思路及性能 |
| EKF-SLAM | 优点: 计算量小(小环境),易于实现; 缺点: 概率密度函数满足高斯分布、线性化处理误差大、对错误数据关联敏感、计算复杂(大环境)。 | 无迹卡尔曼滤波UKF-SLAM[41] 基于容积卡尔曼滤波SLAM[42] 平方根容积卡尔曼滤波SLAM[43] | 通过无迹变换估计后验密度,避免EKF中忽略高阶项带来的问题,无需计算雅克比矩阵,达到3阶精度,精度和稳定性优于EKF-SLAM; 通过相同权重点经过非线性系统方程转换后产生新的点预测系统状态,避免非线性模型的线性化处理。 平方根容积卡尔曼滤波计算后验概率密度,降低线性化误差,稳定性高于EKF-SLAM、UKF-SLAM,定位精度较EKF-SLAM提高1倍。 |
| FastSLAM | 优点: 模型非线性、高维运算降为低维运算,在计算复杂度、数据关联等方面具有优势; 缺点: 样本退化、样本贫化。 | UFastSLAM[44, 45, 46] 辅助UFastSLAM算法[47] CFastSLAM[48, 49] 平方根容积FastSLAM[32] | 无迹变换估计转移概率密度和粒子建议分布函数,具有3阶非线性估计精度,估计精度高于EKF-SLAM、UKF-SLAM、FastSLAM; 建议分布函数引入最近的观测值,估计精度高于UFastSLAM、FastSLAM算法,复杂度高于FastSLAM; 利用容积卡尔曼滤波产生建议分布函数,估计精度高于UFastSLAM、FastSLAM算法,耗时少; 容积律计算非线性转移概率密度,容积律具有3阶非线性估计精度,粒子数目少时,性能优于UFastSLAM与FastSLAM。 |
| SVD-SLAM | 优点: 不需要线性化模型,降维,具有计算量小、跟踪性能好,避免了运动模型的偏差和“绑架”问题; 缺点: 依据实际情况不同,如病态矩阵。 | 协方差矩阵奇异值分解[37, 38] 路标矩阵奇异值分解[40] | 避免了协方差阵的求逆运算、计算误差和舍入误差,保证了状态协方差矩阵失去正定性,减少计算量,提高了算法的稳定性; 把SLAM看做矩阵分解过程,解耦距离矩阵为路标信息矩阵和机器人位姿矩阵,有效抑制噪声对滤波的影响,定位精度高,实时性高。 |
目前,有关移动机器人SLAM研究成果很多,并逐步趋于成熟,使得智能移动机器人的工作环境从办公环境向着未知、非结构化环境方面延伸。结合目前实际应用,未知环境中移动机器人的SLAM问题有待从算法效率、应用领域等方面进一步完善[50]。
1)作为目前移动机器人定位主流的概率算法,需要对系统和观测模型中的噪声做在线自适应评估,对在线实时执行的SLAM算法做深入的研究,实现对移动机器人位姿的有效评估;
2)引入智能化优化算法和多种非线性滤波器相结合的方法,虽然目前已有一些这方面的研究成果,但仍有很大的研究空间;
3)研究粒子滤波中粒子数目与滤波器收敛速度的关系,针对如何克服粒子退化和保持粒子多样性问题,研究自适应重采样策略及提高粒子多样性修复能力的方法,研究考虑了测距传感器精度的粒子建议分布;
4)如何更高效地将测距传感器与其他异质传感器信息进行策略级的高级融合;
5)为使机器人在较短的时间内能够感知的范围尽可能大,进而提高SLAM地图创建的效率,应在探索规划方面展开研究;
6)考虑二维动态环境和三维动态环境下机器人SLAM问题;
7)对于多机协作SLAM技术提高地图创建的准确性和鲁棒性,急需解决自定位多机协作模式、系统控制结构、局部子地图融为全局地图的融合算法及多机分布式多传感器间信息融合等问题。
总体而言,在未来的工作中,将在现有工作基础上,重点需要在信息融合、多机协作系统、室外动态环境的三维实时重建算法等方面开展进一步的研究。
| [1] | WANG Heng, HUANG Shoudong, KHOSOUSSI K, et al. Dimensionality reduction for point feature SLAM problems with spherical covariance matrices[J]. Automatica, 2015, 51:149-157. |
| [2] | VALIENTE D, GIL A, FERNÁNDEZ L, et al. A comparison of EKF and SGD applied to a view-based SLAM approach with omnidirectional images[J]. Robotics and Autonomous Systems, 2014, 62(2):108-229. |
| [3] | STACHNISS C. 机器人地图创建与环境探索[M]. 陈白帆, 刘丽珏, 译, 北京:国防工业出版社, 2013:75. |
| [4] | 程华彬, 张颖超. 基于超声波传感器的移动机器人定位研究[J]. 传感器与微系统, 2013, 32(4):58-60, 64. CHENG Huabin, ZHANG Yingchao. Research on localization of mobile robot based on ultrasonic wave sensor[J]. Transducer and Microsystem Technologies, 2013, 32(4):58-60, 64. |
| [5] | 韩峥, 刘华平,黄文炳,等. 基于Kinect的机械臂目标抓取[J]. 智能系统学报, 2013, 8(2):1-8. HAN Zheng, LIU Huaping, HUANG Wenbing, et al. Kinect-based object grasping by manipulator[J]. CAAI Transactions on Intelligent System, 2013, 8(2):1-8. |
| [6] | HWANG S Y, SONG J B. Monocular vision-based global localization using position and orientation of ceiling features[C] //IEEE International Conference on Robotics and Automation (ICRA).Karlsruhe, Germany, 2013:3770-3775. |
| [7] | WURM K M, STACHNISS C, GRISETTI G. Bridging the gap between feature-and grid-based SLAM[J]. Robotics and Autonomous Systems, 2010, 58(2):140-148. |
| [8] | CHOI H, KIM D Y, HWANG J P, et al. Efficient simultaneous localization and mapping based on ceiling-view:ceiling boundary feature map approach[J]. Advanced Robotics, 2012,26(5-6):653-671. |
| [9] | HWANG S Y, SONG J B, KIM M S. Robust extraction of arbitrary-shaped features in ceiling for upward-looking camera-based SLAM[C] //Proceedings of the 18th IFAC World Congress.Milano, Italy, 2011:8165-8170. |
| [10] | ZHANG S, ADAMS M, TANG F, et al. Geometrical feature extraction using 2D range scanner[C] //The Fourth International Conference on Control and Automation.Montreal, Canada, 2003:901-905. |
| [11] | STURM J, KONOLIGE K, STACHNISS C, et al. Vision-based detection for learning articulation models of cabinet doors and drawers in household environments[C] //IEEE International Conference on Robotics and Automation (ICRA).Anchorage, USA, 2010:362-368. |
| [12] | WU Zhe, KONG Qinjie, LIU Jiapeng, et al. A rectangle detection method for real-time extraction of large panel edge[C] //The 6th International Conference on Image and Graphics (ICIG).Hefei, China, 2011:382-387. |
| [13] | De La PUENTE P, RODRÍGUEZ-L D, VALERO A, et al. 3D feature based mapping towards mobile robots' enhanced performance in rescue missions[C] //IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).St Louis, USA, 2009:1138-1143. |
| [14] | KHAN S, DOMETIOS A, VERGINIS C, et al. RMAP:a rectangular cuboid approximation framework for 3D environment mapping[J]. Autonomous Robots, 2014, 37(3):261-277. |
| [15] | NGUYEN V, MARTINRLLI A, TOMATIS N, et al. A comparison of line extraction algorithms using 2D range data for indoor mobile robotics[J]. Autonomous Robots, 2007, 23(2):97-111. |
| [16] | 满增光, 叶文华, 肖海宁, 等. 从激光扫描数据中提取角点特征的方法[J]. 南京航空航天大学学报, 2012, 44(3):379-383. MAN Zengguang, YE Wenhua, XIAO Haining, et al. Method for corner feature extraction from laser scan data[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(3):379-383. |
| [17] | 徐君, 张国良, 王俊龙. 一种基于激光传感器的自适应直线提取算法[J]. 计算机工程与应用, 2013, 49(2):43-47. XU Jun, ZHANG Guoliang, WANG Junlong. Self-adaption segmentation algorithm for line extraction based on laser sensor[J]. Computer Engineering and Applications, 2013, 49(2):43-47. |
| [18] | 于金霞, 蔡自兴, 段琢华. 基于激光雷达的环境特征提取方法研究[J]. 计算机测量与控制, 2007, 15(11):1550-1552. YU Jinxia, CAI Zixing, DUAN Zhuohua. Research on environmental features extraction with laser scanner[J]. Computer Measurement & Control, 2007, 15(11):1550-1552. |
| [19] | LU Feng, MILIOS E. Globally consistent range scan alignment for environment mapping[J]. Autonomous Robots, 1997, 4(4):333-349. |
| [20] | 王璐, 蔡自兴. 未知环境中移动机器人并发建图与定位(CML)的研究进展[J]. 机器人, 2004, 24(4):380-384.WANG Lu, CAI Zixing. Progress of CML for mobile robots in unknown environments[J]. Robot, 2004, 24(4):380-384. |
| [21] | 强敏利, 张万绪. IEKF滤波在移动机器人定位中的应用[J]. 电子技术应用, 2013, 39(2):74-77. QIANG Minli, ZHANG Wanxu. Application of iterated extended Kalman filtering in mobile robot localization[J]. Application of Electronic Technique, 2013, 39(2):74-77. |
| [22] | 王晓娟, 王宣银. 基于模糊卡尔曼滤波的移动机器人定位研究[J]. 计算机工程与应用, 2011, 47(2):204-206, 216. WANG Xiaojuan, WANG Xuanyin. Research on mobile robot localization based on fuzzy Kalman filtering[J]. Computer Engineering and Applications, 2011, 47(2):204-206, 216. |
| [23] | 邹卫军, 薄煜明. 差分线性化EKF滤波方法研究[J]. 计算机工程与应用, 2009, 45(9):64-66. ZOU Weijun, BO Yuming. Research of EKF based on differential linearization[J]. Computer Engineering and Applications, 2009, 45(9):64-66. |
| [24] | BERGER C. Weak constraints network optimiser[C] //Proceedings of the IEEE International Conference on Robotics and Automation(ICRA).Saint Paul, USA, 2012:1270-1277. |
| [25] | SCHLEICHER D, BERGASA L M, OCAÑA M, et al. Real-time hierarchical stereo Visual SLAM in large-scale environments[J]. Robotics and Autonomous Systems, 2010, 58(8):991-1002. |
| [26] | IDRIS M Y I, AROF H, NOOR N M, et al. A co-processor design to accelerate sequential monocular SLAM EKF process[J]. Measurement, 2012, 45(8):2141-2152. |
| [27] | LEONARD J J, DURRANT-WHYTE H F, COX I J. Dynamic map building for an autonomous mobile robot[J]. The International Journal of Robotics Research, 1992, 11(4):286-298. |
| [28] | LEONARD J J, JACOB H, FEDER S. A computationally efficient method for large-scale concurrent mapping and localization[C] //Proceedings of the Ninth International Symposium on Robotics Research.Snowbird, Utah,USA, 1999:169-176. |
| [29] | PAGAC D, NEBOT E M, DURRANT-WHYTE H. An evidential approach to map-building for autonomous vehicles[J]. IEEE Transactions on Robotics and Automation, 1998, 14(4):623-629. |
| [30] | CADENA C, NEIRA J. SLAM in O(logn) with the combined Kalman-information filter[J]. Robotics and Autonomous Systems, 2010, 58(11):1207-1219. |
| [31] | MURPHY K P. Bayesian map learning in dynamic environments[C] //Proceedings of the Conference on Neural Information Processing System (NIPS).Denver, USA, 1999:1015-1021. |
| [32] | 宋宇, 李庆玲, 康轶非, 等. 平方根容积Rao-Blackwillised粒子滤波SLAM算法[J]. 自动化学报, 2014, 40(2):357-367. SONG Yu, LI Qingling, KANG Yifei, et al. SLAM with square-root cubature Rao-Blackwillised particle filter[J]. Acta Automatica Sinica, 2014, 40(2):357-367. |
| [33] | MONTEMERLO M, THRUN S. Simultaneous localization and mapping with unknown data association using FastSLAM[C] //IEEE International Conference on Robotics and Automation.Taipei, China, 2003:1985-1991. |
| [34] | 康轶非, 宋永端, 宋宇, 等. 不依赖里程计的机器人定位与地图构建[J]. 浙江大学学报:工学版, 2014, 48(3):414-422.KANG Yifei, SONG Yongduan, SONG Yu, et al. Simultaneous localization and mapping without relying on odometer[J]. Journal of Zhejiang University:Engineering Science, 2014, 48(3):414-422. |
| [35] | LIU J S. Metropolized independent sampling with comparisons to rejection sampling and importance sampling[J]. Statistics and Computing, 1996, 6(2):113-119. |
| [36] | 王宏健, 王晶, 刘振业. 基于迭代扩展Kalman滤波建议分布和线性优化重采样的快速同步定位与构图[J]. 电子与信息学报, 2014, 36(2):318-324. WANG Hongjian, WANG Jing, LIU Zhenye. Fast simultaneous localization and mapping based on iterative extended Kalman filter proposal distribution and linear optimization resampling[J]. Journal of Electronics & Information Technology, 2014, 36(2):318-324. |
| [37] | 张友民, 焦凌云, 陈洪亮, 等. 基于奇异值分解的固定区间平滑新方法[J]. 控制理论与应用, 1997, 14(4):579-583. ZHANG Youmin, JIAO Lingyun, CHEN Hongliang, et al. A new fixed-interval smoothing algorithm based on singular value decomposition[J]. Control Theory & Applications, 1997, 14(4):579-583. |
| [38] | 曲从善, 许化龙, 谭营. 一种基于奇异值分解的非线性滤波新算法[J]. 系统仿真学报, 2009, 21(9):2650-2653. QU Congshan, XU Hualong, TAN Ying. New nonlinear filtering algorithm based on SVD[J]. Journal of System Simulation, 2009, 21(9):2650-2653. |
| [39] | 丁帅华, 陈雄, 韩建达. 基于局部子图匹配的SLAM方法[J]. 机器人, 2009, 31(4):296-303. DING Shuaihua, CHEN Xiong, HAN Jianda. A new solution to SLAM problem based on local map matching[J]. Robot, 2009, 31(4):296-303. |
| [40] | BOOTS B, GORDON G J. A spectral learning approach to range-only SLAM[C] //Proceedings of the 30th International Conference on Machine Learning(ICML).Atlanta, Georgia, USA, 2013:19-26. |
| [41] | VAN DER MERWE R, WAN E A. The square-root unscented Kalman filter for state and parameter-estimation[C] //2001 IEEE International Conference on Acoustics, Speech and Signal Processing.Salt Lake,USA, 2001:3461-3464. |
| [42] | BHARANI CHANDRA K P, GU D W, POSTLETHWAITE I. Cubature Kalman filter based localization and mapping[C] //18th IFAC World Congress.Milano, Italy, 2011:2121-2125. |
| [43] | 康轶非, 宋永端, 宋宇, 等. 平方根容积卡尔曼滤波在移动机器人SLAM中的应用[J]. 机器人, 2013, 35(2):186-193. KANG Yifei, SONG Yongduan, SONG Yu, et al. Square-root cubature Kalman filter and its application to SLAM of an mobile robot[J]. Robot, 2013, 35(2):186-193. |
| [44] | KIM C, SAKTHIVEL R, CHUNG W K. Unscented Fast-SLAM:a robust and efficient solution to the SLAM problem[J]. IEEE Transactions on Robotics, 2008, 24(4):808-820. |
| [45] | KIM C, KIM H K, CHUNG W K. Exactly Rao-Blackwellized unscented particle filters for SLAM[C] //2011 IEEE International Conference on Robotics and Automation.Shanghai, China, 2011:3589-3594. |
| [46] | KURT-YAVUZ Z, YAVUZ S. A comparison of EKF, UKF, FastSLAM2.0, and UKF-based FastSLAM algorithms[C] //The 16th International Conference on Intelligent Engineering Systems.Lisbon, Portugal, 2012:37-43. |
| [47] | 张国良, 汤文俊, 敬斌, 等. 辅助粒子滤波算法改进的UFastSLAM算法[J]. 哈尔滨工业大学学报, 2012, 44(11):123-128. ZHANG Guoliang, TANG Wenjun, JING Bin, et al. Improved UFastSLAM algorithm based on auxiliary particle filter[J]. Journal of Harbin Institute of Technology, 2012, 44(11):123-128. |
| [48] | SONG Y, LI Q L, KANG Y F, et al. CFastSLAM:a new Jacobian free solution to SLAM problem[C]//IEEE International Conference on Robotics and Automation (ICRA). Saint Paul, USA, 2012:3063-3068. |
| [49] | 穆静, 蔡远利, 张俊敏. 容积粒子滤波算法及其应用[J]. 西安交通大学学报, 2011, 45(8):13-17. MU Jing, CAI Yuanli, ZHANG Junmin. Cubature particle filter and its application[J]. Journal of Xi'an Jiaotong University, 2011, 45(8):13-17. |
| [50] | 于金霞, 王璐, 蔡自兴. 未知环境中移动机器人自定位技术[M]. 北京:电子工业出版社, 2011. |



