2. 河南大学 管理科学与工程研究所, 河南 开封 475004
2. Research Institute of Management Science and Engineering, He'nan University, Kaifeng 475004, China
布谷鸟搜索算法是由剑桥大学学者Yang和拉曼工程大学Deb于2009年基于对布谷鸟寻窝寄生幼卵行为的模拟,提出的一种新的全局优化算法,即Cuckoo Search(CS)算法[1]。由于其具有控制参数少、寻优能力强和简单易实施等特点,现已成功应用于解决函数优化问题[2]、工程结构优化问题[3]、TSP问题[4]和PID控制器调整[5]等多个领域。此外,通过改进算法参数提高算法性能也成为一个重要的研究领域。Walton对布谷鸟搜索算法的步长进行改进,增加了个体间的信息交流[6]。Zheng在鸟窝位置选择更新方式中加入了高斯扰动项,进而提出基于高斯扰动的布谷鸟搜索算法[7]。苏芙华等通过引入动态局部搜索技术,进一步提高了布谷鸟搜索算法的性能[8]。针对算法在求解复杂函数时,后期收敛精度不高、迭代次数多、运算时间长等问题,本文提出一种基于函数优化的具有动态惯性权重的布谷鸟(cuckoo search with dynamic inertia weight,简称WCS)算法,通过加入动态惯性权重对鸟窝位置进行更新,有效平衡局部搜索和全局搜索之间的关系。实验结果表明,WCS算法能够有效提高算法的收敛精度,减少算法的运行时间,具有较好的优化性能。
1 基本布谷鸟算法布谷鸟算法源于对布谷鸟繁育行为的模拟,是新型有效的全局优化算法。其原理是将布谷鸟所选宿主的鸟窝映射为空间中的解,用宿主鸟巢所在位置的优劣表示解的适应度值,布谷鸟搜索和选择鸟窝的过程就是算法的搜索和优化过程[9]。
布谷鸟算法基于3个理想规则[1]:
规则1 每只布谷鸟每次产一个卵,并随机选择鸟巢孵化它;
规则2 在随机选择的一组鸟巢中,最好的鸟巢被保留至下一代;
规则3 可选择的寄生巢的数量是固定的,寄生巢主人发现外来鸟蛋的概率为Pa,其中0≤Pa≤1。
基于这3个理想规则,Yang等[1]采用式(1)对下一代鸟巢位置X(t+1)进行更新:

基本布谷鸟搜索算法,按照更新式(1)对下一代的鸟窝位置进行更新,并且计算目标函数的适应度值,如果优于上一代适应度值,则保留到下一代,否则保持原来位置不变。随机产生的数值r服从0到1均匀分布,并将其与鸟巢主人发现外来鸟蛋的概率Pa相比较,若r>Pa,则重新产生一组初始解向量,否则保持不变。
2 具有动态惯性权重的布谷鸟搜索算法 2.1 动态惯性权重的选择动态惯性改进策略是一种控制种群探索能力和开发能力的机制,能够有效提高算法的搜索能力,平衡局部搜索和全局搜索之间的关系。Shi和Eberhart[12]将惯性权重引入粒子群算法,作为一种取代速度钳制操作的控制机制,通过惯性权重的调整来控制算法的局部和全局寻优能力。
动态变化惯性权重主要有以下几类:
线性递减 w的取值从较大值线性递减到一个较小的值[13]:
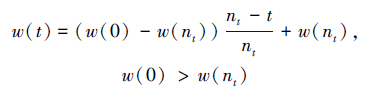
非线性递减 w从较大值非线性递减到一个较小值[14]:

模糊调整 由Eberhart和Shi(1998)采用模糊系统提出的具有动态调整特征的自适应惯性权重[15],但其参数较多,增加了算法的复杂度和实现难度。
随机调整 Eberhart等[16]提出一种动态惯性权重的方法,每次迭代都随机选取高斯分布中的一个惯性权重值,较大的惯性权重和较小的惯性权重随机出现。较大的惯性权重可以避免算法在初期陷入局部最优,同时较小的惯性权重可以解决后期收敛精度不高等问题[17]。
基于以上分析,本文选取动态惯性权重中的随机调整惯性权重对布谷鸟算法进行改进。随机调整的惯性权重服从高斯分布即:w~N(θ,σ)。较大的惯性权重和较小的惯性权重都会随机出现,使得算法能够实现局部搜索和全局搜索的平衡。随机惯性策略w的更新公式为
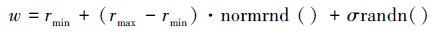
因此,具有动态惯性权重的布谷鸟搜索算法采用动态惯性权重中的随机调整的惯性权重改进鸟窝位置更新方式,WCS算法实现流程如下:
1)确定目标函数f(X),设置优化函数的定义域[-L,L],维度d,发现概率Pa和种群数量n。初始化种群,随机并产生d维向量,即X=(x1,x2,…,xd)T,n个鸟窝的初始位置为:Xi(i=1,2,…,n);
2)计算每个鸟窝的目标函数值,并记录当前鸟窝位置的最优解;
3)保留上代最优鸟窝位置,产生随机动态惯性权重w~N(θ,σ),采用加入动态惯性权重策略的位置更新公式(2)对一代鸟窝位置进行更新;

4)将现有鸟窝位置与上一代鸟窝位置进行比较,若现在位置较好,则将其作为当前的最优位置,否则最优位置不变;
5)用一个随机数r,作为鸟窝主人发现外来鸟蛋的可能性,与发现概率Pa进行比较,若r≤ Pa,则记录当前最优值;若r>Pa,则返回2),随机改变鸟窝位置,得到一组新的鸟窝位置;
6)输出全局最优值。
2.2 动态惯性权重的变化范围对优化效果的影响本文参考文献[18]对动态惯性权重范围的划分进行取值,使用表 2中函数f1和函数f2观察不同惯性权重的变化范围对优化效果的影响。参数设置:种群大小为25,每次运行最大迭代次数为50,对每个函数优化50次。实验结果如表 1所示。表中,1表示惯性权重范围0~0.2,2表示0.2~0.9,3表示0.9~1.2。实验结果表明,当取值在0.9~1.2时,算法找到最优结果的次数较少;当取值在0.2~0.9之间时,算法能够找到最优结果,但是找到最优解的概率不稳定;当取值在0~0.2时,算法能够找到最优结果,准确率较高。因此,随机调整的惯性权重服从高斯分布,且θ取值为0~0.2,σ取值足够小以确保w不会显著大于1。
| f | 惯性权重范围 | 1 | 2 | 3 |
| f1 | 平均迭代次数 | 2.4 | 3.4 | 14.9 |
| 准确率 | 1 | 1 | 2% | |
| f2 | 平均迭代次数 | 2.6 | 8.5 | 2.9 |
| 准确率 | 1 | 6% | 0 |
| 函数 |
平均 时间/s |
平均迭 代次数 |
进化 代数 | 准确率/% | |
| f1 | CS | 9.996 4 | 11.233 3 | 2 500 | 83.33 |
| WCS | 0.170 2 | 4.733 33 | 50 | 100.00 | |
| f2 | CS | 1.021 6 | 4.966 67 | 300 | 13.33 |
| WCS | 0.093 5 | 3.666 67 | 20 | 90.00 | |
| f3 | CS | 2.218 9 | 12.766 7 | 600 | 30.00 |
| WCS | 0.315 4 | 7.9 | 70 | 83.33 | |
| f4 | CS | 3.951 5 | 19.966 7 | 1 100 | 33.33 |
| WCS | 0.848 6 | 9.433 33 | 200 | 93.33 | |
| f5 | CS | 0.045 2 | 4.466 7 | 50 | 100 |
| WCS | 0.043 3 | 5.966 67 | 40 | 100 |
算法的时间复杂性可以从侧面反映算法收敛速度的快慢,如果一个算法收敛,但需要无穷的迭代时间,那么这个算法不具有有效性。基本布谷鸟算法输入的种群规模为N,求解目标函数为f(x),最大迭代次数为n,根据基本布谷鸟算法的流程,假设产生均匀分布随机数的时间为ξ1,下一代鸟窝位置由上代鸟窝位置和Levy飞行机制得到,计算目标函数的时间复杂度为O(N(ξ1n+ f(n)))= O(n+f(n)),更新式(1)产生一组新解的时间为ξ2,新的位置与上代位置进行比较的执行时间为ξ3,若新位置较好,替换上代位置的执行时间为ξ4,在第1个新解产生阶段,时间复杂度为O(N(ξ2n+f(n)+ξ3+ξ4n) )=O(n+ f(n))。在第2个新解阶段,生成新解的执行时间为ξ5,时间复杂度为O(N(ξ5n+f(n)+ξ3+ξ4n)=O(n+f(n))。记录最优鸟巢位置的时间复杂度为O(N(ξ3+ξ4n) =O(n),则对于每一代找到最优解的总的时间复杂度为T(n)=3O(n+f(n))+O(n)=O(n+ f (n))[19]。
同理,分析改进布谷鸟算法的流程,位置更新公式中加入动态惯性权重,设产生动态惯性权重w的执行时间为ξ,种群数量、目标函数和最大迭代次数不变。在第1个新解阶段,时间复杂度为O(N(ξ1n+ξ2n+f(n)+ξ3+ξ4n))=O(n+ f(n)),第2个新解阶段,时间复杂度为O(N(ξ1n+ξ5n+f(n)+ξ3+ξ4n))= O(n+f(n))。因此,更新下一代鸟窝位置的最终时间复杂度不变,仍为T(n)=O(n+f(n)),与基本布谷鸟算法一致,改进后的算法没有增加时间复杂度。
3 WCS算法的收敛性分析标准布谷鸟算法是一种随机算法,文献[20]通过建立Markov链模型,利用随机算法收敛的条件证明了标准CS算法的收敛性,为CS算法全局收敛提供了理论依据。
文献[21]和[22]利用差分方程分别对蝙蝠算法和粒子群算法的收敛性进行了深入分析,本文采取同样的方法,通过建立差分方程对改进的布谷鸟算法进行收敛性分析。改进布谷鸟算法采用式(2)进行下一代鸟窝位置更新,式(2)表示第i个鸟巢在t+1时刻的位置,α为步长控制量,Levy(λ)是随机搜索步长,即
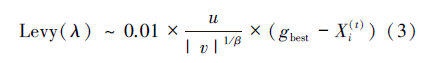


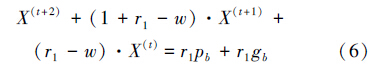
λ2+(1+w-r1)λ+w-r1=0
求解特征方程,得到△=(1+w-r1)2-4(w-r1),因为△=(w-r1-1)2≥0,所以只需要考虑以下2种情况:(a)当△=(w-r1-1)2=0时,即w-r1-1=0。λ1和λ2为特征方程的2个根,若λ1和λ2为实数,‖λ1‖、‖λ2‖分别表示λ1和λ2的绝对值,若为复数,则表示λ1和λ2的模值。
由△=0得:λ1=λ2=-1。此时X(t)=(A0+A1t)λt,A0、A1为待定系数,计算可得:
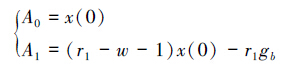
(b)当△>0时,此时X(t)=A0+A1λ1t+ A2λ2t,A0、A1和A2为待定系数,计算得到:

当t→∞时,有极限且趋向于有限值,表示迭代收敛,由此可知,若上面2种情况中X(t)收敛,则需满足条件‖λ1‖<1,‖λ2‖<1[19]。当max(‖λ1‖,‖λ2‖)=1,则有:
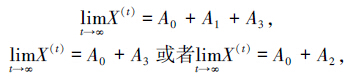
因此,当△=0时,收敛区域为w-r1-1=0;当△>0时,收敛区域需要满足: -1<r1-w<1。综合上面2种情况,收敛区域为-1≤r1-w<1。
4 仿真实验为评估WCS算法的性能,采用5个典型的测试函数进行验证。运行环境:CPU为B940@2.00 GHz,内存2 GB,Matlab R2013a编程环境。其中,函数f1~f5的最优值分别为1、3 600、0、0和-3,测试函数f1~f5的数学表达式和自变量的取值范围如下:
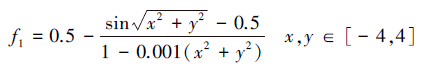

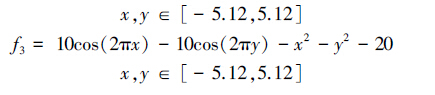
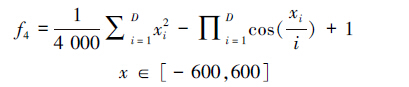
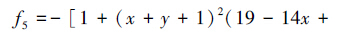
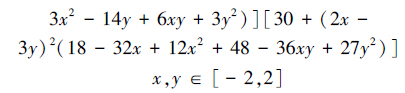
算法参数设置为:种群规模n=25,发现概率Pa=0.25。惯性权重从高斯分布中取值并随机调整。每个函数分别进行30次独立仿真实验,平均时间为算法找到最优解所用时间的平均值,其单位为秒。平均迭代次数为算法收敛到最优解的代数的平均值。进化代数为算法找到最优解的最大迭代次数的最小值。准确率为算法找到最优解的次数与运行总次数的百分比。WCS算法与CS算法比较,如图 1~6所示,仿真运算结果如表 2所示。
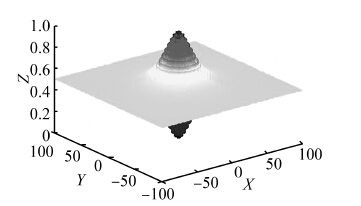 |
| 图 1 f1图像Fig. 1 Image of f1 |
1)Schaffer函数
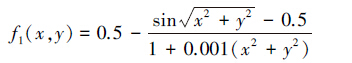
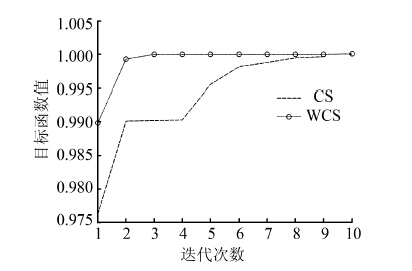 |
| 图 2 f1算法收敛状态对比图Fig. 2 Convergence state of CS and WCS on f1 |
2)Needle-in-haystack函数
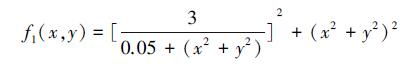
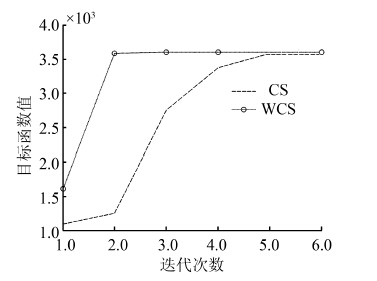 |
| 图 3 f2算法收敛对比图Fig. 3 Convergence state of CS and WCS on f2 |
 |
| 图 4 f3算法收敛对比图Fig. 4 Convergence state of CS and WCS on f3 |
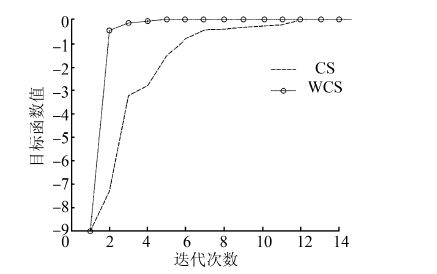 |
| 图 5 f4算法收敛对比图Fig. 5 Convergence state of CS and WCS on f4 |
 |
| 图 6 f5算法收敛对比图Fig. 6 Convergence state of CS and WCS on f5 |
以上函数收敛图表明,改进后的算法和基本算法相比,迭代次数更少,收敛速度更快,收敛精度更高,具有更好的优化性能。
表 2运算结果表明,对于5个测试函数,改进后的算法找到最优解的次数更多,时间更短,相比于基本算法找到最优解的准确率更高。当基本CS算法面对较为复杂的函数优化问题时,如f1,增加迭代次数为2 500,基本算法运行时间是改进后算法的58.7倍,收敛到最优解的迭代次数是改进后算法的2.4倍,准确率只有改进后算法的83%。因此,改进后的算法可以更好地解决函数优化问题。
4.2 WCS算法与其他算法的比较用以上函数对WCS算法与CS算法、粒子群算法(PSO)、蚁群算法(ACO)、引力搜索算法(GSA)和蝙蝠算法(BA)进行性能测试,运算结果如表 3所示。
| f | 算法 | 最优值 | 平均值 | 最差值 | 标准差 |
| f1 | CS | 0.999 974 | 0.997 223 | 0.990 284 | 0.003 559 |
| WCS | 1 | 1 | 1 | 0 | |
| PSO | 1 | -0.999 87 | -0.996 87 | 0.000 619 | |
| ACO | 1 | 1 | 1 | 0 | |
| GSA | 1 | 0.993 167 | 0.990 284 | 0.003 921 | |
| BA | 1 | 0.997 667 | 0.990 280 | 0.004 193 | |
| f2 | CS | 3.60×103 | 3.55×103 | 2.75×103 | 194.710 1 |
| WCS | 3 600 | 3 600 | 3 600 | 0 | |
| PSO | 3.60×103 | 3.60×103 | 3.59×103 | 0.000 162 | |
| ACO | 3 600 | 3 600 | 3 600 | 0 | |
| GSA | 3.58×103 | 3.14×103 | 2.71×103 | 325.587 9 | |
| BA | 3 600 | 3 600 | 3 600 | 0 | |
| f3 | CS | -0.000 890 | -0.202 307 | -1.041 848 | 0.274 363 |
| WCS | 0 | 0 | 0 | 0 | |
| PSO | 0 | -1.69×10-5 | -5.08×10-4 | 0.000 077 | |
| ACO | 0 | 0 | 0 | 0 | |
| GSA | 0 | -0.047 840 | -0.853 809 | 0.127 847 | |
| BA | 0 | -2.82×10-7 | -4.64×10-6 | 6.62×10-7 | |
| f4 | CS | -6.67×10-9 | -2.52×10-4 | -6.28×10-3 | 0.000 989 |
| WCS | 0 | 0 | 0 | 0 | |
| PSO | -2.36×10-13 | 5.43×10-11 | -5.18×10-10 | 7.99×10-11 | |
| ACO | 0 | 0 | 0 | 0 | |
| GSA | 0 | -0.006 084 | -0.029 799 | 0.006 14 | |
| BA | -3.58×10-12 | -3.99×10-10 | -1.41×10-9 | 3.98×10-10 | |
| f5 | CS | -3 | -3 | -3 | 0 |
| WCS | -3 | -3 | -3 | 0 | |
| PSO | -3.000 000 1 | -3.000 004 | -3.000 019 | 4.98×10-8 | |
| ACO | -3 | -3.167 406 | -3.665 694 | 0.176 342 | |
| GSA | -3 | -3.010 484 | -3.391 7 | 0.058 115 | |
| BA | -3 | -3 | -3 | 0 |
其中,为了更加公平地测试算法性能,每个算法独立运行50次,种群数量都为50,迭代次数1 000。CS算法和WCS算法参数设置为:发现概率Pa=0.25。PSO参数设置为w=0.729,c1=c2=1.494 45[23] 。蚁群算法参数设置为:α=β=1,r=0.5,ρ=0.7,Q=1[24]。引力搜索算法参数设置为:T=1 000,G0=100,α=50。蝙蝠算法参数设置为:Ai=0.25,ri=0.5,α=r=0.9[25]。
实验结果表明,对于函数f1~f5,相比于其他算法,WCS算法能够很快找到最优解。蚁群算法表现次之,对于f1~f4可以收敛到最优解,但对f5求解精度不够。CS算法求解的稳定性不高。对于函数f1和f2,WCS算法和蚁群算法都有很好的收敛性,能快速找到最优解;对于函数f3,WCS算法和蚁群算法性能明显优于其他算法;对于函数f4,WCS算法和蚁群算法能够收敛到最优解;对于函数f5,CS算法、WCS算法和新型蝙蝠算法优化性能明显优于其他算法。
4.3 种群大小对惯性权重选择的影响算法参数的选择可能对算法性能产生重要影响,本文重点讨论种群大小对算法性能的影响。种群规模由25增加至100,最大迭代次数为300,其他参数设置不变,每个函数独立运行50次,1、2和3分别表示惯性权重的取值范围0~0.2、0.2~0.9和0.9~1.2,4表示基本布谷鸟算法。在n为25和100两种情况下,函数f1~f3找到最优解的达优率如表 4所示。
| f | n | 1 | 2 | 3 | 4 |
| f1 | 25 | 1 | 0.9 | 0 | 0 |
| 100 | 1 | 1 | 0 | 0 | |
| f2 | 25 | 1 | 1 | 0.04 | 0.12 |
| 100 | 1 | 1 | 0.08 | 0.08 | |
| f3 | 25 | 1 | 1 | 0 | 0 |
| 100 | 1 | 1 | 0 | 0 |
由表 4可得,种群规模增大后,CS算法优化性能基本不变,函数2在种群规模增大后的达优率甚至出现减少的情况;惯性权重范围在0.2~0.9和0.9~1.2两个区间的算法优化性能并没有得到明显改善,最佳惯性权重范围仍然是0~0.2,说明种群规模的改变,对算法收敛效果的影响不显著。
5 结束语针对布谷鸟算法在求解函数最优化问题中存在的收敛度不高、收敛速度慢等问题,本文提出了一种改进方法:通过引入动态惯性权重改进鸟窝位置的更新方式,对动态惯性权重的取值范围进行分析,找到求解最优的惯性权重取值范围。并利用差分方程对改进算法进行了收敛性分析。研究发现改进后的算法通过动态惯性权重控制种群探索能力和开发能力,能够有效平衡局部搜索能力和全局搜索能力之间的关系。仿真实验结果表明,与基本布谷鸟算法相比,WCS算法可以显著减少迭代次数,缩短运行时间;与其他算法相比,WCS算法也有较强的收敛性和鲁棒性。最后,对算法参数进行了讨论,当种群规模增大后,仍需惯性权重的调节,且惯性权重的选择范围不变,进一步说明,加入动态惯性权重后的算法具有更好的优化性能。
| [1] | YANG Xinshe, DEB S. Cuckoo search via Lévy flights[C]//World Congress on Nature & Biologically Inspired Computing. Coimbatore, India, 2009: 210-214. |
| [2] | 李煜, 马良. 新型元启发式布谷鸟搜索算法[J]. 系统工程, 2012, 30(8): 64-69. LI Yu, MA Liang. A new metaheuristic cuckoo search algorithm[J]. Systems Engineering, 2012, 30(8): 64-69. |
| [3] | 陈乐, 龙文. 求解工程结构优化问题的改进布谷鸟搜索算法[J]. 计算机应用研究, 2014, 31(3): 679-683. CHEN Le, LONG Wen. Modified cuckoo search algorithm for solving engineering structural optimization problem[J]. Application Research of Computers, 2014, 31(3): 679-683. |
| [4] | OUAARAB A, AHIOD B, YANG Xinshe. Discrete cuckoo search algorithm for the travelling salesman problem[J]. Neural Computing and Applications, 2014, 24(7/8): 1659-1669. |
| [5] | SETHI R, PANDA S, SAHOO B P. Cuckoo search algorithm based optimal tuning of PID structured TCSC controller[M]//JAIN L C, BEHERA H S, MANDAL J K, et al. Computational Intelligence in Data Mining-Volume 1. Odisha: Springer, 2015: 251-263. |
| [6] | WALTON S, HASSAN O, MORGAN K, et al. Modified cuckoo search: a new gradient free optimisation algorithm[J]. Chaos, Solitons and Fractals, 2011, 44(9): 710-718. |
| [7] | ZHENG Hongqing, ZHOU Yongquan. A novel cuckoo search optimization algorithm based on Gauss distribution[J]. Journal of Computational Information Systems, 2012, 8(10): 4193-4200. |
| [8] | 苏芙华, 刘云连, 伍铁斌. 求解无约束优化问题的改进布谷鸟搜索算法[J]. 计算机工程, 2014, 40(5): 224-227, 233. SU Fuhua, LIU Yunlian, WU Tiebin. Modified cuckoo search algorithm for solving unconstrained optimization problem[J]. Computer Engineering, 2014, 40(5): 224-227, 233. |
| [9] | 龙文, 陈乐. 求解约束化工优化问题的混合布谷鸟搜索算法[J]. 计算机应用, 2014, 34(2): 523-527. LONG Wen, CHEN Le. Hybrid cuckoo search algorithm for solving constrained chemical engineering optimization problems[J]. Journal of Computer Applications, 2014, 34(2): 523-527. |
| [10] | VISWANATHAN G M, AFANASYEV V, BULDYREV S V, et al. Lévy flights in random searches[J]. Physica A:Statistical Mechanics and its Applications, 2000, 282(1/2): 1-12. |
| [11] | 邓鑫洋, 邓勇, 章雅娟, 等. 一种信度马尔科夫模型及应用[J]. 自动化学报, 2012, 38(4): 666-672. DENG Xinyang, DENG Yong, ZHANG Yajuan, et al. A belief Markov model and its application[J]. Acta Automatica Sinica, 2012, 38(4): 666-672. |
| [12] | SHI Yuhui, EBERHART R. A modified particle swarm optimizer[C]//IEEE World Congress on Computational Intelligence, The 1998 IEEE International Conference on Evolutionary Computation Proceedings. Anchorage, USA, 1998: 69-73. |
| [13] | SHI Yuhui, EBERHART R C. Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation. Washington DC, USA, 1999, 3: 1945-1949. |
| [14] | PERAM T, VEERAMACHANENI K, MOHAN C K. Fitness-distance-ratio based particle swarmoptimization[C]//Proceedings of the 2003 IEEE Swarm Intelligence Symposium. Indianapolis, USA, 2003: 174-181. |
| [15] | SHI Yuhui, EBERHART R C. Fuzzy adaptive particle swarm optimization[C]//Proceedings of the 2001 Congress on Evolutionary Computation. Seoul, Korea, 2001: 101-106. |
| [16] | EBERHART R C, SHI Yuhui. Tracking and optimizing dynamic systems with particle swarms[C]//Proceedings of the 2001 Congress on Evolutionary Computation. Seoul, Korea, 2001: 94-100. |
| [17] | ZHANG Liping, YU Huanjun, HU Shangxu. A new approach to improve particle swarm Optimization[C]//Genetic and Evolutionary Computation—GECCO 2003. Berlin Heidelberg, Germany, 2003: 134-139. |
| [18] | 王俊伟, 汪定伟. 粒子群算法中惯性权重的实验与分析[J]. 系统工程学报, 2005, 20(2): 194-198. WANG Junwei, WANG Dingwei. Experiments and analysis on inertia weight in particle swarm optimization[J]. Journal of Systems Engineering, 2005, 20(2): 194-198. |
| [19] | 张永韡, 汪镭, 吴启迪. 动态适应布谷鸟搜索算法[J]. 控制与决策, 2014, 29(4): 617-622. ZHANG Yongwei, WANG Lei, WU Qidi. Dynamic adaptation cuckoo search algorithm[J]. Control and Decision, 2014, 29(4): 617-622. |
| [20] | 王凡, 贺兴时, 王燕, 等. 基于 CS 算法的Markov 模型及收敛性分析[J]. 计算机工程, 2012, 38(11): 180-182, 185. WANG Fan, HE Xingshi, WANG Yan, et al. Markov model and convergence analysis based on cuckoo search algorithm[J]. Computer Engineering, 2012, 38(11): 180-182, 185. |
| [21] | 李枝勇, 马良, 张惠珍. 蝙蝠算法收敛性分析[J]. 数学的实践与认识, 2013, 43(12): 182-190. LI Zhiyong, MA Liang, ZHANG Huizhen. Convergence analysis of bat algorithm[J]. Mathematics in Practice and Theory, 2013, 43(12): 182-190. |
| [22] | 刘洪波, 王秀坤, 谭国真. 粒子群优化算法的收敛性分析及其混沌改进算法[J]. 控制与决策, 2006, 21(6): 636-640. LIU Hongbo, WANG Xiukun, TAN Guozhen. Convergence analysis of particle swarm optimization and its improved algorithm based on chaos[J]. Control and Decision, 2006, 21(6): 636-640. |
| [23] | EBERHART R C, SHI Y. Comparing inertia weights and constriction factors in particle swarm optimization[C]//Proceedings of the 2000 Congress on Evolutionary Computation. La Jolla, Germany, 2000: 84-88. |
| [24] | 马良. 基于蚂蚁算法的函数优化[J]. 控制与决 策, 2002, 17(增刊): 719-722. MA Liang. Ant algorithm based function optimization[J]. Control and Decision, 2002, 17(S): 719-722. |
| [25] | 李枝勇, 马良, 张惠珍. 多目标 0-1 规划问题的蝙蝠算法[J]. 智能系统学报, 2014, 9(6): 672 -676. LI Zhiyong, MA Liang, ZHANG Huizhen. Bat algorithm for the multi-objective 0-1 programming problem[J]. CAAI Transactions on Intelligent Systems, 2014, 9(6): 672-676. |



