2. 江苏大学 计算机科学与通信工程学院, 江苏 镇江 212013
2. School of Computer Science and Communication Engineering, Jiangsu University, Zhenjiang 212013, China
聚类是一项重要的研究工作,已经成为数据挖掘、统计分析以及压缩算法等领域的研究重点。聚类研究领域有大量经典的算法涌现,如K-means,PAM,WaveCluster等。其中K-means算法因其简单、易于实现,获得了广泛的应用。现代数据挖掘技术的一个突出特点是需要处理大规模数据集。经典的K-means算法在处理大规模数据集时,无法一次性把数据集全部装载入内存,需要多次扫描硬盘上的数据,整个聚类过程相当耗时。因其应用的广泛性,很多研究人员选择对其进行优化,使其适应大规模数据集聚类的应用需求。值得注意的是,在过去的几十年中,CPU的主频几乎每两年提高一倍,与此相对应的内存频率却没有相对应的提高。内存与CPU之间处理数据的能力差距越来越大,极大地影响了应用程序的性能。同时,工程师们开始认识到,仅仅提高单核芯片的频率会产生过多热量且无法带来希望的性能改善。于是,CMP(chip multi-processor)成为了先进处理器的发展趋势。CMP可以在大幅提高处理性能的同时降低CPU主频,减少能源消耗。然而仅简单提供CMP环境并不能直接带来应用程序性能的提高,需要研发人员针对CMP环境对有关算法进行优化,才能使得应用程序更好的利用CPU的多核计算能力,提高程序的运行效率[1]。
本文针对提高大规模数据集聚类效率的问题,着重研究单机多核环境下(CMP)K-means算法的并行化改进,提出了一种Multi-core K-means (MC-K-means)算法。该算法对原K-means算法的聚类任务进行了分解,设计了相互独立且均衡的聚类子任务交由各线程并行执行,能够充分利用现代CPU的多核计算能力,提高大规模数据集的聚类效率。
1 研究背景 1.1 确定性聚类的基本概念金属橡胶隔振器在飞机液压管道上的应用如图 1所示,从图 1看出,金属橡胶放置在外围卡箍的凹槽内,传统管道固定一般直接与外围卡箍接触或之间有薄的橡胶垫作为隔振装 。
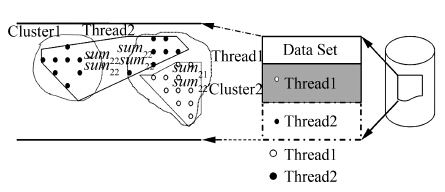 |
| 图 1 MC-K-means算法示意Fig. 1 Illustration of MC-K-means |
定义1 确定性聚类的输入可以用一组有序对(X,s)或(X,d)来表示,这里X表示一组样本,s和d分别是度量样本间相似度或相异度(距离)的标准。确定性聚类系统的输出是一个个分区,例如C={C1,C2,…,Ck},其中Ci(i=1,2…,K)是X 的子集,且满足: C1∪C2∪,… ,∪Ck=X;Ci∩Cj = ∅,i≠j 。
C中的成员C1,C2,…,Ck叫做类或簇(Cluster),每一个类或簇都是通过一些特征描述的,通常有如下几种表示方式:
1) 通过它们的中心或类的边界点表示空间的一类点。
2) 使用聚类树中的结点,图形化地表示一个类。
3) 使用样本属性的逻辑表达式表示类。 1.2 相关的研究工作
为了解决K-means算法对大规模数据集聚类效率较低的问题,有研究者提出了只需要扫描一遍原始数据集即产生聚类结果的算法。这些算法只需读入大规模数据集中的一部分进入主存或者分批读入数据集进行聚类,扫描数据集一遍即完成聚类。相应的算法有random-kmeans,Dynamic incremental K-means[2],Single pass kernel K-means[3],scalable-kmeans[4],等。其中,由Microsoft Research的Redmond等提出的scalable-kmeans算法性能优越,受到了广泛的重视,并被集成到SQL SERVER 2008中。类似研究的主要目的是优化K-means算法,减少数据集的读取次数。有研究者从优化K-means聚类初始条件设置的角度,利用自适应技术、启发式算法以及半监督技术等实现K-means初始聚类中心或者聚类个数的优化选择,加速K-means聚类的收敛过程,提高聚类的效率以及结果的质量[5, 6, 7]。有研究人员从减少大规模数据集数据维度的角度,降低聚类迭代过程的计算量,提高K-means聚类算法的效率[8, 9]。以上相关的研究工作切实提高了K-means聚类的效率,然而这些新算法并没有利用分布式环境提高聚类的效率。最近有研究人员进行了SMP、DMP环境下的集群多处理器K-means聚类的研究工作,提高了大规模数据集的聚类效率[10 ,11]。直接针对共享内存多处理器系统以及分布式内存多处理器环境进行K-means的并行化,需要考虑复杂的数据划分、节点容错等并行化的基本问题且需要消耗大量的节点间同步以及数据网络传输的时间。随着类似Google MapReduce以及Apache的Hadoop的出现和广泛使用,在这些编程模型的基础之上进行分布式开发变得相对容易,分布式的基本问题可以依靠基础编程模型来解决。很多研究人员利用MapReduce的算法模型,针对K-means聚类过程的并行化进行了大量深入的研究工作,取得了很多重要的研究成果,使得K-means算法可用于大规模数据集聚类的应用场合。然而这些算法更多考虑的是多处理器分布式场景下的K-means并行化,较少考虑到单机CPU的多核利用。除此之外,并不是所有的聚类算法都适合以MapReduce的形式进行并行化的,且为了适应MapReduce的编程架构,有时反而会增加额外的计算量与通信量[12, 13, 14]。
现代CPU技术的发展,使得单机的运行环境也发生了极大的变化。多核处理器的出现提高了CPU的计算性能,降低了CPU的功耗。尽管如此,传统的算法并不能直接从多核CPU中获益,需要针对多核CPU的特点进行并行化改进与优化,才能充分利用多核CPU的计算能力。因此,研究单机CMP环境下K-means算法的并行化方法对提高单机K-means算法的聚类效率具有重要的现实意义,并且与DMP、SMP环境下的K-means聚类过程可以有效的结合,作为DMP、SMP环境下K-means聚类算法的有效补充。也有研究人员开始着手研究CMP环境下K-menas算法的并行化,但是相关研究尚处于起步阶段,算法实现仍存在进一步改进的空间[15, 16]。
1.3 多核处理器的出现2005年,当主频接近4 GHz时,CPU的主要制造厂商英特尔和AMD公司发现单纯的主频提升已经无法明显提升系统整体性能。由于CPU片内流水线过长,使得单位频率效能低下,加上由于缓存的增加和对漏电流控制的不利,造成CPU功耗大幅度增加。随着功耗的增大,散热问题也越来越成为一个无法逾越的障碍。于是,出现了多核心CPU的解决方案。
其实较早以前已经有研究人员提出了利用单芯片多核心处理器(CMP)技术来代替复杂度越来越高的单核心CPU。IBM、IP、SUN等企业也在服务器领域投入了一定的多核CPU进行商用。然而由于当时的服务器多核CPU价格过于昂贵、应用面窄、并没有真正发展起来。
2006年,多核CPU进入了迅猛的发展时期,Intel的Core,Xeon以及AMD的Athlon,Barcelona等受到了广泛的欢迎。这些CPU在性能得到极大提升的同时,功耗反而得到了降低。
值得注意的是OS并不能自动的让某个应用程序直接利用CPU的多核,而是需要进行有关算法的CMP并行化改进。对于数据挖掘中的聚类、关联规则挖掘等计算密集型、I/O密集型应用而言,对原有算法进行并行化改进,提高算法的执行效率,尽快给出挖掘结果成为了当务之急。研究具有较强的现实意义[1]。
2 K-means算法详细描述K-means算法,也被称为K-平均或K-均值算法,是目前得到广泛应用的一种聚类算法[17]。其相似度的计算根据一个簇中对象的平均值来进行。K-means 算法以k为参数,把n 个数据点分为k 个簇,使得簇内具有较高的相似度,而簇间的相似度较低。
算法首先随机地选择k个对象,每个对象初始地代表了一个簇的平均值或中心。对剩余的每个对象根据其与各个簇中心的距离,将它赋予最近的簇,然后重新计算每个簇的平均值。这个过程不断重复,直到准则函数收敛。准则函数定义为: E=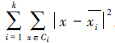 。这里的准则函数E是数据集中所有数据点的平方误差总和,x是数据集空间中的点,
。这里的准则函数E是数据集中所有数据点的平方误差总和,x是数据集空间中的点,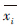 是簇Ci的平均值。准则函数E使得生成的结果簇尽可能的紧凑和独立。
是簇Ci的平均值。准则函数E使得生成的结果簇尽可能的紧凑和独立。
算法1 K-means (Dataset D,ClusterNumber K)
输入:事务数据库D,聚类簇的数量K
输出:K个聚类,使得平方误差准则E最小
1) assign initial value for means;
//任意选择k个对象作为初始的簇中心
2) REPEAT;
3)FOR j =1 to n DO assign each xj to the closest clusters mean;
//根据簇中对象的平均值将每个对象分配给最近的簇
4) ;
;
//更新簇的平均值,即计算每个簇中对象的平均值
5) ;
;
//计算准则函数E
6) Until Enew-Elast<ε ,ε 为预先设定的一个较小的值;
//表示E不再产生明显的变化
K-means是解决聚类问题的一种经典算法,该算法实现起来较为简单且有非常好的可扩展性。因此,很多科研人员在研究针对大规模数据集的高效聚类算法时,往往会以K-means算法作为首选进行改进和优化。
分析K-means 算法的时间复杂度,其运行时间主要消耗在:1)数据集读取所产生的I/O;2)判断每一个数据点(数据记录)的所属类别;3)计算每一个类别(簇)的中心;4)计算准则函数E。而这4个阶段均可以很好地并行化,以此利用现代CPU的多核特性,最大化的发挥CPU的性能,提高聚类效率。
为此,本文提出了一种Multi-core K-means算法(MC-K-means),该算法对上述4个过程分别进行并行化,充分利用CPU的多核特性,进一步提高K-means算法的聚类效率。新算法可作为SMP、DMP分布式环境下聚类算法以及增量OneScan聚类算法的有效补充,提高单节点的聚类效率,从而提高整体的聚类效率。
3 CMP上基于数据集划分的大规模数据集K-means多核优化算法3.1 MC-K-means算法详细描述
在CMP环境下对K-means聚类算法进行改进以适应大规模数据集,关键是要改进原有算法的串行执行部分为并行执行。分析K-means算法可以发现,在较为消耗资源的数据集读取阶段、数据点所属类别判断阶段、每个新簇的簇中心计算阶段以及准则函数的计算阶段,这些阶段均可进行并行化改进,且由于其所需计算的性质,都可以较好的做到多核之间的负载均衡。
改进后的MC-K-means算法详细描述如下。其中关键步骤如图 1所示,为了方便描述,图中以2线程为例进行说明,可推广到n线程的情形。
算法2 MC-K-means (Dataset D,ClusterNumber K)
输入:事务数据库D,聚类的簇的数量K
输出:K个聚类,使得平方误差准则E最小
1) random assign initial value for means;
//任意选择k个对象作为初始的簇中心
2)thread_count=Runtime.getRunTime().availabkleProcessors/(1-blockCoefficient);0<=blockCoefficient<1;
//计算线程数
3)executeService service=Excute.newFixedThreadPool(thread_count);
// 创建线程池
4) divide the data set into n parts equally and create n tasks to read every data set,where n = thread_count;
//装载数据
5)thread_count=Runtime.getRunTime().availabkleProcessors;
6)threadPool=Excute.newFixedThreadPool(thread_count);
//创建线程池,计算准则函数E
7) divide the data set into
parts equally and create
tasks to compute the category,where
= thread_count;
8) repeat
9) for every data_setj
10) let one task j to assign each data point of the data_set j to the closest clusters center and record the category;
11)until every data_setj is finished;
12)for every equally data_setj//计算每个簇的簇中心;
13)let one task j to compute the sumijand numij of data_set j partly,j=1,2,…n,i=1,2,…k ;
14)until every equally data_set j is finished;
15)join the results of every task j to get total_sum i= ,i =1,2,…,k;
,i =1,2,…,k;
16)cluster_center i = total_sum i/ total_num i,i=1,2,…,k;
//每个线程均可访问中心值,以便再次划分数据
17)for every equally data_set j //计算每个簇部分准则函数
18)let one task j to compute the Eij of data_set j partly,j=1,2,…,n,i=1,2,…,k;
19)until every equally data_set j is finished;
20)join the results of every task j to get total_Ei=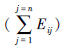 ,i =1,2,…,k;
,i =1,2,…,k;
21) 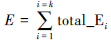 ;
;
22)until E new -E last <ε ,ε is a preset very small threshold
在读入外存数据时,考虑到数据源可能存在于网络数据库中,在读取时会有一定的延时,多开线程可有效利用CPU的多核,因此考虑设置Runtime.getRunTime().availabkleProcessors/(1-blockCoefficient)大小的线程池,其中blockCoefficient=数据记录I/O阻塞时间/数据记录处理时间,在运行时可根据数据源的延时动态调整。
在装载数据之后,判断每一数据点的所属类别时采用的是欧几里得距离的平方 d(x,y)2=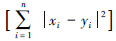 。该计算对于每个数据点的计算量均是相同的,等分数据即可做到负载平衡。除此之外,该过程是计算密集型的,多开线程对提高效率无益,反而会因为CPU频繁的线程切换而降低运行效率。因此开设线程个数与CPU核心数availabkleProcessors相同的线程池;又因为距离计算任务的计算量对每个数据点是一样的,所以MC-K-means算法等分数据,创建availabkleProcessors个任务进行数据点类别判断的计算,并交由线程池调度执行。
。该计算对于每个数据点的计算量均是相同的,等分数据即可做到负载平衡。除此之外,该过程是计算密集型的,多开线程对提高效率无益,反而会因为CPU频繁的线程切换而降低运行效率。因此开设线程个数与CPU核心数availabkleProcessors相同的线程池;又因为距离计算任务的计算量对每个数据点是一样的,所以MC-K-means算法等分数据,创建availabkleProcessors个任务进行数据点类别判断的计算,并交由线程池调度执行。
计算每一个聚类簇的簇中心,仍然是一个计算密集型的任务,因此在此阶段开设线程数与CPU核心数相同的线程池。MC-K-means算法针对之前等分的数据集,每个线程j计算被分配的数据集归属于每个分类i的 sum ij 以及 num ij ,并汇总j个线程的结果得到total_sumij 以及 total_numij ,最终得到 cluster_center i 。采用针对等分数据集的方法使得簇中心计算的各任务相对均衡。在准则函数E的计算过程中也采用了同样的负载均衡的方法。
CMP系统是共享内存的,上述MC-K-means算法仅在访问共享变量及每部分数据处理完毕时需要进行同步,避免了数据集通过网络在节点之间传输造成的时间消耗,算法具有较高的执行效率。
4 实验结果以及分析为了验证算法的有效性,依据前述MC-K-means算法的主要思想,使用Java语言实现了MC-K-means以及K-means算法[18, 19]。实验平台为HP PRO 3380 MT,Window XP_SP3,4 GB内存,jdk7u51以及HP ProLiant DL388p Gen8,RedHat 9.0,32 GB内存,jdk7u51。因为是做CPU多核加速的有关实验,所以需要针对不同实验平台中不同类型的CPU进行测试。HP PRO 3380 MT平台采用的CPU是Intel i3-3240@3.40 GHz,核心类型为Ivy Bridge,64位CPU,双核,四线程,支持超线程技术,3 MB三级缓存,双通道。HP ProLiant DL388p Gen8平台采用的CPU是Intel Xeon E5-2609@2.40 GHz,核心类型为Sandy Bridge,64位CPU,四核,四线程,10 MB三级缓存,四通道。
对比算法为文献[15]描述的基于MapReduce的并行K-means算法(PKMeans_MR)以及文献[16]描述的PKMeans_MT算法。在实验中根据上述文献描述的算法思想分别实现了各算法进行对比实验。因为相同初始化条件下各算法最终聚类的结果是一样的,所以实验主要对比分析相关算法的执行时间以及加速率情况。
4.1 人工生成数据集测试人工生成数据集由数据生成程序根据K个高斯分布随机产生,每个高斯分布设置一个随机权重来确定是否产生数据。每一个高斯分布的中心是随机产生的,区间为[-5,5]。数据点每个维度值的产生区间为[0.7,1.5]。产生的人工数据集包含100维,180 000个数据点,数据集使用二进制bin文件保存。本次实验因为数据集以及聚类测试算法是在同一台计算机上的,所以读取数据集时的阻塞系数blockCoefficient设置为0。聚类簇数量设置为k=5。
整个实验随机产生5个不同的人工生成数据集,针对每个数据集,分别执行MC-K-means、PKMeans_MR、PKMeans_MT以及K-means算法各10次,各自共运行50次,最后以聚类时间的平均值作为算法聚类效率的评价。实验结果如图 2、3所示。
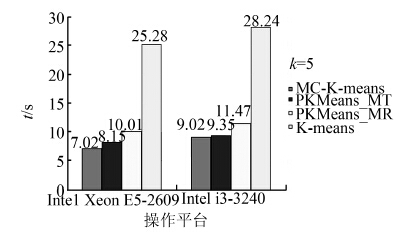 |
| 图 2 运行时间对比Fig. 2 Comparison of run time |
 |
| 图 3 加速率对比Fig. 3 Comparison of speedup rate |
该数据集较为规整,算法运行收敛较快。从实验结果可以看出:针对服务器领域的Xeon E5-2609,虽然主频较低,但依靠较大的L3缓存以及四通道的内存控制器,使得各算法取得了较高的执行效率。K-means算法在该平台环境下执行消耗了25.28 s,PKMeans_MR消耗了10.01 s,PKMeans_MT消耗了8.15 s,MC-K-means则需要7.02 s。而在 i3-3240所在平台环境下,K-means算法消耗了28.24 s,PKMeans_MR消耗了11.47 s,PKMeans_MT消耗了9.35 s,MC-K-means在该平台则需要9.02 s。从并行化改造后各算法的执行结果来看,在Xeon E5-2609所在平台,算法获得了更高的加速比。这主要是由于Xeon E5-2609是四核四线程的,拥有真实的四核心,可以更好地并行完成各并行化算法划分的多任务聚类工作。而i3-3240是双核心的,依靠超线程技术实现的四线程并行,但是CPU的双物理核心需要频繁的进行线程上下文的切换,消耗了一部分的运行时间,获得了较低的加速比。
其中,MC-Kmeans算法在读取数据集、判断每个数据点的所属类别、计算簇中心以及计算准则函数E这4个阶段均进行了并行化改进。且在这4个阶段中,每个数据点的任务量是相当的,因此MC-K-means算法所采取的等分数据集的方法可以取得较好的负载均衡性,算法取得了对比算法中最高的加速率。
PKMeans_MT算法取得了较低的加速率。分析算法可知,该算法仅在读取数据集以及迭代计算每个数据点的归属时利用parfor函数进行了并行化。对新分类中心点的计算及准则函数的计算均没有并行化,且算法需要依托MATLAB平台,故取得了较低的加速率。
PKMeans_MR算法在对比算法中取得了最低的加速率。分析算法可知,PKMeans_MR算法改进原K-means算法,使其以MapReduce方式运行,节点之间在迭代时需要多次通信、多次同步,且算法需适应MapReduce固有模式,降低了算法的运行效率,因此取得了最低的加速率。但对比原K-means算法仍提高了一倍多的运行效率。
可以看出,对K-means进行并行化改进,适应了多核CPU的发展趋势,可以极大程度提高算法的运行效率,满足处理大规模数据集的需要。
逐步增大生成数据集的规模,生成的人工数据集为100维,分别包含180 000个数据点,360 000个数据点,540 000个数据点,720 000个数据点,900 000个数据点。在Intel Xeon E5-2609平台测试每个算法的加速率。实验每次随机产生2个相同大小的人工数据集,针对每个数据集,分别执行MC-K-means、PKMeans_MR、PKMeans_MT、K-means算法各10次,各算法每阶段各自共运行20次,最后分别记录下针对每个大小的数据集各算法聚类的平均时间。k的取值为5。实验结果如图 4所示,各算法加速率如图 5及表 1所示。
 |
| 图 4 算法线性测试Fig. 4 Scalability test of different algorithms |
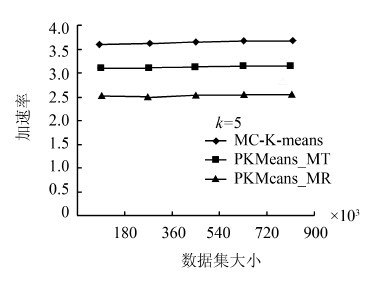 |
| 图 5 不同数据集大小下的加速率Fig. 5 Speedup rate of different data sizes |
|
Data Set Size/×103 |
MC-K- means | PKMeans_ MT | PKMeans_MR |
| 180 | 3.6 | 3.1 | 2.52 |
| 360 | 3.62 | 3.11 | 2.51 |
| 540 | 3.64 | 3.14 | 2.53 |
| 720 | 3.68 | 3.15 | 2.54 |
| 900 | 3.68 | 3.15 | 2.53 |
从实验结果可以看出,随着数据集规模的不断增长,各算法的运行时间均较为线性的增加。其中PKMeans_MR算法因为节点数并没有增加,所以加速率基本保持不变。MC-K-means以及PKMeans_MT的加速率均随着数据集规模的增加呈现提高的趋势,但都在接近各自极限后不再提高,保持一个相对稳定的加速率。这是因为随着数据集规模的增大,线程之间切换的资源消耗所占比重逐步降低,多核优势逐渐显现。
验证不同数据集大小情况下,不同的聚类数目k的取值对多核加速效率的影响。设置k为10,再次变换数据集大小从180K至900K,重复上述实验过程,记录实验结果如图 6所示,各算法加速率如图 7及表 2 所示。
 |
| 图 6 算法线性测试Fig. 6 Scalability test of different algorithms |
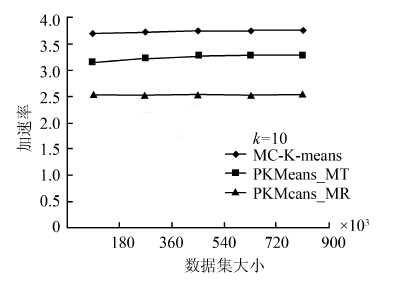 |
| 图 7 不同数据集大小下的加速率Fig. 7 Speedup rate of different data size |
|
Data Set Size/×103 |
MC-K- means | PKMeans_ MT | PKMeans_MR |
| 180 | 3.71 | 3.16 | 2.52 |
| 360 | 3.73 | 3.23 | 2.53 |
| 540 | 3.75 | 3.27 | 2.54 |
| 720 | 3.76 | 3.29 | 2.53 |
| 900 | 3.75 | 3.29 | 2.54 |
从实验结果可以看出,除PKMeans_MR算法因节点数不变,加速率保持相对稳定外,k取值的提高,有利于各并行化算法子任务的并行执行,减少同步,故提高了相应算法的加速率。
为了验证MC-K-means算法在执行过程中各并行化挖掘任务的负载是均衡的,在 i3-3240所在平台,修改聚类的过程为K-means读取数据集→MC-K-means读取数据集→K-means聚类→MC-K-means聚类。利用JDK7平台的jvisualvm[20]工具对生成的180K数据集的聚类全过程进行了监控,并记录如图 8所示。
 |
| 图 8 jvisual监控截图Fig. 8 Screenshot of jvisual |
使用UCI上的真实数据集Forest CoverType dataset对相关算法进行测试。该数据集共有581 012条记录,每条记录有54个维度,聚类时簇的个数设置为k=7。
该数据集较为庞大且聚类需多次迭代,挖掘耗时较多。在Xeon E5-2609所在平台,K-means算法完成聚类需要98.65 s,MC-K-means需要26.59 s,PKMeans_MT需要30.45 s,PKMeans_MR需耗时39.15 s;而在i3-3240所在平台,K-means算法完成聚类需要103.42 s,MC-K-means需要28.02 s,PKMeans_MT需要33.15 s,PKMeans_MR需耗时41.22 s。从图 9、10中可以看出,与人工生成数据集的测试结果类似,并行优化后的各算法在Xeon E5-2609平台获得了更高的加速比,且MC-K-menas算法依靠其更多执行步骤的并行化、更为直接的底层算法实现以及均衡的任务负载取得了最高的加速率。
 |
| 图 9 运行时间对比Fig. 9 Comparison of run time |
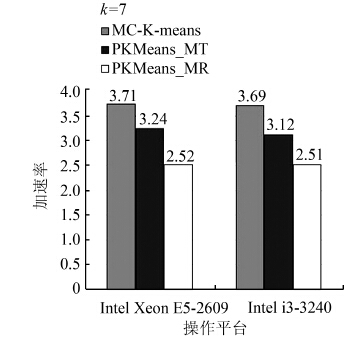 |
| 图 10 加速率对比Fig. 10 Comparision of speedup rate |
实验结果再次验证了MC-K-means算法可以在CPU的各核心之间均衡的负载各挖掘任务,充分利用现代CPU的多核计算能力,提高对大规模数据集的聚类效率。
5 结束语本文考虑到现阶段多核CPU的普及,针对经典的K-means算法进行了多核并行优化,提出了一种MC-K-means算法。该算法把K-means聚类任务按数据集等分为多个相互独立的挖掘子任务,并动态分配给多个线程并行执行,充分利用现代CPU的多核计算能力。实验结果证明了该算法可以充分利用现在的多核CPU,取得了较高的加速比,提高了聚类算法处理大规模数据集的能力。
虽然MC-K-means算法有着上述优势,但是当前版本的算法仍然存在一些问题,有待进一步改进。例如算法可以进一步扩展到集群聚类的领域。这些研究内容将在以后的研究过程中进一步补充完善。
| [1] | SUBRAMANIAM V. Programming concurrency on the JVM mastering synchronization, STM, and actors[M]. Beijing: China Machine Press,2013:1-27. |
| [2] | AARON B, TAMIR D E, RISHE N D, et al. Dynamic incremental K-means clustering[C]// Proc of the 2014 International Conference on Computational Science and Computational Intelligence, CSCI 2014. Los Alamitos, CA: IEEE Computer Society, 2014: 308-313. |
| [3] | SARMA T H, VISWANATH P, REDDY B E. Single pass kernel k-means clustering method[J]. Sadhana - Academy Proceedings in Engineering Sciences, 2013, 38(3): 407-419. |
| [4] | BRADLEY P, FAYYAD U, REINA C. Scaling clustering algorithms to large databases[R]. Redmond:Microsoft Research Report,1998:9-15. |
| [5] | 陈光平,王文鹏,黄俊. 一种改进初始聚类中心选择的K-means算法[J]. 小型微型计算机系统,2012,33(6): 1320-1323. CHEN Guangping, WANG Wenpeng, HUANG Jun. Improved initial clustering center selection method for k-means algorith[J]. Journal of Chinese Computer Systems, 2012, 33(6): 1320-1323. |
| [6] | MAHMUD M S, RAHMAN M M, AKHTAR M N. Improvement of k-means clustering algorithm with better initial centroids based on weighted average[C]//Proc of the 7th International Conference on Electrical and Computer Engineering, ICECE 2012. Los Alamitos, CA: IEEE Computer Society, 2012: 647-650. |
| [7] | PATIL R, JONDHALE K C. Edge based technique to estimate number of clusters in k-means color image segmentation[C]//Proc of the 3rd IEEE International Conference on Computer Science and Information Technology, ICCSIT 2010. Piscataway, NJ: IEEE Computer Society, 2010: 117-121. |
| [8] | JING Liping, NG M K, HUANG zhexue. An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(8): 1026-1041. |
| [9] | BISHNU P S, BHATTACHERJEE V. A dimension reduction technique for k-means clustering algorithm[C]//Proc of the 1st International Conference on Recent Advances in Information Technology, RAIT-2012. Piscataway, NJ: IEEE Computer Society,2012: 531-535. |
| [10] | DOBBELIN R, SCHUTT T , REINEFELD A. An analysis of SMP memory allocators: mapreduce on large shared-memory systems[C] //Proc of the 41st International Conference on Parallel Processing Workshops (ICPPW), 2012. Piscataway, NJ: IEEE, 2012: 48-54. |
| [11] | DI F G, BLASA F, CAFIERO S, et al. Fault tolerant decentralised k-means clustering for asynchronous large-scale networks[J]. Journal of Parallel and Distributed Computing, 2013, 73(3): 317-329. |
| [12] | 赵卫中,马慧芳,傅燕翔,等.基于云计算平台Hadoop的并行k-means聚类算法设计研究[J].计算机科学,2011,38(10): 166-169. ZHAO Weizhong, MA Huifang, FU Yanxiang, et al. Reasearch on parallel k-means algorithm design based on hadoop platform [J] . Computer Science, 2011,38(10): 166-169. |
| [13] | 王晓华. MapReduce 2.0源码分析与编程实战[M].北京:人民邮电出版社, 2014:1-55. |
| [14] | MARTHA, V, ZHAO Weizhong, XV Xiaowei. H-MapReduce: A framework for workload balancing in MapReduce[C]// Proc of the International Conference on Advanced Information Networking and Applications, AINA. Piscataway, NJ: IEEE, 2013: 637-644. |
| [15] | ZHAO Weizhong, MA Huifang, HE Qing. Parallel k-means clustering based on mapreduce[C]//Proc of the 1st International Conference on Cloud Computing, CloudCom 2009. Germany: Springer Verlag, 2009: 674-679. |
| [16] | FAHIM A M. Parallel implementation of k-means on multi-core processors[J]. Computer Science and Telecommunications, 2014, 1(41): 53-61. |
| [17] | ZALIK K R. An efficient k-means clustering algorithm[J]. Pattern Recognition Letters, 2008, 29(9): 1385-1391. |
| [18] | HERBERT S, DALE S. A comprehansive introduction[M]. Beijing: China Machine Press, 2013 |
| [19] | JAVIER F G. Java 7 concurrency cookbook[M]. Beijing: Posts Telecom Press, 2014. |
| [20] | Monitoring and managing java se 6 platform applications[EB/OL].[2005-12-18]http://java.sun.com/developer/technicalArticles/J2SE/monitoring. |



