飞机液压管道振动过大是影响飞行安全的一个重要因素,飞机液压泵的固有频率接近流体管路的谐振频率时,流体压力脉动与充液管道谐振是不可避免的,此时流体压力脉动加强,而且长时间谐振会导致管道疲劳破裂[1]。
液压管道传统支撑方式采用刚性系数较大的卡箍,使充液管道固有频率高于泵源输油的脉动频率。但随着飞机高功率、大流量的需求,现代液压泵转速有了较大提高,因此泵源脉动频率也在提高,传统的卡箍类型以及布局方式已经不能满足要求。如果单纯考虑增大管道卡箍的刚度或数量使充液管道固有频率上升,会使更多的管道振动传递到其固定桁架上,不利于隔振。刚性卡箍内圈加橡胶垫虽然可以增大一定的阻尼性,但由于橡胶高温易老化,不宜长时间使用。前苏联在飞机发动机管道上采用了金属橡胶卡箍,取得了很好的隔振效果,并延长了卡箍使用寿命。国内飞机液压管道上目前还未采用这种材料,因此本文针对应用到液压管道上的金属橡胶卡箍进行隔振理论分析、比较及优化。
金属橡胶是萨玛拉国立航空航天大学[2]在20世纪60年代研制出的一种高阻尼非线性减振材料,是将金属丝有序排放后冲压成型,其内部类似于橡胶高分子网状结构,金属丝之间的干摩擦可以耗散振动能量,但较普通橡胶具有承载能力高、耐油、耐腐蚀、耐高低温且不易老化等优点[3],因此早已在前苏联多种型号飞机上应用。
哈尔滨工业大学金属橡胶技术研究开发中心是国内较早开展对金属橡胶研制的单位,姜洪源课题组[4, 5, 6]推导出金属橡胶构件的刚度、弹性力、摩擦力及强度计算公式、能量耗散系数及阻尼系数的近似计算公式。开展了金属橡胶构件理化性能、动静态试验和单向、双向承载及强化寿命等试验研究,获得了主要参数间的相互关系,并分析了金属橡胶隔振器相对密度、预变形及所加试验量级对金属橡胶隔振系统的影响,研究表明相对密度及预变形越大导致金属橡胶刚度越大,使隔振系统加速度响应值变大。此外,北航[7]、军械工程学院[8]等高校也研究了金属橡胶吸声、隔振理论及试验特性,并设计出相应的产品。
Ertas[9, 10]分析了在变激励幅值,变激励频率以及静态偏心工况下的金属橡胶阻尼器的非线性刚度以及阻尼特性,将金属橡胶应用到径向滑动轴承上,使其承载能力和有效阻尼率增大。
针对非线性隔振器性能研究,彭献[11]以线性阻尼、立方刚度非线性系统为例,分析了主动隔振与被动隔振状态下非线性刚度系数对隔振传递率的影响。针对迟滞摩擦系统,Iwan[12]等提出了双折线模型去描述记忆非线性恢复力。魏浩东、肖然[13, 14]等针对金属橡胶减振器建立了非线性模型,主要通过试验对模型进行参数辨识,并设计了相应的金属橡胶减振器应用到实际中。
以往对金属橡胶隔振器的研究主要从试验角度出发,去辨识其非线性刚度、阻尼及干摩擦系数,并通过改变金属橡胶的预紧力和相对密度分析对其隔振效果的影响,但并未从理论角度去验证非线性刚度以及记忆恢复力对金属橡胶隔振传递率的影响。本文采用三次非线性刚度以及双折线记忆恢复力模型,针对液压系统管道特殊结构以及高激振源频率工况下分析了非线性刚度以及干摩擦记忆恢复力对隔振传递率的影响,并将结果与文献的试验结论相对比,同时,采用改进粒子群算法针对飞机飞行剖面对金属橡胶隔振参数进行优化,为其在液压系统管道隔振的应用做了一定的理论铺垫。
1 金属橡胶隔振数学建模金属橡胶隔振器在飞机液压管道上的应用如图 1所示,从图 1看出,金属橡胶放置在外围卡箍的凹槽内,传统管道固定一般直接与外围卡箍接触或之间有薄的橡胶垫作为隔振装置。
 |
| 图 1 飞机液压管道卡箍示意图 Fig. 1 Sketch of hydraulic pipe clamp in aircraft |
图 2为金属橡胶卡箍隔振原理示意图,考虑3次非线性刚度,在duffing模型基础上增加了金属橡胶的干摩擦记忆恢复力进而得到了振动方程:
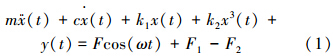
式中:m为充液管道的质量;Fcos(ωt)为流体脉动对管道的激励力;x(t)为管道在激励力和卡箍阻力下的位移;k1为线性刚度系数,k2为非线性刚度系数;c为粘性阻尼系数,与位移有关的非对称高次弹性力和与速度有关的粘性阻尼力被认为是无记忆恢复力;y(t)为金属橡胶变形过程中的干摩擦记忆恢复力;F1,F2分别是截取管道两端的剪切力,但由于液压管道内流体压力高达28 MPa,因此,F1-F2可以被忽略。
 |
| 图 2 金属橡胶隔振示意图 Fig.2 Vibration isolation sketch of metal rubber |
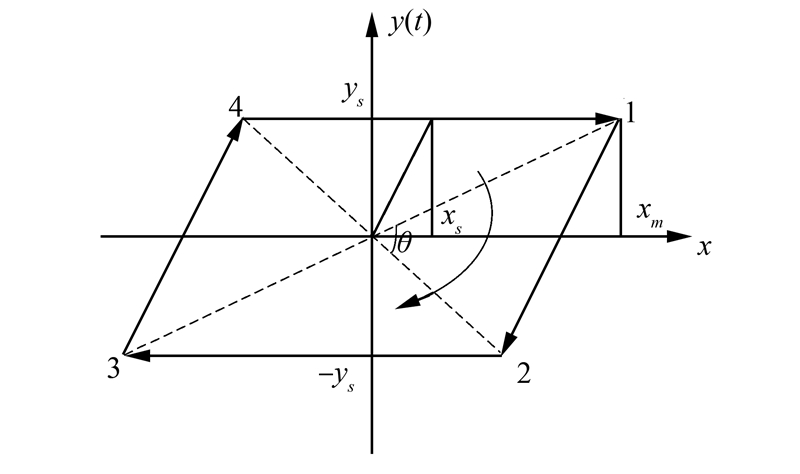
对于干摩擦力,在外力作用时,首先产生弹性变形,当外力增大到一定程度后,两金属丝产生相对滑移,这时就产生了迟滞摩擦。Iwan[10]基于此将干摩擦表面看成一根弹簧与一个理想库伦摩擦副的串联组合,并提出了双线性迟滞恢复力模型,其具有记忆特性的非线性记忆恢复力y(t),一般采用双折线模型表示,如图 3所示。
 |
| 图 3 双折线迟滞关系模型 Fig. 3 Double broken line hysteresis model |
图中:ys是干摩擦非线性滑移后的恢复力,xs是开始滑移时的变形值,xm是最大变形量,ks是滑移前的线性刚度,且ks=ys/xs。记忆恢复力的增量形式数学表达式为
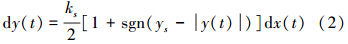
设x(t)=Xcos(ωt-φ),引入坐标变换τ=t-tξ,tξ=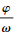 ,则x(t)=Xcos(ωτ),由关系式Xcos θ=X-2xs得到θ=arccos(1-
,则x(t)=Xcos(ωτ),由关系式Xcos θ=X-2xs得到θ=arccos(1- ),根据图 3所示,将双折线模型划分为4个阶段:
),根据图 3所示,将双折线模型划分为4个阶段:
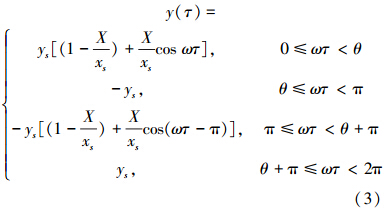
对上述周期函数做傅里叶变换,并取一阶近似,则
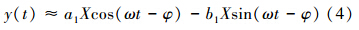
式中: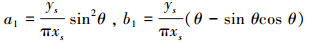 。
。
由以上推导,令x(t)=Xcos(ωt-φ),式(1)变为
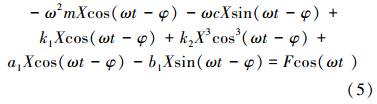
对式(5)进行无量纲变化,令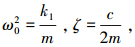
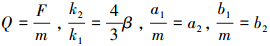 ,则式(5)变为
,则式(5)变为
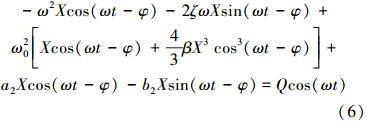
根据基波平衡原理,由式(6)得
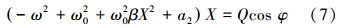
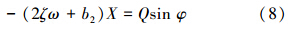
令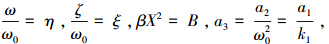 b3=
b3=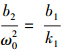 。
。
已知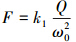 ,则激励力的基波幅值F为
,则激励力的基波幅值F为
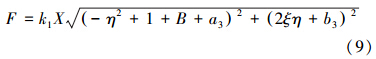
传递到基础上的力fT:
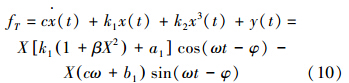
传递到基础上力的基波幅值FT为
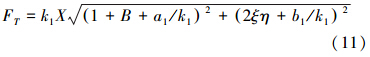
金属橡胶的隔振传递率ψA为
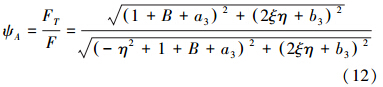
从金属橡胶隔振传递率模型(12)可以看出,隔振传递率ψA主要与B、ξ、a3、b3相关。如果隔振器线性系数k1确定,隔振传递率ψA主要与金属橡胶的非线性刚度系数k2,阻尼系数c以及干摩擦记忆恢复力参数a1、b1有关,由于B、ξ、a3、b3与k2、c、a1、b1呈线性关系,因此其变化规律可以间接代表k2、c、a1、b1。阻尼率ξ对隔振传递率的影响已在经典振动理论表述过,不做赘述。a3与b3的变化相关联,因此改变a3、B两个参数,分析其与隔振传递率关系。
2.1 干摩擦记忆恢复力对隔振传递率的影响干摩擦记忆恢复力是金属橡胶隔振器与传统非线性隔振器额外增加的部分,从双折线迟滞模型推导来看,干摩擦记忆恢复力主要由ys、xs决定,反映到隔振率表达式(12)中,参数a3、b3确定干摩擦记忆恢复力对隔振率的影响,同时a3、b3也具有相关性。因此,根据文献[15]参数辨识结果,假设a3从0.01~0.3之间线性变化,通过设置不同阻尼率ξ仿真对比刚性金属卡箍、带柔性橡胶隔振垫卡箍(简称柔性橡胶卡箍,flexible rubber clamp)以及带金属橡胶隔振垫卡箍(简称金属橡胶卡箍,metal rubber clamp)三者的隔振率特性。
从图 4可以看出,在激振源低频阶段,刚性金属卡箍的隔振传递率效果最差,反而会将振动扩大传递到基础上,而柔性橡胶卡箍与金属橡胶卡箍较刚性金属卡箍有所改善;高频阶段,刚性金属卡箍的隔振传递率降到最低,但根据飞机的整个飞行剖面分析,激振源频率与充液管道固有频率比值一般不会大于2。在飞机巡航阶段下的频率比在1.3~1.4附近,通过对比3种形式的卡箍,柔性橡胶卡箍虽然在飞机巡航特定频率段隔振效果较好,但由于其不耐高温,易老化,一般不会单独使用;金属橡胶在隔振传递率方面具有与普通橡胶同样的优势,而刚性金属卡箍在低频段隔振效果差同样不宜单独使用,因此综合以上分析金属橡胶卡箍隔振特性最好。下面单独分析金属橡胶卡箍隔振方程中干摩擦记忆恢复力参数a3变化对隔振传递率的影响。
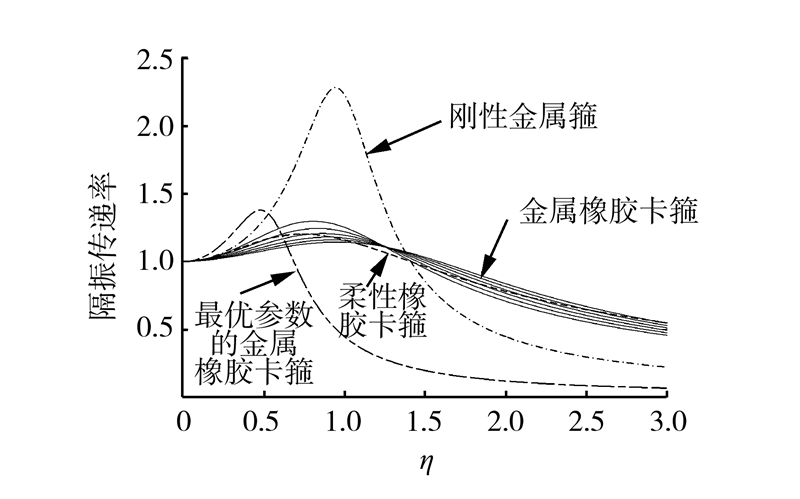 |
| 图 4 三类卡箍隔振传递率比较 Fig. 4 Isolation rate comparison of three kinds of clamp |
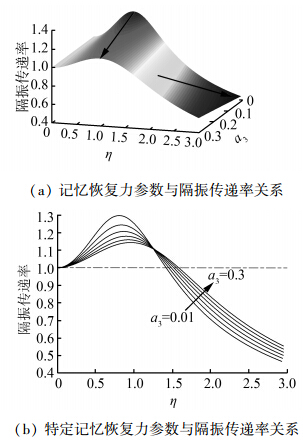
由图 5(a)可看出,在低频段,a3越小隔振率越高,隔振效果越差;在高频段,a3越小隔振效果越好。图 5(b)选取了a3分别为0.01、 0.06、 0.11、 0.16、 0.21及0.3这6个特征值的隔振率变化,并得到隔振率变化曲线交汇点及其所对应的频率比1.273,这与其他参数选取有密切关系。根据式(4)以及参数a3、b3与a1、b1呈线性关系得知,a3与b3反映了金属橡胶滑移前线性刚度大小,而金属橡胶滑移前的线性刚度与金属橡胶的预变形量成正比,在隔振率小于1时,预变形量越大,隔振效果越差,文献[6]通过试验分析了不同预变形量下系统的振动加速度响应,试验分析结果与本文理论结果一致。因此针对不同激振源频率可对金属橡胶施加不同预变形量使其隔振率最低,在文中第3部分将对隔振率参数做优化。
 |
|
图 5 记忆恢复力参数对隔振传递率影响
Fig. 5 Influence of memory restoring force parameters on vibration isolation rate |
非线性刚度参数B的增大反映了金属橡胶刚度由“软簧”到“硬簧”的变化,根据文献[11],当三次非线性刚度系数为负时为“软簧”,当三次非线性刚度系数为非负时为“硬簧”。通过文献[15]对金属橡胶模型参数辨识结果,令B取[-1, 1]区间,代入式(12)得到隔振率如图 6所示。
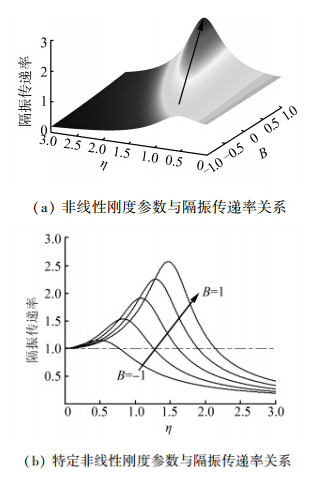 |
| 图 6 非线性刚度参数对隔振传递率影响 Fig. 6 Influence of nonlinear stiffness parameters |
从图 6可以看出,图 6(a)反映了隔振率随着频率比η和非线性刚度参数B的变化过程,明显可以看出,隔振率峰值随着B递增而单调上升,因此,图 6(b)提取出了当B分别为-1、-0.5、0、0.5、1情况下的隔振率,从图中可以看出,当激振源处于低频阶段,金属橡胶为硬簧时隔振效果较好,高频阶段软簧的隔振效果较好。飞机在巡航阶段下的频率比在1.3~1.4附近,因此软簧隔振效果要更好。金属橡胶的非线性刚度参数B与其相对密度相对应,在隔振率小于1时,相对密度越大隔振效果越差,文献[6]通过试验分析了不同相对密度下系统的加速度振动响应的变化,分析结果与本文的理论仿真结果一致。
3 基于飞机飞行剖面下的金属橡胶隔振传递率计算图 7所示为某型号飞机飞行剖面示意图,从图中可以看出,飞机主要在巡航转速下飞行,机动飞行时间较少,因此发动机处于全转速阶段时间较少,大约占23%;准备着陆和慢车停止阶段时发动机为65%转速,大约占8%;其余飞机发动机均处于80%转速,占69%。
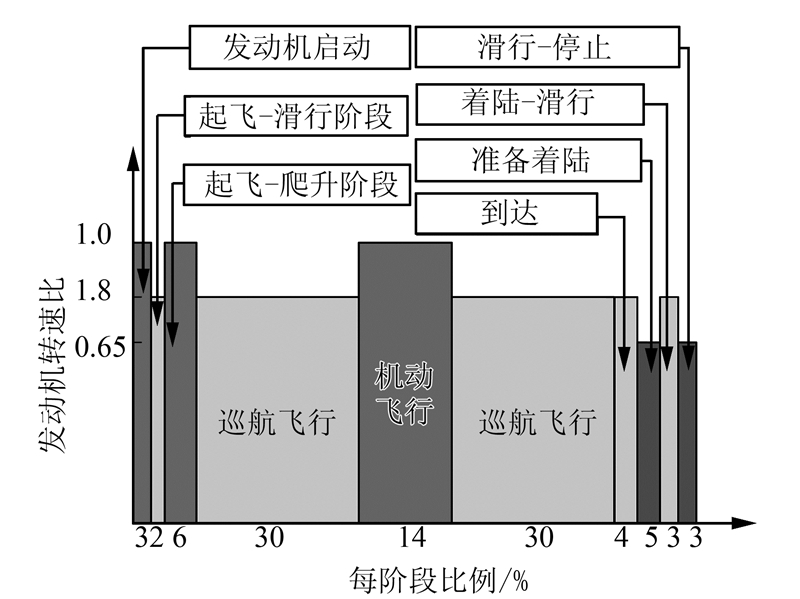 |
| 图 7 某型号飞机飞行剖面 Fig. 7 Flight profile of a certain type of aircraft |
不同的转速对应不同的激振源频率,该型号飞机液压泵柱塞数z为9,额定转速n为4 000 r/min,则激振源频率f=nz/60,并且已知充液管道的固有频率为360 Hz,表 1为不同飞行剖面下所对应的频率比η。
| 转速 /min | 激振源频率 /Hz | 频率比 |
| 4 000 | 600 | η1=1.67 |
| 3 200 | 480 | η2=1.33 |
| 2 600 | 390 | η3=1.08 |
根据图 7所示的飞行剖面可以得到该工况下金属橡胶的隔振率加权和,如式(13)所示。 通过算法在一定范围内优化式(12)中参数B、ξ、a3、b3,使式(13)隔振率的加权和降到最低。
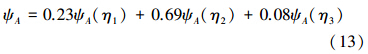
式中:η1、η2、η3分别是全转速、80%转速和65%转速的激振源频率与管道固有频率比值。
4 基于改进粒子群算法的金属橡胶隔振参数优化 4.1 基于飞机飞行剖面下的金属橡胶隔振传递率计算粒子群算法[16]是由Eberhart与Kennedy在1995年提出的,其基本思想是初始化一群随机粒子,在每一代中选取个体最优点,同时与其他代的个体最优点进行比较选取全局最优点,确定两个最优点后,粒子以式(14)和式(15)更新自己的速度和位移,设定迭代的步数后,使目标函数的值收敛于某一点。
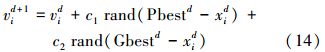
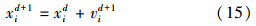
式中:vid为粒子i在第d代中的速度;xid为粒子i在第d代中的位置;c1、c2为学习因子,选择合适的c1、c2可以使粒子加速收敛且不陷入局部最优;rand1d、rand2d分别为[0, 1]之间的随机数;Pbestid为第d代中个体最优点;Gbestd为第d代后的全局最优点。
传统粒子群算法优势在于有较快的收敛速度但并不能完全保证取到全局最优值,对粒子群算法的改进一般主要有惯性权重法[17]、压缩因子法[18]、空间邻域法[19]等,本文考虑了c1、c2对优化结果的影响,从式(14)可以看出,当c1过大时,可以扩大粒子寻优范围,适合粒子在初期阶段进行大范围的搜索,避免很快陷入局部最优;当c2过大时,最优粒子在前期收敛很快,但很容易陷入局部最优,但在后期如果增大c2时,可以固定全局变量,提高收敛速度。传统粒子群算法将c1、c2取2[16],本文尝试将c1、c2分别设为线性递减和线性递增变化。令c1在[2.2,1.8]线性递减变化,令c2在[1.8,2.2]线性递增变化。同时将模拟退火算法[20]引入对最优值的判断,模拟退火法根据实际固体退火原理,将固体粒子加温至无序状,通过冷却使各粒子达到平衡,内能降到最低,其中初始温度T0取决于粒子群优化第一代的最优值,令退火速率α为0.8,温度的改变为Td+1=αTd。模拟退火算法与粒子群算法的结合在理论上既保证了粒子群的快速收敛优势同时避免陷入局部最优点。改进后的粒子群算法流程如图 8所示。
4.2 基于改进粒子群算法的参数寻优从图 8中看出,令式(13)为目标函数,fitness(Pbest)代表个体最优点的隔振率加权和,fitness(Gbest)代表全局最优点的隔振率加权和。T代表模拟退火温度,根据文献[12, 13]对金属橡胶模型参数辨识结论,分别选取B∈[-1,1],ξ∈[0.001,0.1],a3∈[0.01,0.3],b3∈[0.01,0.3],对上述4个参数在区间范围内寻优过程如图 9所示。
 |
| 图 8 改进粒子群算法流程示意图 Fig. 8 Flow chart of modified particle swarm optimization |
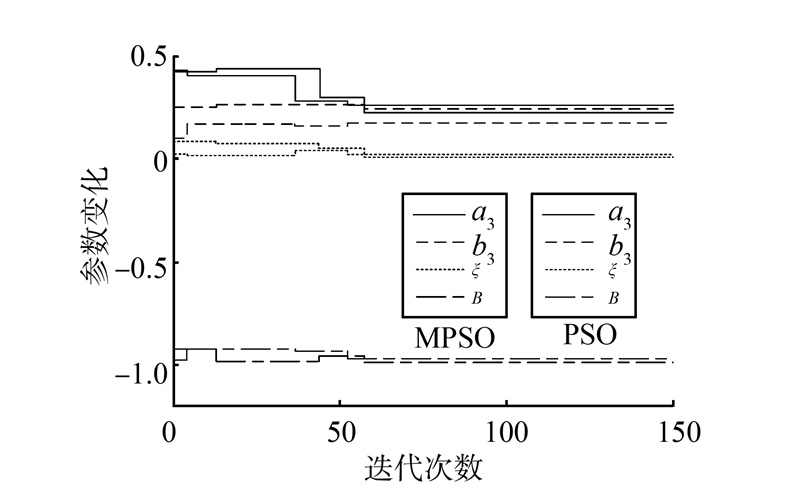 |
| 图 9 参数迭代变化示意图 Fig. 9 Sketch of parameters variation with iteration |
图 9为常规粒子群算法与本文改进粒子群算法的优化过程,从图中可以看出,常规粒子群算法在第52步收敛,此时,B=-0.934 4,a3=0.243 1,b3=0.195 4,ξ=0.047 4,ψA最小值为0.285 4;而改进后的粒子群算法在第58步收敛,得到B=-0.987 2,a3=0.227 3,b3=0.235 6,ξ=0.012 9,ψA最小值为0.222 2。通过优化仿真得知,传统粒子群算法陷于局部最优,而改进粒子群算法收敛速度虽然略慢于传统粒子群算法,但避免陷入局部最优解,验证了改进的效果,同时得到了最小的隔振率以及相对应的金属橡胶隔振器参数,将优化后的参数代入式(12)并与图 4对比,如图 10所示。
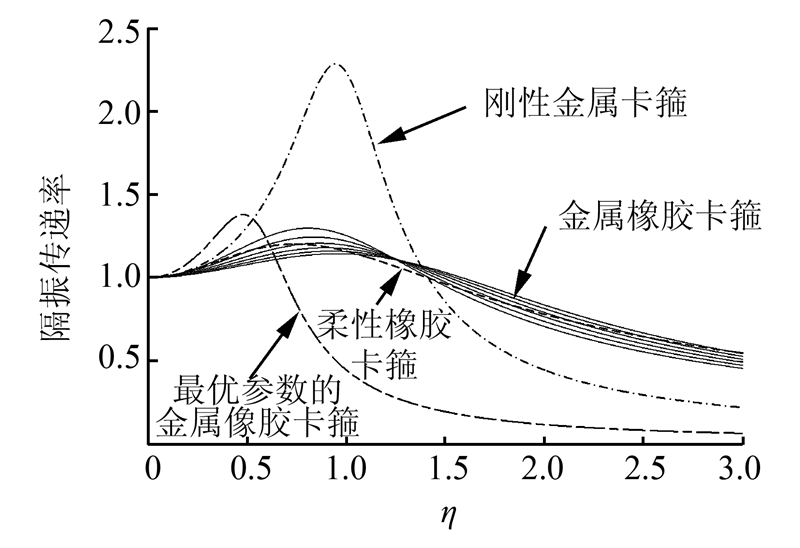 |
| 图 10 参数优化后的卡箍隔振传递率对比 Fig. 10 Isolation rate comparison with optimized clamp |
通过图 10可以看出,根据表 1对比频率比η大于1的隔振率,参数优化后的柔性卡箍隔振率最低,验证了优化的有效性,对于设计飞机液压管道金属橡胶卡箍具有理论指导意义。
5 结束语本文针对飞机液压管道的金属橡胶卡箍隔振,建立了考虑三次非线性刚度以及干摩擦记忆恢复力的振动模型,分析了非线性刚度与记忆恢复力对隔振传递率的影响,并通过改进粒子群算法优化了模型参数,使其隔振传递率降到最低。具体结论如下:
1)金属橡胶卡箍在飞机巡航阶段的隔振传递率与柔性橡胶卡箍类似,但较普通橡胶有耐高温、耐腐蚀、寿命长等优点,且其对管道支撑刚度远高于普通橡胶;
2)记忆恢复力参数a3与b3反映了金属橡胶滑移前线性刚度大小,在低频段,其滑移前线性刚度越小隔振传递率越高,隔振效果越差;在高频段,滑移前线性刚度越小隔振效果越好。
3)非线性刚度参数B反映了金属橡胶刚度由“软簧”到“硬簧”的变化,当在激振源处于低频阶段,金属橡胶为硬簧时隔振效果较好,高频阶段软簧的隔振效果较好。
4)改变常规粒子群算法的学习因子变化规律并采用模拟退火思想作为判断最优点更新依据可以避免算法陷入局部最优且能提高收敛速度,并依据改进后算法得到了金属橡胶卡箍模型隔振传递率最低的参数配置,下一步工作还需要对优化结论进行试验验证。
| [1] | 王占林.飞机高压液压能源系统[M].北京:北京航空航天大学出版社,2004:21-30. |
| [2] | ЧЕΓОДАЕВ Д Е,МЧЛЮКИН О П,КОЛТЬIГИН Е В著.金属橡胶构件的设计[M].李中郢,译.北京:国防工业出版社,2000:1-13. |
| [3] | 董秀萍,张力.新型材料-金属橡胶建模及应用[M].北京:化学工业出版社,2010:1-16. |
| [4] | 姜洪源,夏宏宇,敖宏瑞,等.金属橡胶构件的性能分析与实验研究[J].中国机械工程,2001,12(11):94-97.JIANG Hongyuan,XIA Hongyu,AO Hongrui,et al.Experimental research on characteristics of metal rubber element[J].China Mechanical Engineering,2001,12(11):94-97. |
| [5] | 姜洪源,敖宏瑞,夏宏宇,等.金属橡胶隔振器干摩擦阻尼特性的研究[J].机械设计,2002,19(11):11-14.JIANG Hongyuan,AO Hongrui,XIA Hongyu,et al.Research on dry friction damping characteristics of metallic rubber vibration isolator[J].Journal of Machine Design,2002,19(11):11-14. |
| [6] | 闫辉,姜洪源,刘文剑,等.金属橡胶隔振器随机振动加速度响应分析[J].物理学报,2010,59(6):4065-4069.YAN Hui,JIANG Hongyuan,LIU Wenjian,et al.Analysis of acceleration response of metal rubber isolator under random vibration[J].Acta Physica Sinica,2010,59(6):4065-4069. |
| [7] | 马艳红,李昊宇,李一峰,等.金属橡胶材料吸声特性试验与分析[J].北京航空航天大学学报,2009,35(5):604-607.MA Yanhong,LI Haoyu,LI Yifeng,et al.Experiment and analysis on sound absorption characteristics of metal rubber[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(5):604-607. |
| [8] | 李冬伟,白鸿柏,杨建春,等.金属橡胶动力学建模及参数识别[J].振动与冲击,2005,24(6):57-60.LI Dongwei,BAI Hongbai,YANG Jianchun,et al.Database system of network based remote monitoring and fault diagnosis system[J].Journal of Vibration and Shock,2005,24(6):57-60. |
| [9] | ERTAS B H.Nonlinear dynamic characterization of oil-free wire mesh dampers[J].Journal of Engineering for Gas Turbines and Power,2008,130(3):1-8. |
| [10] | ERTAS B H.Compliant hybrid journal bearings using integral wire mesh damps[J].Journal of Engineering for Gas Turbines and Power,2009,131(2):1-11. |
| [11] | 彭献,唐驾时.非线性隔振理论初探[J].振动与冲击,1996,15(4):13-17,36.PENG Xian,TANG Jiashi.Research on theory of nonlinear vibration isolation[J].Journal of Vibration and Shock,1996,15(4):13-17,36. |
| [12] | WAN W D.The dynamic response of bilinear hysteretic system[D].California:California Institute of Technology,1961:1-50. |
| [13] | 魏浩东.金属橡胶构件抗冲击性能的理论及实验研究[D].哈尔滨:哈尔滨工业大学,2007:1-60.WEI Haodong.Theoretical and experimental research on metal rubber element anti-shock performance[D].Harbin:Harbin Institute of Technology,2007:1-60. |
| [14] | 肖然.金属橡胶减振器的非线性特性研究及应用[D].太原:中北大学,2009:1-50.XIAO Ran.The study and application on non-linear character of metal-rubber vibration absorber[D].Taiyuan:North University of China,2009:1-50. |
| [15] | 廖云飞.金属橡胶阻尼器滞回性能及其耗能减振结构模型试验研究[D].哈尔滨:哈尔滨工业大学,2010:1-60.LIAO Yunfei.Metal rubber damper hysteresis and passive dissipation structural model research[D].Harbin:Harbin Institute of Technology,2010:1-60. |
| [16] | KENNEDY J,EBERHART R C.A discrete binary version of the particle swarm algorithm[C]//Proceedings of IEEE International Conference on Systems Man and Cybernetics.Piscataway:IEEE Press,1997:4104-4108. |
| [17] | SHI Y,EBERHART R C.A modified particle swarm optimizer[C]//IEEE World Congress on Computational Intelligence.Anchorage:IEEE Press,1998:69-73. |
| [18] | CLERC M.The swarm and queen:towards a deterministic and adaptive particle swarm optimization[C]//Proceeding of the congress on Evolutionary Computation.Piscataway:IEEE Press,1999:1951-1957. |
| [19] | SUGANTHAN P N.Particle swarm optimizer with neighborhood operator[C]//Proceedings of the Congress on Evolutionary Computation.Piscataway:IEEE Press,1999:1958-1961. |
| [20] | KIRKPATRICK S,GELATT Jr C D,VECCHI M P.Optimization by Simulated Annealing[J].Science,1983,220(4598):671-680. |



