2. 语音及语言信息处理国家工程实验室, 安徽 合肥 230026;
3. 中国科学院 合肥智能机械研究所, 安徽 合肥 230026
2. National Laboratory of Speech and Language Information Processing, Hefei 230027, China;
3. Institute of Intelligent Machine, Chinese Academy of Sciences, Hefei 230027, China
随着日渐成熟的计算机水平的发展,根据视觉的人体的运动跟踪和运动剖析逐渐成为当今计算机视觉学科的科研热门,同时人机交互、基于运动的识别、虚拟现实等有关领域[1, 2]的迫切需求也推动此方向的飞速进展,推动了大量的研究人员加入这个领域的研究。
本文在综合考虑跟踪效果和计算效率的情况下,提出了一种简单高效、且不牺牲跟踪结果质量的基于棍状模型的算法。
1)本文对基于逆向运动跟踪算法的关节位置预测方法和旋转角计算方法进行了改进。关节位置预测方法的优劣会影响跟踪算法效率和有效性。基于逆向运动跟踪算法做了关节的运行模式是速度不变的假设,而真实的跟踪过程中关节运动模型是变速且带有随机性的,会导致局部寻优较慢;当预测位置出现较大偏差,关节不在寻优区域时,会导致找不到准确的关节位置。因此,采用了粒子滤波的方式对关节位置进行预测,提高了跟踪的有效性。
2)文中同时提出了利用3dmax生成序列图片作为测试样本,将跟踪结果与3dmax得到的真实数据进行比较的验证方法。其中,图片序列的生成过程采用根据已知运动目标的关节位置,生成人体的动作序列,进而生成实验所需视频。然后,使用传统算法与本文算法在生成所得视频基础上进行运动目标的跟踪,从而获得运动目标的最优估计值。最后将估计值与原始的真实值比较,通过计算人体各关节图像空间的像素值偏差,说明本文算法的有效性。
1 人体骨骼及外观模型本节介绍本文所用的人体骨骼模型和人体外观模型及对相关名称进行解释。
1)人体骨骼模型如图 1所示。本文将人体看成是一种棍状树型模型,其包含15节身体片与8对关节。其中,根节点J1对应人体骨骼结构的盆骨;Ji对应的人体位置,如图 1所示。文中在人体骨骼模型上定义了2种坐标系:(a)局部坐标系,坐标系的原点为相应关节,坐标系方向,如图 2右上方所示;(b)基坐标系。此坐标系的中心点为J1关节。它的轴向与系统开始状态下J1局部坐标系的轴向保持相同。文中用欧拉角[15]来标识关节的旋转,它的公式是α,β,γ,其中α表示绕x轴旋转角度,β表示绕y轴旋转角度,γ表示绕z轴旋转角度。
 |
| 图 1 人体骨骼和关节模型 Fig. 1 The human bone model and joint model |
 |
| 图 2 人体外观模型 Fig. 2 Rep of human body’s appearance model |
2)人体外观模型。人体外观模型由外观形状模型及外观纹理模型构成。如图 2所示,人体外观模型共由一些矩形块构成。每个矩形对应人体的一节身体片段。矩形由人体段内部的像素值构成,其中相对坐标是形状模型及像素值是纹理模型。
3)摄像机成像模型。三维空间中某点的坐标值与该点在二维投影平面上的坐标(u,v)满足以下方程:
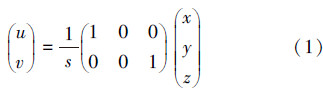
参数s是反比例因子,根据公式 计算得到[16]。此公式中,f是相机的焦距,z是此点的相机透视空间深度坐标。从式(1)可知,Δs=TΔz,即Δs与Δz成正比例。
计算得到[16]。此公式中,f是相机的焦距,z是此点的相机透视空间深度坐标。从式(1)可知,Δs=TΔz,即Δs与Δz成正比例。
不失一般性,本文讨论人身体各个关节运动的问题。本文算法框图如图 3所示,包含下面4步。
 |
| 图 3 算法框架图 Fig. 3 Diagram of the ALG framework |
1)跟踪系统初始化。使用者根据跟踪系统提供的输入界面来确定人体骨骼模型和外观模型。如图 4,外观模型是人体各段的像素信息。该部分输入为视频第一帧图像,由使用者在其上标识出的关节点位置计算出人体外观模型及人体骨架模型[17]中各身体部分的相对尺寸。
 |
| 图 4 标注后的视频首帧 Fig. 4 The video’s Fst-frame after annotation |
2)求旋转欧拉角。按照树形化方式[18],如图 1右图。由待计算关节的预测的在二维图像中的位置,借助逆向运动学模型计算出此关节所在人体片段的旋转角度。第一步依据人体各部分相对比值计算出此关节在透视相机模型下相应的立体空间坐标。第2步根据改进的逆向运动学计算出旋转角。
3)求关节在图像中的位置。根据上一步获得的关节旋转欧拉角依照正向运动学[8]计算出此关节所在的人体片段中所有像素旋转后的立体坐标值。最后根据摄像机投影模型把人体片段投影到二维平面。从而计算出待计算的关节点相应的人体片段在二维平面上的坐标值。因此,获得形变身体段。
4)直方图匹配。将形变身体段与系统初始化时得到的外观模型做直方图匹配。在相似度为极大值时,我们把相应的关节位置当做计算出的最准确的关节位置。同时,此时由所有人体关节位置重构的人体形态为实验最准确的形态。
本文不对步骤1)~4)进行详细叙述,如有需要请参考邹北骥[14]的相关文章。
3 算法改进 3.1 计算旋转角方法的改进逆向运动学算法计算旋转欧拉角的方法,其假定当Ji∈J4,J7,J10,J13时,绕y轴旋转分量α=0;否则,绕x轴旋转分量β=0;即必须加上绕y轴或者绕x轴旋转分量为零的约束。在跟踪过程中,人体的主要关节或多或少都会沿某个轴向发生旋转,上述约束是不符合真实情况的,所以计算出的旋转角是有误差的。基于此缺陷本文找到了一种精确计算旋转角的方法[9]。
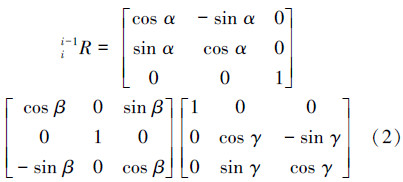
如图 5所示,在三维空间中,可以知道旋转可以通过3个欧拉角(α,β,γ)来定义,欧拉旋转定理表明,任意2个具有相同原点的三维空间坐标系变换,可以通过绕一包含原点的固定轴进行相应旋转来实现。这里的转动参量是由旋转角度和那条固定的旋转轴(即欧拉角和欧拉轴)来表示的。
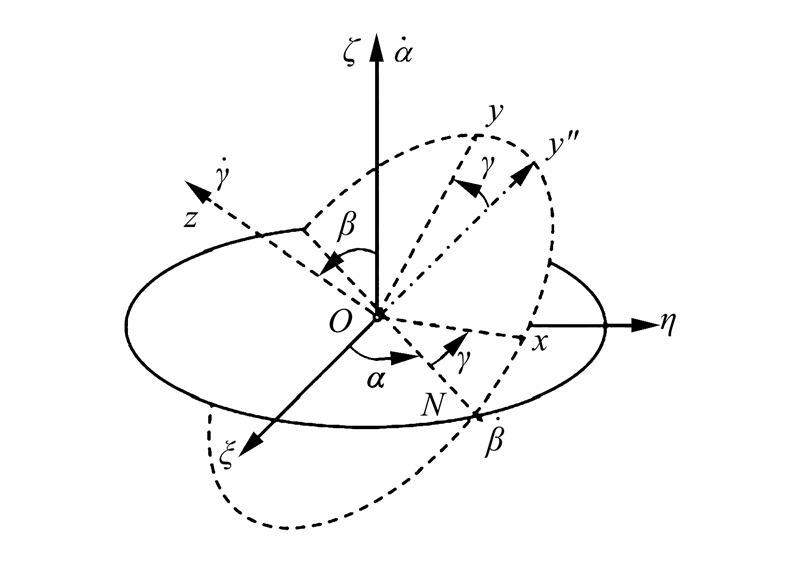 |
| 图 5 欧拉角示意图 Fig. 5 Euler Angle diagram |
如图 6所示,三维空间中有一初始矢量为r(OP),绕欧拉轴转动后变为r′,n为欧拉轴的单位向量,φ表示r(OP)到 (OQ)的旋转角,n与φ的求解方式是2个向量的叉乘为欧拉轴,点乘为旋转角的余弦。具体求解公式为
(OQ)的旋转角,n与φ的求解方式是2个向量的叉乘为欧拉轴,点乘为旋转角的余弦。具体求解公式为
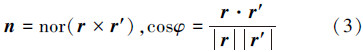
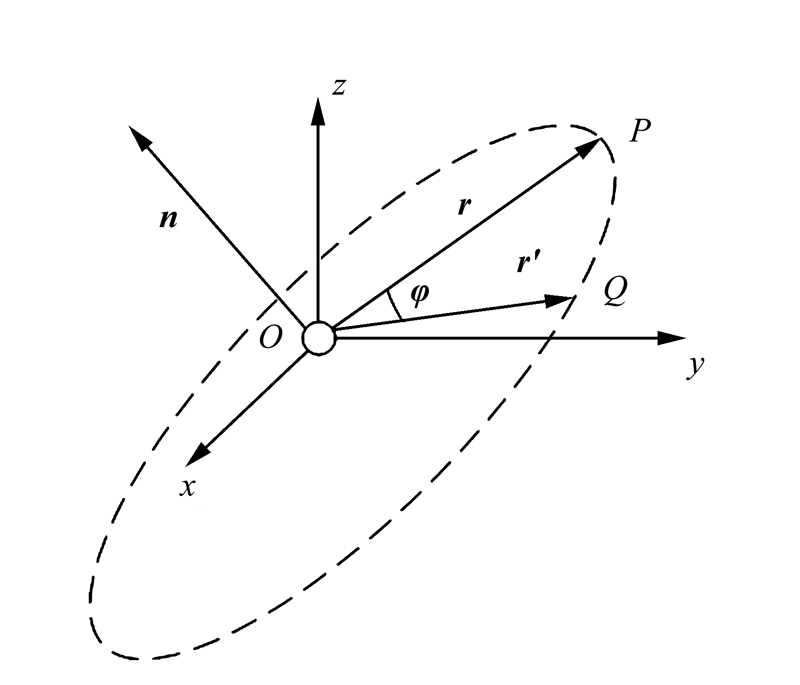 |
| 图 6 欧拉轴和旋转角示意图 Fig. 6 Euler axis and rotation Angle |
现在由欧拉轴和旋转角,求得其对应的四元数,设n=(n1,n2,n3),则四元数计算公式为
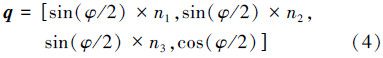
接下来由四元数求得欧拉角,设q=[x,y,z,w],欧拉角o=(α,β,γ),则欧拉角的计算公式为

计算旋转角的方法中有一步是预测关节在图像中的位置,其利用Xt-1=[xt-1,yt-1]T,Xt-2=[xt-2,yt-2]T即在t-1与t-2时刻的最优估计位置计算出Vt-1=[xt-1-xt-2,yt-1-yt-2]T关节在t-1时刻的速度,然后估计关节在t-1时刻的位置Xt=[xt,yt]T。可以发现,该算法做了关节的运行模式是速度不变的假设,而真实的跟踪过程中关节的运动模型是变速的且带有随机性的,会导致他们的局部寻优较慢,即迭代次数会变多;当预测位置出现较大偏差时,关节位置不在寻优区域导致找不到准确位置,会将错误的位置当做关节位置,进而影响算法后面的部分,导致错误的跟踪。因此,本文采用了粒子滤波的方式[13]对关节位置进行预测。
下面只对粒子滤波的自回归过程进行介绍,其他部分请参考文献[13]。自回归过程是一种通过历史数据来预测目前状态的时间序列建模策略。在这个模型里,目前的状态xt是一个依赖于以前状态的确定性函数并加上随机干扰,假如确定性函数是线性的,则目前的状态依赖于以前的 xp个状态,模型可以写成

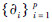 是自回归系数;ωt是随机干扰,一般情况下是白噪声。自回归系数既可通过学习的方法得到[15],也可以由特别的方式指定[16]。由于跟踪目标的连续性,采用变速模型更为适合一些,这里采用三阶自回归模型:
是自回归系数;ωt是随机干扰,一般情况下是白噪声。自回归系数既可通过学习的方法得到[15],也可以由特别的方式指定[16]。由于跟踪目标的连续性,采用变速模型更为适合一些,这里采用三阶自回归模型:
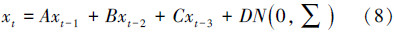
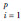 是自回归系数,N(0,∑)是零均值、标准方差为1的 Gaussian噪声。在试验中,指定系数为 A = 2,B = - 2,C = 3,D= 1。
是自回归系数,N(0,∑)是零均值、标准方差为1的 Gaussian噪声。在试验中,指定系数为 A = 2,B = - 2,C = 3,D= 1。
由上述计算过程可知,文中引入了变速模型和噪声,变速模型相对匀速模型能够更准确地表示关节的运动模型;引入噪声符合关节的运动具有随机性的特性,即关节有时会发生微小抖动。
因此,本文方法相对基于逆向运动学的方法能够更加准确地表示运动模型,进而能够更加有效的预测关节的位置,从而为后续的局部寻优,提供一个有效的预测,进而更加迅速和准确地找到最优估计,同时也会减少准确位置在寻优区域外部的概率,最终能够提高跟踪的速度和有效性。具体结果参见实验结果与分析部分。
3.3 实验准则的改进基于逆向运动学的实验准则,即通过手工标注的方式。手工标注的方式是通过人工标记获得实验图片序列中运动目标关节的二维图像位置,通过这种方式获取的关节位置具有主观性,因此获得的关节位置只能近似为真实的关节位置。
基于手工标注的主观性,提出了模拟仿真的方式。模拟仿真的方式是通过某种方式根据运动目标的关节位置,生成相应的图片序列并将其作为测试视频。此种方式获得的真实关节位置是相当可靠和准确的。具体方法是测试图像序列由3DMax软件生成,3DMax可以记录图像序列中的每个目标关节点的位置,包括空间三维坐标位置和二维图像坐标位置。然后,通过运动跟踪算法获得运动目标估计的图像关节位置。最后,将运动跟踪算法获得的关节二维图像坐标与3DMax中的关节二维图像坐标值进行比较。
由于实验条件与实验环境的限制,没有采用激光扫描仪等精准测量位置的工具。从而,不能通过激光扫描仪来获得运动对象的真实位置作为比较的基准。但是,可以用计算机图形学和运动合成技术来间接获得运动目标的关节位置的真实值。因此,在给定人体运动关节位置的情况下绘制了人体图像,然后对绘制的人体图像进行人体运动跟踪,最后将通过运动跟踪算法获得的估计值与真实值进行比较以验证跟踪算法的精确性。
这种间接获得目标真实数据的方式不仅成本低廉,而且比通过激光扫描仪获得的数据更精确、更可靠,也更简单。模拟仿真方式能够比手工标注方式获得更准确的关节真实坐标,而且相对于通过激光扫描仪等工具,具有更准确、更可靠、也更简单的优势,因此,此实验准则相对于基于逆向运动学的实验准则,有明显的优势,衡量实验结果也更加客观。
4 实验与分析 4.1 实验数据与评价准则本文算法在VS2008上实现,电脑配置为Intel(R) Core(TM)2,E7300,2.66 GHz,内存2 GB。此方法有效性的测试方式如下:
1)根据实验实际的人体运动视频来证明此方法的可行性。
2)将此算法与传统算法做对比,以此来定量说明本文算法的有效性。
本文测试视频为用松下HDC-HS20DV在普通室内光照下获得的视频。视频数据信息如图 2所示。
图 6~8为一部分实验结果,实验结果显示了人体骨骼结构的运动,从所有帧中每10幅图像取出一幅图像。评价准则采用实验获得的关节位置与手动获得的实际位置的像素级偏移;同时与比例正交投影算法、普通逆向运动学算法的像素误差进行比较。
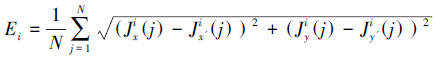
.jpg) |
| 图 6 1~40帧源视频与仿真效果图 Fig. 6 1~40 frame renderings of source video and simulation |
 |
| 图 7 61~100帧源视频与仿真效果图 Fig. 7 61~100 frame renderings of source video and simulation |
 |
| 图 8 120~160帧源视频与仿真效果图 Fig. 8 120~160 frame renderings of source video and simulation |
 |
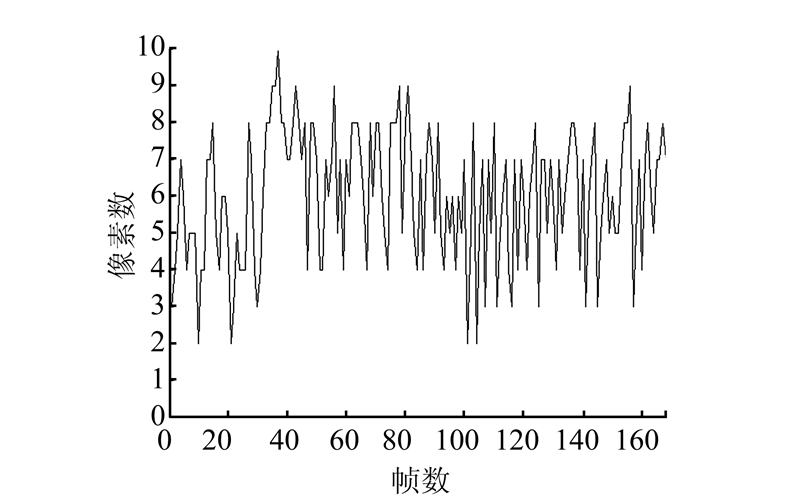
| 图 9 关节J7跟踪结果与手工标注关节位置的误差 Fig. 9 Tracking results with manually labeled J7 joint position |
 |
| 图 10 关节J12跟踪结果与手工标注关节位置的误差 Fig. 10 Tracking results with manually labeled J12 joint position |
由于实验条件所限,没有激光扫描仪来获得真实值作为比较的基准,但是可以用计算机图形学的技术来间接获得真实值,即在给定人体运动值下绘制人体图像,然后对绘制的人体图像进行人体运动跟踪,最后将估计出来的运动值与真实值进行比较。测试图像序列由3dmax软件生成,将本文算法获得的二维图像坐标与3dmax中的二维图像坐标值进行比较。实验效果图如图 11~13所示。
 |
| 图 11 1~40帧3dmax动画视频与仿真效果图 Fig. 11 1~40 frame renderings of 3dmax animation video and simulation |
 |
| 图 12 41~80帧3dmax动画视频与仿真效果图 Fig. 12 41~80 frame renderings of 3dmax animation video and simulation |
 |
| 图 13 81~120帧3dmax动画视频与仿真效果图 Fig. 13 81~120 frame renderings of 3dmax animation video and simulation |
由图 6~8可以看出,恢复出的每帧三维人体运动姿态与准确的人体运动姿态之间,误差还是存在的,然而实验恢复的人体运动姿态也还比较准确。实验恢复的误差很大成分是因为环境改变引起的,而且与根关节具有较大的偏离的关节恢复的偏差较大,例如,右腕的恢复偏差要比右肘的恢复偏差大。分析原因。因为子关节的恢复是以父关节的恢复为基础的,所以父关节恢复偏差影响它的所有的子关节的恢复。
基于定量偏差的计算的需求,计算了实验的关节的位置与手动获取的相对准确关节位置之间的偏差。其中,右肩位置J7、右膝位置J11的图像计算偏差分别是图 9~10。依照图 9~10,偏差相对较小,一般在10之内。环境的改变使得一部分图像会出现偏离准确值的情况,而前一图像的偏离不影响后面的计算,因此跟踪偏差只对当前帧有影响,故此方法有自修复的能力。表 1给出了本文跟踪算法的像素误差在测试视频中与比例正交投影和逆向运动学的比较结果;表 2给出了本文跟踪算法与比例正交投影、逆向运动学方法与由计算机图形绘制技术间接得到的真实值的像素误差。由表 2分析得,本文算法的像素误差基本在10像素以内,相对其他几种算法有较好的结果。因此,本文算法的有效性得到有力的证明。
| 关节 | 平均像素值误差 | ||
| 比例正交投影 | 逆向运动学 | 本文算法 | |
| 右肘 | 14.373 4 | 10.465 9 | 7.234 5 |
| 右腕 | 15.674 3 | 12.349 8 | 8.453 2 |
| 右膝 | 14.786 4 | 12.545 5 | 5.454 5 |
| 右踝 | 15.435 5 | 11.543 3 | 6.906 5 |
| 左肘 | 13.345 6 | 9.455 6 | 7.342 4 |
| 左腕 | 14.343 4 | 11.479 0 | 8.324 2 |
| 左膝 | 13.976 4 | 11.235 5 | 5.897 4 |
| 左踝 | 15.896 0 | 12.435 9 | 7.324 3 |
| 关节 | 平均像素值误差 | ||
| 比例正交投影 | 逆向运动学 | 本文算法 | |
| 右肘 | 16.148 2 | 11.970 1 | 9.047 9 |
| 右腕 | 17.319 0 | 13.824 1 | 10.617 9 |
| 右膝 | 16.290 2 | 14.254 2 | 9.271 4 |
| 右踝 | 17.259 0 | 13.016 4 | 8.638 1 |
| 左肘 | 15.589 1 | 10.938 1 | 9.581 0 |
| 左腕 | 16.288 1 | 13.782 4 | 10.637 1 |
| 左膝 | 16.003 4 | 13.027 8 | 7.362 9 |
| 左踝 | 17.648 3 | 14.368 1 | 9.558 1 |
本文在综合考虑跟踪效果和计算效率的情况下,提出了一种简单高效,且不牺牲跟踪结果质量的基于棍状模型的高效方法。此运动跟踪流程根据摄像机拍摄图像的流程更新形变外观模型,全部跟踪方法是由图像局部坐标映射相机立体空间坐标,之后反映射到图像局部坐标的方式。因此,为虚拟动画、基于视频的人机交互提供了一种新的方法。
| [1] | 阮涛涛, 姚明海, 瞿心昱, 等. 基于视觉的人体运动分析综述[J]. 计算机系统应用, 2010, 20(2): 245-253. RUAN Taotao, YAO Minghai, QU Xinyu, et al. A survey of vision-based human motion analysis[J]. Computer Systems & Applications, 2010, 20(2): 245-253. |
| [2] | 李豪杰, 林守勋, 张勇东. 基于视频的人体运动捕捉综述[J]. 计算机辅助设计与图形学学报, 2006, 18(11): 1645-1650. LI Haojie, LIN Shouxun, ZHANG Yongdong. A survey of video based human motion capture[J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(11): 1645-1650. |
| [3] | 龚文凌, 王洪澄, 孙敏. 视频交通监控系统中运动车辆捕捉算法的研究[J]. 微型机与应用, 2004, 23(3): 45-46. GONG Wenling, WANG Hongcheng, SUN Min. The research of motorial vehicle capture arithmetic on vision-based traffic monitor system[J]. Microcomputer & Its Applications, 2004, 23(3): 45-46. |
| [4] | 万成凯. 无标记人体运动捕捉及姿态估计的研究[D]. 北京: 北京交通大学, 2009: 2-10. WAN Chengkai. Research on marker-less human body motion capture and pose estimation[D]. Beijing: Beijing Jiaotong University, 2009: 2-10. |
| [5] | MULTON F, KULPA R, HOYET L, et al. Interactive animation of virtual humans based on motion capture data[J]. Computer Animation and Virtual Worlds, 2009, 20(5/6): 491-500. |
| [6] | 伍星. 基于第二代Bandelet变换的人体检测方法研究[D]. 西安: 西安电子科技大学, 2010: 5-10. WU Xing. Research on method in human detection based on second generation Bandelet transform[D]. Xi'an: Xidian University, 2010: 5-10. |
| [7] | GAVRILA D M. The visual analysis of human movement: a survey[J]. Computer Vision and Image Understanding, 1999, 73(1): 82-98. |
| [8] | JIANG Zhuolin, LIN Zhe, DAVIS L S. Recognizing human actions by learning and matching shape-motion prototype trees[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(3): 533-547. |
| [9] | ELGAMMAL A, SHET V, YACOOB Y, et al. Learning dynamics for exemplar-based gesture recognition[C] //2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Madison, WI, USA: IEEE, 2003, 1:571-578. |
| [10] | AN K H, CHUNG M J. 3D head tracking and pose-robust 2D texture map-based face recognition using a simple ellipsoid model[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems, 2008. Nice: IEEE, 2008: 307-312. |
| [11] | MORI G, MALIK J. Recovering 3D human body configurations using shape contexts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(7): 1052-1062. |
| [12] | 苟靖翔. 基于视觉信息特征和机器学习的人体运动跟踪与三维姿势恢复[D]. 西安: 西安电子科技大学, 2012: 10-12. GOU Jingxiang. Human pose estimation and 3D recovery based on visual geometric features and machine learning[D]. Xi'an: Xidian University, 2012: 10-12. |
| [13] | 刘琼, 彭光正, 刘昊. 基于粒子滤波算法的三维关节型人体运动跟踪[J]. 北京理工大学学报, 2011, 31(2): 163-167. LIU Qiong, PENG Guangzheng, LIU Hao. 3D articulated human body tracking by particle filter[J]. Journal of Beijing Institute of Technology, 2011, 31(2): 163-167. |
| [14] | 邹北骥, 陈姝. 适用于单目视频的无标记三维人体运动跟踪[J]. 计算机辅助设计与图形学学报, 2008, 20(8): 1047-1055. ZOU Beiji, CHEN Shu. Markerless 3D human motion tracking for monocular video sequences[J]. Journal of Computer-Aided Design & Computer Graphics, 2008, 20(8): 1047-1055. |
| [15] | 蔡杰, 郑江滨. 双目视觉下三维人体运动跟踪算法[J]. 计算机应用研究, 2009, 26(4): 1279-1281.CAI Jie, ZHENG Jiangbin. 3D human motion tracking algorithm in binocular camera system[J]. Application Research of Computers, 2009, 26(4): 1279-1281. |
| [16] | 陶霖密, 于亚鹏. 摄像机几何约束及人体定位[J]. 中国图象图形学报, 2012, 17(9): 1150-1157. TAO Linmi, YU Yapeng. Geometric constraints of locating cameras and people[J]. Journal of Image and Graphics, 2012, 17(9): 1150-1157. |
| [17] | 陈坚, 吴恩华. 单目视频中人体三维运动的迭代优化估计[J]. 计算机辅助设计与图形学学报, 2005, 17(7): 1523-1528. CHEN Jian, WU Enhua. 3D human motion reconstruction from monocular videos through iterative optimization[J]. Journal of Computer-Aided Design & Computer Graphics, 2005, 17(7): 1523-1528. |
| [18] | 马颂德, 张正友. 计算机视觉——计算机理论与算法基础[M]. 北京: 科学出版社, 1998: 52. |



