2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
悬垂绝缘子检测机器人是一类辅助人工在高空、高压的复杂电磁环境中对架空输电线路悬垂绝缘子串中低值和零值绝缘子[1, 2]进行检测的机器人,其解决了人工登塔检测效率低、安全性难保证、无法获得定量数据等问题[3],具有重要的研究价值和应用前景。
近年来,国内外出现了多种悬垂绝缘子检测机器人,按行走机构的原理主要分为蠕动式、履带式和轮腿式3类。蠕动式行走机构利用仿生学的原理沿悬垂绝缘子串爬行,如韩国电力研究院研制的悬垂绝缘子清扫机器人[4]和美国电力研究院的Ike机器人[5],这种机构运动稳定可靠,但是其步态控制复杂;意大利学者Luigi Paris[6]研发的高压绝缘子维护清扫机构采用了履带式的行走机构,其行走方式主要依靠履带沿绝缘子表面进行滚动式爬行,这种机构承载能力强、有很强的表面适应能力,广泛应用于各类越障机器人中,但其结构复杂、体积笨重;轮腿式行走机构是一种利用多组轮腿交替与绝缘子瓷裙接触以实现沿悬垂绝缘子串运动的机构,韩国电力研究院研制的绝缘子检测机器人[7, 8]和中国东北大学研制的叶轮滚动式悬垂绝缘子检测机器人[9]均是采用轮腿式行走机构,这种机构原理简单、运动连续、体积轻便,然而这类机构在对不同绝缘子串的适应性、运动稳定性及承载能力等方面略显不足。目前,国内外研制的悬垂绝缘子检测机器人处于功能实现阶段,具备行走和检测的基本功能。然而,实际线路中悬垂绝缘子串相邻绝缘子的轴线并不重合,绝缘子串本身存在小角度的弯曲,当前研制的悬垂绝缘子检测机器人设计时假设所有绝缘子的轴线重合,难以应用于实际线路环境。
针对上述绝缘子检测机器人行走机构存在的问题,本文提出了一种串并联复合式绝缘子检测机器人机构,该机构由蠕动式行走机构与检测机构组成,采用反平行四边形机构实现夹紧,利用Delta型并联机构实现三维移动,与现有的绝缘子检测机器人机构相比,该机构具有运动平稳、适应性好及负载能力强等特点。
1 环境描述与检测任务盘形悬式绝缘子是架空输电线路中常见的绝缘器件,按照DL/T 626-2005《劣化盘形悬式绝缘子检测规程》的要求,需定期执行测量分布电压、测量绝缘电阻和工频耐压实验中的一项检测。
在设计悬垂绝缘子检测机器人机构时,通常仅考虑绝缘子串处于铅垂状态的情况,即所有绝缘子片的轴线在同一直线上,如图 1(a)所示。实际上由于相邻绝缘子片依靠铁帽和钢脚连接,如图 1(b)所示,仅仅限制其高度方面的参数和位移,并未限制其相对转动[10],根据GB/T 4056-2008《绝缘子串元件的球窝连接尺寸》[11],相邻绝缘子片间临界夹角按不同联接标记规定为9°~12°,所以在实际线路中由于自然弯曲、安装误差、风载等原因,绝缘子串轴线有时呈现为一段小角度范围内弯曲的空间曲线,如图 1(c)所示。目前国内最常用的检测输电线路瓷质绝缘子的方法为人工登塔带电检测,即电力操作人员登上铁塔后,利用携带的绝缘杆将绝缘子检测装置靠近绝缘子,并使绝缘子检测装置的探针与相邻两绝缘子的铁帽可靠接触,测量绝缘子的绝缘电阻,根据绝缘电阻的大小判断低值绝缘子。图 1(a)所示为电力操作人员检测耐张瓷质绝缘子串。
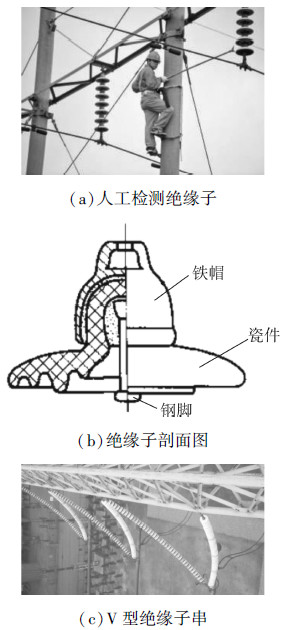 |
| 图 1 盘形悬式绝缘子串 Fig. 1 Cap and pin insulator strings |
基于上述环境描述与任务需求,借鉴人在爬树过程中的运动机理,提出机构方案。如图 2所示,通常人在爬树时双手双脚分别环抱夹紧树干,配合腰部的伸缩沿弯曲的树干爬行。本文依据人爬树的运动机理,在蠕动式和腿足式绝缘子检测机器人研究的基础上,提出了一种新型的串并联复合式悬垂绝缘子检测机器人机构。
 |
| 图 2 爬树过程示意 Fig. 2 Schematic of a child climbing a tree |
如图 3所示,机器人机构由推进机构、夹紧机构和检测机构组成。其中推进机构采用Delta型并联机构,包括上平台1、下平台2、上连杆组3、下连杆组4;夹紧机构包括上夹爪5、下夹爪6;检测机构包括探针7和旋转关节J6。
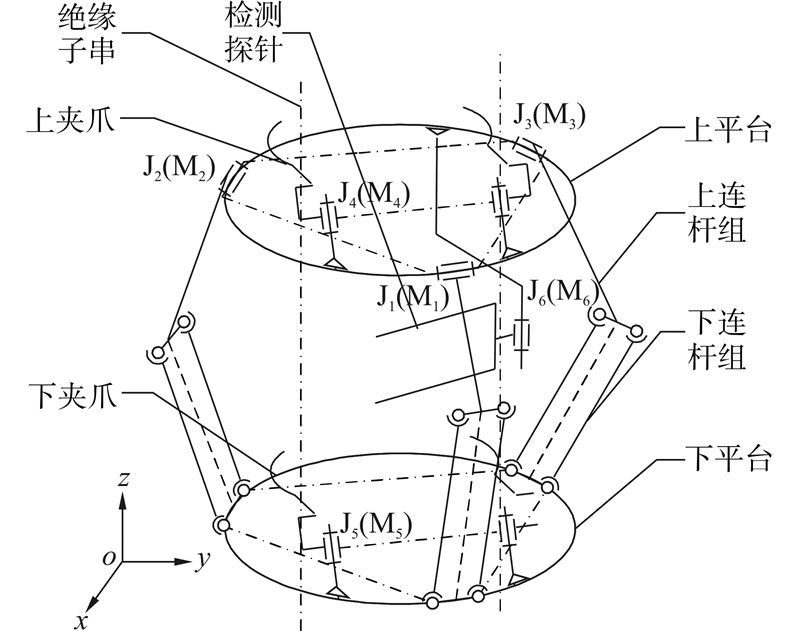 |
| 图 3 机构的构型 Fig. 3 Configuration of mechanism |
上连杆组由3个周向均布的连杆构成,每个连杆通过水平放置的旋转关节J1、J2、J3与圆环状上平台1连接,每个连杆分别通过电机M1、M2和M3驱动旋转关节实现上连杆绕上平台的旋转。下连杆组由6个周向均布的连杆组成,每个连杆采用球铰链与上连杆组3及圆环状下平台2连接。
上夹爪5采用反平行四边形夹紧机构,通过电机M4驱动垂直放置的旋转关节J4实现对绝缘子铁帽的夹紧。上夹爪5与下夹爪6结构相同,分别安装于机器人的上平台1和下平台2。
检测机构包括探针(与绝缘子检测仪相连接)、电机和齿轮组,其中探针7通过垂直放置的旋转关节J6与上平台1固连,通过电机M6驱动旋转关节实现探针对相邻两片绝缘子铁帽的搭接,通过绝缘子检测仪实现对绝缘子的零值及低值的检测。
2.2 Delta型并联机构Delta型并联机构具有3个平动自由度[12]。3条支链中的上连杆组3为驱动杆,与上连杆3铰接的下连杆组4为从动杆。当其中一个平台固定时,电机M1、M2和M3驱动上连杆组3,带动下连杆组4实现另外一个平台在X向、Y向和Z向的平移。其中Z向移动实现了机器人沿悬垂绝缘子串的爬行,由于悬垂绝缘子串属于柔性连接,平台在X向和Y向的平移可适应弯曲的绝缘子串。
2.3 夹紧机构夹紧机构包括上夹爪5和下夹爪6,两者结构相同,均采用反平行四边形机构。如图 4所示,机架AC与平台固连,长度为d,驱动连杆AB与左夹爪固连,长度为a,连杆BD长度为b,从动杆CD与右夹爪固连,长度为c,其中AB= CD,AC= BD。当电机M4驱动垂直放置的旋转关节J4,可实现夹爪的夹紧和松开。
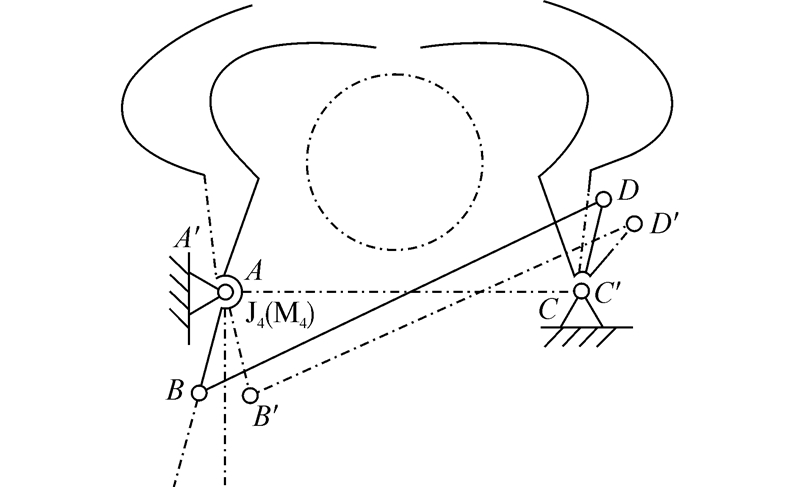 |
| 图 4 反平行四边形机构 Fig. 4 Anti-parallelogram mechanism |
探针、电机和齿轮组构成的检测机构如图 5所示。
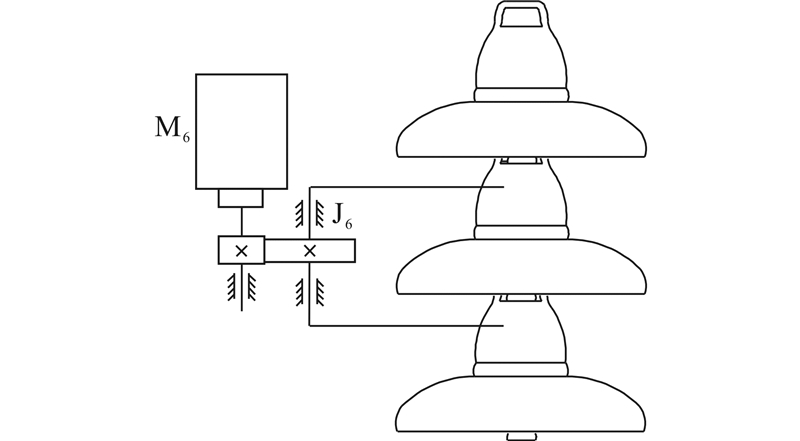 |
| 图 5 检测机构示意图 Fig. 5 Diagrammatic sketch of detection mechanism |
当机器人本体到达指定位置,通过电机M6驱动旋转关节J6,实现检测探针搭接在相邻两片绝缘子片的铁帽上,检测仪自动完成对绝缘子片绝缘电阻值的检测。
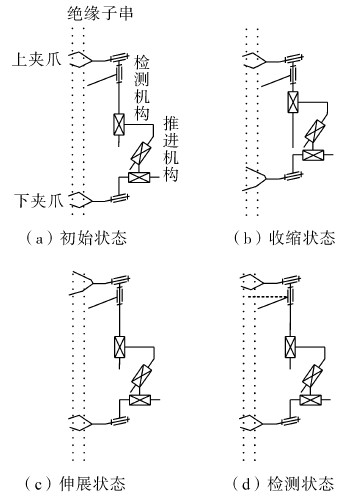
2.5 机构工作原理为便于介绍工作原理,给出该机器人机构的等效机构,如图 6所示,包括推进机构、检测机构、上夹爪和下夹爪。机构沿绝缘子串的运动采用蠕动式爬行,通过上下夹爪的交替夹紧和推进机构的伸缩,实现机器人沿绝缘子串的移动,移动过程中对绝缘子进行检测,等效机构对一片绝缘子的爬行及检测过程如下:
 |
| 图 6 运动过程示意 Fig. 6 Movement diagram of peristaltic mechanism |
1)初始状态:上夹爪和下夹爪同时夹紧铁帽,检测机构保持原位,见图 6(a);
2)收缩状态:上夹爪夹紧铁帽,下夹爪松开铁帽,推进机构收缩到图 6(b)所示的状态;
3)伸展状态:下夹爪夹紧铁帽,上夹爪松开铁帽,推进机构展开到图 6(c)所示的状态;
4)检测状态:绝缘子检测仪触发,检测机构对绝缘子阻值检测,检测结束后检测机构回到初始位置,完成一片绝缘子的检测,见图 6(d)。
3 运动分析与机构尺寸设计考虑到悬垂绝缘子检测机器人向上移动的过程中,机构的收缩与伸展运动过程是类似的,这里仅对机构收缩的运动过程进行分析。
3.1 推进机构运动学正反解考虑上平台固定、下平台运动的情况,建立图 7所示的坐标系。
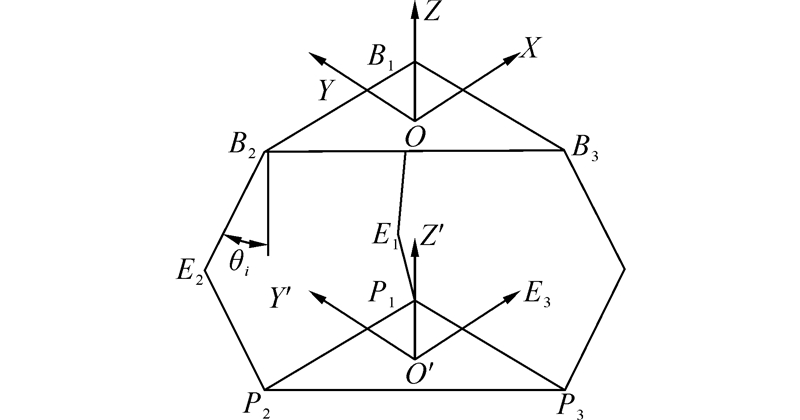 |
| 图 7 并联机构简化模型 Fig. 7 Simplified model of parallel mechanism |
该机构的运动学反解即给定下平台中心点在静坐标系中的坐标[O′]Ox,y,z即向量OO′,求解上连杆与上平台之间的张角θi的过程。根据支链的几何关系,得到
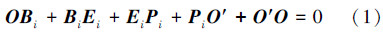

该机构的运动学正解是给定3个驱动关节J1、J2、J3的转角θ1、θ2、θ3,求解向量OO′的过程,本文构造如图 8所示的特征四面体OE1′E2′E3′[13],利用几何学及矢量代数的方法求解其运动学正解,其中F是其底面E1′E2′E3′的垂足,D为E1′E3′的中点,根据几何关系知道:
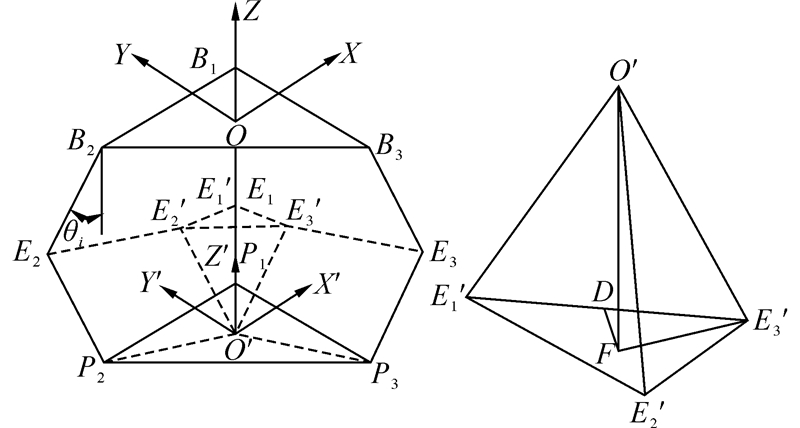 |
| 图 8 特征四面体 Fig. 8 Characteristic tetrahedron |
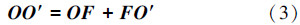
首先按文献[13]的方法首先求出OF:
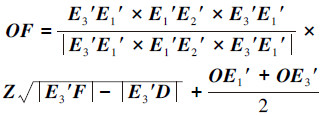
求解FO′,其结果如下所示:
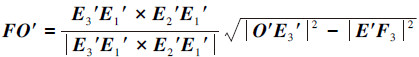
根据已知参数和上述几何关系得到OF、FO′,将其代入式(3)求得OO′的解析解,即该推进机构运动学正解。
3.2 机构尺寸设计图 9所示是一种常见的盘形瓷质双伞裙悬垂绝缘子XWP2-160,其主要结构尺寸公称盘径D为280 mm、公称结构高度H为155 mm。
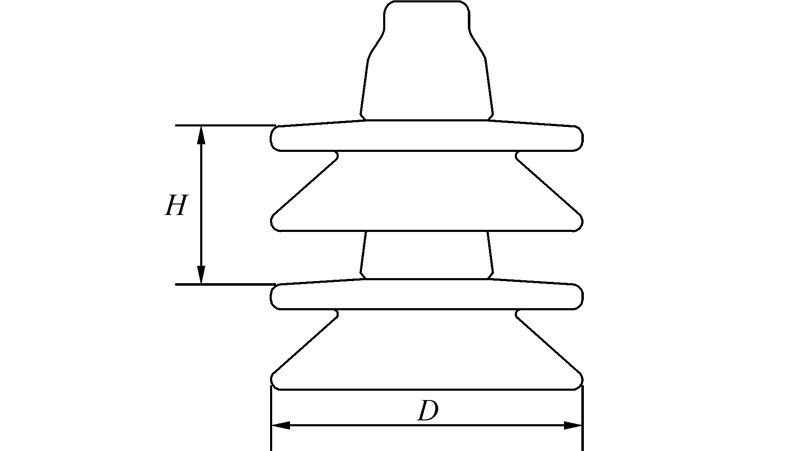 |
| 图 9 绝缘子参数 Fig. 9 Parameters of insulator |
结合该机构的原理与实际绝缘子的参数,初步选定本文中设计的机构各部分参数如表 1所示。
| 机构参数 | 数值/mm | 机构参数 | 数值/mm | |
| R | 180 | a | 30 | |
| r | 180 | b | 150 | |
| L b | 180 | c | 30 | |
| L a | 180 | d | 150 |
根据上面的分析和设计尺寸,在Solidworks中建立了机构的三维模型,如图 10所示。
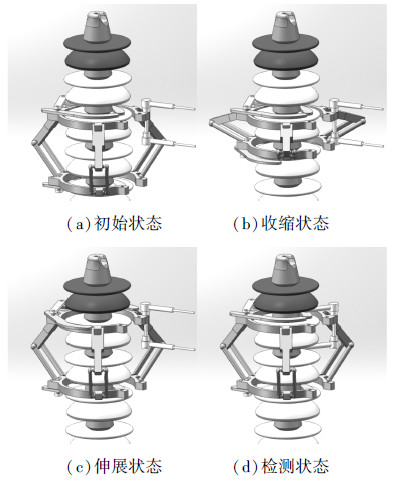 |
| 图 10 机构运动过程 Fig. 10 Movement process of mechanism |
机器人机构对绝缘子的检测功能在检测状态时由检测机构完成,机器人机构沿绝缘子串的爬行功能主要包括初始状态的收缩过程和从收缩状态到伸展状态的伸展过程,这2个过程是对称的,仿真针对机构的收缩过程进行。一般情况下,悬垂绝缘子串在重力作用下处于铅垂状态,任意2个相邻绝缘子片的轴线重合,绝缘子串轴线成一条直线,如图 11中绝缘子片1与绝缘子片2所示的情况,此时上平台固定在点G1附近,机构收缩过程中下平台从点G3直线移动到G2,只有Z方向上的运动,而X、Y方向上的位移均为0。
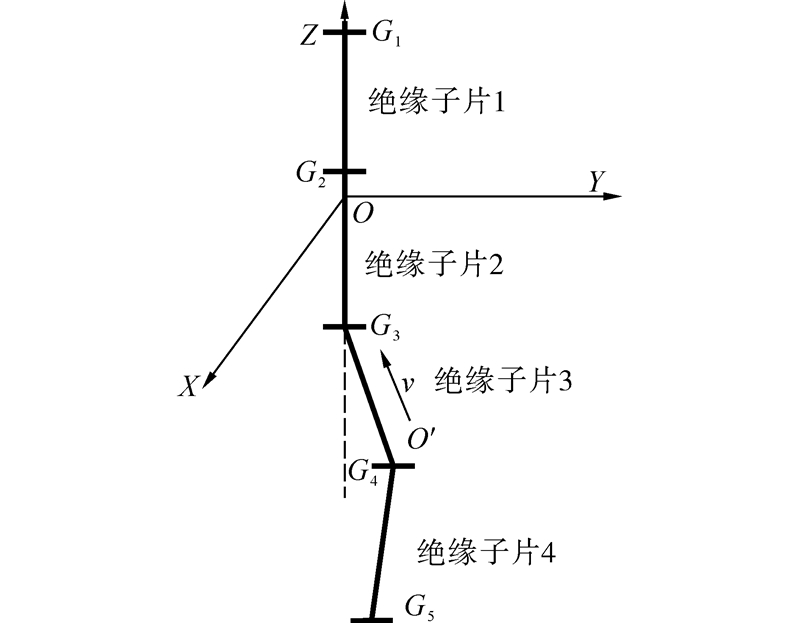 |
| 图 11 绝缘子串轴线 Fig. 11 Axis of insulator string |
然而,如前文所述,考虑到两片绝缘子之间属于柔性连接,由于自然弯曲、安装误差、风载扰动等原因,实际线路中的相邻绝缘子片轴线会出现不重合的情况,如图 11中绝缘子片2与绝缘子片3之间、绝缘子片3与绝缘子片4之间的情况所示。此时绝缘子串的轴线可近似表示成一条空间折线,收缩时上平台固定在点G2或G3附近,下平台从G5直线移动到G4或从G4直线移动到G3,这种情况下,需要X、Y、Z这3个方向的自由度。
给定机器人机构的收缩过程耗时5s,根据机构的爬行原理,收缩一次的行程为一个绝缘子的公称结构高度H,这里为155 mm,采用梯形规律规划其速度如图 12所示。
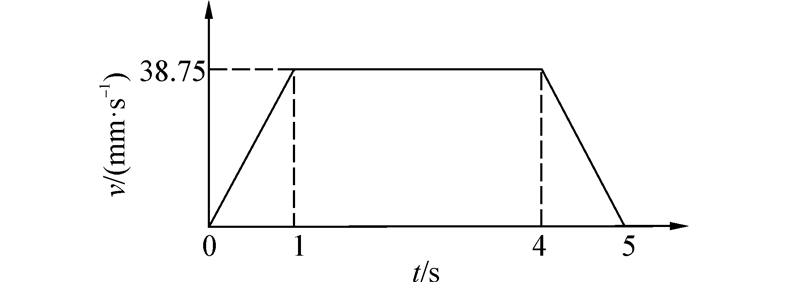 |
| 图 12 梯形速度规划 Fig. 12 Trapezoidal velocity planning |
仿真分析图 11中较复杂的情况,考虑到机构与绝缘子的实际尺寸,上平台固定在G2下方,收缩过程是下平台中心点O′按照图 12所规划的速度v从点G4直线运动到点G3的过程,以上平台中心点O为原点,点G3的坐标为(0,0,-125),点G4的坐标为(25.3,9.2,-277.6),可以计算出绝缘子片3的轴线相对绝缘子片2的轴线有10°的偏转。根据前述运动学反解的分析,在MATLAB中编程进行解算得到如图 13所示的结果。从结果可知,该机构的收缩过程利用推进部分3个驱动关节J1、J2、J3联动实现。
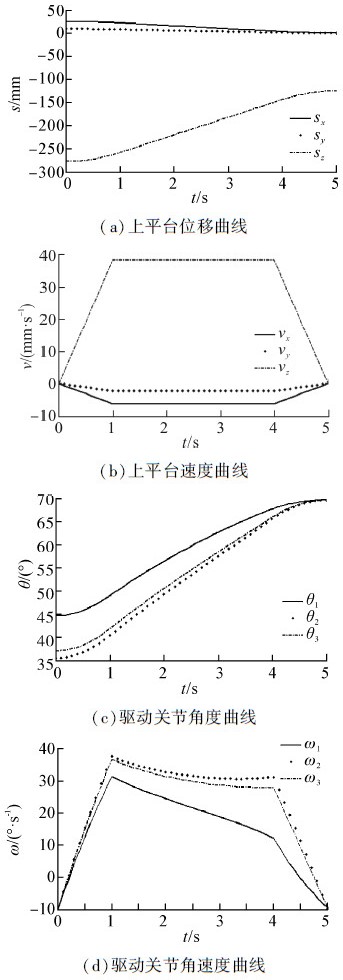 |
| 图 13 收缩运动曲线 Fig. 13 Curve of contraction movement |
为了验证其正确性,根据机构的运动学正解分析,在MATLAB中编程并从图 13(c)的结果中选取5组驱动关节J1、J2、J3的角度值代入进行解算,结果如表 2所示。
| 序号 | θ 1/(°) | θ 2/(°) | θ 3/(°) | x/mm | y/mm | z/mm |
| 1 | 44.7 | 35.4 | 37.0 | 25.3 | 9.2 | -277.6 |
| 2 | 55.7 | 48.4 | 49.7 | 16.4 | 6.0 | -224.2 |
| 3 | 62.1 | 56.7 | 57.6 | 10.1 | 3.7 | -186.1 |
| 4 | 67.3 | 64.7 | 65.2 | 3.8 | 1.4 | -147.9 |
| 5 | 69.7 | 69.7 | 69.7 | 0 | 0 | -125 |
从结果可知,表中序号为1的点与G4重合而序号为5的点与G3重合,经比较可知,二者间的数值完全一致。表中序号为2、3、4的点也可通过计算验证其均在以点G3和G4为端点的线段上。仿真结果表明该机构可以实现沿规划的空间直线收缩,机构伸展过程与此类似,配合夹爪的松开和夹紧,能够在一定范围内适应小角度弯曲的悬垂绝缘子串。
由以上仿真分析可知,机器人可以沿悬垂绝缘子串行走,并通过携带的检测装置对绝缘子进行零值和低值的检测。由于机器人机构采用并联机构原理设计,其负载能力较强,另外上平台和下平台具有沿X向、Y向和Z向运动的能力,机器人对悬垂绝缘子串的适应能力强,运动平稳可靠。
5 结束语面向输电线路悬垂绝缘子串检测任务的实际需求,本文提出了一种串并联复合式绝缘子检测机器人机构。分析与仿真结果表明,采用反平行四边形机构可实现有效的夹持,采用Delta型并联机构作为推进机构,不仅保证了移动过程中平稳可靠及负载能力强,而且能够在一定范围内适应小角度弯曲的悬垂绝缘子串。与现有的绝缘子检测机器人机构相比,本文提出的机构具有运动平稳、负载能力强及适应性好等优点,因而更具有实用价值。未来的工作主要包括控制系统设计、样机研制及实验研究。
| [1] | 国家电网公司. 110(66)kV-500kV架空输电线路管理规范[M]. 北京: 中国电力出版社, 2006: 1-171. |
| [2] | 武汉高压研究所.DL/T 626-2005, 劣化盘形悬式绝缘子检测规程[S]. 北京: 中国电力出版社, 2005. |
| [3] | 朱虎, 李卫国, 林冶. 绝缘子检测方法的现状与发展[J]. 电瓷避雷器, 2006(6): 13-17. ZHU Hu, LI Weiguo, LIN Ye. Present and future development of detection methods for composite insulator[J]. Insulators and Surge Arresters, 2006(6): 13-17. |
| [4] | PARK J Y, CHO B H, BYUN S H. Development of automatic cleaning robot for live-line insulators[C] //IEEE 11th International Conference on Transmission and Distribution Construction, Operation and Live-Line Maintenance.Albuquerque, USA, 2006: 1-7. |
| [5] | PHILLIPS A. Using robotics for insulators[J]. Electricity Today, 2014, 25(3): 76. |
| [6] | PARIS L. Equipment to carry out maintenanace operations, particularly washing, on insulator chains of high voltage electric lines[P]. United States: 5119851. 1992-06-09. |
| [7] | PARK J Y, LEE J K, CHO B H, et al. Development of inspection robot system for live-line suspension insulator strings in 345kV power transmission lines[C]// 13th European Conference on Power Electronics and Applications. Barcelona, Spain, 2009: 1-8. |
| [8] | PARK J Y, LEE J K, CHO B H, et al. Development of advanced insulator inspection robot for 345kV suspension insulator strings[C]s. //Proceedings of the International MultiConference of Engineers and Computer ScientistHong Kong, China, 2010: 1088-1109. |
| [9] | 赵治国. 悬垂绝缘子检测机器人机构设计与分析[D]. 沈阳: 东北大学, 2012: 1-67. ZHAO Zhiguo. Mechanism design and analysis of suspension insulator inspection robot[D]. Shenyang: Northeastern University, 2012: 1-67. |
| [10] | 邹祥艳. 输电线路悬垂绝缘子串风致失效机理及防治[D]. 南昌: 南昌航空大学, 2013: 1-71. ZOU Xiangyan. Mechanism and prevention of wind-induced failure of transmission line suspension insulator string[D]. Nanchang: Nanchang Hangkong University, 2013: 1-71. |
| [11] | 西安电磁研究所. GB/T 4056-2008, 绝缘子串元件的球窝连接尺寸[S]. 北京: 中国标准出版社, 2008. |
| [12] | 梁香宁, 牛志刚. 三自由度Delta并联机器人运动学分析及工作空间求解[J]. 太原理工大学学报, 2008, 39(1): 93-96. LIANG Xiangning, NIU Zhigang. Kinematic analysis and workspace of 3-Dof delta parallel robot[J]. Journal of Taiyuan University of Technology, 2008, 39(1): 93-96. |
| [13] | 赵杰, 朱延河, 蔡鹤皋. Delta型并联机器人运动学正解几何解法[J]. 哈尔滨工业大学学报, 2003, 35(1): 25-27. ZHAO Jie, ZHU Yanhe, CAI Hegao. Geometric solution for direct kinematics of delta parallel robot[J]. Journal of Harbin Institute of Technology, 2003, 35(1): 25-27. |



