2. 天津市智能机器人技术重点实验室, 天津 300071
2. Key Laboratory of Intelligent Robotics of Tianjin, Tianjin 300071, China
在实际工程应用中,由于单个智能体自身能力的局限性,在处理复杂任务或处于复杂环境下仅靠个体行为往往无法解决。人们受到自然界中鱼群、鸟群等生物种群协作完成捕食、迁移等生物集群协作行为的启发,将这种生物集群编队协作的特点运用到多智能体系统中[1, 2, 3]。近年来,多智能体编队协同控制吸引了越来越多的研究者。如今,随着研究的不断深入和发展,多智能体编队协同控制已经得到了广泛的应用,如环境勘探、残留有毒物清理、大型物体运输、搜寻与救援任务等[4, 5]。而多机器人编队控制是多智能体系统研究中最典型的问题之一。同时随着人工智能科学的不断发展,越来越多的人工智能算法被应用到多智能体系统中来,其中模糊控制是人工智能研究的热点之一。模糊控制本身属于一种非线性控制,它不依赖于被控对象的数学模型。对于模型中具有高度非线性和不确定性因素以及难以建立模型的被控对象,基于专家经验的模糊控制具有较强的优势[6]。模糊控制中的模糊逻辑是用人类的语言语句表达的,因此,它较为直观,易于人们理解[7]。无论是在科学研究还是工程实际运用上都逐渐被广泛应用[8, 9]。但在实际工程中模糊控制规则的制定没有统一的模式,往往需要丰富的工程实践经验,因此模糊控制器设计较为困难,且对设计人员的要求较高。同时大量的模糊规则使得存贮模糊规则库的计算机内存空间必须足够大,这对于如单片机等内存有限的硬件系统而言,显然无法满足其内存要求。因此模糊控制系统在可应用性、可移植性及扩展性上并不具备优势[10, 11]。
大多数基于领导-跟随方式的多机器人系统编队控制主要工作是设计协同控制律使得各个智能体达到并保持给定的期望队形,对于领导者自身的运动轨迹往往并不关心[12]。随着工程研究的广泛和深入,在利用多机器人执行编队任务(如多无人水下航行器水下地形测绘,多无人机编队协同打击等[13])时,若同时对领导者的运动轨迹加以限制,针对不同的地形环境对领导者的运动轨迹进行合理规划后使其沿给定轨迹运动,则可大大提高多机器人系统编队协同控制在实际应用中的效率及适应和应变能力。
许多学者做过关于编队控制和路径跟踪的研究,文献[1]讨论了离散时间下的多机器人编队控制,通过设计合理的控制律,使每个机器人的位姿信息与前一个机器人的位姿信息之差收敛到给定期望队形的编队向量来保证多智能体编队协同运动。文献[14]中提到SBC控制,通过对当前机器人的运动信息加以控制,使当前机器人与参考机器人的相对距离和角度总保持在给定值来完成编队。目前在路径跟踪研究中,已有一些学者利用智能控制方法成功解决路径跟踪问题,文献[15]采用预测控制方法对机器人进行运动控制,使其达到跟踪给定路径目的。文献[16]采用遗传控制算法,将机器人运动规划转化为非线性控制系统的优化问题,通过不断优化机器人的运动轨迹来完成路径跟踪目的。
针对轮式机器人模型高度非线性及运动学和动力学模型不易确定等特点,本文采用了不依赖于系统模型的模糊控制方法,通过不断调整机器人的控制输入来对每个子目标点实时跟踪,从而实现领导者沿整条期望轨迹运动。本文设计的模糊控制器控制规则简单明了,易于理解,且规则数较少,减少了对硬件的依赖,具有良好的可移植性和可扩展性。同时,通过对每个跟随者与领导者之间的相对距离l和角度φ加以控制,使其收敛到给定值,以此完成编队控制效果。
1 机器人模型对于作为领导者的移动机器人而言,其运动学模型只根据自身的位姿信息确定;而对于作为跟随者的移动机器人,其运动学模型建立在与领导者的位姿信息基础之上,通过与领导者的相对位置和角度信息来间接描述其自身的位姿信息。
1.1 领导者运动学模型设轮式移动机器人在某一运动时刻t的质心坐标点为M(x,y),此时机器人的速度方向与x轴正方向的夹角为θ,如图 1所示。机器人在这一时刻的位姿信息由向量q=(x,y,θ)T确定,机器人的运动信息由向量p=(v,w)T确定,其中v(t)和w(t)分别表示机器人在t时刻的线速度和角速度。
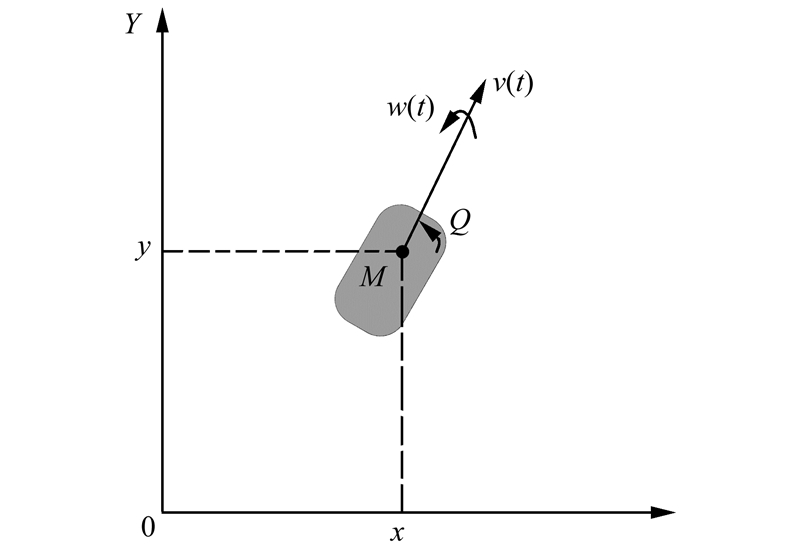 |
| 图 1 机器人运动学模型 Fig. 1 Kinematic model of the robot |
由图 1知,机器人的运动学方程可表示为
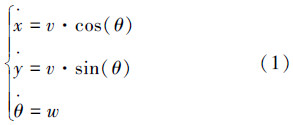
 =R(θ)p,其中
=R(θ)p,其中
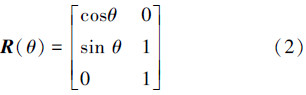
设2个机器人在t时刻的线速度分别为v1(t)和v2(t),它们的运动方向与x轴正方向的夹角为θ1和θ2。以机器人两轮轴心连线的中点为参考点,令机器人1为领导者,机器人2为跟随者,两机器人旋转点之间的距离为l,跟随机器人前进方向与两机器人旋转点连线的夹角为φ。如图 2所示。
 |
| 图 2 跟随者保持队形模型 Fig. 2 Formation keeping model of followers |
需要指出的是,由于当机器人原地旋转时参考点的线速度始终为零,为研究方便,选取以机器人的参考点为起点沿机器人前进正方向平移距离d得到的机器人的质点作为机器人的旋转点,以此来保证机器人运动过程中线速度始终非零。
令γ=θ2-θ1+φ,在对跟随者的运动状态进行数学描述时,文中采用SBC控制(separation-bearing control,SBC)方法建立跟随者模型[15]。因此对跟随者进行建模时,由跟随者与领导者的相对位置和角度表示的跟随者的运动学方程为
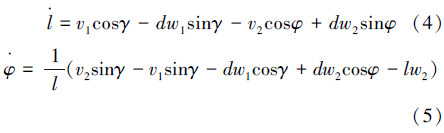
对领导者采用模糊控制方法,使其能够达到并沿着给定曲线运动。对跟随者,通过实时控制与领导者的相对距离和相对角度,使其同时收敛到给定值来达到编队控制的目的。
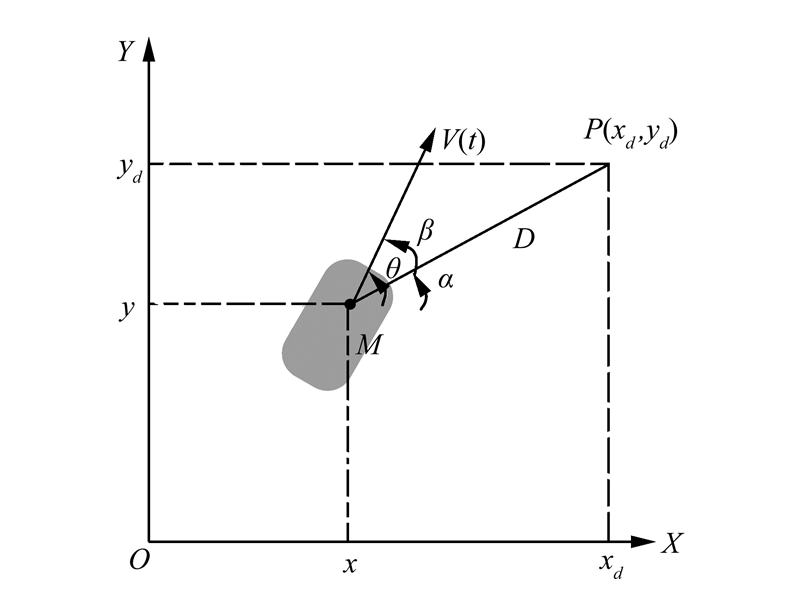
2.1 基于模糊控制的路径跟踪将给定曲线分解为若干个目标点,采用模糊控制方法使机器人总能到达距当前自身位置距离最近的目标点。如图 3所示,设当前所要到达的目标点为P(xd,yd),移动机器人的质点M与目标点P的距离为D,线速度方向水平夹角为θ。参考点与目标点连线的夹角为α。
 |
| 图 3 领导者向目标点移动 Fig. 3 The leader move to the target |
令β即为机器人运动方向与目标点的偏离角,则β=θ-α。选取D与β作为模糊控制器的输入量,机器人的线速度v(t)和角速度w(t)作为模糊控制器的输出量。通过设计合理的模糊控制规则,来保证移动机器人在轨迹跟踪的过程总能达到目标点P,即变量D与β总是趋于零,即可达到机器人实时跟踪给定轨迹的目的。下面由模糊语言变量分别对2个输入输出变量进行模糊子集的划分,如表 1和表 2所示。
| 距离D | 角度β |
| ZE 零 | NL 负大 |
| VN 非常近 | NM 负中 |
| NE 近 | NS 负小 |
| ME 中等 | ZE 零 |
| FA 远 | PS 正小 |
| VF 非常远 | PM 正中 |
| EF 格外远 | PL 正大 |
| 速度v | 角速度w |
| ZE 零 | NL 负大 |
| VS 非常小 | NM 负中 |
| SM 小 | NS 负小 |
| ME 中等 | ZE 零 |
| LA 大 | PS 正小 |
| VL 非常大 | PM 正中 |
| EL 极大 | PL 正大 |
对2个输入变量和输出变量的模糊集合均采取形式较为简单的三角形隶属度函数,简化了设计工作。在设计夹角β的隶属度函数时,考虑到轮式机器人的偏离角大多保持在[-90, 90]范围内这一实际情况,将属于这一区间的隶属度函数的模糊语言变量密度加大。同时对于偏离角较大的情况时,采用最大隶属度,使得机器人在实际运动中能够快速调整自身位姿信息,跟踪上给定的路径。选取三角形隶属度函数来限定这些语言变量的值如图 4~7所示。
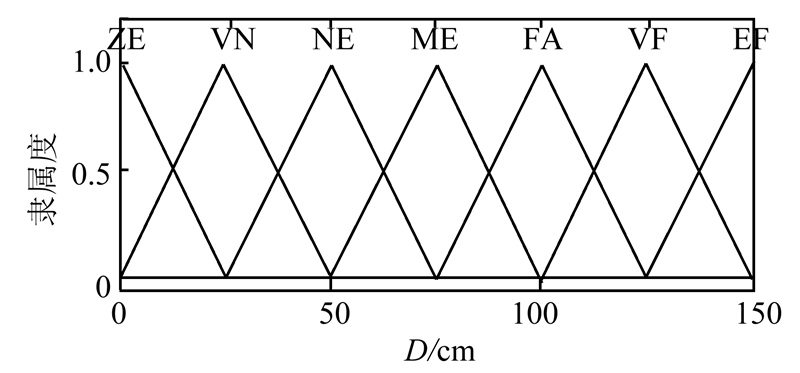 |
| 图 4 D隶属度函数 Fig. 4 subordinate degree function of D |
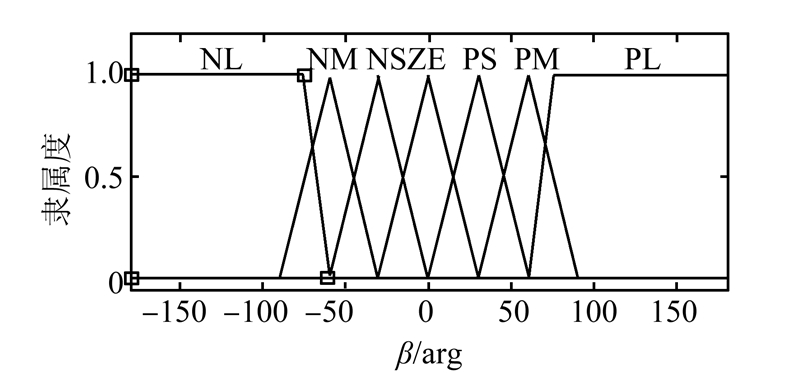 |
| 图 5 β隶属度函数 Fig. 5 subordinate degree function of β |
 |
| 图 6 v隶属度函数 Fig. 6 subordinate degree function of v |
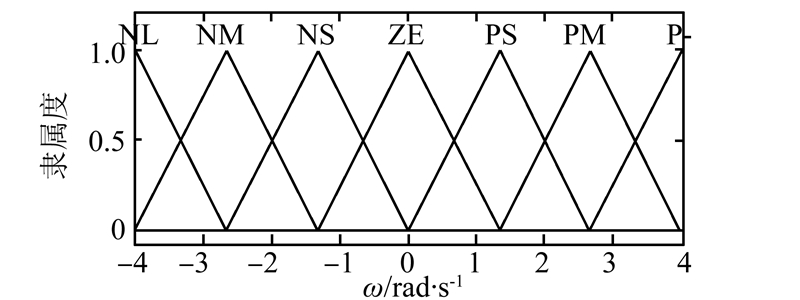 |
| 图 7 w隶属度函数 Fig. 7 subordinate degree function of w |
对于模糊规则的制定往往靠专家经验总结而来,它反映了从输入到输出的映射关系。本文对于模糊规则制定的核心思想是对机器人与目标点的距离D较大(或较小)时要求由模糊控制器输出一个较大(或较小)的线速度v(t);同时对机器人与目标点的偏离角β较大(或较小)时要求由模糊规则输出一个较大(或较小)的角速度w(t)。由此可以保证机器人始终在由一系列目标点构成的给定路径上运动。本文采用2个输入和输出变量、7个语言变量模糊集,对输出变量v(t)和w(t)分别进行模糊控制,两输出变量各自可以归纳出7条模糊规则。它们的模糊规则形式如下:
变量v(t)的模糊规则:

变量w(t)的模糊规则:

其中 i、
i、 i、
i、 i、
i、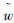 i(i=1,2,…,7)表示在表 1和表 2中4个输入输出变量在第i条规则下各自对应的语言变量值。
i(i=1,2,…,7)表示在表 1和表 2中4个输入输出变量在第i条规则下各自对应的语言变量值。
模糊推理方法又称去模糊化方法,常用的模糊推理算法有重心法(centroid)、面积平分法(bsector) 、平均最大隶属度法(mom) 、最大隶属度取最小值法(som)等。最常用的去模糊化方法是重心法。这里采用重心法计算第i条规则的输出:
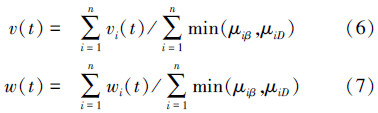
在路径跟踪控制中,利用Mamdani型这一基本的模糊逻辑系统对领导者运动轨迹加以控制。在设计模糊控制器的过程中,输入输出变量论域范围的选择至关重要。针对实验中的轮式机器人自身参数的约束,将线速度的取值限定在区间[0 m/s,1 m/s]范围内,同时结合实际场地实验情况及一定的容许度等因素,对角速度的取值限定在区间[-4 rad/s,4 rad/s] 范围内较为合理。对于规则库的制定采用单输入单输出(single-input single-output,SISO)形式的语言条件,制定方法简单直观,同时由于规则数较少,可有效节省存放规则表的内存空间,从而极大地减小了对硬件的要求,对于存储空间有限的移动机器人具有更强的可应用性。
2.2 跟随者编队保持在图 2所描述的对象模型中,令误差向量为[el,eφ]T=[ld-l,φd-φ]T。在编队运动过程,若能始终保持每个跟随者与领导者之间的相对距离l和角度φ均收敛到给定值(ld,φd),即满足
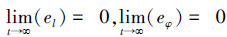
即可达到编队控制目标。
设计闭环控制律:
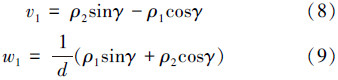

则有下面的结论。
定理1 对于任意给定参数满足α1、α2>0,若跟随机器人的控制律采用式(8)和(9),则有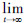 (el)=0和
(el)=0和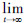 (eφ)=0同时成立,即多机器人系统可以实现稳定的编队。
(eφ)=0同时成立,即多机器人系统可以实现稳定的编队。
证明 构造李雅普诺夫函数V=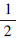 el2+
el2+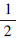 eφ2,对v求导
并代入运动学方程(4)和(5),得
eφ2,对v求导
并代入运动学方程(4)和(5),得
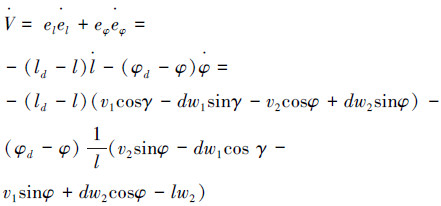
将控制律式(8)和(9)代入:
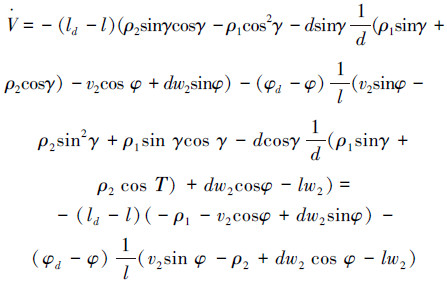
将式(10)、(11)代入并进一步整理可得
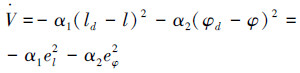
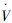 ≤0当且仅当el=0、eφ=0时等号成立。则系统渐近稳定。证毕。
≤0当且仅当el=0、eφ=0时等号成立。则系统渐近稳定。证毕。
该编队算法实现过程较为简便且思路清晰,易于接受。通过改变期望距离ld和角度φd的值,可以完成任意编队队形要求,具有较好的灵活性。由于在编队运动的过程中,所有跟随者都只与领导者进行通信,因此在编队运动过程中随时加入新的跟随者,不会对现有队形产生影响,且对跟随者的数量没有限制,体现该算法良好的扩展性。
同时也注意到,在计算跟随者的控制律时,其控制律高度依赖于领导者模型。在通信过程中由于噪声干扰或通信延迟等因素影响,一旦领导者的位姿信息不能准确地被跟随者获取时,跟随者便立即无法完成与领导者的编队协同控制。因此,这就要求领导者在通信传输方面具有较高的精度及较强的稳定性。
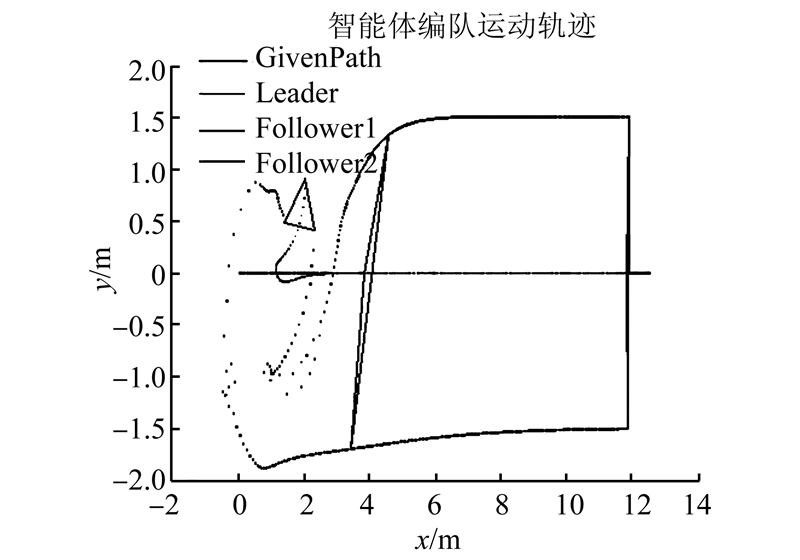
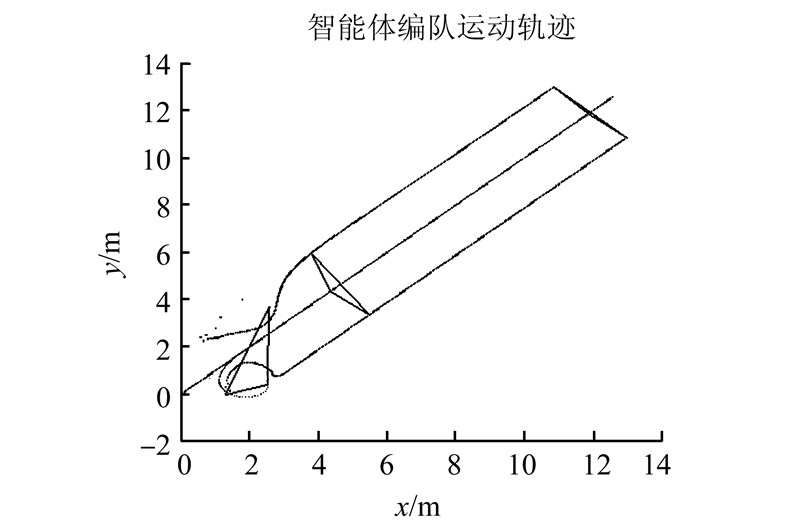
3 仿真研究 3.1 基于MATLAB的数值仿真为了验证该算法的有效性,采用MATLAB软件进行对多机器人系统进行数字仿真测试。领导者给定路径分别选取为直线y=0,y=x和圆x2+y2=4。领导者与跟随者初始位置信息随机给定。2个跟随者编队期望距离和角度(l,φ)分别为(1.5,90°),(1.5,-90°),即跟随者分别位于领导者的两侧并与领导者保持1.5 m的距离。
图 8~10为多机器人的运动轨迹。从图中可以看出,开始时每个智能体的起始位置随机分布,由编队控制算法对每个智能体加以控制。从图中可以看出经过一段时间后每个智能体均逐步达到了各自期望的位置并同时保持期望的队形运动。
 |
| 图 8 领导者给定路径为直线y=0时的编队运动轨迹 Fig. 8 Formation trajectory when the given path of leader is the straight line y=0 |
 |
| 图 9 领导者给定路径为斜线y=x时的编队运动轨迹 Fig. 9 Formation trajectory when the given path of leader is the diagonal line y=x |
 |
| 图 10 领导者给定路径为圆x2+y2=4时的编队运动轨迹 Fig. 10 Formation trajectory when the given path of leader is the circle x2+y2=4 |
为了进一步验证该编队控制算法的有效性,并从实际应用的角度出发,采用轮式移动机器人进行实际场地实验。
本实验采用的是美国ActivMedia Robotics公司生产的Amigo移动机器人作为实验平台。首先利用该公司提供的配套仿真软件MobileSim进行仿真测试,再利用Amigo机器人进行实际场地实验。主程序流程图如图 11。
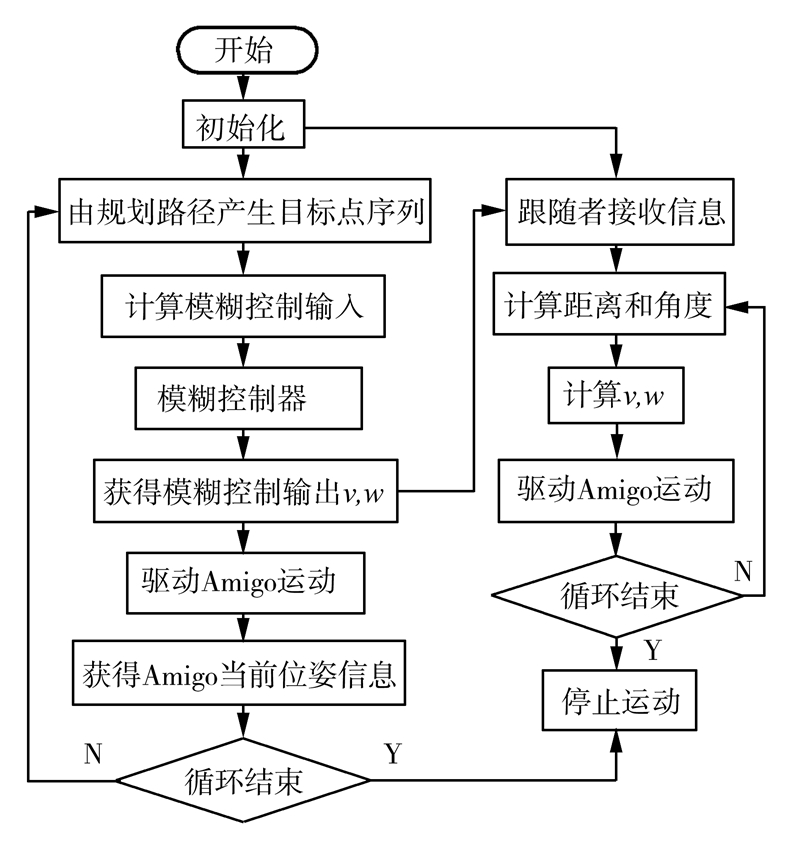 |
| 图 11 程序流程图 Fig. 11 The program flow chart |
本实验采用3个Amigo机器人分2组进行,第一组实验的领导者给定路径为直线y=2,2个跟随者与领导者的期望距离均为1 m,期望角度分别为90°和-90°,即分别位于领导者的左右两侧。第2组实验的领导者给定路径为圆x2+(y-5)2=25,两跟随者的期望距离均为1 m,期望角度分别为90°和0,即2个跟随者分别位于领导者的正前方和左侧。分别选取Amigo机器人在t1和t2这2个不同时刻的实际场地运动情况,如图 12、13所示。图 14、15是由移动机器人码盘采回的实际运动数据所绘制的运动轨迹图,并在图中分别给出几种不同时刻机器人的队形保持情况,如图中黑色实线所示。在图 14和图 15中标注的机器人在t1、t2时刻的编队运动情况分别与图 12和图 13中的t1、t2时刻一一对应。可以看出,在实际场地实验中,当给定轨迹为直线和圆时,采用该算法,领导者能够完成跟踪给定路径的要求,同时跟随者能够较快地达到并保持给定编队队形。由数字仿真和实际场地实验共同表明,该算法能够很好地完成所要求的控制目标,具有一定的有效性。
 |
| 图 12 领导者跟踪直线时的不同时刻t的编队运动情况 Fig. 12 The formation situation when the leader tracking the straight line in different time t |
 |
| 图 13 领导者跟踪圆时的不同时刻t的编队运动情况 Fig. 13 The formation situation when the leader tracking the circle in different time t |
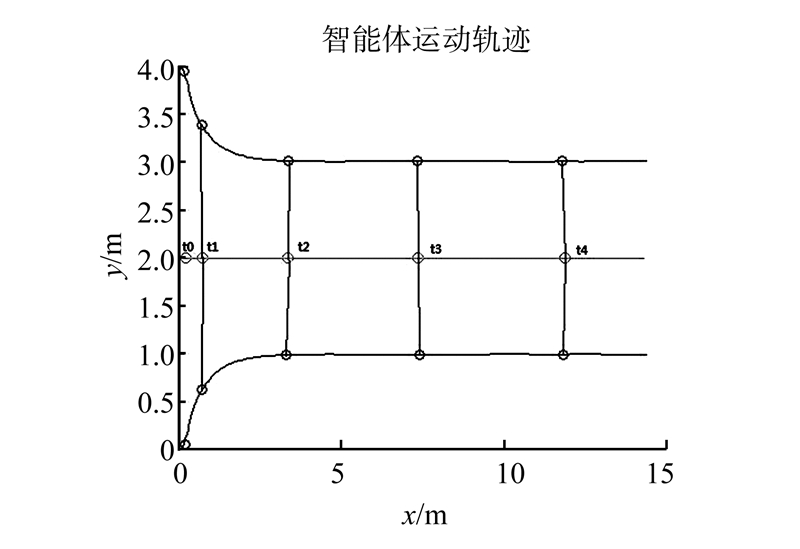 |
| 图 14 领导者跟踪直线时的实际输出的运动曲线 Fig. 14 The actual output curves when the leader tracking the straight line |
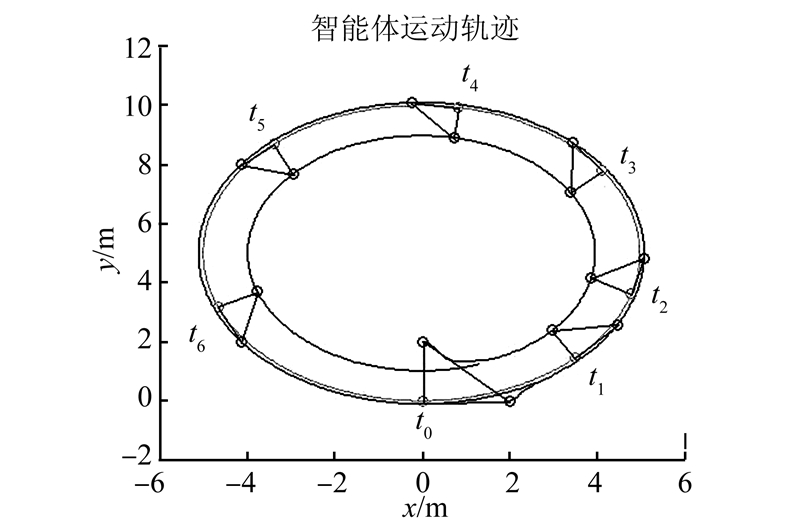 |
| 图 15 领导者跟踪圆时的实际输出的运动曲线 Fig. 15 The actual output curves when the leader tracking the circle |
本文运用Mamdani型模糊控制的方法对领导者运动轨迹加以控制,通过设计合理的模糊控制器,达到领导者沿给定轨迹运动的控制目标。模糊控制器的设计思想简单明了,规则的制定没有过度依赖专家经验,易于他人理解,且控制规则数较少,节省了一定的硬件资源。对跟随者设计控制律使其与领导者的相对位置和角度收敛到给定值,从而实现编队控制。通过数值仿真和移动机器人实验平台的测试进一步验证了该控制律的有效性。同时注意到模糊控制类型多种多样,例如不需要清晰化过程的T-S型模糊系统,形式上更加紧凑和易于计算的Sugeno型模糊系统等。也有很多结合人工智能领域其他算法的模糊控制,如基于神经网络的模糊控制,基于遗传算法的模糊控制等。这些模糊控制的方法同样可以应用到对领导者的路径跟踪系统中来。对于其他模糊控制方法的研究与应用将会在今后工作中进行。
| [1] | WANG F, GAO L X, WANG L Y. Tracking Control for Multi-agent Consensus for Discrete-time Case[C]//2011 Chinese Control and Decision Conference. Mianyang, China: IEEE, 2011: 923-928. |
| [2] | JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988-1001. |
| [3] | 苗国英, 马倩.多智能体系统的协调控制研究综述[J].南京信息工程大学学报: 自然科学版, 2013, 5(5): 385-369. MIAO Guoying, MA Qian.A survey of developments on coordinated control of multi-agent systems[J]. Journal of Nanjing University of Information Science and Technology: Natural Science Edition, 2013, 5(5): 385-369. |
| [4] | PENG Z X, WEN GG, RAHMANI A. Leader-follower formation control of multiple nonholonomic robots based on backstepping[C]//Proceedings of the 28th Annual ACM Symposium on Applied Computing. New York, NY, USA: SAC, 2013: 211-216. |
| [5] | HONG Y G, HU J P, GAO L X. Tracking control for multi-agent consensus with an active leader and variable topology[J]. Automatica, 2006, 42(7): 1177-1182. |
| [6] | HERNANDEZ-MENDOZA DE, PEÑ ALOZA-MENDOZA G R, ARANDA-BRICAIRE E. Discrete-Time Formation and Marching Control of Multi-Agent Robots Systems[C]//2011 8th International Conference on Electrical Engineering Computing Science and Automatic Control (CCE). Merida City: IEEE, 2011: 1-6. |
| [7] | ARAI T, PAGELLO E, PARKER L E. Guest editorial advances in multirobotsystems[J]. IEEE Transactions on Robotics and Automation, 2002, 18(5): 655-661. |
| [8] | 刘曙光, 魏俊民, 竺志超. 模糊控制技术[M]. 北京: 中国纺织出版社, 2001: 1-8. LIU Shuguang, WEI Junmin, ZHU Zhichao. Fuzzy control technology[M]. Beijing: China Textile Press, 2001: 1-8. |
| [9] | 孙德丰. MATLAB模糊系统设计[M].北京: 国防工业出版社, 2009.SUN DefengThe design of Fuzzy Systems[M]. Beijing: National Defence Industry Press, 2009. |
| [10] | HSU Y -C, CHEN G R, LI H X. A Fuzzy adaptive variable structure controller with application to robot manipulators[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2001, 31(3): 331-340. |
| [11] | 骆德渊, 刘荣, 李纪文. 采用模糊逻辑的移动机器人轨迹跟踪[J].电子科技大学学报, 2008, 37(6): 943-947. LUO Deyuan, LIU Rong, LI Jiwen. Path tracking of mobile robots using fuzzy logic[J].Journal of University of Electronic Science and Technology of China, 2008, 37(6): 943-947. |
| [12] | 陈杨杨, 田玉平.多智能体沿多条给定路径编队运动的有向协同控制[J].自动化学报, 2009, 35(12): 1541-1549.CHEN Yangyang, TIAN Yuping. Directed coordinated control for multi-agent formation motion on a set of given curves[J]. ActaAutomaticaSinica, 2009, 37(12): 1541-1549. |
| [13] | 徐国焯.多UUV编队路径跟踪控制研究[D].哈尔滨:哈尔滨工程大学, 2012:12-54. XUGuozhuo. Research on path following control for Multi-UUV formation[D]. Harbin: Harbin Engineering University, 2012: 12-54. |
| [14] | FIERRO R, SONG P, DAS Aet al. Cooperative Control of Robot Formations[M]. Philadelphia, US: Springer, 2002, 66: 73-93. |
| [15] | CROWLEY J L. Asynchronous control of orientation and displacement in a robot vehicle[C]//Proceeding of 1989 IEEE International Conference on Robotics and Automation. Scottsdale, AZ: IEEE, 1989: 1277-1282. |
| [16] | 吴瑾斐, 秦东兴, 刘俊.四轮式移动机器人非完整运动控制[J]. 电子科技大学学报, 2007, 36(2): 301-304. WU Jinfei, QIN Dongxing, LIU Jun. Nonholonomic motion control of four-wheeled mobile robot[J]. Journal of University of Electronic Science and Technology of China, 2007, 36(2): 301-304. |
| [17] | 汪超, 唐勇奇. 基于独立C代码的模糊控制器应用程序设计[J].计算机技术与发展, 2009, 19(5): 242-244. WANG Chao, TANG Yongqi. Programmer of fuzzy controller based on stand-alone C-Code[J]. Computer Technology and Development, 2009, 19(5): 242-244. |



