随着MEMS、材料、控制和计算机技术的飞速发展,以及我国快速进入老龄化社会后对康复辅助设备的旺盛需求,穿戴式外骨骼机器人技术在世界范围内引起了越来越多学者的关注。但目前的动力外骨骼和假肢研究存在的一个共性问题是对人体感觉运动控 制、生物力学等知识了解不够,这就导致了虽然设计出了先进的机器人硬件和软件,但由于没有考虑人如何作用,因此设备在与人交互和协同方面效果欠佳。由于人体结构和功能的特殊性和复杂性,建立一个能完全反映人体状态的生物力学模型非常困难。为此,根据研究的目的,对人体或人体的一部分作适当的简化,在一些必要的假设条件下,从不同角度出发,建立人体下肢的生物动力学模型有着巨大的意义[1]。
本文旨在对国内外人体下肢建模和仿真的最新研究状况进行综述,并对今后的研究趋势进行阐述分析,为进一步深入研究下肢生物动力学建模提供一定的参考依据。
1 人体下肢结构概述从解剖学的角度看,人的躯体是由骨、骨连接和骨骼肌组成,全身骨骨间借关节连成骨骼,构成主体人体支架。在运动过程中,骨、骨连接主要起杠杆作用,而具体的肢体关节是运动的枢纽,骨骼肌是运动的动力来源和主要执行部件。
在人体下肢运动中起主要参与的骨骼如下:髋骨、股骨、腓骨、胫骨等。骨与骨之间主要由结缔组织连接,共同形成人体骨架,骨头之间连接的地方称为关节。而在人体下肢运动中起重要作用的关节主要有3个:髋关节、膝关节和踝关节。髋关节为多轴性关节,可做屈、伸、内收、外展、内旋、外旋和旋转运动,由于髋关节起到连接上下肢和承重的作用,其骨密度较大,故而稳固性较好。膝关节是人体负重比例最大、结构最复杂的关节,其主要负责大腿和小腿的屈、伸运动,和某些特定位置下的小幅度旋转运动。踝关节主要负责脚掌的背屈、伸、内收和外展运动。
与此同时,对人体下肢运动充当动力元件的肌肉主要有股直肌、股外侧肌、股内侧肌、腓肠肌、胫骨前肌等。其中股直肌、股内侧肌、股外侧肌主要负责大腿伸和屈、小腿伸和屈、膝关节的伸和髋关节的屈,并保持人体直立姿势;腓肠肌和胫骨前肌主要负责小腿屈伸和人体的直立、行走[2, 3, 4]。
2 人体下肢力学建模方法分类从关节和肌肉角度2个出发,可以得到不同的下肢模型。从关节角度出发可以得到膝关节、髋关节和踝关节力矩;从肌肉角度出发可以得到肌肉力,而且肌肉力进一步可合成关节力矩。考虑到外骨骼发展趋势,操作者的舒适性和安全性变得越来越重要。从个性差异化骨骼肌模型出发的肌肉力模型因与人体下肢结构更为相似,符合人体下肢建模的仿生设计的出发点,具有先天优势,已成为近几年外骨骼的发展热点[5, 6]。
3 基于关节力矩的下肢建模方法由于人体下肢有着复杂的生物结构,并且限于医学伦理性问题,肌肉的生物动力学参数测量具有一定困难,现有的大部分下肢建模方式均未考虑人体下肢的生物模型,只考虑下肢的典型结构,或是建立简化后的下肢多刚体模型[7, 8, 9],或是用3D建模技术模拟简易的人体下肢[10, 11, 12, 13],或是采用黑箱训练等方法跨过人体结构[14],进而通过动力学分析方法描述模型,并对模型进行求解。下面分别介绍几种典型的下肢建模方法。
3.1 Lagrange多刚体模型国内外的许多学者针对人体不同的运动或动作情形,考虑不同情况下模型的具体要求,建立出了相应的多刚体模型,其中最简单的方法是用单质点模拟人体运动,不过模型过于简单,实际价值较低。Hanavan于1964年提出一个由15个多刚体环节组成的,通过球铰系统连接的人体力学模型,这种模型将人体主要的生物结构简化为几何形状的均质刚体,建立并计算出基于人体惯性参数的回归方程,是一套比较完整的具有个性化参数特征的多刚体人体模型,这个模型也在一段时间内被连续引用[15]。波兰学者Blajera等为了研究杂技演员在蹦床上腾空翻跟斗的动作过程,建立了一个自由度为10的多刚体人体模型[16]。Anderson 等在研究人垂直起跳直到达到最大高度过程中肌肉运动协调模式时,把人体简化为10段、具有54块肌肉的模型,并在此模型的基础上进一步建立人在行走过程中行走距离和步态与能量消耗间的关系[17]。Pejhan等在基于步态动力学仿真分析的人体下肢假肢优化系统的设计研究中,将人体下肢简化为 6 刚体的二维力学模型,并使用经典的Lagrange动力学方程对其建模[18]。
多刚体建模方法的核心是不考虑肌肉组成结构,把大腿、小腿、上肢等结构视作一个个刚体,从系统能量或动力学角度,对人体下肢进行建模,其中主要有Newton-Euler方法、Lagrange方法、角动量方法、Kane方法等[19, 20, 21, 22, 23],其中Lagrange 建模法应用最为广泛,下面以这种方法为例介绍典型多刚体建模方法[24]。
Lagrange建模法的核心是建立人体下肢多刚体模型的Lagrange动力学方程。其中,多轴加速度传感器用来检测大腿和小腿的倾角并获取下肢运动过程中的姿态以及膝关节角度和角速度;足底压力传感器被用来检测下肢的脚与地面之间接触状态和作用力等信息。结合人体结构和运动学的分析方法,建立人体下肢运动数学模型。从系统能量角度出发构建动力学模型,并对得到的下肢模型进行动力学分析,进而得到关节力矩。
考虑到人体下肢在行走和跳跃等主要活动中踝关节转动轻微,因此忽略踝关节的转动,将人体下肢结构简化为平面的二刚体模型如图 1所示。其中,H表示髋关节,K为膝关节,A为踝关节。T和S分别代表大腿和小腿的质心。
 |
| 图 1 下肢二刚体二自由度模型 Fig. 1 The two rigid body and two degrees of freedom model of lower limb |
在分析力学中,拉格朗日方程是解决受约束的质点系动力学问题的一个有力工具。拉格朗日函数L被定义为系统动能K和势能P之差,即

其中系统动能K和势能P可以用任何方便的坐标系来表示。用拉格朗日方程表示系统动力学方程式如下:

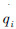 为相应质点的速度,而Fi为作用在第i个坐标上的力或力矩。Ti是作用在第i个坐标上的力或力矩,具体计算公式由qi为直线坐标或角坐标决定。这些力、力矩和坐标分别称为广义力、广义力矩和广义坐标,n为连杆总数目。
为相应质点的速度,而Fi为作用在第i个坐标上的力或力矩。Ti是作用在第i个坐标上的力或力矩,具体计算公式由qi为直线坐标或角坐标决定。这些力、力矩和坐标分别称为广义力、广义力矩和广义坐标,n为连杆总数目。
用Lagrange方程解决实际力学问题是经典力学分析中一种非常成功的方法,具体内容和解题步骤发展都较为成熟。在人体下肢生物动力学模型研究的早期,研究者们多用此方法来描述人体的运动规律。
1)选取关节广义变量及广义力
首先选取笛卡尔坐标系,将大腿和小腿的关节变量分别定义为运动过程中大腿和小腿的转角θ1和θ2,Mh和Mk分别代表髋关节和膝关节的力矩。m1和m2分别表示大腿和小腿的质量,大、小腿长分别为l1和l2,质心分别用T和S代替,与关节中心的距离分别为p1和p2。如上所述,大腿质心T的位置坐标可用一组坐标描述:
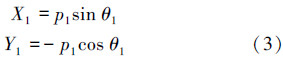
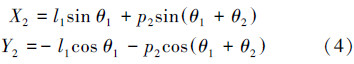
2)系统动能K

3)系统势能P
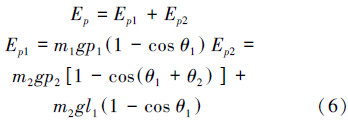
4)拉格朗日函数定义为
L=Ek-Ep5)系统动力学方程
根据拉格朗日方程定义式计算各关节上的力矩,得到系统动力学方程。髋关节H上的力矩Mh 计算如下 :
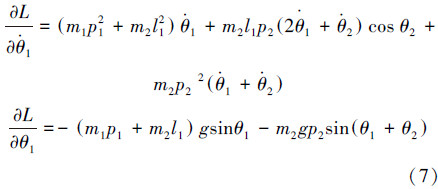
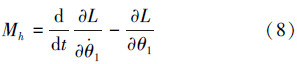


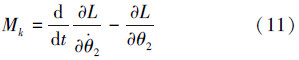

最终得到人体下肢模型如下,带入大腿小腿质量、关节角度等参数即可求得所需要的关节力矩:


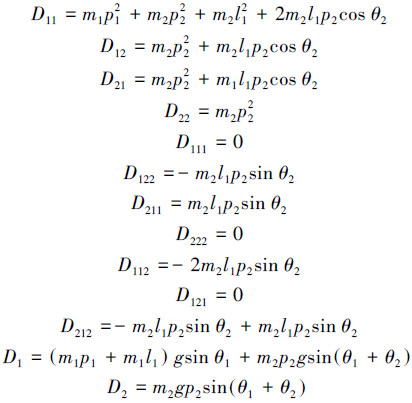
经典动力学研究中的3个定理分别为动量定理、角动量定理和动能定理。Lagrange方程从能量角度出发,应用动能定理和能量守恒建立和求解下肢动力方程,而从角动量定理和动量定理角度出发也可以建立人体多质点模型和多刚体模型的动力学方程[25, 26, 27, 28],求出关节力矩。
动量定理描述了物体的运动状态和力之间的关系,但定义中不涉及力偶或力矩,并且运动量也不涉及角速度和角加速度。而角动量定理则描述了质点系或刚体的运动量和力矩之间的关系。结合这2个定理就可完整地描述外力系与受力体运动参数之间的定量关系。
如图 2所示,质点的运动状态以矢量形式定义:(r、v),相对某参考点的位置矢量为r,速度为v。则动量定理为
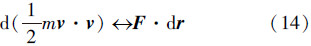
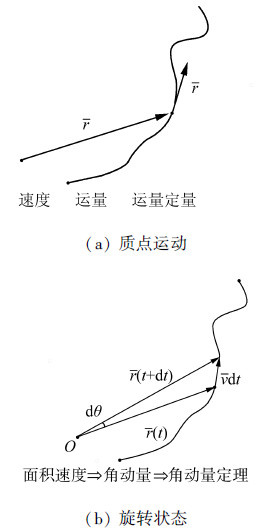 |
| 图 2 质点运动及旋转状态示意图 Fig. 2 Sketch of the motion and rotating state of the particle |
惯性系S中的一个质点在相对某参考点O的运动过程中,其相对参考点O的径矢r会相应的旋转。假设在dt时间质点位移为vdt,转过的角度为dθ,r便会扫过面积dS:
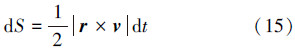

质点在惯性系S中相对参考点O的角动量L:
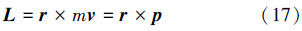
角动量L随时间的变化如下:
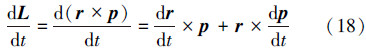
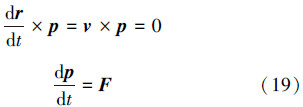

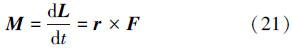
根据下肢的平面二刚体模型,由角动量定理可以得出:
髋关节力矩为
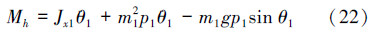
膝关节力矩为
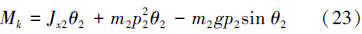
仿真软件建模属于多刚体建模法中的一种,将人体下肢主要结构在ADAMS或SimMechanics等仿真分析或工业设计软件中用一些环节和约束函数代替,再由视频采集软件或运动姿态采集设备提供肢体角度、大小腿长度等输入参数,通过软件强大的仿真功能,直接输出想要得到的关节力矩[29, 30, 31]。
在国内,朱昌义等在研究人体在做单杠摆运动过程特点时,建立了一个5环节组成的多刚体力学模型,并且结合经典力学分析中的Kane方程,推导出人体行走步态规划过程中下肢摆动的动力学方程[32]。刘明辉等在对外骨骼机器的研究中把人体简化成一个九连杆的多刚体模型,并在机械系统动力学自动分析软件(automatic dynamic analysis of mechanical system,ADAMS)中建立了简化后的人体多刚体模型,对人体行走模型及步态分析进行了仿真分析,该研究为在虚拟环境中模拟现实情况下人机外骨骼刚柔耦合系统提供了实验依据[33]。沈凌等在对人体下肢外骨骼假肢的研究过程中,建立了基于四连杆系统的膝关节模型,并利用Lagrange 方法推导出下肢动力学方程,最后在Pro/E(Prol Engineer)软件中建立了下肢假肢结构的仿真模型,通过系统集成的动力学仿真功能,得出的膝关节角度变化和输出力矩之间的关系曲线,为下肢动力学建模提供了一定的参考数据[34]。
洪晓明等人通过Solidworks软件建立精确的三维实体模型,联合Matlab/SimMechanics建立下肢外骨骼康复机器人的动力学模型,以角度、角速度和角加速度作为输入信号,输出信号为髋、膝关节力矩,进行逆动力学仿真分析,获得了外骨骼逆动力学动态数学模型[35, 36, 37]。
3.4 SVR黑箱训练法下肢多刚体模型实质上采用传统的动力学方程求解,具有模型精准度不高,计算关节力矩受参数影响大,不利于实时控制等缺点。针对这些缺点,Wei Meng等提出了SVR黑箱训练法对下肢进行建模,彻底放弃考虑人体下肢结构,并且证明该方法有利于实时控制。该方法从4个下肢肌肉提取的EMG信号均方根值(RMS)作为输入向量,以力传感器采集到的下肢关节力矩作为训练数据,将其输入支持向量回归(SVR)模型来估算下肢关节力矩。使用自回归算法来构建EMG信号和下肢关节力矩之间的关系[38]。
在本方法中,SVR算法被用来预测下肢力量与肌电信号之间的关系。SVR黑箱算法的一个关键问题是用函数来最大限度的接近模型,即找到一个确定性的函数g(x)代替模型本身非确定性函数f(x),可用式(24)进行说明:
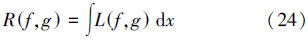
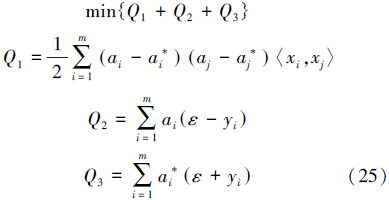
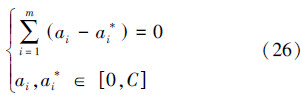
然后,可以得到模型的回归方程:
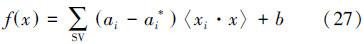
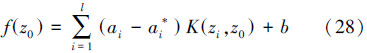
最常用的径向基函数是高斯核函数[40]:
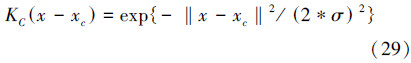
考虑EMG信号与肢体的力之间的关系,从不同情况出发,根据经验公式或者通过对实验数据回归分析得到拉格朗日乘子、网络节点数、宽度参数等训练参数,即可由SVR模型直接推导出关节力矩与EMG信号的关系。
4 基于肌肉力的下肢建模方法从肌肉的本质模型角度出发,骨骼肌力预测有3种代表性的肌肉模型—Hill模型、Huxley模型和流变学模型。其中,应用在下肢建模方面最广泛且最成功的是Hill三元素模型。Nikos Karavas等人提出了一种基于Hill三元素法的下肢模型,下面详细阐述Hill建模法的基本原理[40, 41, 42]。
肌肉的基本机能是把化学能通过做功形式转化为机械能,表征肌肉活动的基本生物力学指标主要有2个:1)肌肉端部测量出来的肌肉对骨骼的拉力,即肌张力;2)运动过程中肌肉纤维长度变化的速度,即收缩速度。这2个指标是与肌肉实际活动密切相关且可测的宏观量。Hill在1938年以青蛙的缝匠肌为试样,做了快速电刺激肌肉释放实验,利用能量原理及经验假设,给出了肌肉收缩力F与收缩速度V间的关系式 :
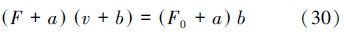
 |
| 图 3 Hill三元素法模型 Fig. 3 Hill Three-element model |
Hill三元素模型考虑肌肉的本质结构,将肌肉简化为3种元素,即收缩元PE、串联弹性元SE和并联弹性元CE来反映肌肉的功能。用一个弹簧阻尼系统代表肌肉模型,如图 4所示。
 |
| 图 4 基于超微结构和肌丝结构的骨骼肌模型 Fig. 4 Skeletal muscle model based on ultrastructure and muscle wire structure |
该模型中,各种元素的意义和肌肉的超微结构一一对应。收缩元代表着滑动的肌动蛋白和肌球蛋白分子,串联弹性元代表肌节和结缔组织的固有弹性,并联弹性元代表连接肌肉骨骼的结缔组织。
肌肉力是由于神经电信号对肌肉收缩单元的刺激产生的,因此Hill肌力模型应考虑2个关键问题,分别为“EMG-激活程度”和“激活程度-肌力”之间的关系描述。前者表示了神经电刺激与实验测得的表面肌电信号之间的潜在关系,后者则表示了肌肉的激活程度同所产生的肌张力之间的关系。在Hill三元素模型图中,lmt为肌腱和肌纤维的总长度,lt为肌腱长度,lm为肌纤维长度,α为肌肉纤维束与肌腱的夹角。
根据上诉的三元素结构,肌肉力的生成用弹簧阻尼系统动力学方程来描述,其中肌腱单元所产生的合力如下:

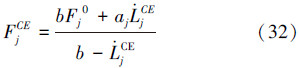
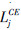 分别表示肌肉的长度和收缩速度,Fj0等张力则由式(33)给出:
分别表示肌肉的长度和收缩速度,Fj0等张力则由式(33)给出:
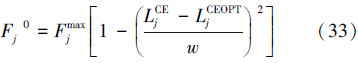
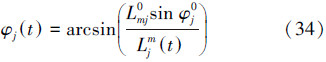
肌电信号是目前测量肌肉激活程度的唯一手段。但由于SEMG信号在实验测量中容易受到表面湿度、皮下脂肪等因素的干扰,原始的EMG信号往往很难直接应用于肌力预测,必须经过一系列的数字信号处理才能使用。依据Hill肌力模型,肌肉激活程度表现为0~1的某个数值。0表示肌肉没有任何激活,1则表示肌肉完全激活。这是2种极端情况,实际中肌肉激活程度是介于0~1的常数,其值大小可通过归一化实验处理得到或者通过模糊推理机得到。本文以模糊推理机为例介绍基于Hill模型的下肢建模方法[43]。
模糊理论是随着模糊数学的出现而蓬勃发展的,其核心是确定0~1的隶属度函数值,非常适合于估计SEMG的肌肉激活常数。本方法根据采样得到的EMG信号,通过对其进行模糊化处理,经过一系列模糊规则推理,采用模糊隶属度函数来表示肌肉激活程度,从而作为Hill肌肉模型的输入,再根据个人差异化肌肉参数,输入到Hill三元素模型,进行肌肉力的预测计算,具体流程如下。
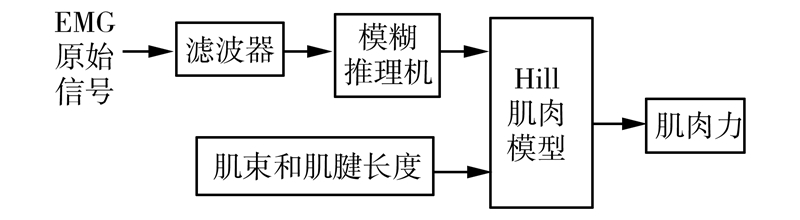 |
| 图 5 Hill肌力预测模型流程图 Fig. 5 Flow chart of Hill muscle strength prediction model |
模糊逻辑推理模型主要有Mamdani和Sugeno两种方法。首先,将采样得到的EMG原始信号进行滤波和平滑处理;其次对EMG原始信号进行滤波和平滑处理,将其用模糊集进行表示。然后建立模糊推理规则,根据处理后的EMG信号幅值,推理出作为肌肉激活程度的隶属度函数。然后结合肌束和肌腱的长度,通过Hill肌力模型,从而计算出肌肉力。在Matlab中的模糊工具箱中设计了模糊推理规则和隶属度函数,通过Matlab编程,实现对Hill肌力预测模型的计算。
计算出肌肉力之后,就可以从力矩的定义出发,将肌肉力与各自的力臂相乘,之后对关节进行简单的受力分析,得出所需要的关节力矩[44, 45, 46]。
肌肉力臂ri(t)可通过对骨骼肌长度和形状求导得到,公式如下:
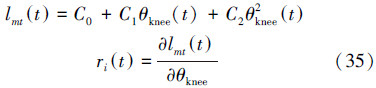
代入后得到力臂ri(t),其中,C0、C1和C2均为常数。

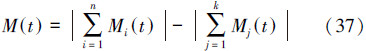
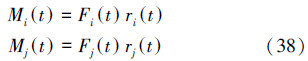
下肢建模的仿真验证是建模过程中的重要一环,也因为真实值测量困难、参数复杂多样等因素一直是建模过程中的难点。目前国内外对下肢建模的仿真验证主要采取以下几种方法。
孙棕檀等人将基于Lagrange方程或Kane方程等传统动力学分析的结果,与Simulink等仿真软件输出的结果进行比较分析,证明了传统力学分析应用在下肢建模具有一定的可行性[47]。
Wei Meng等将SVR黑箱训练计算出的关节力矩与实验中力矩检测装置反馈回的真实值进行比较分析,结果证明模型准确度较高,EMG信号与关节力矩匹配情况较好,模型具有较高的应用意义[48]。陈贵亮等人使用实验数据经过BP神经网络训练,对模型进行辨别,确定模型中的未知参数,并使用额外的数据去验证模型的准确度,有一定参考价值[49]。
Nikos Karavas等从表面肌电信号出发,验证得到的肌肉力或转矩与真实人体行走过程中记录下的EMG和扭矩波形进行趋势比较和均方根误差分析,证明模型的精准度较高,对仿真验证算法有着较高的指导意义[50]。
6 结论人体是一个非常复杂的多体模型。国内外研究者针对人体不同的运动或动作,对人体做出了相应的多刚体简化模型,并使用不同的建模方法建立了人体运动的动力学方程,取得了一些有意义的成果。但将人体简化为多刚体模型,忽略了肌肉和神经系统的作用,模拟的人体运动系统缺乏灵活性和自适应性。因此,所建的模型与人体实际运动情况具有较大差异。
SVR和仿真软件建模法也各有利弊。SVM模型法的优点是模型简单,但核心参数的选取还没有统一的理论公式,准确度有待提高。仿真软件建模优点是下肢参数考虑较为完全,但缺点是数据需要引出,并且计算量较大不利于实时控制。
相比较而言基于Hill三元素模型建立的人体下肢模型更为贴近人体的实际下肢结构,对人体运动的建模和仿真更符合人体实际运动状态。由于人体的运动过程非常复杂,而且每一时刻都会有不同的状态,应该根据不同的需求建立不同的模型。为了得到更加符合实际的模型,我们需要在现有建模技术的基础上,更加深入的考虑人体的生理结构,将外骨骼与操作者的行走习惯有机结合在一起,兼顾人的意愿和外界作用力的影响,采用合理的控制策略,提高系统的鲁棒性,达到最优的控制目的。
| [1] | DOLLAR A M, HERR H. Lower extremity exoskeletons and active orthoses: challenges and state-of-the-art[J]. IEEE Transactions on Robotics, 2008, 24(1): 144-158. |
| [2] | 吕厚山. 人工关节外科学[M]. 北京: 科学出版社, 2001: 1-799. LYU Houshan. Artificial Joint Surgery[M]. Beijing: Science Press, 2001: 1-799. |
| [3] | MOEINZADEH M H, ENGIN A E, AKKAS N. Two-dimensional dynamic modeling of human knee joint[J]. Journal of Biomechanics, 1983, 16(4): 253-264. |
| [4] | ROYER T, KOENIG M. Joint loading and bone mineral density in persons with unilateral, trans-tibial amputation[J]. Clinical Biomechanics, 2005, 20(10): 1119-1125. |
| [5] | YANG C J, ZHANG J F, CHEN Y, et al. A review of exoskeleton-type systems and their key technologies[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2008, 222(8): 1599-1612. |
| [6] | KAZEROONI H. Human augmentation and exoskeleton systems in Berkeley[J]. International Journal of Humanoid Robotics, 2007, 4(3): 575-605. |
| [7] | BRAND R A. The biomechanics and motor control of human gait: normal, elderly, and pathological[M]. Waterloo: University of Waterloo Press, 1991: 14-15, 1-384. |
| [8] | TUMER S T, ENGIN A E. Three-body segment dynamic model of the human knee[J]. Journal of Biomechanical Engineering, 1993, 115(4A): 350-356. |
| [9] | MOEINZADEH M H, ENGIN A E, AKKAS N. Two-dimensional dynamic modeling of human knee joint[J]. Journal of Biomechanics, 1982, 15(4): 346. |
| [10] | AYOUB M M. A 2-D simulation model for lifting activities[J]. Computers & Industrial Engineering, 1998, 35(3-4): 619-622. |
| [11] | PANDY M G, ZAJAC F E, SIM E, et al. An optimal control model for maximum-height human jumping[J]. Journal of Biomechanics, 1990, 23(12): 1185-1198. |
| [12] | SPÄGELE T, KISTNER A, GOLLHOFER A. Modelling, simulation and optimisation of a human vertical jump[J]. Journal of Biomechanics, 1999, 32(5): 521-530. |
| [13] | Anolg Devices, Inc. ADXL203 Data Sheet[DB/OL]. [2006-04-27]. |
| [14] | FAN Yuanjie, YIN Yuehong. Active and progressive exoskeleton rehabilitation using multisource information fusion from EMG and force-position EPP[J]. IEEE Transactions on Biomedical Engineering, 2013, 60(12): 3314-3321. |
| [15] | HANAVAN E P. A mathematical model of the human body.AD608463[R][S.l.], 1964. |
| [16] | BLAJER W, CZAPLICKI A. Modeling and inverse simulation of somersaults on the trampoline[J]. Journal of Biomechanics, 2001, 34(12): 1619-1629. |
| [17] | ANDERSON F C, PANDY M G. Dynamic optimization of human walking[J]. Journal of Biomechanical Engineering, 2001, 123(5): 381-390. |
| [18] | PEJHAN S, FARAHMAND F, PARNIANPOUR M. Design optimization of an above-knee prosthesis based on the kinematics of gait[C]//30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Vancouver, Canada, 2008: 4274-4277. |
| [19] | 张国伟, 宋伟刚.并联机器人动力学问题的Kane方法[J].系统仿真学报, 2004, 16(7): 1386-1391. ZHANG Guowei, SONG Weigang. A Kane formulation for the inverse dynamic of Stewart platform manipulator[J]. Journal of System Simulation, 2004, 16(7): 1386-1391. |
| [20] | 刘延斌, 韩秀英, 薛玉君, 等.3-RRRT并联机器人动力学仿真[J].系统仿真学报, 2006, 18(7): 1962-1965. LIU Yanbin, HAN Xiuying, XUE Yujun, et al. Dynamics simulation of a 3-RRRT parallel robot[J]. Journal of System Simulation, 2006, 18(7): 1962-1965. |
| [21] | TIBERT G. Deployable tenegrity structures for space application[R].Stockholm: Royal Institute of Technology, 2002. |
| [22] | JENKYN T R, NICOL A C. A multi-segment kinematic model of the foot with a novel definition of forefoot motion for use in clinical gait analysis during walking[J]. Journal of Biomechanics, 2007, 40(14): 3271-3278. |
| [23] | SMITH S L. Application of high-speed videography in sports analysis[C]//Proceedings of SPIE 1757, Ultrahigh- and High-Speed Photography, Videography, and Photonics. San Diego, USA, 1992: 118. |
| [24] | NARUSE K, KAWAI S, KUKICHI T. Three-dimensional lifting-up motion analysis for wearable power assist device of lower back support[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton, Canada, 2005: 2959-2964. |
| [25] | KIGUCHI K, HAYASHI Y. Estimation of joint torque for a myoelectric arm by genetic programming based on EMG signals[C]//IEEE World Automation Congress (WAC). Puerto Vallarta, Mexico, 2012: 1-4. |
| [26] | SARTORI M, REGGIANI M, PAGELLO E, et al. Modeling the human knee for assistive technologies[J]. IEEE Transactions on Biomedical Engineering, 2012, 59(9): 2642-2649. |
| [27] | PATRINOS P, ALEXANDRIDIS A, NINOS K, et al. Variable selection in nonlinear modeling based on RBF networks and evolutionary computation[J]. International Journal of Neural Systems, 2010, 20(5): 365-379. |
| [28] | SONG R, TONG K Y. Using recurrent artificial neural network model to estimate voluntary elbow torque in dynamic situations[J]. Medical and Biological Engineering and Computing, 2005, 43(4): 473-480. |
| [29] | 金德闻, 王人成, 白彩勤. 电流变液智能下肢假肢摆动相控制原理与方法[J].清华大学学报:自然科学版, 1998, 38(2): 40-43. JIN Dewen, WANG Rencheng, BAI Caiqin. Swing phase control of intelligent lower limb prosthesis using electrorheological fluid[J]. Journal of Tsinghua University: Science and Technology, 1998, 38(2): 40-43. |
| [30] | MARTINEZ-VILLALPANDO E C, MOONEY L, ELLIOTT G, et al. Antagonistic active knee prosthesis. A metabolic cost of walking comparison with a variable-damping prosthetic knee[C]//Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Boston, USA, 2011: 8519-8522. |
| [31] | 王斌锐, 金英连, 徐心和.仿生膝关节虚拟样机与协同仿真方法研究[J].系统仿真学报, 2006, 18(6): 1554-1557. WANG Binrui, JIN Yinglian, XU Xinhe. Virtual prototype and collaborative simulation of bionic knee joint[J]. Journal of System Simulation, 2006, 18(6): 1554-1557. |
| [32] | 朱昌义. 单杠上人体摆动的凯恩动力学模型[J]. 成都体育学院学报, 2000, 26(6): 71-74. ZHU Changyi. Kaine dynamics model of human swing on the horizontal bar[J]. Journal of Chengdu Sport University, 2000, 26(6): 71-74. |
| [33] | 刘明辉, 顾文锦, 陈占伏. 基于骨骼服的虚拟人体建模与仿真[J]. 海军航空工程学院学报, 2009, 24(2): 157-161. LIU Minghui, GU Wenjin, CHEN Zhanfu. Virtual human body modeling and simulation based on skeletal services[J]. Journal of Naval Aeronautical and Astronautical University, 2009, 24(2): 157-161. |
| [34] | 沈凌, 孟青云, 喻洪流. 基于虚拟样机技术的下肢假肢结构设计与仿真[J]. 工程设计学报, 2011, 18(1): 34-38. SHEN Ling, MENG Qingyun, YU Hongliu. Design and simulation of leg prosthesis structure based on virtual prototype technology[J]. Journal of Engineering Design, 2011, 18(1): 34-38. |
| [35] | MOURAGNON E, LHUILLIER M, DHOME M, et al. Monocular vision based SLAM for mobile robots[C]//IEEE International Conference on Pattern Recognition. Hong Kong, China, 2006, 3: 1027-1031. |
| [36] | PRATT J, CHEW C M, TORRES A, et al. Virtual model control: An intuitive approach for bipedal locomotion[J]. The International Journal of Robotics Research, 2001, 20(2): 129-143. |
| [37] | YUAN Shaoqiang, LIU Zhong, LI Xingshan. Modeling and simulation of robot based on Matlab/SimMechanics[C]//Proceedings of the 27th Chinese Control Conference. Kunming, China, 2008: 161-165. |
| [38] | XU Guozheng, SONG Aiguo, LI Huijun. Control system design for an upper-limb rehabilitation robot[J]. Advanced Robotics, 2011, 25(1-2): 229-251. |
| [39] | RARNJANI A N, CORSS P A. A Kalman filter model of an integrated land vehicle navigation system[J]. Journal of Navigation, 1995, 48(2): 293-302. |
| [40] | HARDYK A T T. Force and power-velocity relationships in a multi-joint movement[D]. Pennsylvania State: The Pennsylvania State University, 2000: 102-123. |
| [41] | FENN W O, MARSH B S. Muscular force at different speeds of shortening[J]. The Journal of Physiology, 1935, 85(3): 277-297. |
| [42] | POLISSAR M J. Physical chemistry of contractile process in muscle. I. A physicochemical model of contractile mechanism[J]. The American Journal of Physiology, 1952, 168(3): 766-811. |
| [43] | SHADMEHR R, ARBIB M. A mathematical analysis of the force-stiffness characteristics of muscles in control of a single joint system[J]. Biological Cybernetics, 1992, 66(6): 463-477. |
| [44] | VISSER J J, HOOGKAMER J E, BOBBERT M F, et al. Length and moment arm of human leg muscles as a function of knee and hip-joint angles[J]. European Journal of Applied Physiology and Occupational Physiology, 1990, 61(5-6): 453-460. |
| [45] | AN K N, TAKAHASHI K, HARRIGAN T P, et al. Determination of muscle orientations and moment arms[J]. Journal of Biomechanical Engineering, 1984, 106(3): 280-282. |
| [46] | OSU R, FRANKLIN D W, KATO H, et al. Short-and long-term changes in joint co-contraction associated with motor learning as revealed from surface EMG[J]. Journal of Neurophysiology, 2002, 88(2): 991-1004. |
| [47] | 孙棕檀. 刚柔耦合系统分析动力学建模研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 44-56. SUN Zongtan. Research on dynamic modeling analysis of rigid flexible coupling system[D]. Harbin: Harbin Engineering University, 2013: 44-56. |
| [48] | MENG Wei, DING Bo, ZHOU Zude, et al. An EMG-based force prediction and control approach for robot-assisted lower limb rehabilitation[J]. IEEE International Conference on Systems, Man, and Cybernetics. San Diego, USA, 2014: 2198-2203. |
| [49] | 陈贵亮, 李长鹏, 赵月, 等. 下肢外骨骼康复机器人的动力学建模及神经网络辨识仿真[J]. 机械设计与制造, 2013, (11): 197-200. CHEN Guiliang, LI Changpeng, ZHAO Yue, et al. Dynamic modeling and neural network identification simulation for lower limbs exoskeletons rehabilitation robot[J]. Mechanical Design and Manufacture, 2013, (11): 197-200. |
| [50] | KARAVAS N, AJOUDANI A, TSAGARAKIS N, et al. Tele-impedance based assistive control for a compliant knee exoskeleton[J]. Robotics and Autonomous Systems, 2014, doi: 10.1016/j.robot.2014.09.027. |



