2. 北华大学 电气信息工程学院, 吉林 吉林 132000
2. Electric & Information Engineering, Beihua University, jilin, 132000 China
在自然界和社会中的复杂网络代表实体在非均匀系统之间的相互作用,随着复杂网络和图形数据的增长,网络结构比对的应用在过去10年呈爆炸式增长。尤其是随着化学实验测定技术[1, 2]和文献挖掘技术[3]的发展产生了大量的生物网络数据。现实世界复杂网络主要包括社会网络、信息网络、技术网络和生物网络。从宏观方面分析,复杂的网络可以从度分布、特征路径长度以及聚集系数上来分析;从微观方面分析,复杂网络包括网络模体,例如小子图更可能表现出网络的重要性质;中级的子图更容易表现出网络的社区性和模块性[3]关于复杂网络的研究是从欧拉的七桥问题研究开始的,复杂网络通过结点之间的相互作用关系来表示,所以复杂的网络关系可以用图G=(V,E)表示,其中V代表结点的集合,E代表边缘的集合。分析复杂网络的数学理论基础是Erdos[4]提出的关于随机网络的生成及演化的理论。复杂网络结构比对问题是在2个网络或者多个网络中找到最佳匹配的结点之间映射关系的优化问题,是一种放松的图同构问题[5]并且它与子图同构问题[6]密切相关。网络结构比对问题最先应用在模式识别和计算机视觉[7]上。在模式识别上的应用主要是在大的模块中识别小的模块,在计算机视觉的应用主要是进行图片的比较。在本体定位应用程序[8, 9, 10]和生物信息学上也有非常广泛的应用,例如在数据库中找到匹配的数据[11];在蛋白质相互作用网络、代谢网络、基因表达网络、基因调控网络和信号传导网络等都有实际的应用。对于生物网络的比对问题,有着实际的意义,通过已知生物网络比对未知生物网络,可以发现更多的生物网络结构,对研究未知的生物领域有着很重要的作用。在现实生活中同样存在着大量的复杂网络,例如信息网络、交通网络、电力网络、社交网络、生物网络、P2P网络、语言网络、公交网络等等,这些网络与人们日常生活密切相关,因此这就需要深入研究复杂网络的拓扑结构动力学行为和演化机制等,以便更好地设计这些复杂网络和控制他们的行为。
1 复杂网络的比对问题1)复杂网络结构比对问题的定义:2个已知的复杂网络,网络G=(V,E)和网络H=(U,F),结点v∈G,结点u∈H,存在一个映射关系a,映射关系满足下面要求:
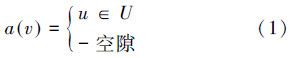
网络结构比对问题就是要找到不同网络顶点之间的映射关系,使得网络结点的相似性得分最高,如图 1所示。
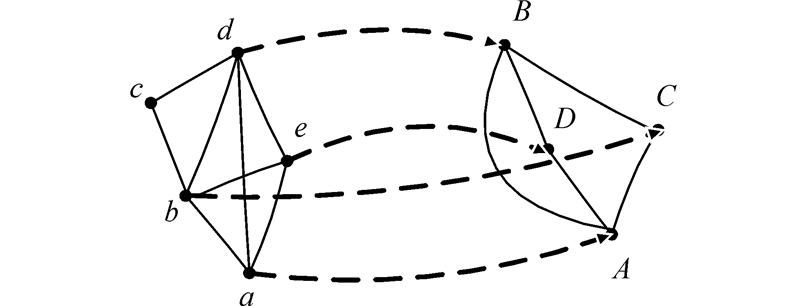 |
| 图 1 a映射下的结点比对图 Fig. 1 Note alignment under a mapping |
虚线箭头表示结点v∈G到结点u∈H的映射关系:a(v)=u,其中没有被标记的结点表示映射到一个空隙。
2)网络结构比对中相似度函数的定义
相似度函数是2个网络结构比对的相似性得分的计算公式,其形式化定义如下:
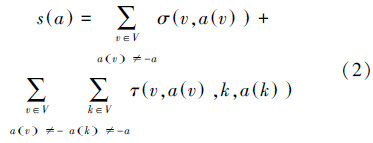
3)复杂网络的比对图概念:复杂网络的比对问题可以看作图的比对问题。复杂网络中的结点对应于图的顶点,复杂网络中结点之间的相互作用对应图的边。
比对图V∪U是一个加权的完全比对二分图,是V∪U的结点集合。边缘权重e=(v,u)是w(e)=σ(v,u)。网络结构比对图如图 2。
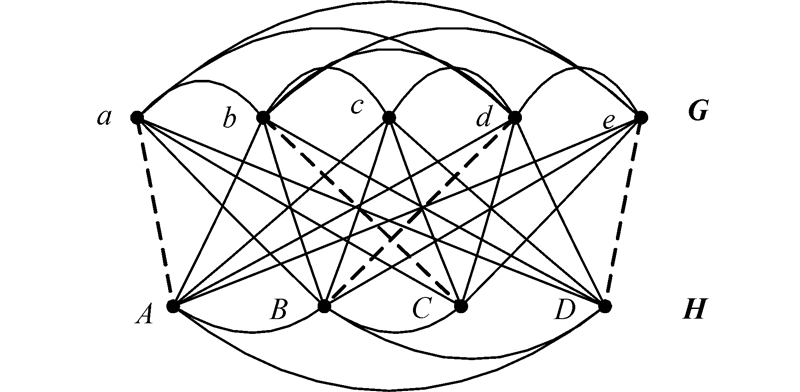 |
| 图 2 网络结构比对实例 Fig. 2 The case of construction alignment of complex networks |
这是一对一映射的网络结构比对图。在比对a之间建立连接,结点的顺序对比对结果没有影响,这个比对图具有图匹配的理论概念的特点,比对的图是不会有2个被选择的边缘分享一个结点的子集的情况。它提供了一种替代的方式来表示网络中结点的比对。
2 复杂网络比对方法的分类复杂网络的比对模型和算法是复杂网络比对方法核心内容:复杂网络的比对模型是对复杂网络比对问题的抽象和数学建模,主要通过复杂网络本身的特性和具体问题的特点来进行比对模型的构建;网络的比对算法指的是比对模型上的可计算步骤,用来计算网络的比对模型。本节主要从复杂网络的比对模型方面对复杂网络比对方法进行分类探讨。通过对近年来的网络结构比对方法进行总结,本文主要把网络的比对方法归结为基于图的网络结构比对方法、基于数学框架网络结构比对方法。
基于数学框架网络结构比对方法是一类优化问题,具有一般优化问题的特征,这种方法将网络的比对问题转化为常规的优化问题,采用已知的求解方法进行求解;将网络比对问题中的匹配准则转化为优化问题的约束条件。
基于图的网络结构比对算法是目前研究网络结构比对算法中应用最多的一种算法。它是一种将网络的比对问题转化为图的比对问题的算法。首先要在进行比对的2个网络中构建一种映射关系,然后建立模型进行网络结构比对。
2.1 基于数学框架网络结构比对方法基于数学编程框架网络结构比对方法是一种目标函数的约束优化方法。基于数学编程框架网络结构比对方法主要分为整数二次规划法和矩阵特征值法。其中整数二次规划法的代表方法是Klau′s的简单的启发式算法[12]和置信传播(BP)快速启发式的算法,矩阵特征值法的代表方法是Isorank[13, 14]方法。
2.1.1 整数二次规划法对于整数二次规划法,首先规范定义网络结构比对的数学问题,对整数二次规划的问题进行求解;然后使用简单的启发式算法释放整数二次规划问题的完整约束,解决已有的线性规划问题,计算网络中边缘权重得分;最后在网络结构比对中使用最大权重二分图进行比对。整数二次规划定义规范[15]如下。
L是权重二分图,L=(V∪U,EL,w),α和β是正常数,G、H、L和α、β是输入数据,把这些数据设为已知量,其中L中的匹配集合M是EL的子集,如果(v,u)和(k,l)在匹配集合M中,称之为网络G中边缘(v,u)与网络H中的边缘(k,l)是重叠的。这个网络结构比对问题就是在L中找到最大的匹配M。α是匹配集合M的权重值,β是网络G和网络H重叠的边缘数。w是任意结点的边缘权向量,wv,u表示边缘的向量,边缘(v,u)在M中xv,u=1时,也就是说xv,u=1时结点v,u完全匹配,当矩阵S是对应EL的边。x表示2个比对网络中对应的结点比对关系。
线性匹配约束条件为
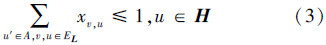
个权重向量A,B和一个权重矩阵C[6]。这2个权重向量分别为在网络结构比对过程中网络G中结点到网络H中结点的权重二分图L中每个边的对数似然函数和网络H中结点到网络G中结点的权重二分图L中每个边的对数似然函数和;权重矩阵是指比对结果中边缘重叠的对数似然函数。这些权重值被叫做消息。在每次更新消息后,都要在二分图比对过程中循环消息,之后重新评价目标函数。
置信传播算法方法[28, 29]是一种很有效的求解条件边缘概率的方法。通过局部的消息传递,网络中的每个结点通过和邻近结点交换信息对自身的概率状况进行评估,更新准则由已知变量推理未知变量。通过这种方式,使得计算量从指数增长变成近似的线性增长,从而使得统计推断能在复杂系统中被应用。置信传播方法(BP)可以正确的找到优化问题的最优解,当然也包括最大权重的匹配问题。
2.1.2 并行网络一致性的实现网络结构比对的并行运算是使用OpenMP[30]共享内存并行系统的多线程程序。所有需要的内存是在第1次迭代之前设定的。没有动态内存的分配并且要避免计算中间结果,并行比对的矩阵都是系数矩阵并且以压缩的稀疏行数组的形式保存。考虑到矩阵S的不确定性,使用动态的OpenMP[31]的并行算法会比静态的算法有更好的效果。
在更新矩阵的时需要额外的并行运算,Klau′s算法的迭代过程不依赖于二分图的比对过程,但是置信传播(BP)算法需要解决二分图比对问题,因为B、C迭代的质量会随着它的迭代而变化。由于最后跌迭代的结果往往不如中间迭代的结果,所以需要保存最后几步迭代的结果,同时对这些结果的质量进行评估。要对不好的结果进行成批的舍去,提高代码的伸缩性。
以上算法主要应用在生物网络结构比对方面[32]和本体比对方面[8, 9, 33]。
2.1.3 矩阵特征值法矩阵特征值法是一种基于谱的比对方法。它通过矩阵建立网络结构比对模型,使用矩阵的特征值计算比对网络的结点相似性,最后使用搜索算法得到网络结构比对的结果。以矩阵的特征值计算结点相似的方法是由PageRank算法[34]首先提出来的,Isorank方法把这种算法应用到网络结构比对的计算中。结点对比对的基本思想是只有结点对的相邻结点对相似它们才可能有相似关系。这个思想阐述了结点与邻居结点紧密相连的关系。IsorankN算法[35]同样是应用此种思想,不同的是IsorankN算法使用在k部图上运行。通过谱聚类算法PageRank Nibble[36]比对相似功能模块。算法SPINAL[37]也是秉承Isorank算法中结点对的比对的思想,但是它在此基础上提出了结点相邻结点的集合(N(V),N(U))的概念。
2.1.4 Isorank算法的基本思想由图 3所示a、b、c、d、e是网络G中的结点;a′、b′、c′、d′、e′是网络H中的结点。结点对(a,a′)的相似得分是由它们的相邻结点(b,b′)的相似性决定。因为结点a和结点c都与结点b相邻,所以结点b对a的贡献是1/2,同理结点b′对结点的贡献也是1/2。所以可以得到结点对(a,a′)和结点对(b,b′)的关系式Raa,=Rbb,/4依次关系可以得到如下结点的关系:
 |
| 图 3 结点比对图 Fig. 3 Network of note alignment |
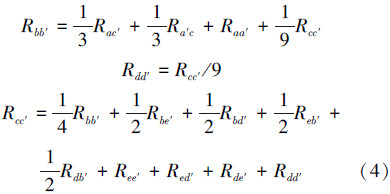
N(V)和N(U)表示结点v和结点u的相邻结点,w(e)表示边缘权重值,Ri,j表示结点对i,j的相似得分。依据结点得分方法可得到结点比对的矩阵定义公式:

R是A矩阵特征值所对应的特征向量。由随机矩阵A的性质可知,1是矩阵A的模最大的特征值,R是A矩阵模最大的特征值对应的特征向量。通过使用幂方法[37]求解R。幂方法是按照更新法则(6)不断更新R得到的,其中R(k)表示对R的k次迭代。
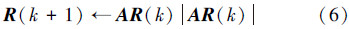
通过上述步骤构建比对问题的模型。把比对问题转化为通过幂方法求解求矩阵的特征值问题,得到结点相似得分R。最后使用贪婪算法提取出结点对的映射关系。
2.1.6 基于数学框架网络结构比对方法的特点1)构建复杂网络结构比对的规范数学公式。例如整数二次规划问题和矩阵特征值问题。
2)规范数学公式求解问题。例如采用拉格朗日松弛法\置信传播算法以及幂方法求解。
3)解的映射关系的提取。在得出结点对的相似得分之后,需要把比对的结果还原到原来的网络中,对最大相似区域的进行比对。
2.2 基于图的网络结构比对方法基于图的网络结构比对方法从比对范围可分为全局网络结构比对方法、局部网络结构比对方法。全局网络结构比对方法对结点的映射关系有一定的限制,结点之间的映射关系必须是一一对应的关系。局部网络结构比对方法是在2个网络中找到局部的同构区域,其中局部的区域是独立的映射关系。与全局网络结构比对不同的是,局部网络结构比对的结点的映射关系可以是多对一或者一对多的关系。从比对结果上来说,全局比对可以得到唯一精确的最大的公共子图的比对结果,局部比对得到的是局部最优的比对结果。但是当使用不同的局部比对算法常常会得到不同的比对结果。所以从实际应用上来分析,2种方法有各自的优缺点。局部蛋白质比对的研究算法已经相对成熟,全局蛋白质网络结构比对算法还在深入探索中。
PathBLAST[38]算法通过考虑被比对的结点的同源性和结点数据在路径上正确概率上来搜索高分途径的局部网络结构比对方法。NetworkBLAST[39]算法是通过发现保守的结点集群进行比对的方法,它的特点是通过建立likelihood-based模型得到结点权重值和边缘权重值的比对图,把网络结构比对问题转化通过启发式算法搜索权重最大子图问题。权衡子网络的密集程度和类似随机子网络结构的密集程度,有利于提高比对结果的统计显著性,它能够同时比对多个网络。MaWISh[40]算法通过evolution-based分数表来确定保守集群。它延伸了在序列比较中的进化事件的概念,把序列比对中的空隔、匹配和失配扩展为网络结构比对中的复制、匹配和失配,并通过记分函数评估网络结构的相似结构。Graemlin[41, 42]算法是第1个能够识别任意结构的保守子网的密度的算法。它是一种基于“seed-and-extend”的贪婪算法。它可以识别不同物种的进化保存功能模块。通过计算模块受进化约束比率的log-ratio给模块打分,并且在比对中模块是不受限制的。这种方法既可以进行全局比对,也可以局部比对。MHA方法[43]通过ProportionalHill[44]算法定义结点成员性的概念。结点成员性概念可以确定在什么范围内结点可以参与到功能模块上,从而确保提取到完整的不受破坏的功能模块。HopeMap算法[24]提出一个通用的评分系统,用来寻找最高得分的子图。在考虑结果的应用性时,在比对过程中就把要求的比对结果的相关信息融入算法中。
下面主要介绍一种可以应用于任何网络的基于图拓扑结构网络结构比对算法。
2.2.1 基于图拓扑结构网络结构比对算法GRAAL算法[45, 46]是典型的基于拓扑结构的网络结构比对算法,GRAAL算法只需要网络的拓扑结构信息,不需要其他的网络的先验信息。它可以应用到各种类型的网络结构比对中,包括生物网络结构比对,社交网络结构比对等。在文献[47]中首次在网络结构比对问题中提出标签相似(signature similarity)概念。
1)标签相似
诱导子图的结点x∈v并且结点x在网络G中相连的边缘也都在诱导子图中。对于所有的2~5个结点的诱导子图,在考虑结点在诱导子图的对称性时,2~5个结点的诱导子图会有73种不同的轨迹。如图 4~7所示。2~5个结点的73个轨道是描述结点的相邻拓扑关系的一种标签并且可以确定到与这个结点的距离的相互联系。
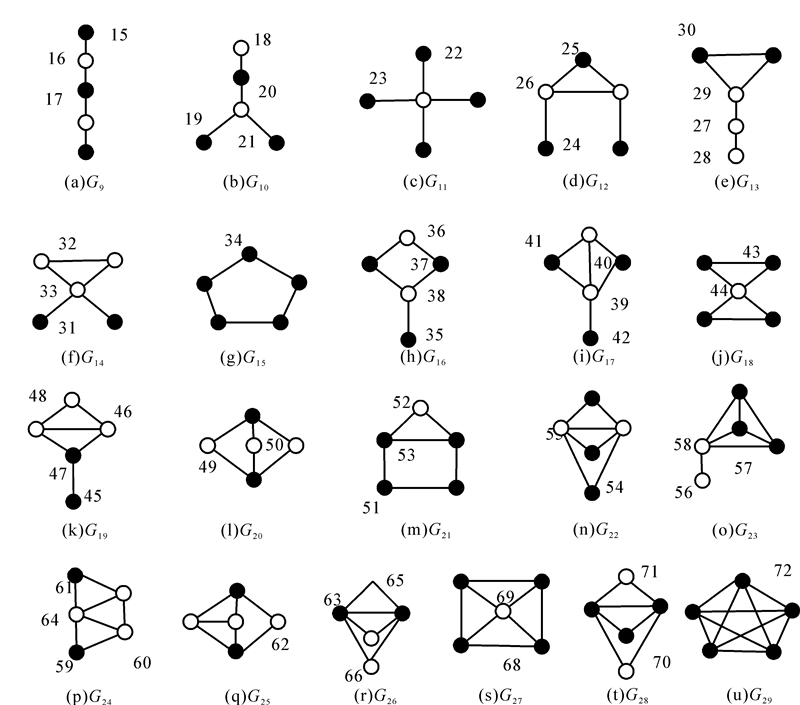 |
| 图 7 5节点诱导子图的轨迹 Fig. 7 Track of induced subgraph of 5 notes |
在i方向上的结点对(v,u)的距离如式(7)所示:结点u∈G,ui表示结点在i方向上的标签向量,即结点u在i这个方向上出现的次数。
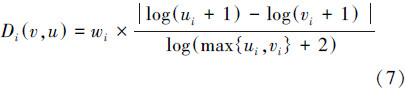
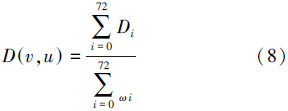
把结点对D(v,u)标签相似得分S(v,u)公式如式(9)所示:
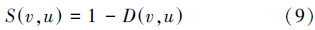
D(v,u)的值越大,表示在u,v这2个结点上有更相似的拓扑结构。
2)结点对得分公式
结点对的相似得分随着结点的度的变化而改变,结点的度越大,结点的相似性就越低,在相同的标签相似中它的结构更紧凑。
结点对的相似得分公式如式(10):

3)网络结构比对算法
首先选择最小值的C(V,U)为种子结点。然后以种子结点为中心向外扩展,进行搜索,搜索时遵循一定的规则,可假设存在一个球体,这个球体的圆心分别为种子结点v和u,半径为任何可能的一个定值,之后通过greed算法找到结点(u′,v′)对集合其中v′∈SG(v,r)={x∈v:d(v,x)=r},其中公式中u′∈SH(u,r)。最后将结点对集合(u′,v′)中所有的结点进行比对,找出最小C值的结点对。
H-GRAAL算法是GRAAL算法的改进算法。这种算法得到一个最优的网络结构比对集合。H-GRAAL算法进行比对的时候采用了动态的匈牙利算法[48]。对于动态匈牙利算法只需要改变匈牙利算法[49]返回的最优结点对(v,u)的C值。
C-GRAAL算法[50]提出了在网络结构比对结点相邻结点的共同结点的概念。C-GRAAL算法是在GRAAL算法的基础上加入相邻结点的共同结点的比对。如果具有最大值的共同结点的结点相似得分很高,就将结点保留,否则,将结点从比对结果中删除,反之,如果已经比对的结点对的相似得分很大,但是却没有共同相邻结点,同样删除。
GRAAL算法和H-GRAAL算法属于基于集群的算法。与其他算法通过密集的相互连接的区域定义集群不同,GRAAL算法把具有相同拓扑特征的结点集或者属于相同网络区域定位集群,属于相同的拓扑结点不需要相互连接。GRAAL算法通过蛋白质网络的拓扑性质推算出2个网络中结点对的相似得分。在得到比对结点对的相似得分后,使用贪婪算法或者匈牙利算法进行搜索。
2.2.2 基于图拓扑结构网络结构比对方法的特点1)建立比对图,通过整合网络中结点和结点之间的相互作用的相关数据,构造出网络结构比对的二分图。
2)定义结点相似得分函数,依据复杂网络的特性,设计出网络的结点的相似得分比较方法,将网络结构比对问题转化为求解比对图的问题。
3)设计搜索算法,在众多启发式算法中选择一种适合待比对图特性的搜索算法。完成结点对的比对问题。与基于数学框架网络结构比对方法不同,不需要把比对结果还原到原来的网络中。这种方法得到的对比对结果会直接的反映到比对图上。直接得到最大权重比对子图[51]。
2.3 网络结构比对的其他算法NSD算法[52]是一种结合相似得分计算的“拆开”(输入数据的独立的预处理)和“分解”的排名的网络结构比对问题。DNS方法优点是可以快速计算网络拓扑中的结点相似性,并且这种方法可以比对任何拓扑网络。它的参数和输出处理都可以为特定的比对问题而变化。腔算法[18]是一种分布式算法。他可以有效地处理全局拓扑约束下优化问题。交互概率[7]网络结构比对方法是通过概率生成函数来有效地在复杂网络中计算结点度分布。Corbi算法[53]通过采取迭代的双向映射的方法进行网络结构比对。它在比对过程中考虑进化事件,包括结点的插入与删除、边缘的连接与分离。并且这种方法从匹配的结点数目、边缘正确率、边缘覆盖率和最大的共同的连通子图的大小等方面分析网络比较结果的好坏。文献[54]介绍了一种通过e3模型[55]进行网络结构比对的一种方法。e3算法的目标是在有限的时间步数内收敛到一个近似最优结果。该文献介绍了e3模型在比对business-ICT网络上的应用,e3模型算法创造了在组织比对情况下使用多种结点进行比对,不仅仅限制在一种结点比对上。离散的粒子群优化算法[9]是一种可以部署目标函数的一种优化启发。
3 复杂网络结构比对存在的问题复杂网络结构比对问题是对数学、信息学、计算机科学和真实网络的相关知识的综合交叉领域的研究。例如,近几年在网络结构比对问题上热门的生物网络结构比对问题,就需要有相关的生物知识作为重要的理论支撑,需要清楚在生物网络结构比对过程中哪些信息对比对的结果至关重要,研究哪些组合优化算法和生物网络中的哪些特殊性会对这个特定的网络有更好的比对结果。当然在对这些信息研究的同时,需要有数学方法、信息学的基础理论和计算机等相关的学科知识作为基础。需要数学的思想方法和工具为各种学科做基础,需要信息学的理论对相关数据进行信息分析和处理,需要用计算机科学作为数据承载、处理和呈现的介质。在此,在复杂网络结构比对研究中对数据的预处理、结点相似性、结果评估问题这3个亟需解决的问题进行分析。
1)复杂网络数据的预处理问题
随着各种网络数据的快速增长,对数据的提取和处理也就成了一个既重要又困难的事情。对于生物网络这种特殊的网络来说,数据的提取就是一件复杂的事情,因为生物网络数据的来源是生物数据库,但这些数据库不仅仅有结点和相互作用关系的数据,还存在数据的来源、实验的方法等具体的信息,如何从数据库中提取感兴趣的数据是很重要的。也可以将网络数据抽象为图,将实验数据中的网络数据信息转换成图中顶点和边上的属性。
数据的预处理就更加困难,由于数据本身的具有的大量性和噪声性。如何建立高可信度的模型是需要解决的问题。对于网络数据的处理来说,现在主要有2个处理方向,一个方向是通过计算分析技术来评估和排名[56, 57]网络数据中相互作用关系的可靠性。这种方法主要是通过对相互作用的网络数据的局部分析和全局分析来监测数据。局部分析通过是否有共同的定位数据或有共同作用的数据的这2个条件判断这组数据是否可靠。文献[58, 59]通过对数据来源可靠性的判断微调局部分析的结果。经典网络比对方法[41, 60]通过给复杂网络中的相互作用数据赋一个权重来说明数据的可信度。文献[60]使用多种数据源建模可信数据。这种方法的不足是在处理稀疏矩阵[61]的时候,它的效果会急剧下降。
据建模成欧几里得空间的点集合[62],这种方法主要是先设定距离参数ε,如果2点之间的距离小于ε,就可以表示这2点之间的相互作用是可靠的。这种方法也是近几年的一种趋势。文献[63, 64]介绍了一种非凸语义嵌入的方法,在相互作用数据中使用自适应欧几里得嵌入方法,这种在欧几里得空间中求距离的方法适用于紧密相连的数据库和系数的数据库。但是以上的方法对假阴性数据的检测是十分困难的,因为检测假阴性数据可靠性等同于对预测新的相互作用关系。处理后的数据依然存在一定比例的假阴性与假阳性,如何提高处理数据的能力也是接下来要着重解决的问题。
2)结点的相似性范围计算问题
结点的相似性计算是网络结构比对的基础,在基于数学框架网络结构比对方法中,相似性是定义整数二次规划和矩阵特征值公式的基础,在基于图拓扑结构网络结构比对算法中,结点的相似性计算,是网络结构比对的核心问题,只有在结点的相似性已知的前提才可进行启发式的搜索算法寻找最大公共子图。经典算法Graemlin2.0[42]在网络数据的序列数据和拓扑结构相似数据的基础上将功能相似性引入到相似度函数定义中。但是在得到结点的相似得分之后,如何确定匹配结点的相似得分范围是一个需要深入分析的问题。MHA[43]方法通过ProportionalHill[44]算法预测功能模块的范围,但是这种方法获得数据的准确率不是很高,其次确定相似得分范围的方法都通过对特定的网络进行大量的实验,验证什么范围内的结点会有更好的比对结果。这种方法需要大量的工作量,因为就算是对同一种类型网络的进行比对,不同的网络结点匹配的相似性范围也是不同的。如何使网络的比对算法自动地确定匹配的相似得分范围是当前要解决的问题之一。
3)复杂网络结构比对结果评估问题
现在没有一种标准规范来评价网络结构比对的结果。现在对网络结构比对结果的评估主要是在比对算法的执行效率方面和运行结果方面估。对网络结构比对的结果评估首先建立一组和原有网络一致的随机网络并在上面运行比对算法,基于随机网络上的比对结果和真实网络上的比对结果设定评价标准,得到评价函数,解释算法统计的显著性。但是对网络结构比对结果的实际应用性方面分析,却没有统一的标准。例如在生物网络结构比对结果的中得到了相对应的结点,但最终匹配的结点的正确率却没有被实际的统计过。算法Graemlin2.0[42]是第1个方法提出网络比对评价的基准,它将自己的方法与NetworkBLAST[38]、MaWISH[40]、IsoRank[13]以及Grmlin[41]等4种方法进行了量化评测。HopeMap[24]算法提出一个通用的评分系统,这个方法提出将网络比对的结果和多种数据注释方法进行比较,得到一个较为通用的正确率。从网络匹配的正确率这方面来说这就需要生物相关的技术与计算机技术相协作,最终提高网络结构比对的实用性。复杂的网络结构比对方法还在进一步研究中,但是增大比对网络的范围和设计更有效的结果分析方案是必要的。
4 结束语通过改进和完善复杂网络比对方法,把这种方法应用到各种规模各种形式上的网络数据中,比对具体的网络数据来解决实际问题。除了现在普遍使用的启发式方法和线性规划方法,其他的解决方案可能也会有更好的比对效果,例如结合参数化方法,值得人们深入研究。
复杂网络结构比对是近年来研究热点之一,考虑到复杂网络的模块性和实际网络的动态性,复杂网络结构比对算法发展的主要发展趋向3个方面:
1)识别重叠的网络结构比对部分。现在算法对于结点映射关系是一一对应的,但在现实的很多网络中结点是具有重叠性,例如生物网络中的进化模块,很多结点都是重叠的。所以在未来的网络结构比对算法要释放网络结点比对一对的一映射的限制。模糊聚类法[65, 66]和中心发现法[67]都可以用来识别重叠模块
2)构建动态的网络结构比对模型。随着对复杂网络的深入研究,现在已经有很多算法对复杂网络进行动态性研究[68]。动态性研究提高了对复杂网络的认识,把网络的动态研究扩展到构建动态网络结构比对模型的应用上是十分重要的,现在已经有一些动态网络研究的成果[69, 70]。
3)联系具体网络的属性,进行具有特定性的网络结构比对研究。例如对生物网络的比对,就需要在生物网络中结点以及相互作用所具有的生物属性[71],例如生物网络的结点具有保守性和进化性。
今后需要面对的挑战是,如何对这些数据进行预处理,把它们变成高质量的网络;如何集成并归集多个信息源将数据;如何提高网络结构比对的精度;如何依据具体的网络数据的不同性质的网络结构的比对来解决实际问题。
| [1] | STELZL U, WORM U, LALOWSKI M, et al. A human protein-protein interaction network: a resource for annotating the proteome[J]. Cell, 2005, 122 (6): 957-968. |
| [2] | REN B, ROBERT F, WYRICK J J, et al. Genome-wide location and function of DNA binding proteins[J]. Science, 2000, 290 (5500): 2306-2309. |
| [3] | MICHOEL T, NACHTERGAELE B. Alignment and integration of complex networks by hypergraph-based spectral clustering[J]. Physical Review E, 2012, 86 (5): 056111. |
| [4] | ERDO S P, R NYI A. On the evolution of random graphs[J]. American Mathematical Society, 1960, 517-561. |
| [5] | BONNICI V, GIUGNO R, PULVIRENTI A, et al. A subgraph isomorphism algorithm and its application to biochemical data[J]. BMC bioinformatics, 2013, 14 (Suppl 7): S13. |
| [6] | KHAN A M, GLEICH D F, POTHEN A, et al. A multithreaded algorithm for network alignment via approximate matching[C]//2012 International Conference on proceedings of the High Performance Computing, Networking, Storage and Analysis (SC). 2012. |
| [7] | TODOR A, DOBRA A, KAHVECI T. Probabilistic biological network alignment[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB), 2013, 10 (1): 109-121. |
| [8] | SHVAIKO P, EUZENAT J. Ontology matching: state of the art and future challenges[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25 (1): 158-176. |
| [9] | BOCK J, HETTENHAUSEN J. Discrete particle swarm optimisation for ontology alignment[J]. Information Sciences, 2012, 192: 152-173. |
| [10] | HU W, JIAN N, QU Y, et al. Gmo: a graph matching for ontologies[C]//proceedings of the Proceedings of K-CAP Workshop on Integrating Ontologies. 2005: 42-48. |
| [11] | MELNIK S, GARCIA-MOLINA H, RAHM E. Similarity flooding: a versatile graph matching algorithm and its application to schema matching[C]//Proceedings of the Proc 18th ICDE Conf(Best Student Paper award). 2002. |
| [12] | KLAU G W. A new graph-based method for pairwise global network alignment[J]. BMC bioinformatics, 2009, 10(Suppl 1): S59. |
| [13] | SINGH R, XU J, BERGER B. Pairwise global alignment of protein interaction networks by matching neighborhood topology[J]. 2007: 16-31. |
| [14] | SINGH R, XU J, BERGER B. Global alignment of multiple protein interaction networks with application to functional orthology detection[J]. Proceedings of the National Academy of Sciences, 2008, 105 (35): 12763-12768. |
| [15] | LAWLER E L. The quadratic assignment problem[J]. Management Science, 1963, 9 (4): 586-599. |
| [16] | MISENER R, FLOUDAS C A. GloMIQO: Global mixed-integer quadratic optimizer[J]. Journal of Global Optimization, 2012, 57 (1): |
| [17] | RIECK J, ZIMMERMANN J, GATHER T. Mixed-integer linear programming for resource leveling problems[J]. European Journal of Operational Research, 2012, 221 (1): 27-37. |
| [18] | BRADDE S, BRAUNSTEIN A, MAHMOUDI H, et al. Aligning graphs and finding substructures by a cavity approach[J]. EPL (Europhysics Letters), 2010, 89 (3): 37009. |
| [19] | BAYATI M, GERRITSEN M, GLEICH D F, et al. Algorithms for large, sparse network alignment problems[J]. 2009, 705-710. |
| [20] | EL-KEBIR M, HERINGA J, KLAU G W. Lagrangian relaxation applied to sparse global network alignment[M]. Springer. 2011: 225-236. |
| [21] | GUIGNARD M, KIM S. Lagrangean decomposition: a model yielding stronger Lagrangean bounds[J]. Mathematical Programming, 1987, 39 (2): 215-228. |
| [22] | SINGH R, XU J, BERGER B. Global alignment of multiple protein interaction networks with application to functional orthology detection[J]. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105 (35): 12763-12768. |
| [23] | KECECIOGLU J. The maximum weight trace problem in multiple sequence alignment[C]//proceedings of the Combinatorial pattern matching. Springer.1993: 106-119. |
| [24] | SAMATOVA N F. Global alignment of pairwise protein interaction networks for maximal common conserved patterns[J]. International Journal of Genomics, 2013: 670623. |
| [25] | BAUER M, KLAU G W, REINERT K, et al. Accurate multiple sequence-structure alignment of RNA sequences[J]. BMC Bioinformatics, 2009: 15-33. |
| [26] | BAYATI M, SHAH D, SHARMA M. Max-product for maximum weight matching: convergence, correctness, and LP duality[J]. IEEE Transactions on Information Theory, 2008, 54 (3): 1241-1251. |
| [27] | BAYATI M, GERRITSEN M, GLEICH D F, et al.Algorithms for large, sparse network alignment problems[C] //09 Ninth IEEE International Conference on proceedings of the Data Mining, 2009: 705-710. |
| [28] | PEARL J. Reverend Bayes on inference engines: a distributed hierarchical approach[C] //proceedings of the AAAI.1982: 133-136. |
| [29] | SANGHAVI S, MALIOUTOV D M, WILLSKY A S. Linear programming analysis of loopy belief propagation for weighted matching[C]//proceedings of the NIPS, 2007:. |
| [30] | DAGUM L, MENON R. OpenMP: an industry standard API for shared-memory programming[J]. IEEE Transactions on Computational Science & Engineering, 1998, 5 (1): 46-55. |
| [31] | JUNG J, MORI T, SUGITA Y. Midpoint cell method for hybrid (MPI+OpenMP) parallelization of molecular dynamics simulations[J]. Journal of computational chemistry, 2014: 1064-1072. |
| [32] | THOMAN P, JORDAN H, PELLEGRINI S, et al. Automatic OpenMP loop scheduling: a combined compiler and runtime approach[M]. Springer, 2012: 88-101. |
| [33] | GOUVEIA A, SILVA N, ROCHA J, et al. Iterative ontology alignment debugging using a scenario-and strategy-driven approach[C]// International Workshop on proceedings of the Database and Expert Systems Applications (DEXA), 2012\: 254-258. |
| [34] | PAGE L, BRIN S, MOTWANI R, et al. The PageRank citation ranking: bringing order to the web[J]. 1999: 102-109. |
| [35] | LIAO C-S, LU K, BAYM M, et al. IsoRankN: spectral methods for global alignment of multiple protein networks[J]. Bioinformatics, 2009, 25 (12): i253-i258. |
| [36] | ANDERSEN R, CHUNG F, LANG K. Local graph partitioning using pagerank vectors[C]//47th Annual IEEE Symposium on proceedings of the Foundations of Computer Science, 2006 2006:. |
| [37] | ALADAG A E, ERTEN C. SPINAL: scalable protein interaction network alignment[J]. Bioinformatics, 2013, 29 (7): 917-924. |
| [38] | KELLEY B P, YUAN B, LEWITTER F, et al. PathBLAST: a tool for alignment of protein interaction networks[J]. Nucleic acids research, 2004, 32 (suppl 2): W83-W88. |
| [39] | SHARAN R, SUTHRAM S, KELLEY R M, et al. Conserved patterns of protein interaction in multiple species[J]. Proceedings of the National Academy of Sciences of the United States of America, 2005, 102 (6): 1974-1979. |
| [40] | KOYUT RK M, KIM Y, TOPKARA U, et al. Pairwise alignment of protein interaction networks[J]. Journal of Computational Biology, 2006, 13 (2): 182-199. |
| [41] | FLANNICK J, NOVAK A, SRINIVASAN B S, et al. Graemlin: general and robust alignment of multiple large interaction networks[J]. Genome Research, 2006, 16 (9): 1169-1181. |
| [42] | FLANNICK J, NOVAK A, DO C B, et al.Automatic parameter learning for multiple network alignment[C] //Proceedings of the Research in Computational Molecular Biology, F, 2008: 214-231. |
| [43] | WANG B, GAO L. Seed selection strategy in global network alignment without destroying the entire structures of functional modules[J]. Proteome science, 2012, 10 (Suppl 1): S16. |
| [44] | KOV CS I A, PALOTAI R, SZALAY M S, et al. Community landscapes: an integrative approach to determine overlapping network module hierarchy, identify key nodes and predict network dynamics[J]. PloS one, 2010, 5 (9): e12528. |
| [45] | MILENKOVIC T, ADVISER-PRZULJ N. From topological network analyses and alignments to biological function, disease, and evolution[M]. California State University at Long Beach, 2010 |
| [46] | ATIAS N, SHARAN R. Comparative analysis of protein networks: hard problems, practical solutions[J]. Communications of the ACM, 2012, 55 (5): 88-97. |
| [47] | MILENKOVI C T, PRZULJ N. Uncovering biological network function via graphlet degree signatures[J]. Cancer informatics, 2008, (6): 56-65. |
| [48] | MILLS-TETTEY G A, STENTZ A, DIAS M B. The dynamic hungarian algorithm for the assignment problem with changing costs[J]. 2007: 1-19. |
| [49] | WEST D B. Introduction to graph theory[M]. Prentice hall Upper Saddle River, 2001: 178-185. |
| [50] | MEMIŠEVIC V, PRZULJ N. C-GRAAL: Common-neighbors-based global GRAph ALignment of biological networks[J]. Integrative Biology, 2012, 4 (7): 734-743. |
| [51] | DUAN R, PETTIE S. Linear-Time Approximation for Maximum Weight Matching[J]. Journal of the ACM (JACM), 2014, 61 (1): 1. |
| [52] | KOLLIAS G, MOHAMMADI S, GRAMA A. Network Similarity Decomposition (NSD): A fast and scalable approach to network alignment[J]. Knowledge and Data Engineering, IEEE Transactions on, 2012, 24 (12): 2232-2243. |
| [53] | HUANG Q, WU L-Y, ZHANG X-S. Corbi: A new R package for biological network alignment and querying[J]. BMC Systems Biology, 2013, 7 (2): 1-9. |
| [54] | PIJPERS V, DE LEENHEER P, GORDIJN J, et al. Using conceptual models to explore business-ICT alignment in networked value constellations[J]. Requirements Engineering, 2012, 17 (3): 203-226. |
| [55] | KEARNS M, SINGH S. Near-optimal reinforcement learning in polynomial time[J]. Machine Learning, 2002, 49 (2-3): 209-232. |
| [56] | LIU G, LI J, WONG L. Assessing and predicting protein interactions using both local and global network topological metrics[J]. Genome Informatics, 2008, 22 138-149. |
| [57] | KUCHAIEV O, RAŠAJSKI M, HIGHAM D J, et al. Geometric de-noising of protein-protein interaction networks[J]. PLoS computational biology, 2009, 5 (8): e1000454. |
| [58] | CHUA H N, SUNG W-K, WONG L. Exploiting indirect neighbours and topological weight to predict protein function from protein-protein interactions[J]. Bioinformatics, 2006, 22 (13): 1623-1630. |
| [59] | NABIEVA E, JIM K, AGARWAL A, et al. Whole-proteome prediction of protein function via graph-theoretic analysis of interaction maps[J]. Bioinformatics, 2005, 21 (suppl 1): i302-i310. |
| [60] | ALI W, DEANE C M. Functionally guided alignment of protein interaction networks for module detection[J]. Bioinformatics, 2009, 25 (23): 3166-3173. |
| [61] | CLAUSET A, MOORE C, NEWMAN M E. Hierarchical structure and the prediction of missing links in networks[J]. Nature, 2008, 453 (7191): 98-101. |
| [62] | PRŽULJ N. Biological network comparison using graphlet degree distribution[J]. Bioinformatics, 2007, 23 (2): e177-e183. |
| [63] | ZHU L, YOU Z-H, HUANG D-S. Increasing the reliability of protein-protein interaction networks via non-convex semantic embedding[J]. Neurocomputing, 2013, v121, p99-107. |
| [64] | TERRADOT L, DURNELL N, LI M, et al. Biochemical Characterization of Protein Complexes from the Helicobacter pylori Protein Interaction Map Strategies for Complex Formation and Evidence for Novel Interactions Within Type IV Secretion Systems[J]. Molecular & Cellular Proteomics, 2004, 3 (8): 809-819. |
| [65] | SUN P G, GAO L, SHAN HAN S. Identification of overlapping and non-overlapping community structure by fuzzy clustering in complex networks[J]. Information Sciences, 2011, 181 (6): 1060-1071. |
| [66] | HAVEMANN F, GL SER J, HEINZ M, et al. Identifying overlapping and hierarchical thematic structures in networks of scholarly papers: A comparison of three approaches[J]. PloS one, 2012, 7 (3): e33255. |
| [67] | LEE C, REID F, MCDAID A, et al. Seeding for pervasively overlapping communities[J]. Physical Review E, 2011, 83 (6). |
| [68] | DENT J E, YANG X, NARDINI C. SPNConverter: a new link between static and dynamic complex network analysis[J]. Bioinformatics, 2013, 29 (19): 2507-2508. |
| [69] | WANG J, PENG X, PENG W, et al. Dynamic protein interaction network construction and applications[J]. Proteomics, 2014, 14 (4-5): 338-352. |
| [70] | VAN DEN HOF P M, DANKERS A, HEUBERGER P S, et al. Identification of dynamic models in complex networks with prediction error methods—Basic methods for consistent module estimates[J]. Automatica, 2013, 49 (10): 2994-3006. |
| [71] | MA'AYAN A. Insights into the organization of biochemical regulatory networks using graph theory analyses[J]. Journal of biological chemistry, 2009, 284 (9): 5451-5455. |



