2. Department of Scientific Research, Naval Aeronautical and Astronautical University, Yantai 264001, China
人工免疫系统(artificial immune system,AIS)起源于20世纪80年代末90年代初,是基于免疫系统机制和理论免疫学而发展的各种人工范例的统称[1]。人工免疫系统的免疫智能算法主要包括否定选择算法、克隆选择算法和免疫网络算法等[2, 3, 4]。
否定选择算法(negative selection algorithm,NSA)是在1994年由美国学者Forrest等首先提出的,该算法借鉴免疫系统的自己-非己识别原理,模拟免疫细胞的成熟过程,删除那些对自己产生应答的免疫细胞,从而实现了自体耐受[5, 6]。否定选择算法的目标是产生足够多的非己空间检测器,因此检测器的表示和匹配规则就成为决定否定选择算法性能的重要因素。目前检测器的表示方法主要有二进制表示和实值表示2种。针对不同的表示方法,匹配规则主要有r毗邻匹配(rcb)、r块匹配(r-chunk)、Hamming距离和Euclidean距离等[7, 8]。二进制表示能够很好模拟免疫系统的多样性和动态性,便于计算机的存储和计算,但知识表达能力较差,尤其在解决多维问题中不利于问题描述,计算量过大;实值表示可将现实问题与实值空间一一对应,用实向量表达各种物理状态,直观简洁,但是无法描述每个物理状态的属性变化范围。
可拓学是由我国学者蔡文教授于1983年提出,其核心是基元理论、可拓集理论和可拓逻辑[9]。采用基元表示检测器,不仅可以直观地描述多维物理量的属性变化范围,而且能够方便地使用关联函数作为匹配规则,对检测器的匹配结果给出定量的描述。已有学者将可拓学与人工免疫系统相结合,文献[10]将免疫网络算法引入可拓控制理论用于关联函数经典域的优化,文献[11]将免疫系统的学习机制和否定选择机制与可拓学中的优度评价方法相结合进行汽轮机的故障诊断,本文将在前人研究成果的基础上,进一步研究可拓否定选择算法及其在故障诊断中的应用。
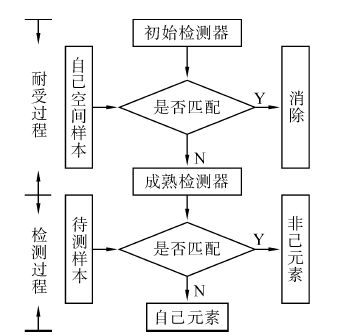
1 否定选择原理否定选择包括耐受和检测2个阶段,耐受阶段模拟T细胞在胸腺的检查过程,负责成熟检测器的生成;检测阶段模拟T细胞的非己识别过程,负责抗原的检测[12]。否定选择原理如图 1所示。 耐受过程:针对检测器产生机制生成大量初始检测器,把其中不与自己空间样本匹配的初始检测器设置为成熟检测器,且把发生匹配的初始检测器清除。 检测过程:将待测样本与成熟检测器逐个比较,如果出现匹配则证明为非己空间元素,否则为自己空间元素。
|
| 图 1 否定选择算法原理 Fig. 1 Principle of negative selection algorithm |
用基元描述问题空间、检测器和样本数据,并使用关联函数作为检测器匹配规则的基础,形成了可拓否定选择算法。
2.1 模型的基元描述在否定选择算法中,首先要准确定义问题空间,借鉴Gonzalez在文献[13]中的做法,把问题空间归一化为超矩形空间[0,1]n,不同的是本文用基元进行表示,假设超矩形n维空间上的n个特征向量分别是x1,x2,…,xn,则问题空间用基元表示为
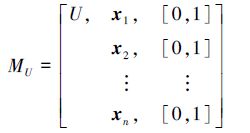
问题空间中包括自己空间Us和非己空间Uns两部分,且Us∪Uns=U,Us∩Uns=∅。
检测器d是问题空间中的一个小超矩形,用基元表示为
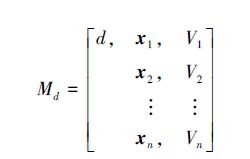
检测器d对应特征向量xi(i=1,2,…,n)的属性范围是Vi=[viL,viH]。viL和viH分别表示检测器在特征向量xi方向上能够检测的最小值和最大值,则检测器d在整个问题空间中能够覆盖的范围是

问题空间中的任意一个样本s,s∈U用基元表示为

采用基元表示样本和检测器后,就可以用关联函数表示亲和度,对于问题空间的每个特征向量xi,样本s的属性值vi关于特征向量范围V=[0,1]和检测器d对应特征向量的属性范围Vi=[viL,viH]的关联函数k(vi)为如下。
当ρ(vi,Vi)=ρ(vi,V)且v∉Vi时,
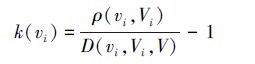
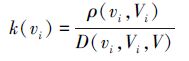
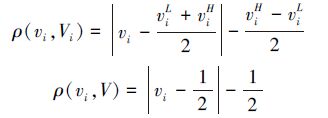
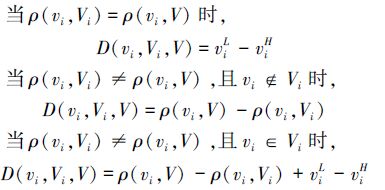
根据关联函数的性质,可知当vi∈Vi时,1>k(vi)≥0,即点vi在区间Vi内;当vi∉Vi,vi∈V时,0>k(vi)≥-1,即点vi在区间Vi外,但在区间V内。
定义样本s和检测器d关于特征向量xi的亲和度为
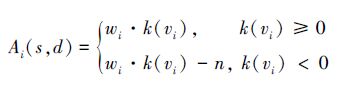
 ,wi≥0,i=1,2,…,n。
,wi≥0,i=1,2,…,n。
则样本s和检测器d的综合亲和度为
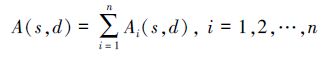
目前在否定选择算法中应用的检测器生成算法主要有穷举法、线性法和贪心法[14]。穷举检测器生成法的耗时较长,在一定检测率下,候选检测器的个数和自己空间元素的个数成指数关系;线性检测器生成算法的耗时与检测器个数和自己空间元素个数成线性关系,但生成检测器有冗余;贪心检测器生成算法可消除检测器冗余,但不能使检测器生成时间最小化。为此提出可拓检测器生成算法,该算法的基本思想是将问题空间分割成m个小超矩形将其视为m个检测器与自己空间中的元素进行匹配,如果亲和度A(s,d)小于某个阈值δ,则将其记为成熟检测器,如果亲和度大于阈值δ,则对该检测器进行进一步分割,并用分割后的检测器重新对自己空间中的元素进行匹配,重复这一过程直到达到指定的分割级数c或者分割精度p,得到的所有检测器即为初始检测器集。
可拓检测器生成算法的具体步骤为:
1)初始化问题空间U,自己空间Us,将整个问题空间看成是一个未成熟检测器dy,此时分割级数c=1;
2)对未成熟检测器dy进行分割,得到检测器d1,d2,…,dm;
3)对得到的每一个检测器di,i=1,2,…,m,计算其与所有自己空间样本的亲和度A(s,d),如果对于任意s∈Us,都满足A(s,d)<δ,则将此检测器记为成熟检测器dmj,j=1,2,…,m1,否则记为未成熟检测器dyk,k=1,2,…,m2,且m1+m2=m。
4)判断分割级数c是否达到要求,如果是算法结束,否则分割级数c=c+1,对得到的每一个未成熟检测器dyk,k=1,2,…,m2,返回步骤2)。
2.3 检测器优化算法通过对提出的可拓检测器生成算法的分析可知,得到的成熟检测器不存在冗余,但需要对得到成熟检测器进行优化,即对特征向量属性范围相邻的检测器进行合并,从而减少检测器的数目。为此提出可拓检测器优化算法,该算法的基本思想是将问题空间按最大分割级数c或者最小分割精度p进行分割,得到m个检测器d1,d2,…,dm,如果成熟检测器集中存在dm,使得A(di,dm)>0,则记为成熟检测器dmj,j=1,2,…,m1,否则记为未成熟检测器dyk,k=1,2,…,m2,且m1+m2=m。对得到的最小单元成熟检测器,按照一定的原则进行合并,直到所有的成熟检测器都无法合并为止,即可得到优化后的检测器。需要说明的是合并原则并不惟一,这里只给出其中一种。
原则1 根据检测器生成时的标号顺序进行检测器的合并。
原则2 对于某一检测器优先考虑和基于第1个特征向量的检测器合并,再考虑与基于第2个特征向量的检测器合并,高维情况以此类推。
针对本文给出的合并原则,给出可拓检测器优化算法的具体步骤为:
1)对整个问题空间按照最大分割级数c进行最小单元分割,得到m个检测器d1,d2,…,dm;
2)对得到的每一个检测器di,i=1,2,…,m,如果存在成熟检测器dm,使得A(di,dm)>0,则记为成熟检测器dmj,j=1,2,…,m1,否则记为未成熟检测器dyk,k=1,2,…,m2,且m1+m2=m。
3)按照检测器标号的顺序,依此在特征向量x1,x2,…,xn的方向上对检测器进行合并,得到合并后的成熟检测器dmj,j=1,2,…,m′1。 4)重复步骤3)直到所有成熟检测器都无法合并为止。
2.4 参数分析首先定义成熟检测器集在问题空间中的覆盖率pc和检测率pd,然后重点讨论阈值δ的变化对检测器覆盖率pc和检测率pd的影响。
假设对问题空间按最大分割级数c或者最小分割精度p进行分割后,得到最小单元检测器m个,其中成熟检测器m1个,未成熟检测器m-m1个,则成熟检测器集在整个问题空间中的覆盖率为pc=m1/m。若该问题空间中共包含t个样本,其中在成熟检测器覆盖范围内的有t1个,则成熟检测器集在整个问题空间中的检测率为pd=t1t。
在可拓否定选择算法的不同阶段,阈值δ的取值对覆盖率pc和检测率pd的影响不同。在耐受过程中,增大阈值δ,使得δ≥0,则可忽略检测器内边界附近的自己空间元素,可能会造成成熟检测器数量增多,覆盖率pc增加,反之可能会造成覆盖率pc减小;在检测过程中,减小阈值δ,使得δ≤0,则检测器外边界附近的抗体仍可被检测,可能会造成单个检测器的覆盖范围增加,涵盖的非己空间元素增多,检测率pd增加,反之可能会造成检测率pd减小。所以应在可拓否定选择算法的耐受阶段取阈值δ≥0,而在检测阶段取阈值δ≤0。
3 应用实例故障数据贫瘠一直是故障诊断领域难以解决的一项难题[15],而可拓否定选择算法恰恰不需要故障数据,仅通过被测对象的正常状态数据,就可以进行故障检测,所以将可拓否定选择算法应用到故障诊断领域十分合适。
以某型飞机综合显控平台的测试数据为例,采用可拓否定选择算法进行故障检测。首先对测试数据进行分析,在综合显控平台的测试过程中,一共测试了54个指标,由于指标间存在相关性,因此通过相关性分析选取了其中的6个指标作为问题空间的特征向量xi,i=1,2,…,6。选取20组正常状态的测试数据用于可拓否定选择算法的耐受过程,另取10组测试数据用于检测过程。
1)测试数据标准化。
用极差变换公式对特征向量进行标准化,以消除不同量纲的影响,并使所有的特征值统一于共同的数值区间[0,1],即将问题空间转换为[0,1]n,这样不仅便于算法实现,同时避免由于某一维数据过小,而使其特征参数作用被弱化。极差变换公式为
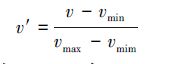
当v=vmin时,v′=0;当v=vmax时,v′=1。vmin和vmax是根据测试需求确定的,当测量值v>vmax或者v<vmin时,表示被测对象故障,当vmax≥v≥vmin时,无法直接判断被测对象是否故障,需要使用算法进行故障检测,标准化后的测试数据,见表 1。前20组是正常状态数据用于生成成熟检测器,后10组数据中包含故障数据和正常数据各5组,用于故障检测。
| 序号 | v1 | v2 | v3 | v4 | v5 | v6 | 状态 |
| 1 | 0.538 | 0.870 | 0.295 | 0.308 | 0.318 | 0.670 | 正常 |
| 2 | 0.537 | 0.885 | 0.303 | 0.315 | 0.334 | 0.670 | 正常 |
| 3 | 0.537 | 0.845 | 0.305 | 0.313 | 0.322 | 0.670 | 正常 |
| 4 | 0.514 | 0.975 | 0.295 | 0.280 | 0.188 | 0.670 | 正常 |
| 5 | 0.540 | 0.535 | 0.435 | 0.363 | 0.496 | 0.700 | 正常 |
| 6 | 0.538 | 0.720 | 0.395 | 0.360 | 0.484 | 0.700 | 正常 |
| 7 | 0.538 | 0.965 | 0.288 | 0.310 | 0.328 | 0.670 | 正常 |
| 8 | 0.540 | 0.850 | 0.300 | 0.310 | 0.320 | 0.670 | 正常 |
| 9 | 0.519 | 0.765 | 0.488 | 0.385 | 0.574 | 0.710 | 正常 |
| 10 | 0.542 | 0.555 | 0.413 | 0.370 | 0.512 | 0.705 | 正常 |
| 11 | 0.546 | 0.940 | 0.470 | 0.365 | 0.508 | 0.700 | 正常 |
| 12 | 0.523 | 0.630 | 0.435 | 0.455 | 0.812 | 0.760 | 正常 |
| 13 | 0.536 | 0.945 | 0.498 | 0.373 | 0.524 | 0.705 | 正常 |
| 14 | 0.519 | 0.780 | 0.465 | 0.380 | 0.554 | 0.710 | 正常 |
| 15 | 0.539 | 0.540 | 0.390 | 0.375 | 0.534 | 0.710 | 正常 |
| 16 | 0.517 | 0.780 | 0.615 | 0.350 | 0.452 | 0.690 | 正常 |
| 17 | 0.539 | 0.545 | 0.608 | 0.370 | 0.510 | 0.705 | 正常 |
| 18 | 0.509 | 0.770 | 0.625 | 0.370 | 0.528 | 0.705 | 正常 |
| 19 | 0.536 | 0.515 | 0.613 | 0.428 | 0.710 | 0.740 | 正常 |
| 20 | 0.534 | 0.510 | 0.610 | 0.428 | 0.710 | 0.740 | 正常 |
| 21 | 0.481 | 0.475 | 0.610 | 0.363 | 0.502 | 0.705 | 故障 |
| 22 | 0.189 | 0.555 | 0.615 | 0.385 | 0.586 | 0.715 | 故障 |
| 23 | 0.410 | 0.575 | 0.613 | 0.365 | 0.510 | 0.705 | 故障 |
| 24 | 0.538 | 1.420 | 0.293 | 0.305 | 0.302 | 0.670 | 故障 |
| 25 | 0.515 | 0.475 | 0.610 | 0.440 | 0.756 | 0.745 | 故障 |
| 26 | 0.517 | 0.770 | 0.293 | 0.330 | 0.388 | 0.685 | 正常 |
| 27 | 0.540 | 0.770 | 0.295 | 0.315 | 0.338 | 0.675 | 正常 |
| 28 | 0.517 | 0.750 | 0.298 | 0.310 | 0.316 | 0.670 | 正常 |
| 29 | 0.518 | 0.735 | 0.300 | 0.310 | 0.320 | 0.670 | 正常 |
| 30 | 0.540 | 0.760 | 0.300 | 0.318 | 0.344 | 0.675 | 正常 |
2)检测器生成。
代入前20组正常状态测试数据,应用可拓检测器生成算法得到成熟检测器,取阈值δ=0,且6个特征向量等权重,经过1级分割后得到64个检测器,通过与20个自己空间元素进行匹配,得到4个未成熟检测器和60个成熟检测器,由于已经达到分割精度要求,所以算法结束。
3)检测器优化。
采用可拓检测器优化算法对得到的60个成熟检测器进行优化,得到4个成熟检测器,每个检测器的特征向量属性范围,见表 2。 o2
| 序号 | d1 | d2 | d3 | d4 |
| V1 | [0,0.5] | [0.5,1] | [0.5,1] | [0.5,1] |
| V2 | [0,1] | [0,0.5] | [0.5,1] | [0.5,1] |
| V3 | [0,1] | [0,1] | [0,1] | [0,1] |
| V4 | [0,1] | [0,1] | [0.5,1] | [0,0.5] |
| V5 | [0,1] | [0,1] | [0,1] | [0,1] |
| V6 | [0,1] | [0,1] | [0,1] | [0,0.5] |
4)抗原检测。
最后采用优化后的检测器对后10组测试数据进行故障检测,检测结果见表 3。
| 序号 | d1 | d2 | d3 | d4 | 状态 |
| 21 | 0.343 | -5.741 | -17.864 | -17.889 | 故障 |
| 22 | 0.382 | -11.877 | -11.943 | -11.985 | 故障 |
| 23 | 0.357 | -11.799 | -11.855 | -11.882 | 故障 |
| 24 | +∞ | -6.089 | +∞ | +∞ | 故障 |
| 25 | -5.704 | 0.235 | -11.875 | -11.959 | 故障 |
| 26 | -5.746 | -5.864 | -5.809 | -5.809 | 正常 |
| 27 | -5.763 | -5.864 | -5.812 | -5.801 | 正常 |
| 28 | -5.755 | -5.869 | -5.817 | -5.802 | 正常 |
| 29 | -5.752 | -5.863 | -5.821 | -5.806 | 正常 |
| 30 | -5.759 | -5.859 | -5.806 | -5.797 | 正常 |
表 3中显示的是10组测试数据与4个成熟检测器的综合亲和度。由诊断结果可知,21号、22号和23号故障数据可由d1检测;25号故障数据可由d2检测;24号故障数据可同时由d1、d3或d4检测,原因是24号数据的第2个特征向量值v2∉[0, 1],导致综合亲和度指标达到无穷大∞。其他数据为正常状态,检测结果完全正确。
检测器能够检测故障的数目与检测器的覆盖范围成正比,4个检测器的覆盖范围分别为Sd1=0.5,Sd2=0.25,Sd3=0.125和Sd4=0.062 5,所以检测器d1能够检测故障个数最多,与检测结果一致。
4 结束语将可拓学与否定选择算法相融合,提出了可拓否定选择算法,用于解决无故障样本条件下的故障检测问题。分别设计了可拓检测器生成和可拓检测器优化算法,使得检测器的覆盖范围大、数目少、且无冗余,最后采用某型飞机综合显控平台的测试数据进行算法验证,结果表明提出的可拓否定选择算法能够正确地区分正常状态数据和故障状态数据,具有较高的检测率,但可拓否定选择算法无法确定具体的故障模式,即无法实现故障隔离,这将是以后研究的方向。
| [1] | DASGUPTAA D, YUA S, NINO F. Recent advances in artificial immune system: models and application[J]. Applied Soft Computing, 2011, 11(2): 1574-1587. |
| [2] | 李红芳, 张清华, 谢克明. 一种新型免疫学习算法在故障诊断中的应用[J]. 智能系统学报, 2008, 3(5): 449-454.LI Hongfang, ZHANG Qinghua, XIE Keming. Application of a novel immune network learning algorithm to fault diagnosis[J]. CAAI Transactions on Intelligence Systems, 2008, 3(5): 449-454. |
| [3] | 刘勇, 尚永爽, 王怡苹. 基于免疫模型的故障诊断方法及应用[J]. 计算机工程, 2011, 37(16): 5-7.LI Yong, SHANG Yongshuang, WANG Yiping. Fault diagnosis method based on immune model and its application[J]. Computer Engineering, 2011, 37(16): 5-7. |
| [4] | CHEN Wen, LI Tao, LIU Xiaojie, et al. A negative selection algorithm based on hierarchical clustering of self set[J]. Science China: Information Sciences, 2013, 56(8): 1-13. |
| [5] | CHEN Guangzhu, ZHANG Lei, BAO Jiusheng. An improved negative selection algorithm and its application in the fault diagnosis of vibrating screen by wireless sensor networks[J]. Journal of Computational and Theoretical Nanoscience, 2013, 10(10): 2418-2426. |
| [6] | GAO X Z, WANG X, ZENGER K. Motor fault diagnosis using negative selection algorithm[J]. Journal of Computing and Application, 2014, 25(1): 55-65. |
| [7] | 金章赞, 廖明宏, 肖明. 否定选择算法综述[J]. 通信学报, 2013, 34(1): 159-170.JIN Zhangzan, LIAO Minghong, XIAO Ming. Survey of negative selection algorithms[J]. Journal on Communications, 2013,34(1):159-170. |
| [8] | GONZALEZ F, DASGUPTA D, GOMEZ J. The effect of binary matching rules in negative selection[C]//Proceedings of the Genetic and Evolutionary Computation Conference. Chicago, USA, 2003: 195-206. |
| [9] | 杨春燕, 蔡文. 可拓工程[M]. 北京: 科学出版社, 2010: 18-97. |
| [10] | 向长城. 基于免疫网络算法关联函数经典域优化[J]. 湖北民族学院学报:自然科学版, 2009, 27(4): 141-146.XIANG Changcheng. Classical fields optimum of independent function based on artificial immune network algorithm[J]. Journal of Hubei University for Nationalities: Natural Science Edition, 2009, 27(4): 141-146. |
| [11] | 向长城, 黄席樾. 可拓免疫算法在汽轮机故障诊断中的应用[J]. 四川大学学报:工程科学版, 2008, 40(2): 141-146.XIANG Changcheng, HUANG Xiyue. Application of extenics immunity algorithm to turbo generator fault diagnosis[J]. Jouranl of Sichuan University: Engineering Science, 2008, 40(2): 141-146. |
| [12] | GONZALEZ F, DASGUPTA D, NINO L F. A randomized real-valued negative selection algorithm[C]//Proceedings of the 2nd International Conference on Artificial Immune Systems. Edinburgh, UK, 2003: 261-272. |
| [13] | GONZALEZ F, DASGUPTA D, KOZMA R. Combining negative selection and classification techniques for anomaly detection[C]//Proceedings of the 2002 Congress on Evolutionary Computation. Honolulu, USA, 2002: 705-710. |
| [14] | AYARA M, TIMMIS J, De LEMOS R, et al. Negative selection: how to generate detectors[C]//Proceedings of 1st International Conference on Artificial Immune Systems. Canterbury, UK, 2002, 1: 89-98. |
| [15] | 徐学邈, 王如根, 侯胜利. 基于反面选择原理的智能融合故障检测模型及其应用[J]. 系统工程与电子技术, 2009, 31(8): 2029-2032.XU Xuemiao, WANG Rugen, HOU Shengli. Intelligence fusion approach to fault detection based on negative selection principle and its application[J]. Systems Engineering and Electronics, 2009, 31(8): 2029-2032. |



