日益现代化的交通方式给人们出行带来很大便利,其中公交与地铁是大型城市中的主要交通工具。考虑到我国人口众多,城市交通拥堵问题日益严重,对公交地铁系统的研究已成为一个热门又困难的课题。公交地铁系统的研究主要包括网络构建、公交配流与最优路选择算法3个方面,而查询算法在其中起到核心作用,它为人们提供出行的路径选择,切身关系到整个公交地铁网络是否高效运作,是公交系统研究的核心问题之一。
目前虽然有一系列针对公交网络的最短路径搜索算法[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],主要包括基于图论的查询算法[1, 9],基于数据库的查询算法[2, 5]和基于矩阵运算的查询算法[11]。目前针对地铁主导下的公交网络的最短路径搜索算法却不多见。
考虑到地铁在大城市公交系统中日益占主导地位这一事实,在文献[9]的基础上,将优选地铁出行作为基本出发点,对公交与地铁站点标号的同时,将地铁线路上站点间的权值成倍缩小,再依次按照换乘次数、乘车距离进行路径选择时就达到了优选地铁的目的,且一体化后的模型更加清晰、简便。
1 高维数组的表示称一个数组是k维的,如果它的元素是由k个指标索引的,更确切地说,称S是一个形如 Id(i1,i2,…,ik;n1,n2,…,nk)的k维数组,如果它能表示成[10, 12]:
S的大小,即S中元素的个数,记作|S|。且|S|=n1×n2×…×nk。
记σ(1),σ(2),…,σ(k)是1,2,…,k的一个排列,若它能排成一个
 形式排列的,即按照t-行形式排列的。
形式排列的,即按照t-行形式排列的。
文中需记录大量两站点i,j在Lk线路上所经过的站点数,它是三维数组,记公交地铁网络信息矩阵W=[wi,jk]n×n×m,wi,jk表示i,j两站点在Lk线路上所经过的站点数,m表示有m条公交地铁线路,n表示有n个公交地铁站点。
2 公交地铁网络优化模型 2.1 公交地铁网络图公交地铁网络是由公交线路和地铁线路组成的网络[13],每条线路经过若干站点,每个站点有多条线路通过,记站点集合S={S1,S2,…,Sn},其中S1,S2,…,Sn为站点;线路集合L={L1,L2,…,Lm},其中L1,L2,…,Lm为线路。由站点集合S和线路集合L构成的二元组H={S,L}反映到图上,即为公交地铁网络图。
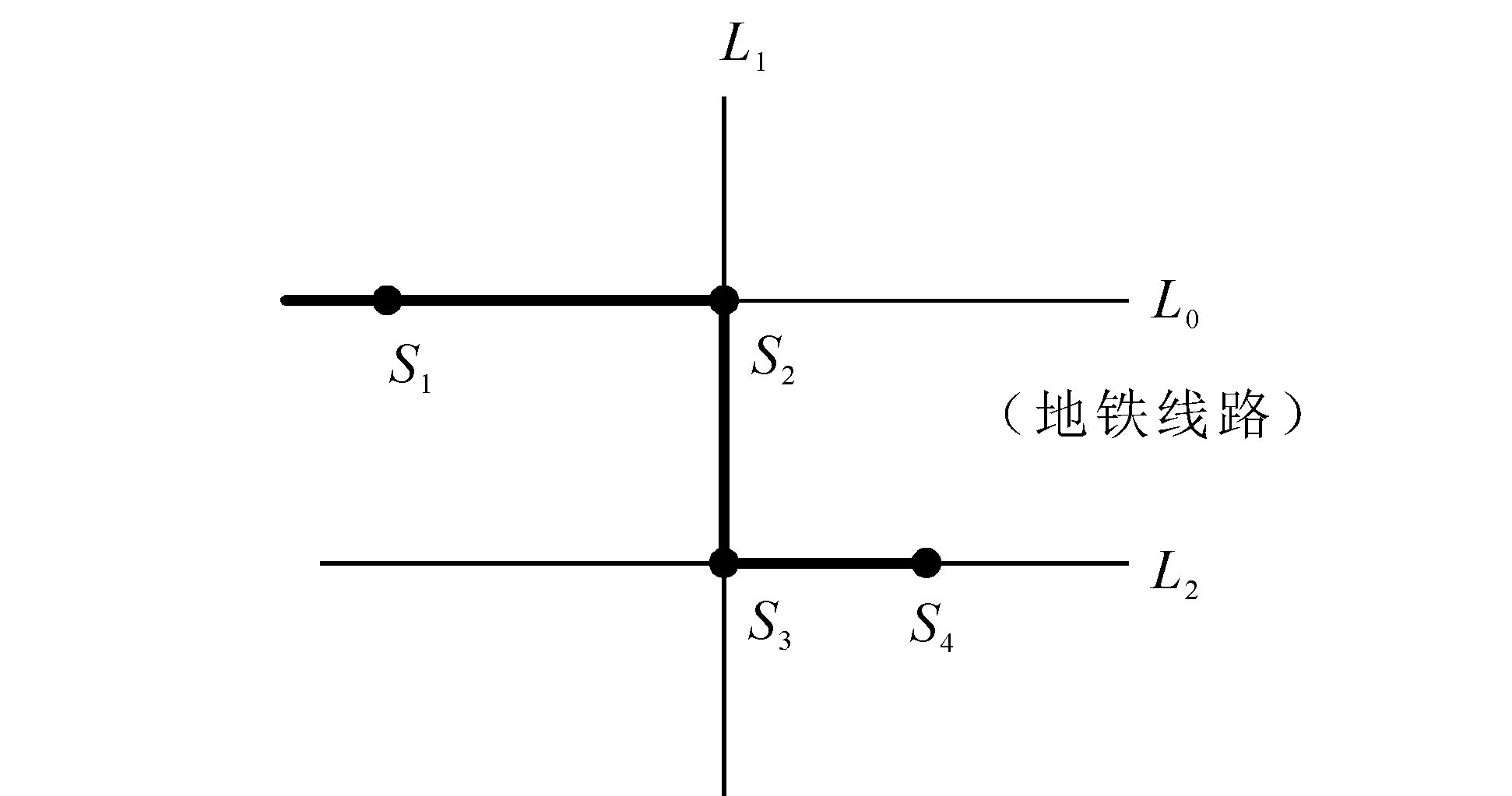
例如,某公交地铁网络由1条地铁线路、2条公交线路、2个地铁站点(地铁站点都为公交站点)和2个公交站点(不包含前述地铁站点)组成,他们分别为地铁线路L0,公交线路L1、L2,地铁站点S1、S2,公交站点S3、S4,如图 1。
|
| 图 1 公交地铁网络 Fig. 1 Bus and subway network |
公交地铁网络二分图是三元组G=(S,L,E),其中S和L是2个不相交的顶点集,分别为顶部和底部的顶点集,并且E⊆S×L是一个边集,边连接顶部和底部的顶点。
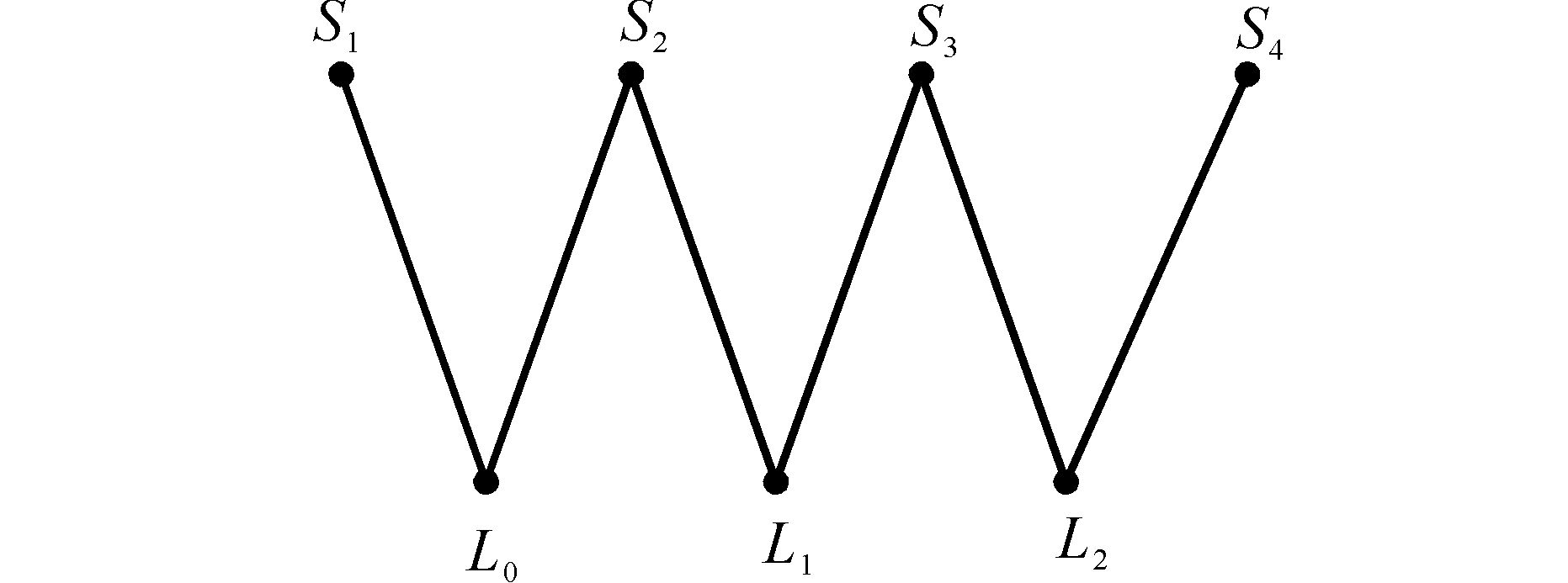
具有2种属性的复杂网络可用二分图表示[14, 15].公交地铁网络的站点和线路2种属性决定了它可以反映到二分图上。将顶点集合S看作二分图的上顶点集,线路集合L看作二分图的下顶点集,公交线路L′经过站点S′,则在L′线路与S′站点之间有边相连。图 2是图 1的公交网络对应的网络二分图。
|
| 图 2 网络二分图 Fig. 2 Bipartite network graph |
由图 2看出,S1与S2可直接到达,S1与S3需经过S2转乘,S1与S4需经过S2,S3转乘到达。二分图比网络图更加直观地显示出换乘次数。
2.3 公交地铁网络图的映射图公交地铁网络图的映射图包括线路映射网络图和站点映射网络图,可以由二分图得到。
二分图G=(S,L,E)的上顶点映射图(即站点映射网络图)为GS=(S,ES),边集ES= {SiSj|N(Si)∩N(Sj)≠∅},其中N(Si)为Si在二分图中的邻接点集合。它的下顶点映射图(即线路映射网络图)为GL=(L,EL),边集EL={LiLj|N(Li)∩N(Lj)≠∅},其中N(Li)为Li在二分图中的邻接点集合。线路映射网络图能反映出线路之间的连通关系,两站点所在的线路在线路映射网络图中所连接的边数反映了乘客的换乘次数。站点映射网络图表示站点之间的连通关系,它能反映出乘客换乘次数的同时,也给出了换乘站点。
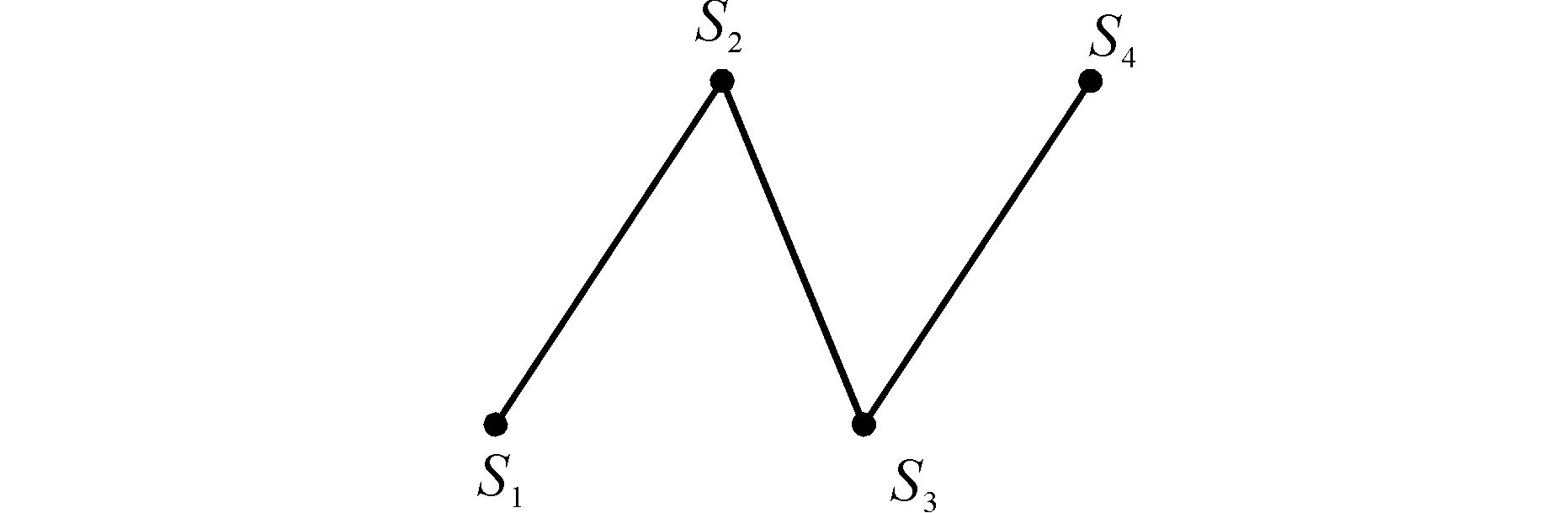
图 3为图 2的线路映射网络图,图 4为图 2的站点映射网络图。由图 3可以看出,L1与L0、L2之间分别为一条边,即若出发站点在L1站点上,目的地站点在L0站点或L2站点上,转乘1次公交或者地铁即可到达。若出发站点在L0线路上,目的地站点在L2线路上,则需在L1线路上的某2个站点处转乘,乘坐3次公交或地铁即可到达目的地。由图 4可以看出,S1与S2有一条边相连,即两站点在一条线路上,可以直达。S1与S3之间有2条边,且经过S2站点,则从S1站点到达S3站点必须在S2站点转乘,即坐2次公交或地铁到达。S1与S4之间有3条边相连,从图可直接看出,由S1站点出发,需在S2和S3站点转乘,以到达S4站点。

|
| 图 3 线路映射网络图 Fig. 3 Line mapping network graph |
|
| 图 4 站点映射网络图 Fig. 4 Site mapping network graph |
首先对每条线路上的站点进行一体化标号,考虑到地铁的快捷性、准时性、舒适性等优点,优选地铁出行是大势所趋。这样,将地铁线路上两站点间乘车距离权值适当减小,这样就达到了优选地铁出行的目的。
3.1 标号公交地铁网络的模型若线路Lk上有kn个站点,Lk:Sk1,Sk2,…,Skn,站点Skj在线路Lk上的标号为j,记为Njk=j,在二分网络图中边LkSkj的权值为该站点在线路Lk上的标号:Njk=j。
然后建立公交地铁线路映射网络和站点映射网络。在站点映射网络中,对边SiSj赋值,记为wi,jk,且wi,jk=|Njk-Nik|,它代表在Lk线路上Si、Sj两站点之间的站点数。若Si、Sj不在Lk线路上,令wi,jk=0。
3.2 基于标号网络模型最优路选择的算法
1)给出任两站点Si与Sj,构造直达检验向量αij=W▷ei▷ej,其中W=[wi,jk]n×n×m,ei表示第i个元素为1,其余全为0的n维单位向量,若αij=(wi,j1,wi,j2,…,wi,jm)|T≠0,则Si站点与Sj站点可以直达,若v=arg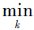 {wi,jk},则wi,jv为Si与Sj站点之间的最小直达距离,最优路径为Lv。
{wi,jk},则wi,jv为Si与Sj站点之间的最小直达距离,最优路径为Lv。
2)若Si站点与Sj站点不可直达,根据站点映射网络图,记与Si站点邻接的站点集合S′i={Si1,Si2,…,Sik}与Sj站点邻接的站点集合S′j={Sj1,Sj2,…,Sjl},若S′i∩S′j≠∅,则表示Si站点与Sj站点转乘一次可到达,记S′i∩S′j={Sr1,Sr2,…,Srp},则Si与Sj可经p种方法到达,则d(Si,Sj)=min{wi,rl+wr,jl′},Ll∈L,Ll′∈L′,根据公交网络二分图,L与L′分别为连接Si与Sr,Sr与Sj站点的线路,其对应的路线为最优出行路线。
3)若S′i∩S′j=∅,即一次转乘不可达,则检验S′i与S′j中有无可直达的两站点,若N(Sip)∩N(Sjq)≠∅,Sip∈S′i,Sjq∈S′j,则站点Sip与站点Sjq之间有直达线路,d(Si,Sj)=min{wi,ipl1+wip,jql2+wjq,jl3},Ll1∈L1,Ll2∈L2,Ll3∈L3,其中L1、L2、L3根据公交地铁网络二分图确定,且L1、L2、L3分别为连接Si与Sip,Sip与Sjq,Sjq与Sj站点的线路,其对应方案为最优出行方案。
调查表明,在一个成熟的公交地铁网络中,2次换乘可以实现绝大多数出发地与目的地之间的连接。
3.3 算法的复杂性分析算法的复杂性用数据输入规模的函数度量。由站点集合S={S1,S2,…,Sn}和公交线路集合L={L1,L2,…,Lm}组成的地铁公交网络,存储数据W=[wi,jk]n×n×m的规模为n2m。但因为W为稀疏三维数组,占用存储空间大大减小。在能够直达的情况下,算法的计算量主要为检验向量的计算上,运算量为O(n2m)。在不能直达情况下的转乘问题的计算量主要为寻找转乘站点和转乘线路的计算上。寻找转乘站点实质是在站点映射网络上寻找从Si到Sj的中间站点,可以在站点映射网络上采用经典最短路算法,如Dijkstra算法,运算量为O(n2)。在映射网络图上的求Si与Sj的最短路的最小优化问题,实质是多阶段决策问题,可以用经典动态规划或最短路算法来求解,计算量为O(m2)。总体上,该算法总的计算量为O(n2m)。
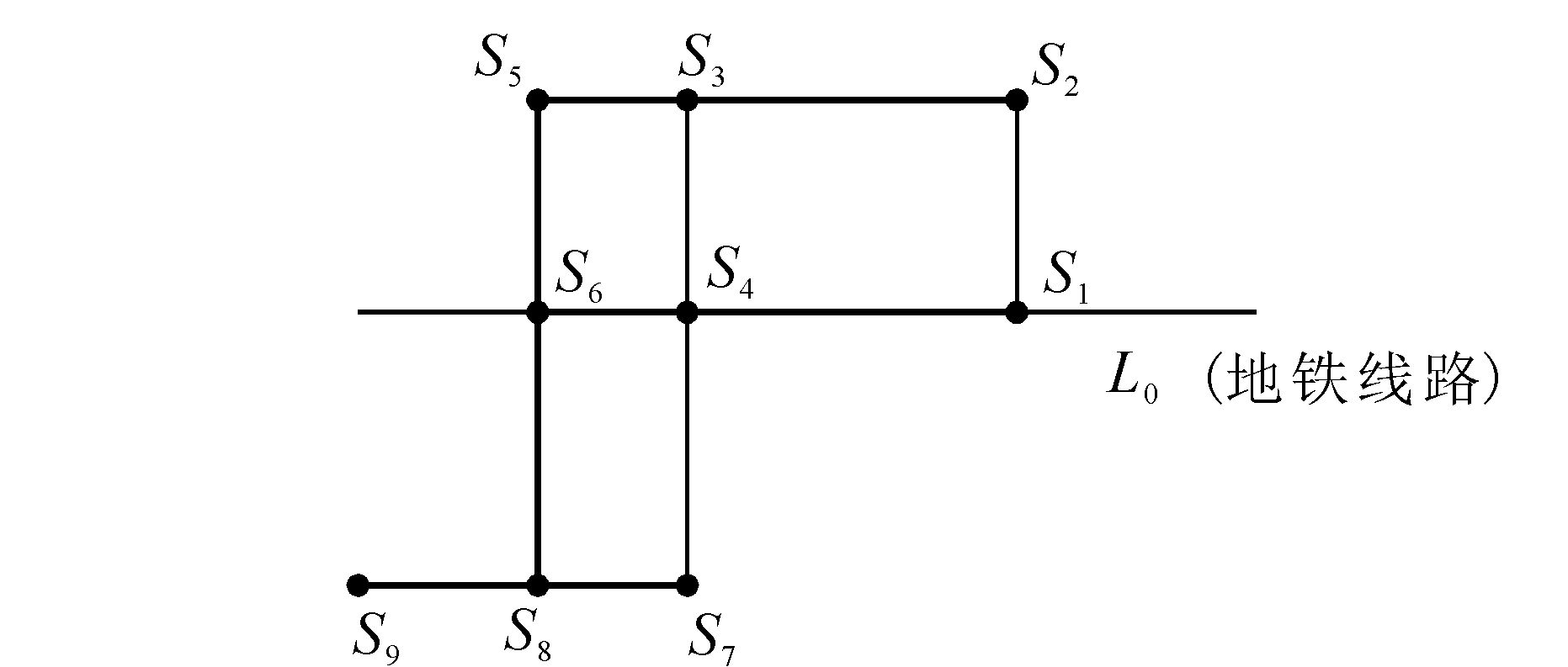
4 算 例选取由4条公交线路L1、L2、L3、L4,1条地铁线路L0及9个站点组成的公交网络,如图 5,地铁线路L0经S1、S4、S6站点,线路L1经S1、S2、S3站点,线路L2经S5、S3、S4、S7站点,线路L3经S5、S6、S8站点,线路L4经S8、S9站点。其中N10=1,N40=7,N60=10;N11=2,N21=5,N31=11;N52=6,N32=9,N42=12,N72=16;N53=6,N63=9,N83=13;N84=4,N94=9。
|
| 图 5 公交地铁网络 Fig. 5 Bus and subway network graph |
如第3节中对标号的叙述,为达到优选地铁的目的,不妨将地铁线路上站点的标号根据实际情况缩小适当倍,这样可将整个公交网络系统一体化处理。而实际上的目的是使地铁线路上的乘车距离权值变小,即需将标号之间的差值成比例缩小。此例中N10=1,N40=7,N60=10,按照式wi,jk=|Njk-Nik|,得w1,40=6,w1,60=9,w4,60=3。若将此权值3倍缩小可得出w1,40=2,w1,60=3,w4,60=1,其余公交线路上权值为w1,21=3,w1,31=9,w2,31=6;w3,42=3,w3,52=3,w3,72=7,w4,52=6,w4,72=4,w5,72=10;w5,63=3,w5,83=7,w6,83=4;w8,94=5。其余wi,jk赋值为零。
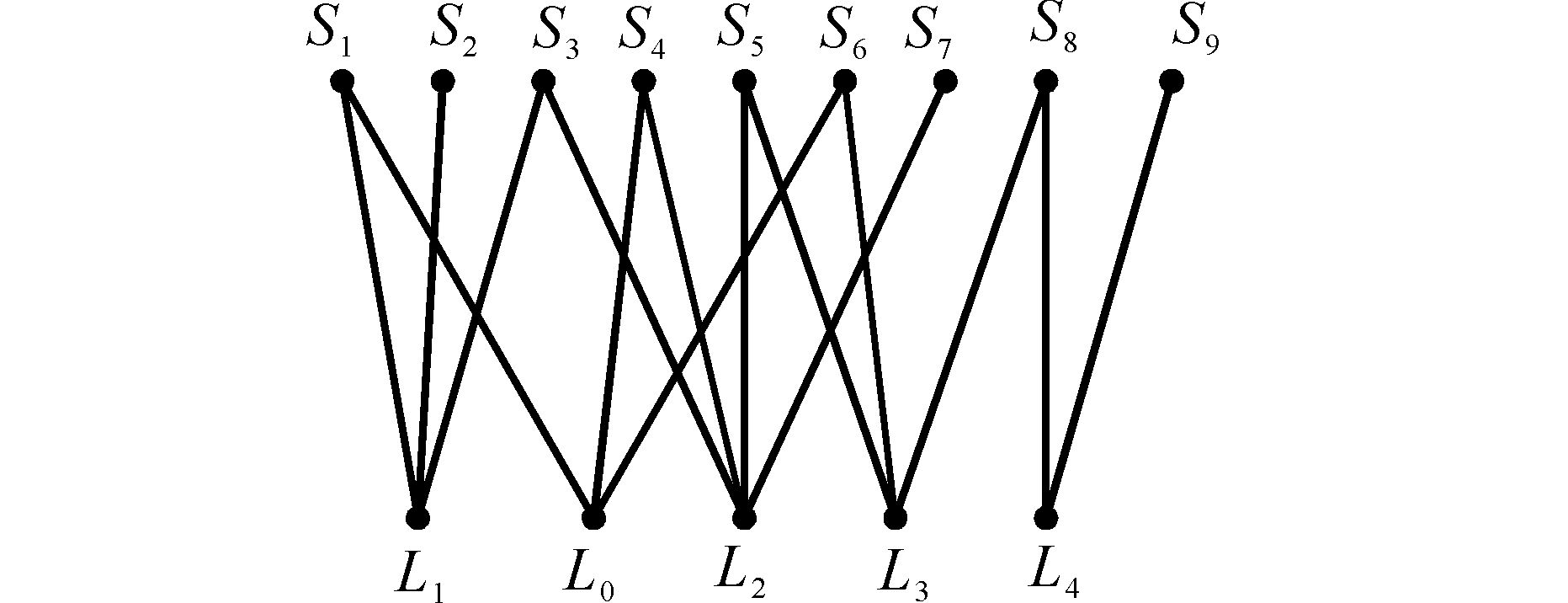
建立图 5的公交地铁网络二分图,如图 6。图 7为图 6的线路映射网络图,图 8为图 6的站点映射网络图。
|
| 图 6 网络二分图 Fig. 6 Bipartite network |

|
| 图 7 线路映射网络图 Fig. 7 Line mapping network |

|
| 图 8 站点映射网络图 Fig. 8 Site mapping network graph |
1)考虑站点S2到站点S3的最短路问题,构造直达检验向量α23=W▷e2▷e3,可得到α23=(w2,30,w2,31,w2,32,w2,33,w2,34)T≠0,若v=arg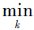 {w2,3k}=1,即w2,31=6为最小直达距离,L1为所选乘车路线,途径6站。
{w2,3k}=1,即w2,31=6为最小直达距离,L1为所选乘车路线,途径6站。
2)考虑站点S1到站点S5的最短路问题,α15=W▷e1▷e5=0,即不可直达,根据站点网络映射图,如图 8,得到与S1站点邻接的站点集合S′1={S2,S3,S4,S6},与S5站点邻接的站点集合S′5={S3,S4,S6,S7,S8},由于S′1∩S′5≠∅,表示S1站点与S5站点转乘1次可到达。又S′1∩S′5={S3,S4,S6},则S1站点与S5站点可经3种1次转乘的方案到达,d(S1,S5)=min{w1,31+w3,52,w1,40+w4,52,w1,60+w6,53}=min{9+3,2+6,3+3}=6,对应最优路径为从S1站点乘坐地铁线路L0到达S6站点,转乘公交线路L3到达S5站点,途经6站。
可看出,从S1站点到S5站点与从S2站点到S3站点都是经过6站地,而网络图中明显看出S1,S5站点的距离是远远大于S2,S3站点的距离,这是减少地铁站点标号的权值的结果。结果显示出地铁的优越性。
3)考虑站点S4到站点S9的最短路问题,S4在线路L0与线路L2上,S9在线路L4上,α49=W▷e4▷e9=0,即不可直达,S′4={S1,S3,S5,S6,S7},S′9={S8},S′4∩S′9=∅,即1次转乘不可达。下面考虑2次转乘的情况,根据线路网络映射图,L0或L2线路与L4线路之间有L3连接,即从L0线路或L2线路需转乘L3到线路上,再转乘到L4线路上。
根据网络二分图,可得:N(S1)={L1,L0},N(S3)={L1,L2},N(S5)={L2,L3},N(S6)={L0,L3},N(S7)={L2},而N(S8)={L3,L4},则N(S5)∩N(S8)≠∅,N(S6)∩N(S8)≠∅,即S′4中的S5站点与S6站点可与S8站点直达,而且它们分别都在L3线路上,则可求得
在文献[10]的基础上,将公交地铁进行一体化标号,缩小地铁两站点间的路径距离以达到优选地铁的目的。据乘客出行心理,依次以换乘次数少、出行距离短为优化目标,利用高维数组运算,根据公交地铁网络图与二分图、线路映射网络图、站点映射网络图得到两站点间的最优路径的选择算法。
公交网络的寻径问题一直以来被认为是NP难问题,而日益发达的公交系统对最优路径选择算法的要求也越来越高。因此,改进和创新算法在整个公交系统中至关重要。本文尚未将地铁的时变性考虑在内,可对此进一步研究,使得人们无论何时出行都有一个对应此时间点的方案,使查询更加精确可靠。
| [1] | 闫小勇, 尚艳亮. 基于二部图模型的公交网络路径搜索算法[J]. 计算机工程与应用, 2010, 46(5): 246-248.YAN Xiaoyong, SHANG Yanliang. Path-finding algorithm of public transport networks based on bipartite graph model[J]. Computer Engineering and Applications, 2010, 46(5): 246-248. |
| [2] | 梁虹, 袁小群, 刘蕊. 一种新的公交数据模型与公交查询系统实现[J]. 计算机工程与应用, 2007, 43(3): 234-238. LIANG Hong, YUAN Xiaoqun, LIU Rui. Novel model and realization of public transport route inquiring system[J]. Computer Engineering and Applications, 2007, 43(3): 234-238. |
| [3] | 王海帅, 冀振燕, 王森. 公交线路查询算法[J]. 计算机系统应用, 2013, 22(2): 88-91. WANG Haishuai, JI Zhenyan, WANG Sen. Bus transport transfer algorithm[J]. Computer Systems and Applications, 2013, 22(2): 88-91. |
| [4] | 王昉旸, 于丽娜, 郑保华, 等. “集合燃烧”算法在公交网络查询中的应用[J]. 辽宁工程技术大学学报: 社会科学版, 2008, 10(4): 380-382.WANG Fangyang, YU Lina, ZHENG Baohua, et al. “Aggregate-combustion” arithmetic and its application in the query system of transit network[J]. Journal of Liaoning Technical University: Social Science Edition, 2008, 10(4): 380-382. |
| [5] | 伍雁鹏, 彭小奇, 杨恒伏. 改进的基于关系数据库技术的公交查询算法[J]. 中南大学学报: 自然科学版, 2009, 40(3): 763-766.WU Yanpeng, PENG Xiaoqi, YANG Hengfu. Improved algorithm based on relational database technology for querying transit network[J]. Journal of Central South University: Science and Technology, 2009, 40(3): 763-766. |
| [6] | 刘健, 徐维祥, 刘旭敏. 公交出行最优路线查询系统设计[J]. 计算机应用, 2009, 29(S2): 110-112. LIU Jian, XU Weixiang, LIU Xumin. Design of urban public transit optimal route inquiry system[J]. Journal of Computer Applications, 2009, 29(S2): 110-112. |
| [7] | 伍雁鹏, 彭小奇, 黄同成. 基于路径集合运算的公交网络寻径算法研究[J]. 计算机科学, 2009, 36(6): 239-240, 272.WU Yanpeng, PENG Xiaoqi, HUANG Tongcheng. Research on path set operation based algorithm for path searching in public transit network[J]. Computer Science, 2009, 36(6): 239-240, 272. |
| [8] | 刘作虎, 黄明和, 邹小云, 等. 一种网络公交查询系统的改进算法[J]. 计算机与信息技术, 2009, (4): 29-31. |
| [9] | 徐勇, 李杰, 张军芳, 等. 新型公交网络模型与最优线路选择算法[J]. 系统工程理论与实践, 2011, 31(11): 2234-2240. XU Yong, LI Jie, ZHANG Junfang, et al. New urban transit network models and optimal path searching algorithm[J]. Systems Engineering—Theory and Practice, 2011, 31(11): 2234-2240. |
| [10] | 刘旭浩, 徐勇. 基于半张量积理论的公交网络查询[J]. 复杂系统与复杂性科学, 2013, 10(1): 38-44. LIU Xuhao, XU Yong. An inquiry method of transit network based on semi-tensor product[J]. Complex Systems and Complexity Science, 2013, 10(1): 38-44. |
| [11] | 张林峰, 范炳全, 吕智林. 公交网络换乘矩阵的分析与算法[J]. 系统工程, 2003, 21(6): 92-96. ZHANG Linfeng, FAN Bingquan, LV Zhilin. Transfer matrix of public transit network and algorithm[J]. Systems Engineering, 2003, 21(6): 92-96. |
| [12] | 程代展, 齐洪胜. 矩阵的半张量积理论与应用[M]. 北京: 科学出版社, 2007. |
| [13] | YAO Baozhen, HU Ping, LU Xiaohong, et al. Transit network design based on travel time reliability[J]. Transportation Research, Part C: Emerging Technologies, 2014, 43(3): 233-248. |
| [14] | 张译, 靳雪翔, 张毅, 等. 基于二分图的城市公交网络拓扑性质研究[J]. 系统工程理论与实践, 2007, 27(7): 149-155. ZHANG Yi, JIN Xuexiang, ZHANG Yi, et al. Topological analysis of urban transit networks using bipartite graph model[J]. Systems Engineering—Theory & Practice, 2007, 27(7): 149-155. |
| [15] | 王炜, 杨新苗, 陈学武. 城市公共交通系统规划方法与管理技术[M]. 北京: 科学出版社, 2002. |



