随着人们对电子商务交易智能化、个性化需求的提高,实现电子商务谈判的智能化和个性化已经成为下一代电子商务的发展方向。目前,电子商务自动谈判的研究已成为多主体系统的典型应用之一[1]。相对于传统的谈判支持系统,自动谈判可以在一定程度上代替人进行谈判,能够优化谈判过程,提高谈判效率,节约成本。尤其是实现异地远程商务谈判的自动化与决策支持,具有重要的研究价值。
从20世纪90年代初,国内外学者开始研究电子商务自动谈判模型,陆续研发出一些有实际应用价值的自动谈判系统,例如有慎思机制的谈判模型、在线拍卖网站AnctionBot系统、具有学习能力的谈判系统等。随着Agent的引入,电子商务谈判系统开始有了新的发展方向。而多个Agent的自动谈判技术弥补了传统谈判信息不对称的不足,更符合电子商务谈判对速度快、整体效益需求高的要求。现有关多Agent谈判模型和算法的研究较少,并且存在一些不足。诸如:1)现有自动谈判模型大都采用一旦发现Agent相匹配即退出的模式,Agent匹配到的不一定是使整体效用最大的Agent;2)使用较为成熟的智能算法,如模拟退火算法[1]、遗传算法[2]、贝叶斯学习或建立效用函数等,而一些新兴算法如蝙蝠算法、人工鱼群算法、人工蜂群算法等尚未用到,这些新兴算法在解决实际问题中有其自身优势;3)基于传统经典理论的谈判算法具有很强的针对性,应用在不确定性很大的网络环境中有一定困难。针对上述现有电子商务自动谈判模型的局限性,本文引入了新的模型和求解算法来解决上述问题。
2005年,Karaboga提出了一种基于蜜蜂群体觅食行为的群智能优化算法—人工蜂群算法(artificial bee colony algorithm,ABC)。该算法参数较少,全局收敛性也较好,适用于多维问题的求解。ABC算法模拟蜂群的集体行为,蜜蜂群依据各自分工不同进行不同活动,通过交换信息来寻找最佳蜜源。蜂群算法的算法流程与多Agent系统的自动谈判模型有一定的相似性,如蜜蜂寻找含蜜量多的蜜源,相当于Agent寻找与之匹配的Agent;蜜蜂多次探索寻找全局最优解,相当于Agent匹配到使整体效用最大的Agent。而且基于蜂群算法的算法流程与多Agent系统的自动谈判模型之间的相似性,可以对人工蜂群算法进行改进,并添加学习机制,使之更适用于电子商务环境下多Agent自动谈判模型的求解。
1 电子商务自动谈判 1.1 特征选取和内容相似度计算多Agent系统(multi-Agent system,MAS)中,每一个Agent是独立和自治的,不仅要有自主性、反应性、能动性、时间连续性及其个性偏好,还要能够和其他Agent进行交互[4]。在谈判过程中,各个Agent相互之间通过竞争、协商、合作等手段达到利益最大化的目的。多Agent系统结构有集中式和分布式2种,本文研究分布式结构的多Agent系统。在分布式结构中,Agent之间是平等合作的关系。自动谈判模型中的Agent还应该具有如下3个特性:
1)择优选择。Agent每一次的选择使得自身效用函数最大,所有Agent在动态变化的环境中选择的结果使得整个系统的利益达到最大。
2)自我学习。单个Agent有自己的历史经验库、数据存储、处理过程和处理机,在与整个系统交互的过程中,Agent根据外界环境变化的信息,经过分析处理反馈出对自己有利的当前状态,同时更新历史经验库和数据存储。即Agent经过了自我学习的过程。
3)服从协议。为保证谈判过程的正常执行,Agent必须执行谈判协议规定的行动方案,使得谈判各方解决冲突,最终达成一致协议。
1.2 Agent属性的权重和效用每个Agent在谈判过程中有多个谈判属性,即谈判中考虑的问题,每一轮谈判中各个属性的效用值之和是这个Agent在此次谈判中所获得的效用。设每个Agent有M项属性,按照自己的偏好对各项属性分别设置权重WM。N个Agent的权重矩阵为


对每项属性的效用值设定上限和下限,在自动谈判过程中每项属性只能在此范围内进行调整,如式(1):
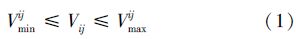
电子商务自动谈判过程主要分为6步:需求确定、商品代理(信息搜寻)、商家代理、谈判、支付与配送、商品服务与评价。第2步到第4步为谈判系统的核心,也是自动谈判系统研究的重点。经典的电子商务多对多谈判机制中交易双方都有多个,且供应方和需求方数量不一定相等,谈判的内容不止一项,与现实生活中的电子商务市场一致,本文这里研究多对多的多属性自动谈判问题。
首先,确定多对多自动谈判协议。发起谈判时,确定参与谈判各方。发送身份验证,确认谈判中用于保障数据安全的公钥和各自的私钥。谈判过程中,采用改进让步协议[6],如果当前Agent匹配到另外一个Agent的要求,那么就暂时达成一个协议。此时若没有合适当前Agent的匹配,则Agent让步或者进入下一轮谈判。Agent通过调整各项属性的效用值来实现让步,并且不能使所有属性值同时提高,降低一个属性的效用值,相应地提高另一个属性的效用值。例如,若实际谈判中需方Agent接受较远的产地,则相应地要求提升产品质量,其让步过程可描述为
如果在某一步中,没有Agent让步,那么谈判结束或者协议指出已经产生了一个死锁。在谈判中Agent不能放弃,也不能同时多轮都不变化。在自动谈判过程中,如果有Agent无法匹配到其他Agent要求,且经过多轮让步都无法匹配,则该Agent自动退出谈判,不影响谈判继续进行。此协议的优点是,它能够保证收敛或者当不能够收敛时,可以快速结束谈判。在此协议中,为满足这个规则,Agent必须相互知道对方的效用矩阵。
2 人工蜂群算法的谈判模型设计 2.1 人工蜂群算法基本原理在蜜蜂群体采蜜的过程中,传递蜜源的位置、含蜜量等信息,以便大量蜜蜂飞往优秀蜜源采蜜是最重要的部分。因此,人工蜂群算法首先将蜂群分为引领蜂(employed bees)、跟随蜂(onlookers)和侦察蜂(scouts)3类。出去寻找蜜源的蜜蜂是引领蜂,在舞蹈区内等待选择蜜源的蜜蜂是跟随蜂,而在一定情况下进行随机搜索蜜源的蜜蜂是侦察蜂。蜂群数量的一半是引领蜂,另一半是跟随蜂,引领蜂的数量和食物源的数量相等。
在蜂群进化过程中,引领蜂和跟随蜂负责执行开采过程,而侦察蜂执行探索过程。蜜蜂执行搜索活动的主要过程如下:
1)随机初始化引领蜂的位置,发现初始蜜源并记忆当前蜜源位置,根据记忆的局部信息,在领域范围内搜索新蜜源。根据蜜源的花蜜数量选择最优位置。
2)引领蜂通过跳摇摆舞将蜜源信息分享给跟随蜂,跟随蜂通过轮盘赌来选择一个蜜源。再在此蜜源附近利用其记忆中的局部信息选择一个新蜜源,比较新位置和原位置的花蜜数量,若新位置的花蜜量高于原位置,则记住新位置。
3)一个食物源经过Nlimit代(Nlimit为自定义常量),其适应度都没有任何改变,则当前食物源被放弃,且当前食物源处的引领蜂变为侦察蜂,并开始随机搜索新的蜜源。
4)记录迄今为止最好蜜源,作为全局最优解输出。
人工蜂群算法反馈机制优越,食物源的花蜜量与食物源被选择的可能性成正比,蜜蜂能及时停止对较差食物源的开采。且蜜蜂能与其他蜜蜂共同分享食物源的信息。这对自动谈判过程中,供应商的选择、属性调整以及快速寻找匹配Agent的过程具有有益的参考价值。
2.2 人工蜂群算法建模及求解结合人工蜂群算法原理和Agent自动谈判过程,可以假设供应方为食物源,需求方为蜜蜂,每一个供方和需方为一个Agent,食物源的花蜜量由Agent的效用值来决定。设供方有N个,需方有X个。与电子商务市场实际情况相结合,供应方和需求方数量不一定相等,谈判结果也不一定是供方和需方一一对应,因此将N个供方模拟为rN(r=1,2,…,n)个食物源,即每个供方Agent有r次被选择的机会,此处r取决于实际问题的计算规模,r取值越大,计算结果趋向于整体效用值更优,但是计算时间也越长。
设每个Agent有M项属性,各项属性的权重为Wi(Wi∈(0,1))。第j个Agent的第i项效用值为Vij(Vij∈{0,1,2,…100}),效用值的上限和下限分别为Vijmin和Vijmax。则谈判过程中总体效用值如式(2)所示。求最大总体效用即为求模型的目标函数ftotal的最大值,目标函数ftotal如式(3)所示。
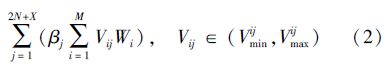

计算中,如果需方Agent的属性值高于当前匹配的供方Agent属性值,则需方Agent的效用系数βj=0,反之βj=1。若需方Agent的M项属性中有M1项属性值低于供方Agent属性,则βj值用式(4)求解。
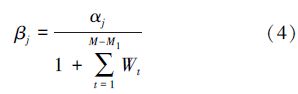
设引领蜂数量与需求方数量相等为X,跟随蜂数量也为X。首先,对供方Agent和需方Agent进行一次随机匹配,将匹配结果作为引领蜂的初始位置。其次,求出当前的目标函数值ftotal。然后,利用式(5)对Agent的属性值进行调整,权重越大的属性值被调整的概率越小,计算调整后的目标函数值与调整前相比取最优。
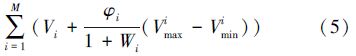
在引领蜂选择的基础上,X个跟随蜂利用式(6)在rN个位置中选择蜜源。跟随蜂选定所在位置后,利用式(7)进行属性调整,选择调整后的最优位置为跟随蜂的位置,并记录当前最好解。
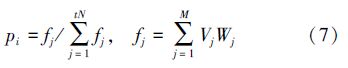
遍历所有蜜源,当一个蜜源效用值在Nlimit代内没有变化,当前位置的跟随蜂变为侦查蜂。寻找从未被选择过的蜜源x,利用式(8)进行试探性匹配,若f1>0则当前位置被蜜源x替换;如果所有蜜源都被选择过,则随机挑选一个蜜源k利用式(9)进行试探性交换匹配,若f2>0则当前位置被蜜源k替换。

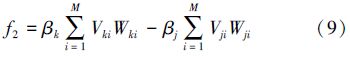
最后,计算当前目标函数ftotal值是否达到要求,达到要求则输出结果,否则算法继续。
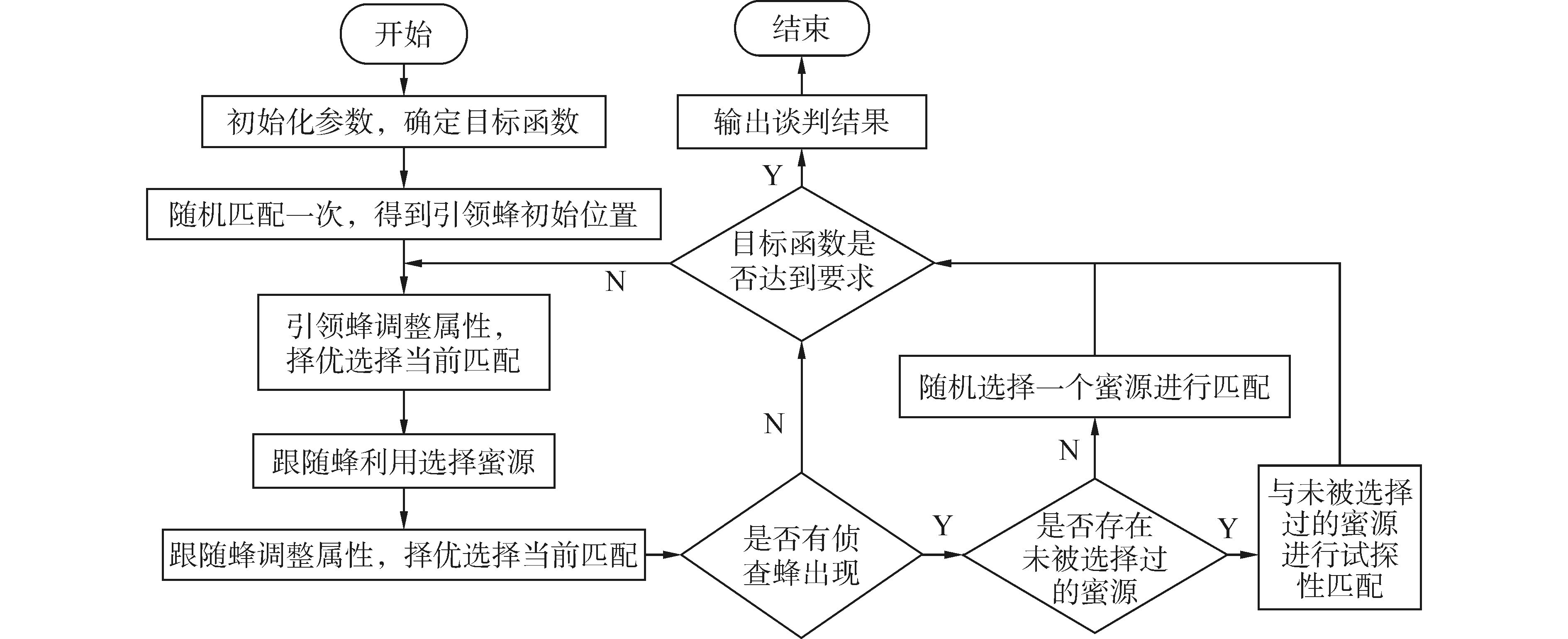
图 1为整个自动谈判模型的建模计算过程。
|
| 图 1 建模计算流程 Fig. 1 The modeling flow chart |
企业A、B、C分别需要采购一种工业原材料,3家企业对原材料的运输(Delivery)、质量(Quality)、价格(Price)分别有各自的要求。3家采购企业属性效用值如表 1所示,当前有4家供应商可供选择,分别为Q、W、E、R,每家供应商产品和服务都各有特色,4家供应商的属性如表 2所示。
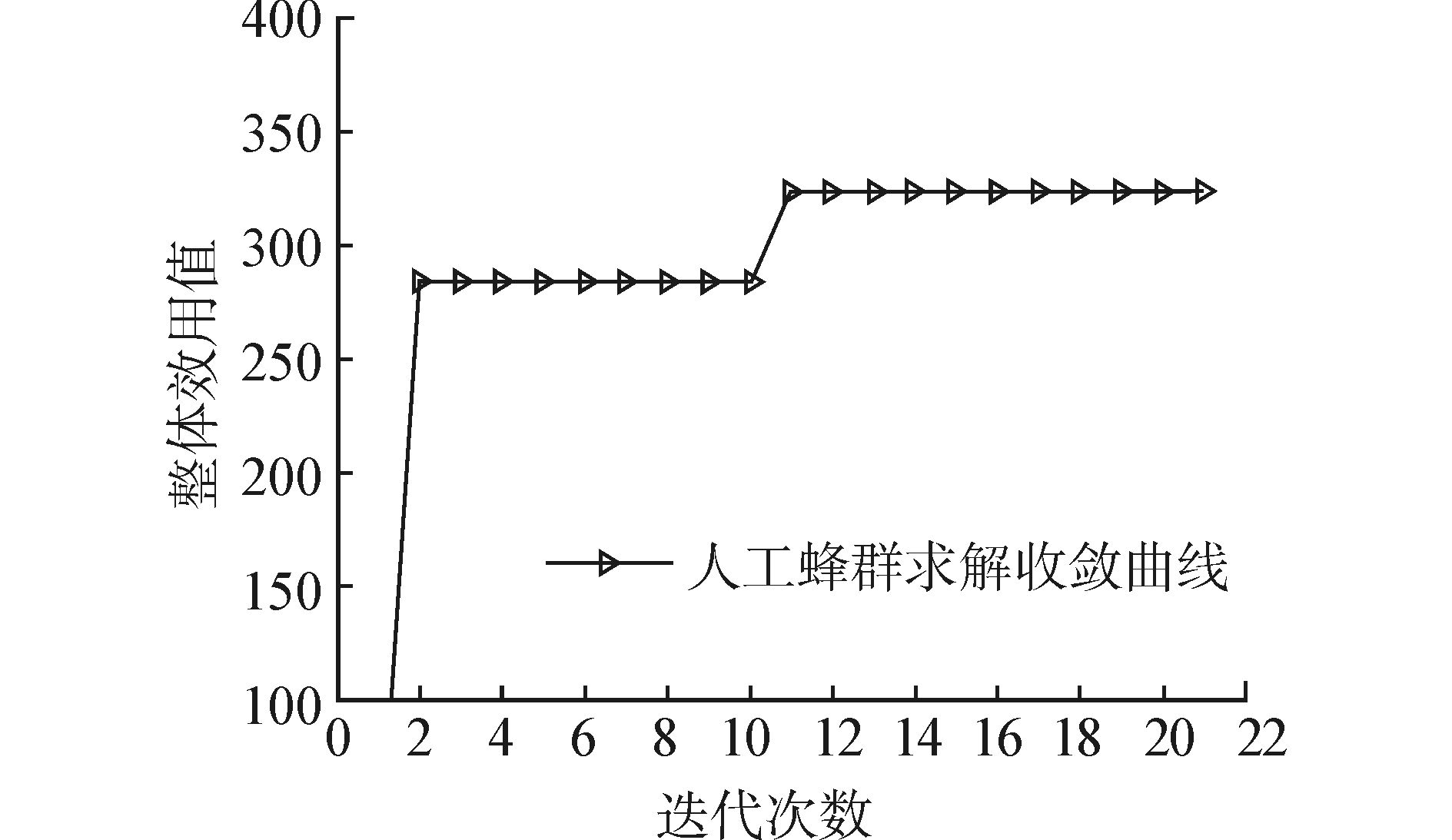
应用本文建模方法,首先从表 1和2得到权重矩阵W、效用值矩阵V和效用调整范围{Vmin,Vmax}。主要参数设置为属性最大范围参数P=10,蜜源数量2N=8,引领蜂数量X=3,属性数M=3,r=2。图 2为人工蜂群算法模型求解的计算收敛曲线,从图中可看出,算法循环20次后最好解不再变化,平均每次运行用时1.843 0 s,整体效用值最大为322.922(保留小数3位)。此时,需求企业A选择供应商R,B选择Q,C选择W。当前所有Agent属性效用值如表 3所示。
| 企业 | 运输D | 质量Q | 价格P | ||||||
| 效用值 | 效用值可调整范围 | 权重 | 效用值 | 效用值可调整范围 | 权重 | 效用值 | 效用值可调整范围 | 权重 | |
| A | 5.5 | [4.9,10] | 0.15 | 6.5 | [5.8,10] | 0.28 | 7.0 | [6.2,9.0] | 0.57 |
| B | 8.2 | [7.5,10] | 0.47 | 7.0 | [6.4,10] | 0.32 | 5.2 | [4.6,9.0] | 0.21 |
| C | 6.2 | [5.5,10] | 0.10 | 8.7 | [8.0,10] | 0.61 | 5.6 | [5.1,9.0] | 0.29 |
| 企业 | 运输D | 质量Q | 价格P | ||||||
| 效用值 | 效用值可调整范围 | 权重 | 效用值 | 效用值可调整范围 | 权重 | 效用值 | 效用值可调整范围 | 权重 | |
| Q | 7.5 | [0,8.2] | 0.62 | 6.6 | [0,7.2] | 0.28 | 4.5 | [1,5.1] | 0.10 |
| W | 6.0 | [0,6.5] | 0.21 | 8.4 | [0,8.9] | 0.59 | 5.0 | [1,5.5] | 0.20 |
| E | 5.2 | [0,6.0] | 0.11 | 6.0 | [0,6.6] | 0.19 | 8.0 | [1,8.3] | 0.70 |
| R | 6.6 | [0,7.0] | 0.30 | 7.1 | [0,7.7] | 0.31 | 6.1 | [1,6.6] | 0.39 |
|
| 图 2 模型计算收敛曲线 Fig. 2 The convergence curve |
| 企业 | 运输D | 质量Q | 价格P |
| A | 5.5 | 6.5 | 6.5 |
| B | 7.8 | 6.7 | 4.8 |
| C | 6.0 | 8.5 | 5.2 |
| Q | 7.9 | 6.9 | 4.9 |
| W | 6.2 | 8.6 | 5.4 |
| E | 5.2 | 6.0 | 8.0 |
| R | 6.6 | 7.1 | 6.6 |
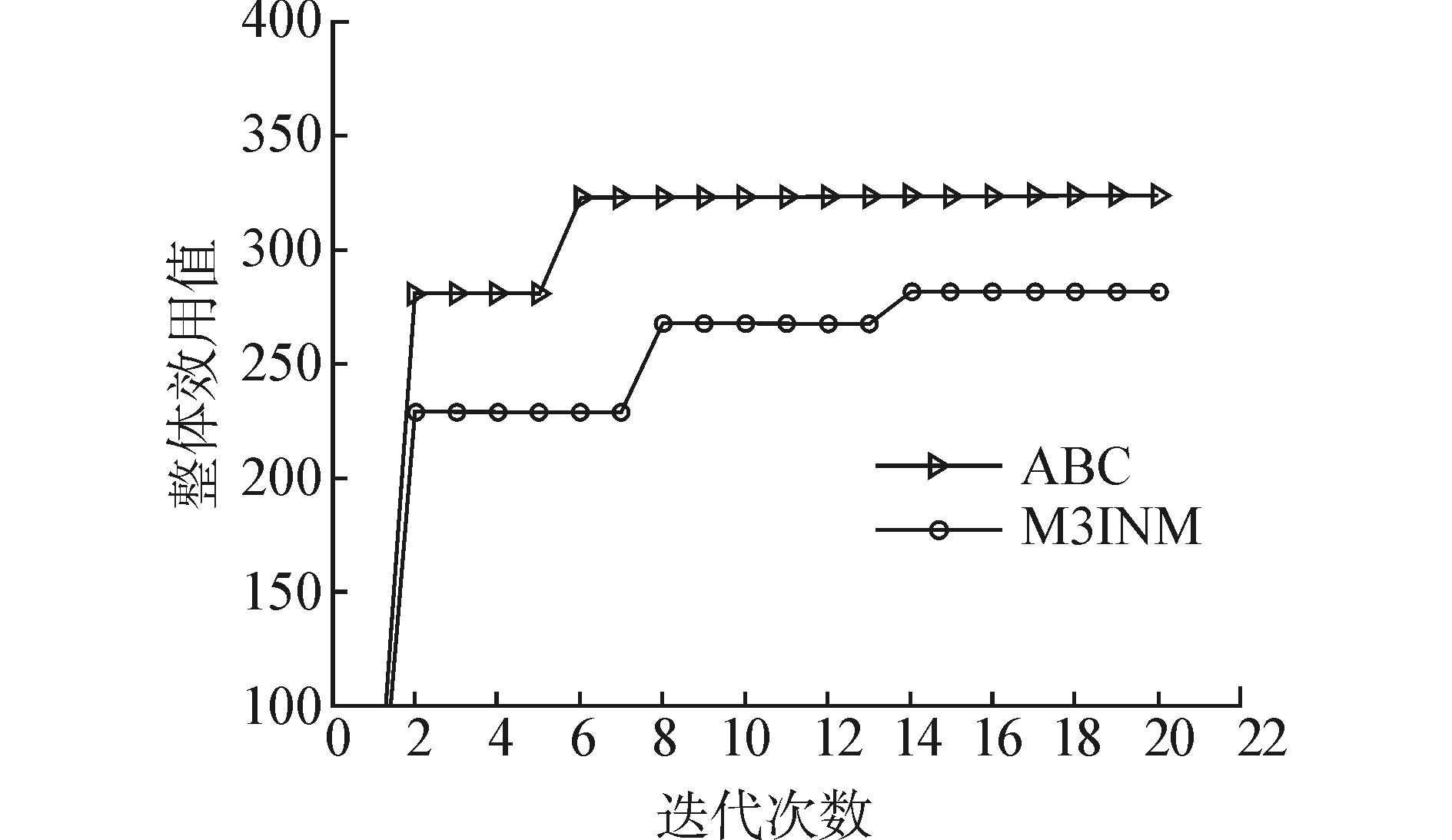
文献[1]给出的多Agent、多Object谈判方法(M3INM)中,当Object=1时,该模型描述的问题和本文类似。为验证本文模型的高效性,用文献[1]中的M3INM模型对本文算例进行求解,并与ABC算法的求解结果进行对比。本文模型迭代1次需要1.843 s,循环20次求得最好解为322.922;M3INM模型迭代1次需3.254 s,循环20次求得最好解为321.958。本文模型和M3INM模型分别运行50次,结果如表 4所示,从表中可看出本文算法计算结果及求解速度都优于文献[1]。图 3为ABC算法与M3INM模型求解结果的对比图,从图中可以看出,ABC算法求解性能优于M3INM,10代以内就能收敛到全局最优解,M3INM到第20代整体效用值都没有达到300。
| 方 法 | 迭代次数 | t代内平均值 | 最大值 | 时间/s |
| ABC算法 | 20 | 320.842 1 | 322.922 | 1.843 0 |
| M3INM模型 | 20 | 291.593 1 | 321.958 | 3.254 0 |
|
| 图 3 收敛性对比 Fig. 3 Convergence performance comparison |
本文将人工蜂群算法与多Agent多属性自动谈判模型相结合,设计了自动谈判模型及求解过程,提供了一种电子商务自动谈判问题的建模求解新思路,具有较强的适用性,能快速找到所有Agent总效用最大的谈判结果。实例测试结果及与其他模型的对比,验证了本文模型的有效性。国内外目前对大数据量自动谈判系统的研究较少,本文后续研究方向为建立基于人工蜂群算法的一般模型,用于解决大量Agent多属性谈判问题。
| [1] | FEI Yulian, CHEN Wenjuan. A multi-agent, multi-object and multi-attribute intelligent negotiation model[C]//Fourth International Conference on Fuzzy Systems and Knowledge Discovery. Haikou, China, 2007, 3: 440-446. |
| [2] | 黄京华, 马晖, 赵纯均. 面向电子商务的基本遗传算法的Agent谈判模型[J]. 管理科学学报, 2002, 5(6): 17-23.HUANG Jinghua, MA Jun, ZHAO Chunjun. Multi-agent negotiation model based on genetic algorithm in E-business[J]. Journal of Manegement Sciences in China, 2002, 5(6): 17-23. |
| [3] | ARGONETO P, RENNA P. Production planning, negotiation and coalition integration: A new tool for an innovative e-business model[J]. Robotics and Computer-Integrated Manufacturing, 2010, 26(1): 1-12. |
| [4] | CHHETRI M B, LIN J, GOH S K, et al. A coordinated architecture for the agent-based service level agreement negotiation of web service composition[C]//The Australian Software Engineering Conference. Sydney, Australia, 2006: 90-99. |
| [5] | HUANG C C, LIANG W Y, LAI Y H, et al. The agent-based negotiation process for B2C E-commerce[J]. Expert Systems with Applications, 2010, 37(1): 348-359. |
| [6] | 高珊, 张惠珍, 马良. 元胞人工蜂群算法及其在0-1规划问题中的应用[J]. 数学理论与应用, 2014, 34(1): 83-91.GAO Shan, ZHANG Huizhen, MA Liang. Cellular artificial bee colony algorithm and its application to 0-1 programming problems[J]. Mathematical Theory and Applications, 2014, 34(1): 83-91. |
| [7] | REN Z, ANUMBA C J, UGWU O O. The development of a multi-agent system for construction claims negotiation[J]. Advances in Engineering Software, 2003, 34(11/12): 683-696. |
| [8] | 孙华梅, 李一军, 曹荣增, 等. 基于约束放松的电子商务协同谈判模型[J]. 运筹与管理, 2008, 17(4): 132-137. SUN Huamei, LI Yijun, CAO Rongzeng, et al. Collaborative negotiation model based on relaxative constraints for E-commerce[J]. Operations Research and Management Science, 2008, 17(4): 132-137. |
| [9] | RAHWAN I, KOWALCZYK R, PHAM H H. Intelligent agents for automated one-to-many e-commerce negotiation[J]. Australian Computer Science Communications, 2002, 24(1): 197-204. |
| [10] | BADICA C, GANZHA M, PAPRZYCKI M. Developing a model agent-based e-commerce system[M]//LU Jie, ZHANG Guangquan, RUAN Da. E-service Intelligence. Berlin/Heidelberg: Springer, 2007: 555-578. |
| [11] | 王海, 李一军, 侯新培. 基于Agent的电子商务自动谈判系统研究[J]. 系统工程理论与实践, 2005, 25(11): 14-19. WANG Hai, LI Yijun, HOU Xinpei. E-commerce oriented ANS based on Agent[J]. Systems Engineering—Theory & Practice, 2005, 25(11): 14-19. |
| [12] | 高珊, 张惠珍, 马良. 蜂群算法求解支持模糊QoS约束的电子采购模型[J]. 经济数学, 2014, 31(2): 59-63. GAO Shan, ZHANG Huizhen, MA Liang. Solving E-procurement model based on fuzzy QoS-constraint with bee colony algorithm[J]. Journal of Quantitative Economics, 2014, 31(2): 59-63. |



