2.北方工业大学 城市道路交通智能控制技术北京市重点实验室, 北京 100144
2. Beijing Key Lab of Urban Intelligent Traffic Control Technology, North China University of Technology, Beijing 100144, China
大自然中的萤火虫种类多种多样,萤火虫通过身体发光来达到各种生存目的。一般说来,萤火虫的荧光素亮度越大越能找到其他萤火虫或越容易找到食物。最后,由于寻找同伴或者食物的原因导致许多萤火虫汇聚在一起。以此为启发,K. N. Krishnanad和D. Ghose总结形成了基本的人工萤火虫算法(glowworm swarm optimization,GSO),萤火虫最终会聚集成多个群体从而找到多个局部最优值,算法设计的迭代机制不仅有利于求解局部最优解,而且能够有助于快速求解全局最优值。所以,算法的优点是在搜索局部和全局最优解上具有速度快、效率高的特点,尤其在多模态函数求解问题等优化方面有着广泛的应用,如模拟机器人、多信号源追踪和定位、传感器的噪声测试等方面[1, 2, 3, 4]。但另一方面,该算法也存在着一些问题,如算法全局最优解的搜索受到约束,存在陷入局部最优的风险。由于算法设计的萤火虫移动步长是固定的,不利于算法后期求解局部最优值,而步长自适应调整有利于提高求解的精度和收敛速度。周正新[5]和欧阳喆等[6]通过自适应调整算法不同阶段的移动步长,算法初期采取较大的步长有助于快速找到全局最优邻域,而后期较小的步长有利于精确求解局部最优和加快收敛速度。
自适应步长提高了算法的性能,但是在寻优的精度和稳定性方面还存在不足。本文针对基本和自适应步长的算法在迭代过程中出现的萤火虫邻域集合为空集时,导致算法收敛速度降低并很快陷入局部最优的问题,提出了一种改进的自适应步长的人工萤火虫算法,即基于觅食行为的自适应步长人工萤火虫算法。
1 人工萤火虫算法原理 1.1 基本的人工萤火虫算法人工萤火虫算法(GSO)[7]是在2005年由K. N. Krishnanad和D. Ghose提出的一种新的群智能仿生优化算法。算法模拟了自然界中萤火虫求偶行为或者说是觅食行为。
GSO算法主要有4个阶段:萤火虫初始化阶段、荧光素更新阶段、位置移动阶段以及动态感知范围更新阶段。算法流程如图 1所示。
1)初始化阶段。
初始化算法各个参数、各萤火虫的位置。萤火虫随机分布在目标可行域中,每只萤火虫携带的初始荧光素l0和感知半径r0是相同的。
2)荧光素更新阶段。
萤火虫的荧光素大小与其所在搜索空间中的位置有直接关系,萤火虫所在空间位置的评价值越高,则荧光素更新后的增长就越大,即萤火虫的发光强度也越大。另外,萤火虫的发光强度的强弱除了受所在空间值的影响,还和萤火虫上一次迭代的荧光素大小以及挥发速度的快慢有关联,萤火虫位置更新完成后,下一次迭代开始前,所有萤火虫的荧光素都会更新,荧光素根据式(1)更新:
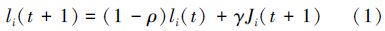
3)位置移动阶段。
算法每次迭代后萤火虫会在搜索空间中更新自己的位置,即位置移动。在萤火虫i位置移动之前必须先找到一个符合条件的同伴,这个同伴必须满足以下2个条件:a)要在萤火虫i的感知范围内;b)携带的荧光素值要大于萤火虫i的荧光素值。
在全部满足以上2个条件的萤火虫中,根据式(2)计算选择每个同伴萤火虫的概率大小:
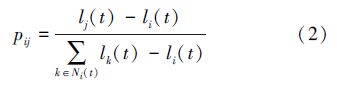
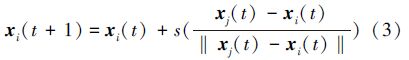
4)动态感知范围更新阶段。
萤火虫位置更新后,会动态调整自身感知范围,调整的大小是基于感知范围内同伴的数量多少。具体根据式(4)进行计算:
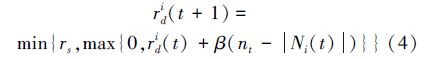

|
| 图 1 基本的GSO算法流程 Fig. 1 Flow chart of basic GSO algorithm |
2011年欧阳喆等[6]提出了一种自适应步长算法(adaptive-step GSO,A-GSO),引入荧光因子概念以在算法搜索过程中动态改变萤火虫移动步长,使算法避免陷入局部最优,提高寻优速度和精度。
荧光因子为
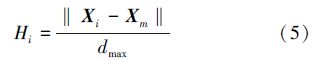
基于荧光因子的自适应移动步长按照式(6)进行调整。
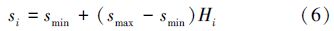
在GSO以及A-GSO算法中,算法运行过程中可能出现一些萤火虫的邻域萤火虫集合Ni(t)为空集的现象,对这些萤火虫的在算法迭代过程中将会出现位置不移动的情况,这将导致算法收敛速度降低并易陷入局部最优值。2011年张军丽等[8]提出了利用人工鱼群的觅食行为选择下一个移动的位置,但是没有考虑步长的自适应调整。本文借鉴觅食行为,设计了邻域集合为空集的萤火虫自适应步长移动策略,提出一种改进的基于觅食行为的自适应步长的人工萤火虫算法(foraging-behavior adaptive-step GSO,FA-GSO),算法改进的基本思想是在邻居集合Ni(t)为空集的萤火虫位置更新前,先在其动态决策范围Ni(t)内执行觅食行为,将该位置作为萤火虫在下一时刻移动的方向,计算荧光因子得出动态调整的移动步长(自适应步长),然后进行位置的移动,接着更新萤火虫的感知范围,最后计算萤火虫的荧光素。这样在不影响算法整体求解效率的基础上能够进一步精确、快速求解最优值。
具体改进如下,当Ni(t)为空集:萤火虫在其动态决策半径rdi(t)内执行觅食行为,设定觅食次数最大值为N次,该值的大小将影响算法迭代的精度和效率,如何设定合理的觅食次数使得算法在搜索精度和迭代效率2个方面得到较好的性能平衡,对于改进的算法有着重要的意义。具体在实现中,有多种设计方法,可以将该值设置为固定值,也可以在一定范围内进行随机设置。萤火虫每次觅食意味着寻找下次迭代移动方向,如果存在食物假定为一个萤火虫j的所在位置,符合条件j:di,j(t) <rdi(t);li(t) <lj(t),则确定找到食物(同伴),依据确定的食物(同伴)可得出更新后的荧光素浓度,如果不能保证li(t+1)≤li(t),则认为先前位置已是最好觅食地,萤火虫位置不移动;如果觅食次数超过N次,没有找到符合条件的食物(同伴),则认定当前位置已是最好的觅食地,位置不再移动。当Ni(t)为非空集:萤火虫依据概率pij(t)在集合Ni(t)内选择萤火虫j,得出调整后的移动步长和新的移动位置,然后判断li(t+1)≤li(t)是否成立,如果是则进行位置移动,否则不移动。
为了测试觅食次数N对算法性能的影响,本文把该值分别设置为5个不同的值对同一函数的迭代值进行对比。测试函数如下:
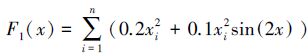
测试结果如图 2所示,从图中可知,该值越小越易陷入局部最优,但是该值增大后并不能保证提高算法搜索精度,如图 2(a)中觅食次数N=10时算法对函数的迭代精度最高,而图 2(b)中觅食次数N=10、15和30时,算法对函数的迭代精度相当,其中精度最高是觅食次数为N=10时,因此在下面算法试验对比分析中,将觅食次数设置为10。

|
| 图 2 觅食次数为不同值时函数迭代值对比 Fig. 2 Iterative value contrast of different foraging times |
GSO算法、PSO算法(粒子群算法)都属于随机优化算法,刘洲洲等[9]和张慧斌等[10]分别对2种算法的收敛性给出了分析证明,他们依据的是Solis[11]给出的随机优化算法收敛性判定标准。
为了分析FA-GSO算法的收敛性,本文参考Solis提出的判定标准,给出分析证明。
条件 1 f(D(x,ξ))≤f(x),并且如果ξ∈S,则有f(D(x,ξ))≤f(ξ)。其中,f和S分别为目标函数和可行解空间,D(x,ξ)为算法第t+1次的迭代结果。
条件 2 如果∀D∈S,v(D)>0,并且$\prod\limits_{k = 0}^\infty {}$(1-μk(D))=0。其中,v(D)为D的勒贝格测度,μk(D)为算法第k次迭代解的概率测度。
收敛判定定理 设函数f可测,搜索空间S是Rn上的可测度子集,如果算法满足条件1和条件2,则有limk→$\mathop {\lim }\limits_{k \to \infty }$p(xk∈S*)=1,即算法以概率1收敛于全局最优值。其中S*是全局最优点集合,xk是算法迭代过程中的数列。
定理 FA-GSO算法以概率1收敛于全局最优解。
证明 根据1.2和2.1小节的描述,由于算法的步长是自适应调整的,依据是式(5)、(6),并且保证了无同伴萤火虫的优化搜索,通过判断萤火虫前后2次的荧光素大小确定位置是否移动,依据是式(3)和觅食策略,所以可以得出对于ξ∈S,有f(D(x,ξ))≤f(x),即满足条件1。
假设L为萤火虫i在第t次迭代过程中搜索解支撑集,随着算法迭代次数的增加,出现萤火虫的聚集现象并且也可能出现萤火虫“不动”的现象,v(L)逐渐变小,使的v($\bigcup\limits_{i = 1}^n {}$L∩S) <v(S),即不满足条件2。
另改进的算法使得萤火虫都可以执行觅食行为,当觅食次数N→∞,则有0 <$\sum\limits_{i = 1}^n {}$μ(D)≤1,$\bigcup\limits_{i = 1}^n {}$L=S,进一步可得μ$\mathop {\lim }\limits_{n \to \infty }$D(xn)=D(S*)}=1,即$\prod\limits_{k = 0}^\infty {}$(1-μk(D))=0,所以满足条件2。
综上可得:$\mathop {\lim }\limits_{n \to \infty }$p(xn∈S*)=1,由收敛判定定理可知FA-GSO算法以概率1收敛于全局最优解,证毕。
2.3 FA-GSO实现步骤综上,基于觅食行为的自适应步长人工萤火虫算法步骤描述如下:
1)初始化萤火虫群体和参数。将n只萤火虫随机地分布在搜索空间m维中,同时为每只萤火虫初始化以相同的荧光素l0和感应半径r0,初始化最大移动步长smax,最小移动步长smin,萤光素挥发系数ρ,觅食次数N,萤光素更新率γ以及设定迭代次数Nmax等,形成初始萤火虫群;
2)执行FA-GSO算法搜索。
对初始化的萤火虫个体,分别执行以下操作:
a)对每一个萤火虫i按式(1)更新荧光素的值,判断li(t+1)≤li(t)是否成立,如果是则转向b),否则在转向b)前,令xi(t+1)=xi(t)。
b)在动态决策域半径rdi(t)内,求萤火虫i的邻域集合Ni(t)。
c)选择t+1时刻移动的方向:
若Ni(t)不为空集,利用式(2)计算向邻域内萤火虫j的移动概率pij(t),其中0 <rdi(t) <rs,rs为萤火虫个体的感知半径,并采用轮盘赌法则选择邻域内萤火虫个体,确定为下一时刻萤火虫的移动方向;
若Ni(t)为空集,在其动态决策半径rdi(t)内执行觅食行为,设定觅食次数最大值为N次,每次觅食意味着寻找下次迭代移动方向,如果存在食物假定为一个萤火虫j的所在位置,符合条件j:di,j(t) <rdi(t);li(t) <lj(t),则确定找到食物(同伴);如果觅食次数超过N次,没有找到符合条件的食物(同伴),则认定当前位置已是最好的觅食地,位置不再移动。
d)根据式(5)计算每个萤火虫的荧光因子,并用式(6)计算动态移动步长。
e)萤火虫进行位置移动,根据式(3)更新位置;
f)根据式(4)更新萤火虫的动态感知范围。
3)判断是否达到指定的迭代次数,如果达到则转向步骤4),否则转向2)。
4)输出结果,程序结束。
3 实验结果与分析为了验证所设计的算法的有效性。选取4个标准测试函数进行验证,并与GSO算法以及自适应步长GSO算法(A-GSO)进行比较。这4个常用的测试函数如下。
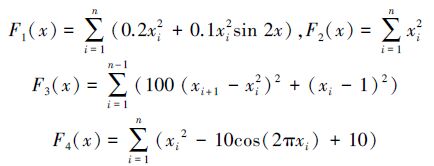
实验的程序运行环境为:处理器Intel i3 CPU M380,主频为2.53 GHz,内存2 GB,操作系统为Windows XP,集成开发环境为Visual Studio 2005,算法用VB.NET编写。
算法参数初始化为萤火虫数量n为50,荧光素更新率r为0.6,荧光素挥发系数p为0.4,初始荧光素大小为5,感知范围为10,初始最小步长为0.01,最大步长为1,b=0.08,nt=5,觅食次数为10,最大迭代次数为300。对于上述4个标准测试函数进行试验,维数为10。
表 1列出4个算法对选定的标准测试函数求解所得到的最优值、最差值、平均值和平均迭代次数比较,表中的平均迭代次数为10次独立实验所得到的迭代次数平均值。从表 1中的数据对比中可以看到,FA-GSO算法平均通过42次迭代就找到了函数F1(x)最小值,而其他2种算法都没有找到最小值,而A-GSO的最优解要好于GSO迭代的最优解。对比3种算法搜索其他3个函数的最优解看,FA-GSO的最优解也是最接近最小值,A-GSO的最优解好于GSO搜索的最优解,观察另外2个指标,即最差解和平均解的数据对照,也可以得出类似的结论。所以可以看出FA-GSO算法在搜索函数极值的最优解、最差解以及平均解都要比另外3种算法有了一定程度上的提高,表明FA-GSO算法在收敛精度上要优于其他2种算法。观察表中的平均迭代次数,对比3个算法分别迭代给定的每个函数,可以看到FA-GSO算法平均迭代次数要少于其他2个算法,表明FA-GSO算法在收敛速度上要优于另外2种算法。
| 测试函数 | 算法 | 最优解 | 最差解 | 平均解 | 平均迭代次数 |
| F1(x) | GSO | 0.235 | 3.360 | 2.370 | 85 |
| A-GSO | 0.081 | 2.760 | 1.640 | 72 | |
| FA-GSO | 0.000 | 0.524 | 0.065 | 42 | |
| F2(x) | GSO | 0.256 | 3.560 | 2.130 | 75 |
| A-GSO | 0.102 | 1.560 | 0.850 | 56 | |
| FA-GSO | 0.014 | 0.096 | 0.067 | 53 | |
| F3(x) | GSO | 1.95 | 10.58 | 6.54 | 106 |
| A-GSO | 0.41 | 3.57 | 2.65 | 80 | |
| FA-GSO | 0.15 | 1.56 | 0.89 | 61 | |
| F4(x) | GSO | 0.16 | 2.67 | 2.130 | 81 |
| A-GSO | 0.12 | 2.92 | 1.360 | 77 | |
| FA-GSO | 0.03 | 0.83 | 0.482 | 46 |
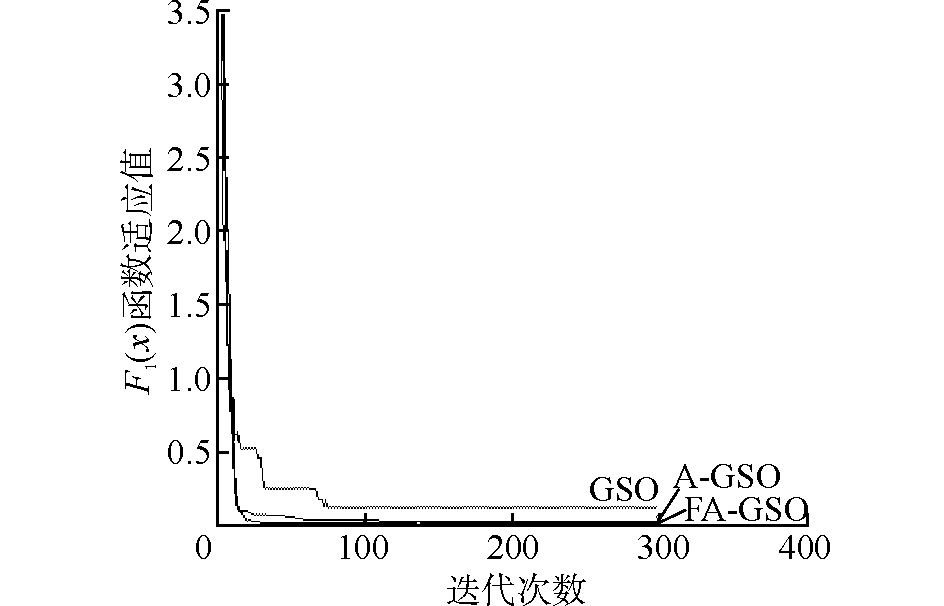
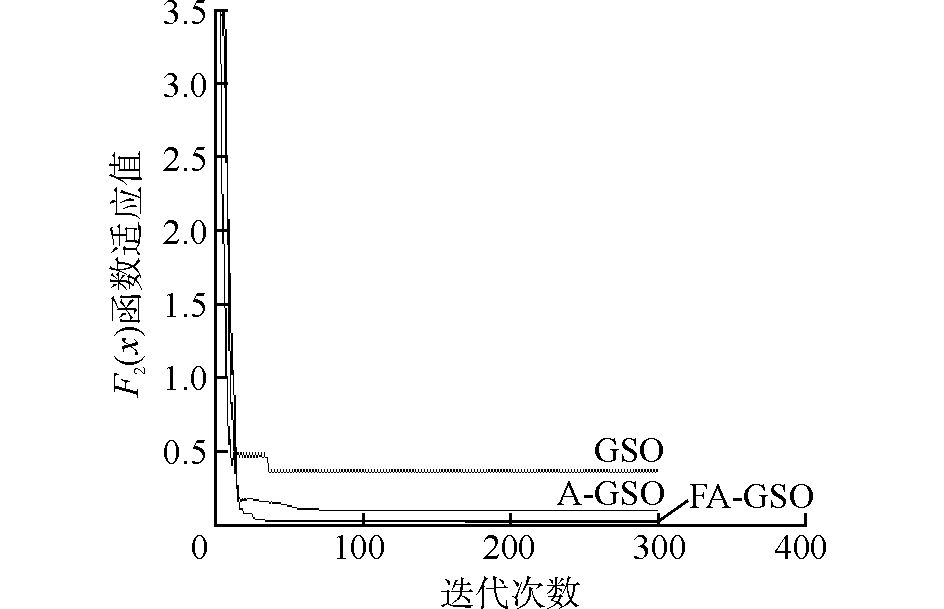
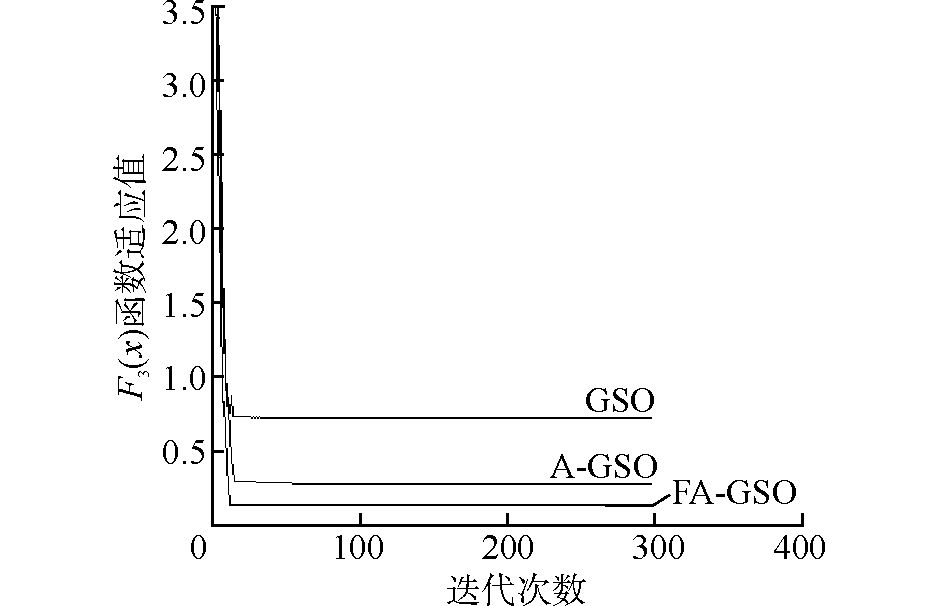
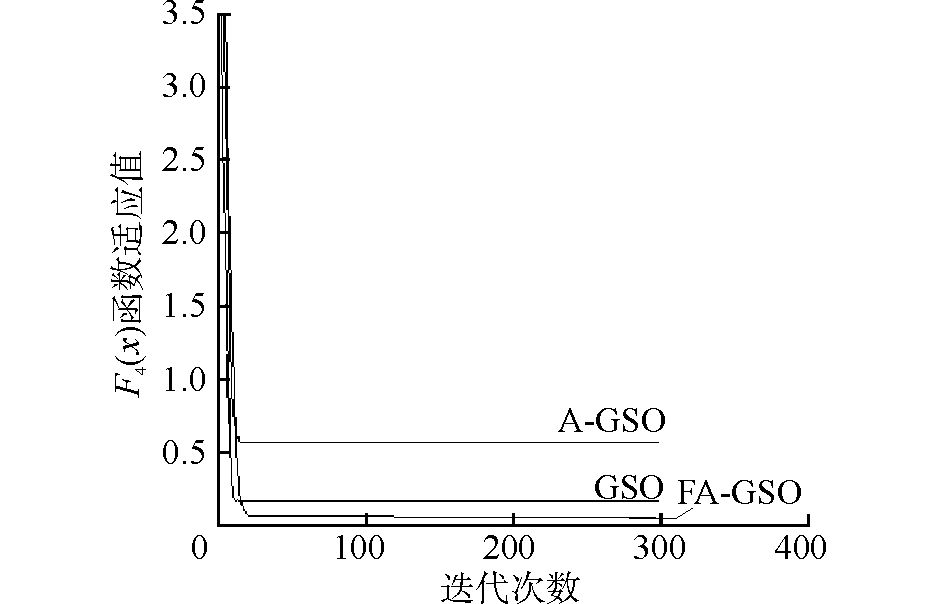
从图 3~6中看到,4个函数的FA-GSO算法迭代曲线很接近横轴,即函数适应值很接近最小值,迭代精度要好于另外2种算法,而且算法能够找到最优解前的迭代次数也是最少的。此外,观察GSO算法在迭代函数F1(x)和F2(x)时都发生了适应值曲线的震荡现象,验证了固定步长带来的寻优缺陷,而A-GSO和FA-GSO算法曲线都相对稳定。从图 6中还可以看到A-GSO算法在迭代函数F4(x)时所搜索的最优解并没有好于GSO,但是FA-GSO的最优解还是三者中精度最高的,说明搜寻机制改进后的算法在寻优精度方面有着较高的稳定性。从图中可以看出FA-GSO算法寻优比较稳定和快速。综上所述,FA-GSO算法在函数搜索精度以及速度2个关键方面的性能有着明显的改进,从而有助于提高寻优问题的求解效率。
|
| 图 3 F1(x)函数值随3个算法迭代曲线 Fig. 3 Iterative values graph of F1(x) tested by the three algorithms |
|
| 图 4 F2(x)函数值随3个算法迭代曲线 Fig. 4 Iterative values graph of F2(x) tested by the three algorithms |
|
| 图 5 F3(x)函数值随3个算法迭代曲线 Fig. 5 Iterative values graph of F3(x) tested by the three algorithms |
|
| 图 6 F4(x)函数值随3个算法迭代曲线 Fig. 6 Iterative values graph of F4(x) tested by the three algorithms |
针对GSO和A-GSO算法存在的不足,为了有效避免算法过快陷入局部最优和寻优值的震荡现象,通过改进算法的迭代机制,在提出的FA-GSO算法中引入觅食行为并自适应调整移动步长进一步改善了局部搜索能力。本文采用3种算法对标准测试函数的试验,对照相关迭代指标并分析后得出FA-GSO算法寻优结果优于GSO和A-GSO算法,改进的算法是有效的,提高了寻优稳定性、收敛速度和求解精度,从而改善了算法的迭代效率。未来将要做的工作内容,可以在算法参数的优化分析及算法的应用(如交通信号和交通模型的优化等)做进一步研究和探索。
| [1] | LIAO Wenhua, KAO Yucheng, LI Yingshan. A sensor deployment approach using glowworm swarm optimization algorithm in wireless sensor networks[J]. Expert Systems with Applications, 38(10): 12180-12188. |
| [2] | KRISHNANAND K N D, GHOSE D. Glowworm swarm based optimization algorithm for multimodal functions with collective robotics applications[J]. Multiagent and Grid Systems, 2006, 2(3) 209-222. |
| [3] | KRISHNANAND K N, GHOSE D. Glowworm swarm optimization for simultaneous capture of multiple local optima of multimodal functions[J]. Swarm Intelligence, 2009, 3(2): 87-124. |
| [4] | YANG Yan, ZHOU Yongquan, GONG Qiaoqiao. Hybrid artificial glowworm swarm optimization algorithm for solving system of nonlinear equations[J]. Journal of Computational Information Systems, 2010, 6(10) 3431-3438. |
| [5] | 黄正新, 周永权. 自适应步长萤火虫群多模态函数优化算法[J]. 计算机科学, 2011, 38(7): 220-224.HUANG Zhengxin, ZHOU Yongquan. Self-adaptive step glowworm swarm optimization algorithm for optimizing multimodal functions[J]. Computer Science, 2011, 38(7): 220-224. |
| [6] | 欧阳喆, 周永权. 自适应步长萤火虫优化算法[J]. 计算机应用, 2011, 31(7): 1804-1807.OUYANG Zhe, ZHOU Yongquan. Self-adaptive step glowworm swarm optimization algorithm[J]. Journal of Computer Applications, 2011, 31(7): 1804-1807. |
| [7] | KRISHNANAND K N D, GHOSE D. Glowworm swarm optimization: a new method for optimizing multi-modal functions[J]. Computational Intelligence Studies, 2009, 1(1): 93-119 |
| [8] | 张军丽, 周永权. 人工萤火虫与差分进化混合优化算法[J]. 信息与控制, 2011, 40(5): 608-613.ZHANG Junli, ZHOU Yongquan. A hybrid optimization algorithm based on artificial glowworm swarm and differential evolution[J]. Information and Control, 2011, 40(5): 608-613. |
| [9] | 刘洲洲, 王福豹, 张克旺. 基于改进萤火虫优化算法的WSN 覆盖优化分析[J]. 传感技术学报, 2013, 26(5): 675-682.LIU Zhouzhou, WANG Fubao, ZHANG Kewang. Performance analysis of improved glowworm swarm optimization algorithm and the application in coverage optimization of WSNs[J]. Chinese Journal of Sensors and Actuators, 2013, 26(5): 675-682. |
| [10] | 张慧斌, 王鸿斌, 胡志军. PSO算法全局收敛性分析[J]. 计算机工程与应用, 2011, 47(34): 61-63.ZHANG Huibin, WANG Hongbin, HU Zhijun. Analysis of particle swarm optimization algorithm global convergence method[J]. Computer Engineering and Applications, 2011, 47(34): 61-63. |
| [11] | SOLIS F J, WETS R J B. Minimization by random search techniques[J]. Mathematics of Operations Research, 1981, 6(1): 19-30. |



