同步定位与地图构建(simultaneous localization and mapping,SLAM)最先是由Smith等提出来的[1],指移动机器人从一个未知的位置出发,在运动过程中利用传感器对环境的观测递增地建立地图,同时根据已建立的地图同步确定自己的位置。十多年来,SLAM问题仍然是机器人研究领域的热点[2]。
目前SLAM问题的解决方法以概率估计为主,主要分为基于卡尔曼滤波(KF)的算法和基于粒子滤波(PF)的算法。其中,基于EKF的SLAM算法[3]的研究最早开始于1986年,虽然计算速度快,但此类算法存在难以解决的数据关联问题,且计算量过大、精度不高。UKF不需要进行雅可比矩阵计算、计算量小。而在实际应用时,系统噪声相关信息的不确定性都会影响UKF滤波的精度,并且主要参数和滤波增益不能在线调整,缺乏自适应能力[4]。近年来,基于粒子滤波的方法正逐渐成为研究SLAM的热点。相对于KF及其衍生算法,PF的优点在于能有效处理非线性非高斯分布的状态估计问题。Doucet等[5]提出有效解决SLAM问题的Rao-Blackwellized粒子滤波器(RBPF)方法。每一个粒子代表机器人一种可能的运动轨迹,同时每一个粒子都具有自己的全局地图,它们和该粒子的轨迹相对应。因此该算法能够较好地近似移动机器人位姿和环境地图的联合概率密度。但当粒子数目增多、环境地图的尺寸增大时,算法会占用大量的内存空间,而且重采样过程中,全局地图进行拷贝需要占用大量的内存空间[6]。因此,降低计算复杂度以及减少构建精确地图所需的粒子数成为此类方法需要重点解决的问题。Griseti等[7]通过改进建议分布和引入自适应重采样机制提高该算法的执行效率。
2010年Willow Garage公司发布了开源机器人操作系统(robot operating system,ROS),由于其具有点对点设计、不依赖编程语言、开源等优点,很快在机器人领域展开学习和使用ROS的热潮[8]。在ROS中,Griseti等的算法被制作成一个名为Gmapping的SLAM功能包[9],使用激光测距仪可以建立精度较高的二维栅格地图,但其实时性仍有待提高。本文在此基础上提出了一种降低复杂度的改进算法,在RBPF的卡尔曼更新步骤中,从一组粒子里选取一个代表粒子进行更新,避免计算所有粒子。通过在配有激光测距仪的Pioneer III机器人上的实验来验证该算法的有效性。
1 RBPF与地图构建 1.1 Rao-Blackwellized变换在SLAM问题中,Rao-Blackwellized变换可理解为将联合后验概率分解为对路径的后验概率和在给定路径的情况下对地图的后验概率[10]。具体分解如式(1):

如1.1小节所述,RBPF可以分为粒子滤波和卡尔曼滤波两部分。
1.2.1 粒子滤波部分粒子滤波是一种马尔可夫链蒙特卡罗算法,用一系列样本(粒子)来估计未知状态[11]。通过重要性采样原则,第i个样本的概率可以用重要性权值ωti表示。
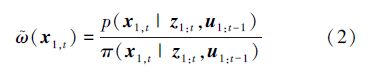
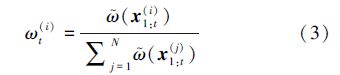
归一化权值ωt(i)与样本{x1:t(i),m(i)}共同决定后验概率分布p(xt,m|z1:t,u1:t-1)。假定用N个带有权值的样本{(x1:t(i),m(i)),ωt(i)}i=1N表示后验分布p(x1:t,m|z1:t,u1:t-1),则
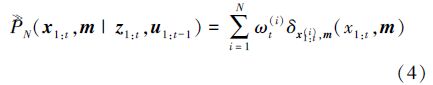

由此,地图的后验概率可估算为
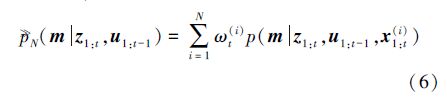
标准RBPF算法中的粒子滤波由以下3步组成,其中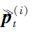 表示第i个粒子。
表示第i个粒子。
1)蒙特卡罗步骤:RBPF算法中的蒙特卡罗步骤包括从先验分布中采样:

 ,但每个粒子
,但每个粒子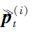 都包含了轨迹和地图的信息,分别由
都包含了轨迹和地图的信息,分别由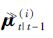 和
和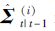 表示。
表示。
2)序贯重要性采样步骤:包括计算式(5)中的p(x1:t|z1:t,u1:t-1)。如果把先验分布当作重要性函数,例如π(x1:t|z1:t,u1:t-1)=P(xt|xt-1),从而可以递归计算:

 为相似函数。在算法实现中,t-1时刻重采样后如果传播粒子权值相同,可以省去ωt-1i。
为相似函数。在算法实现中,t-1时刻重采样后如果传播粒子权值相同,可以省去ωt-1i。
3)重采样步骤:舍弃低权值粒子,保留高权值粒子。
1.2.2 卡尔曼滤波部分
通过粒子滤波部分采样 之后,卡尔曼滤波负责更新地图m的均值和方差。
之后,卡尔曼滤波负责更新地图m的均值和方差。

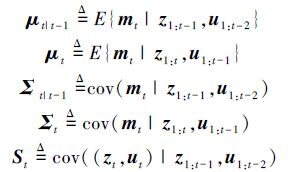
通过在均值和方差更新步骤使用卡尔曼滤波器,RBPF算法的估算精度能得到较大提高。然后,RBPF算法需要对每一个粒子使用卡尔曼滤波器,当有大量粒子时计算复杂度会急剧增加。
2 改进RBPF算法标准RBPF中需对每一个存活粒子i,pt(i)进行卡尔曼更新,包括重复计算μt(i)和Σt(i),然后再循环步骤重复计算逆矩阵St-1(i),这将导致计算量巨大。在粒子滤波部分的重采样步骤中,高权值粒子决定机器人更可能的位置。这一步骤中,粒子聚集在一些特殊位置。然后在RB变换中,粒子估计的状态是离散的。这说明聚集在离散状态的粒子群分布在有限空间中。因此,所有粒子的统计特性,例如μt(i)和Σt(i)是一致的,只需其中之一作为代表来进行卡尔曼滤波步骤。最终改进RBPF算法只需用K个卡尔曼滤波器(K<N)计算μt(i)和Σt(i)更新不同位置的粒子。
通过在必要时更新μt(i)和Σt(i)并在同一粒子群中重复使用,在粒子数中等或者大量时,例如100≤N≤1 000,时间和计算消耗能明显减小。当粒子数相对小时,例如N≤10,改进RBPF算法相对标准RBPF的优势不明显。2种算法对比如下:
1)标准RBPF的卡尔曼更新步聚:

2)改进RBPF的卡尔曼更新步聚:
for pt(1),更新均值μt(1)和方差Σt(1)
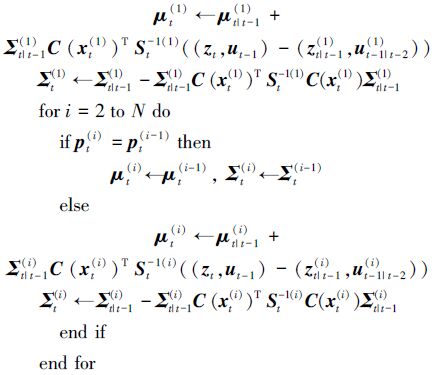
此外,建议分布采用文献[7]中的

改进算法流程示意如图 1所示。在t-1时刻,采样阶段进行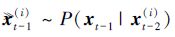 得到无权重粒子
得到无权重粒子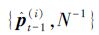 。重要性采样阶段得到带权重的粒子
。重要性采样阶段得到带权重的粒子 。重采样阶段,保留高权重粒子舍去低权重粒子得到{pt-1(i),N-1}。减小复杂度过程,只负责更新不同位置的粒子,使用一组K(K≤N)个卡尔曼滤波器计算μt(i)、Σt(i),因此减少了卡尔曼更新的计算量。最后,在t时刻采样阶段进行
。重采样阶段,保留高权重粒子舍去低权重粒子得到{pt-1(i),N-1}。减小复杂度过程,只负责更新不同位置的粒子,使用一组K(K≤N)个卡尔曼滤波器计算μt(i)、Σt(i),因此减少了卡尔曼更新的计算量。最后,在t时刻采样阶段进行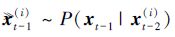 得到
得到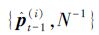 。
。

|
| 图 1 改进RBPF算法流程 Fig. 1 The flow chart of improved RBPF algorithm |
实验平台由装载URG-04LX激光测距仪的Pioneer III-DX机器人、配有Intel双核、CPU 2.19 GHz、内存1.96 GB的笔记本电脑组成,笔记本电脑安装Ubuntu 12.04操作系统与Groovy版本ROS,由笔记本键盘控制机器人的运动,如图 2所示。实验环境为重庆邮电大学信息无障碍工程研发中心一楼,如图 3所示。

|
| 图 2 实验硬件平台 Fig. 2 Experiment hardware platform |

|
| 图 3 实验环境 Fig. 3 Experiment environment |
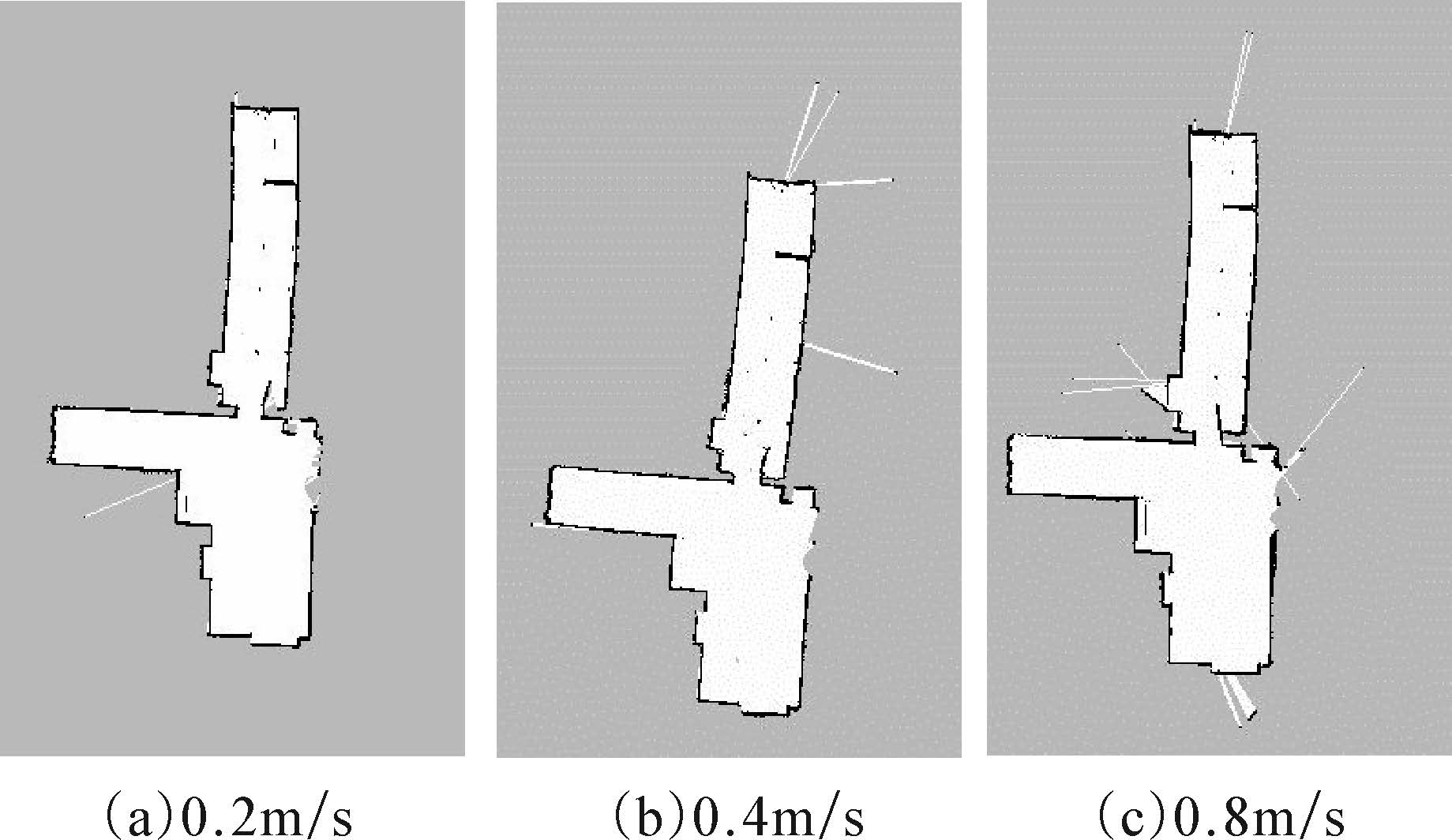
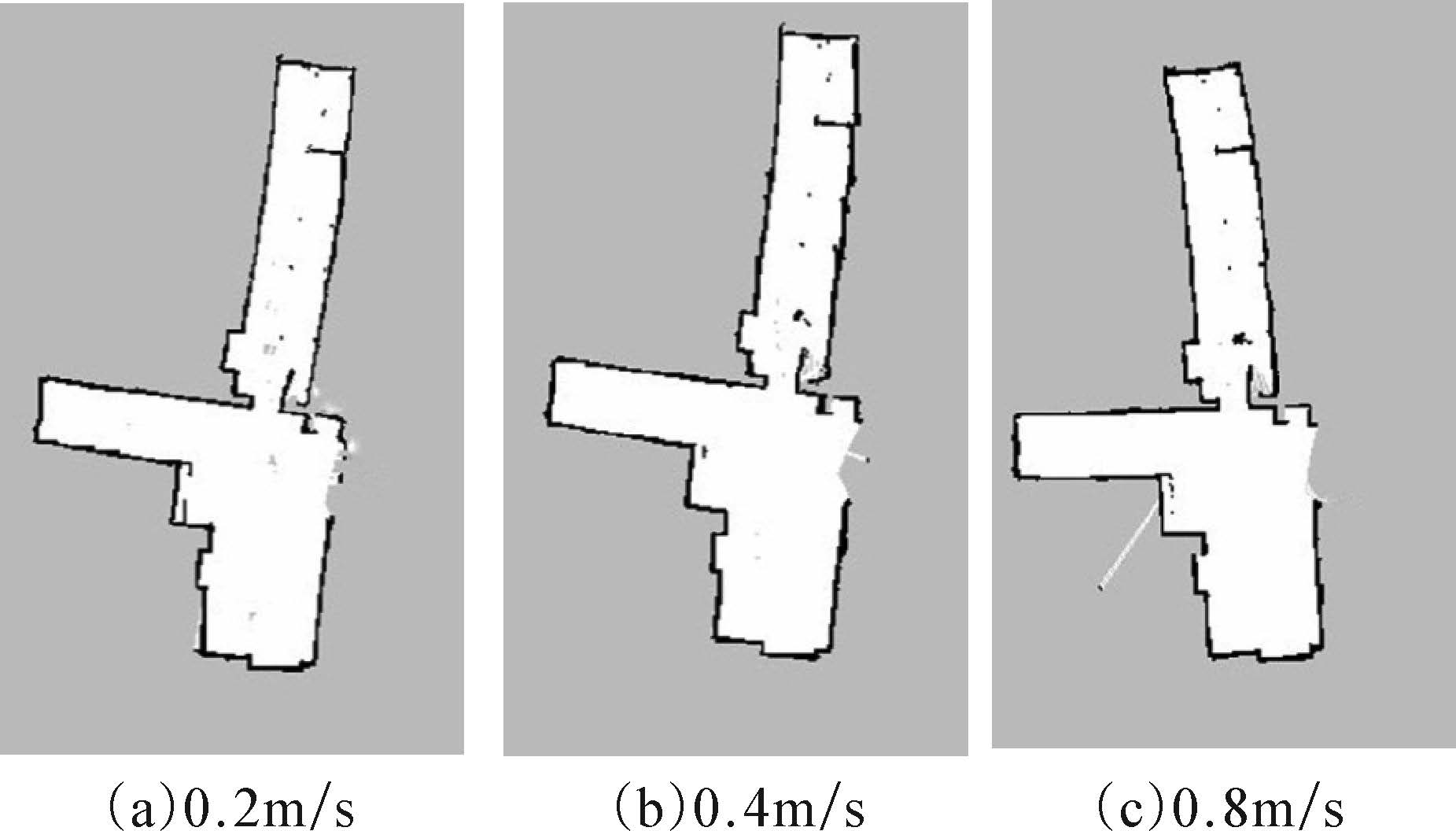
在同步定位与地图构建中,总时间消耗与机器人的运动速度和环境大小有关,具体算法的时间消耗难以确定。但可以通过控制机器人的运动速度来衡量算法的实时性:如果算法复杂度过大,计算所需时间因此较长,较快的运动速度将导致地图的精度下降,需放慢运动速度以保证地图精度;如果算法复杂度较小,计算所需时间因此较小,较快的运动速度下也能保证地图精度。2种算法均需120个粒子,每种算法每种速度作为1组进行10次实验,共进行60次实验。每组第1次实验中使用机器人实地运行,得出地图同时将观测数据(里程计数据与激光数据)记录在bag文件中,其余9次实验使用该bag文件中的数据进行仿真,得出相应地图。bag文件为ROS特有的文件格式,可以将各类数据信息存储在一个文件内,在调试算法过程中使用广泛。使用bag文件进行算法调试可以保证每组实验的数据一致,减小误差。实验结果显示每组均出现共同特征,选取代表性结果进行对比。图 4和图 5为不同运动速度下Gmapping算法与改进算法所绘地图。
|
| 图 4 3种不同速度下Gmapping算法所绘地图 Fig. 4 Maps built with Gmapping in three different velocities |
|
| 图 5 3种不同速度下改进算法所绘地图 Fig. 5 Maps builts with improved algorithm in three different velocities |
实验表明,2种算法随着机器人运动速度的增加,均出现栅格误差增大、地图质量下降的情况。在0.2 m/s低速运动时,2种方法均能创建稳定的地图;以0.4 m/s运动时,Gmapping算法开始出现误差,地图出现不确定性,改进算法没有出现误差;以0.8 m/s运动时,Gmapping所绘地图误差增多,改进算法也出现误差,但整体效果明显强于前者。此外,改进算法在不同速度下所建地图更为稳定,边缘更加清晰。
4 结束语本文提出了一种改进RBPF算法用于移动机器人的同步定位与地图构建,通过卡尔曼滤波更新某一特定状态一组粒子中的代表粒子,在必要时更新其均值和方差,并在同一粒子群中重复使用,以降低复杂度提高系统实时性。在近年来国外使用越来越广泛的机器人操作系统平台下进行实验,实验结果验证了其有效性。在后续工作中,将致力于量化降低的复杂度以及所提高的实时性。
| [1] | SMITH R, SELF M, CHEESEMAN P. Estimating uncertain spatial relationships in robotics[M]//COX I J, WILFONG G T. Autonomous Robot Vehicles. New York: Springer, 1990: 167-193. |
| [2] | DISSANAYAKE G, HUANG S, WANG Z, et al. A review of recent developments in simultaneous localization and mapping[C]//6th International Conference on Industrial and Information Systems (ICIIS). Kandy, Sri Lanka, 2011: 477-482. |
| [3] | SMITH R C, CHEESEMAN P. On the representation and estimation of spatial uncertainty[J]. The International Journal of Robotics Research, 1986, 5(4): 56-68. |
| [4] | 张文玲, 朱明清, 陈宗海. 基于强跟踪UKF的自适应 SLAM 算法[J]. 机器人, 2010, 32(2): 190-195. ZHANG Wenling, ZHU Mingqing, CHEN Zonghai. An adaptive SLAM algorithm based on strong tracking UKF[J]. Robot, 2010, 32(2): 190-195. |
| [5] | DOUCET A, De FREITAS N, MURPHY K, et al. Rao-Blackwellised particle filtering for dynamic Bayesian networks[C]//Proceedings of the Sixteenth Conference on Uncertainty in Artificial Intelligence. San Francisco, USA, 2000: 176-183. |
| [6] | QU Liping, WANG Hongjian. An overview of robot SLAM problem[C]//International Conference on Consumer Electronics, Communications and Networks (CECNet). Xianning, China, 2011: 1953-1956. |
| [7] | GRISETTI G, STACHNISS C, BURGARD W. Improved techniques for grid mapping with Rao-Blackwellized particle filters[J]. Robotics, 2007, 23(1): 34-46. |
| [8] | 张建伟, 张立新, 胡颖, 等. 开源机器人操作系统—ROS[M]. 北京: 科学出版社, 2012: 1-6. |
| [9] | GERKEY B. Gmapping.[EB/OL].[2010-08-05]. http://wiki.ros.org/slam_gmapping. |
| [10] | GRISETTI G, STACHNISS C, BURGARD W. Improving grid-based slam with Rao-Blackwellized particle filters by adaptive proposals and selective resampling[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation. Barcelona, Spain, 2005: 2432-2437. |
| [11] | DOUCET A, De FREITAS N, GORDON N. An introduction to sequential Monte Carlo methods[M]//DOUCET A, DE FREITAS N, GORDON N. Sequential Monte Carlo Methods in Practice. New York: Springer, 2001: 3-14. |
| [12] | De FREITAS N. Rao-Blackwellised particle filtering for fault diagnosis[C]//2002 IEEE Aerospace Conference Proceedings. Big Sky, USA, 2002, 4: 1767-1772. |



