机器人同时定位与地图构建问题(simultaneous localization and mapping,SLAM)和目标跟踪问题(object tracking,OT)在机器人学界通常被作为2个独立问题加以研究,而对于某些实际任务,需要将SLAM和OT问题作为耦合问题来处理,例如未知环境下目标跟踪任务[1]、未知环境下机器人围捕任务[2,3]。此类任务要求机器人在未知环境条件下对目标进行定位和追踪,也就是说,算法需要对机器人状态、环境特征状态以及目标状态进行同步估计。Wang等[4]首先对该问题进行了研究并提出一种基于扫描点匹配的解决方法,由于该方法采用的是ICP(iterative closest point)匹配算法,因此无法描述机器人和目标的不确定性和相关性,并且存在累积误差[5, 6, 7]。Vu等[1]运用全局邻域法(global nearest neighborhood,GNN)进行动态物体检测,并用EKF对运动物体进行跟踪。伍明等[8]提出了基于卡尔曼滤波框架的单目标跟踪算法,实现了机器人同时定位、地图构建与多目标跟踪(simultaneous localization,mapping and multi-objects tracking,SLOMMOT)的对象状态耦合估计。现有上述方法并未考虑机器人未知环境下多目标跟踪问题,然而对于该问题的研究能够有效扩展已有方法的应用前景,使相关算法更具实用价值。
针对SLOMMOT问题提出了一种基于联合概率数据关联(joint integrated probabilistic data association,JIPDA)的粒子滤波算法,算法采用Rao-Blackwellized粒子滤波框架,并利用IPDA解决多目标跟踪问题。首先对未知环境下机器人多目标跟踪问题的相关模型进行描述,然后给出基于联合概率数据关联粒子滤波算法的具体处理过程,最后通过仿真实验验证算法对机器人状态、多目标状态和环境特征状态估计的有效性,并分析粒子数对机器人和目标定位准确性的影响。
1 问题描述及联合概率数据关联多目标数据关联目的是确定目标观测值和每个目标的对应关系,假设在k时刻,系统得到nk个目标观测值,记为
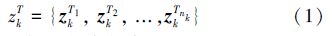
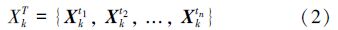
联合概率数据关联滤波由Musicki等[9]首先提出,JIPDA能够解决多目标跟踪问题,该方法对每个目标产生一个跟踪滤波器,每次迭代时考虑所有目标观测值-跟踪滤波器组合情况,并用全部目标观测值对每个跟踪滤波器进行更新。
假设关联事件θj,i代表关联关系(j,i)∈{1,2,...,nk}×{1,2,...,n}发生,即目标观测值分量zkTj和目标ti状态Xkti相对应。首先计算观测值zkTj由目标ti引发的后验概率:
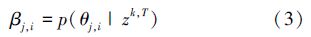
假设该估计问题为马尔可夫过程,对式(3)进行如下推导:
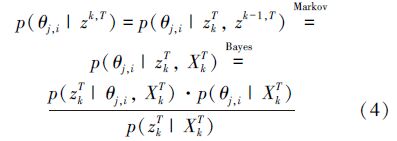
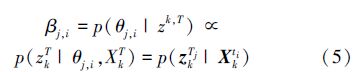
由贝叶斯定理可得目标ti在k时刻状态估计为


式(7)表示目标状态的预测过程。由于不能确定目标观测值和目标的对应关系,此处利用加权和的形式来表示式(7),即

为了解决未知环境下机器人多目标追踪问题,在基于Rao-Blackwellised粒子滤波的单目标SLAMOT算法基础上,修改粒子群结构如下:

机器人单目标Rao-Blackwellised粒子滤波运用传统粒子滤波完成机器人状态估计,并对每一个粒子包含的标志柱、目标状态均值和协方差运用EKF进行估计。当涉及多个目标的追踪时,需要运用联合概率数据关联方法对原算法进行改进。
未知环境下多目标跟踪算法粒子权值目标部分推导如下:
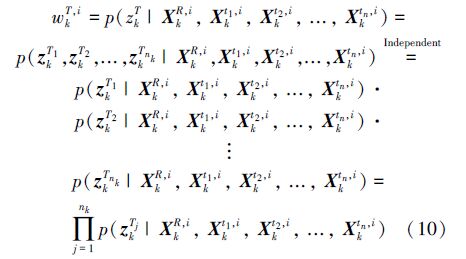
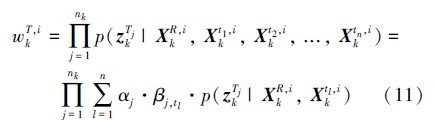
 为归一化因子,βj,tl由式(5)给出。
为归一化因子,βj,tl由式(5)给出。
最后介绍目标更新过程,利用式(8)对粒子i对应的tm目标状态进行更新:
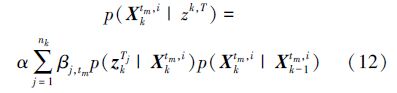
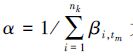 为归一化因子,Xktm,i代表k时刻粒子i包含的目标tm状态,zkTj代表k时刻对目标的第j个观测值,βj,tm同样由式(5)给出。式(12)的p(zkTj|Xktm,i)p(Xktm,i|Xk-1tm,i)部分可以通过EKF得到:首先由目标状态转移函数得到k时刻目标tm的预测状态Xk|k-1tm,i和协方差矩阵Pk|k-1tm,i,之后在更新阶段,利用目标的观测函数和实际目标观测值zkTj对目标预测状态进行矫正,以得到更新的目标状态Xktm,i和协方差矩阵Pktm,i,该过程与单目标跟踪算法类似,参见文献[8],此处不再详细介绍。
为归一化因子,Xktm,i代表k时刻粒子i包含的目标tm状态,zkTj代表k时刻对目标的第j个观测值,βj,tm同样由式(5)给出。式(12)的p(zkTj|Xktm,i)p(Xktm,i|Xk-1tm,i)部分可以通过EKF得到:首先由目标状态转移函数得到k时刻目标tm的预测状态Xk|k-1tm,i和协方差矩阵Pk|k-1tm,i,之后在更新阶段,利用目标的观测函数和实际目标观测值zkTj对目标预测状态进行矫正,以得到更新的目标状态Xktm,i和协方差矩阵Pktm,i,该过程与单目标跟踪算法类似,参见文献[8],此处不再详细介绍。
整个方法的时间复杂度为O(N·lb(M+1)),其中N为粒子个数,M+1为环境特征和机器人个数之和。该计算复杂度为M+1的线性复杂度,因此能够满足计算效率要求。
3 实验结果及分析下面通过仿真实验验证多目标追踪PFJPDA_SLAMOT算法的有效性,并分析粒子数对于机器人和目标定位准确性的影响,实验在MATLAB 7.5环境下进行。
3.1 算法跟踪结果假设运行环境范围为100 m×100 m,机器人同时追踪3个自左向右运动的目标,机器人控制输入噪声为diag(0.3 m,0.0872 rad),目标运动符合定速模型,目标运动不确定系数为0.4。机器人将根据目标位置计算控制量并向目标构成的三角形中心运动。实验共进行20次仿真,其中一次仿真总体结果如图 1所示。

|
| 图 1 PFJPDA_SLAMOT算法多目标跟踪仿真结果 Fig. 1 The results of simulation about multi-object tracking using PFJPDA_SLAMOT |
仿真中粒子数为50,图 1显示了此次运行的总体情况,图 2显示了相应区域的局部放大图,其中实线轨迹代表对机器人和目标的估计轨迹,虚线轨迹代表机器人和目标的实际运动轨迹。线段代表机器人当前对标志柱的观测值。星号代表标志柱的真实分布,标志柱周围的粒子群代表对标志柱位置的粒子群估计。

|
| 图 2 各对象轨迹估计局部区域放大 Fig. 2 Object trajectory in some local areas |
从图 2可见,算法能够较好地对3个目标和机器人进行定位。本次仿真中对机器人位置估计的误差均值和方差分别为0.452和0.117。对目标1位置估计的误差均值和方差分别为0.923和0.353。对目标2位置估计的误差均值和方差分别为1.544和1.235。对目标3位置估计的误差均值和方差分别为1.952和0.554 3。可见,机器人定位精度要高于目标定位精度。仿真发现,算法对于目标跟踪的灵敏度小于对机器人定位的灵敏度,当机器人估计位置和实际位置出现差别时算法能够较快进行调节;但是当目标估计位置和实际位置出现差别时算法调节较慢。该特点从图 1中得以体现,当代表目标实际位置的实线和代表估计位置的虚线出现偏差时往往需要较长的时间,虚线才能重新跟上实线,而代表机器人实际位置的实线和代表估计位置的虚线出现偏差时,只需要很少的时间虚线就能够跟上实线。其原因在于(如式(11)所示)粒子权值目标部分是根据多个目标观测相似度的乘积来确定的,当对一个目标的观测相似度降低时对其他目标的观测相似度不一定下降,那么它们的乘积值不一定变小,这样对于单目标位置估计的粒子群更新就不一定及时,因此算法对目标跟踪灵敏度相比对机器人定位灵敏度来说较低。另外,从图中可见,目标2和目标3在坐标(39,63)处交汇,由于算法采用了联合概率数据关联方法使得对于两目标的跟踪仍能保持准确。
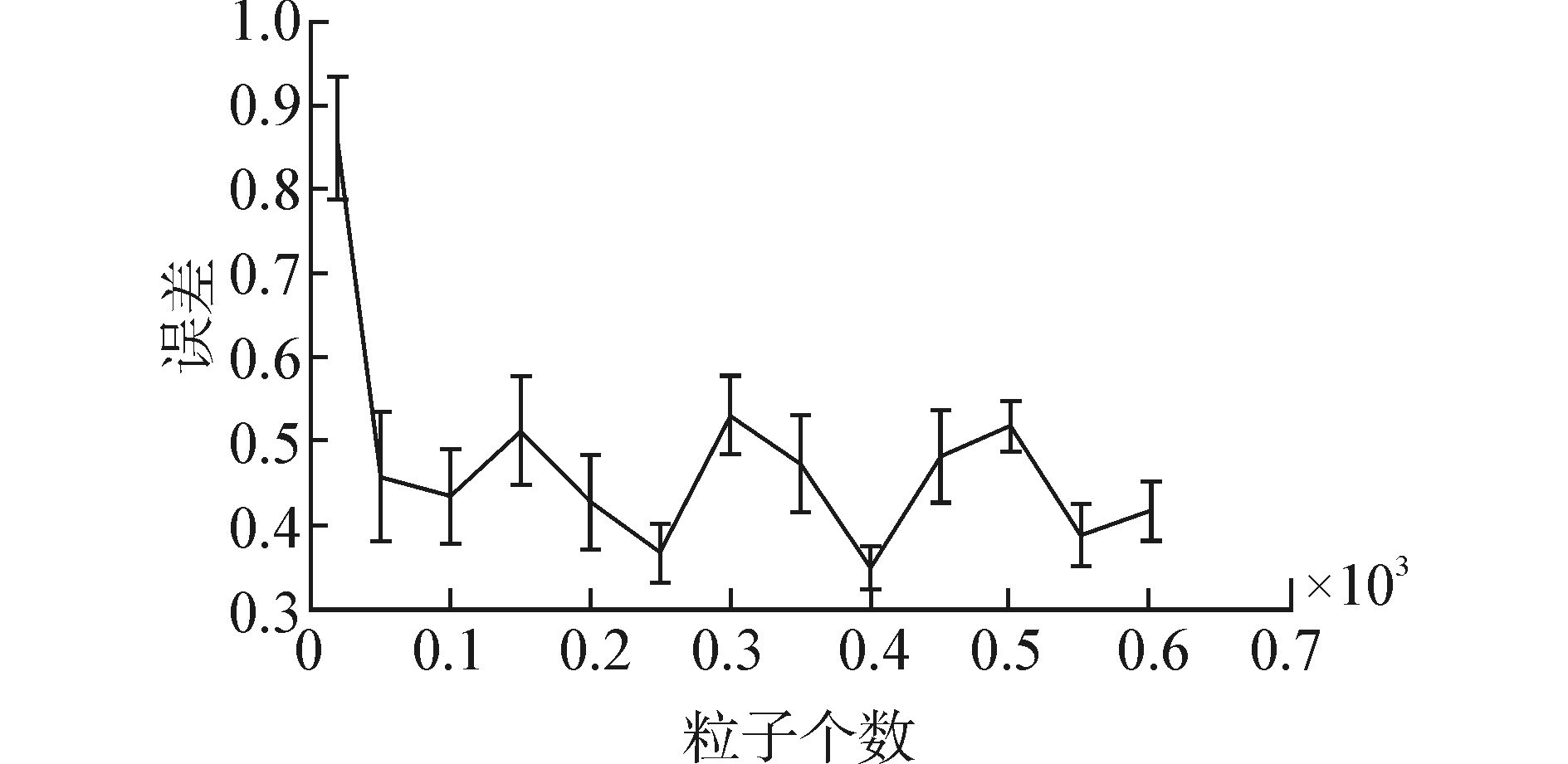
3.2 粒子数量影响本节分析粒子数对机器人和多目标定位的影响,仿真分别采用粒子数为20、50、100、150、200、250、300、350、400、450、500、550和600个,对于每一种粒子数分别进行20次仿真得到的机器人位置误差平均值随粒子数变化如图 3所示。
|
| 图 3 机器人定位精度随粒子数变化情况 Fig. 3 Localization accuracy of robot as a function of the number of particles |
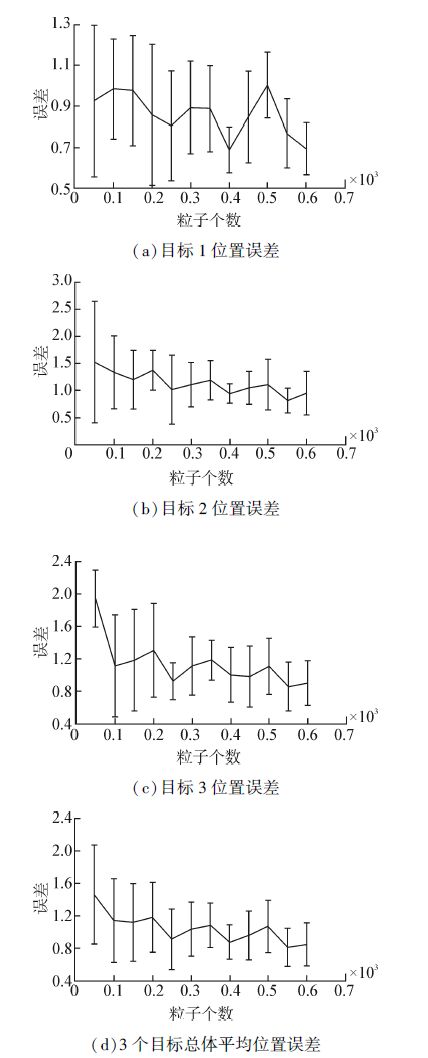
从图 3可知,在粒子数大于50的条件下,机器人定位精度并没有随粒子数的增加而显著提高,其呈现出波动状态。这种现象反映出机器人定位精确度随粒子数量的增加存在一个饱和值,从仿真可见,并非粒子数越多,定位越准确,适当选择粒子数既能够保持高精度又能减少计算量。同样,对应不同粒子数目,算法对3目标定位误差的变化如图 4所示。
|
| 图 4 目标定位精度随粒子数变化情况 Fig. 4 Localization accuracy of objects as a function of the number of particles |
图 4(a)~(c)图分别代表对于目标1、2、3的定位误差的变化情况,图 4(d)为3目标平均定位误差的变化情况。从图中可见,每一个目标的定位精度并不都是随粒子数的增加而提高,目标1在粒子数为500时定位精度最差,造成这种现象的原因同样是因为粒子权值是根据多个目标观测相似度乘积共同产生,当对目标1的定位误差提高时,算法对于目标2、3的定位精度仍然较高,因此粒子对于目标1的调节并不明显。从图 4(d)可见,总体来看对于多目标的综合定位性能,当粒子数目达到一定数量后系统定位精度并未得到进一步提高。
4 结束语本文针对未知环境下机器人多目标跟踪问题,提出了一种基于联合概率数据关联粒子滤波的算法。该算法基于Rao-Blackwellised粒子滤波框架,粒子由机器人状态、多目标状态和环境特征状态联合构成,粒子权值则根据所有目标观测值和跟踪器组合相似度加权和计算得出,该算法能够有效克服多目标观测值对单一目标状态估计的影响,保证较高的目标状态平均估计准确度,仿真实验证明了该算法的有效性。这主要解决了机器人、目标以及环境特征状态估计问题,下一步将在状态估计基础上进行机器人未知环境下导航控制方法研究,另外,利用相关优化方法对粒子群个数进行在线优化选择也将是后续研究重点。
| [1] | VU T D, AYCARD O, APPENRODT N. Online localization and mapping with moving object tracking in dynamic outdoor environments[C]//Proceedings of the IEEE Intelligent Vehicles Symposium. Istanbul, Turkey, 2007: 190-196. |
| [2] | VIDAL R, RASHID S, SHARP C, et al. Pursuit-evasion games with unmanned ground and aerial vehicles[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Seoul, Korea, 2001: 2948-2955. |
| [3] | HUANG Feifei, WANG Long, WANG Qining, et al. Coordinated control of multiple mobile robots in pursuit-evasion games[C]//Proceedings of American Control Conference. St. Louis, USA, 2008: 2861-2866. |
| [4] | WANG C C, THORPE C. Simultaneous localization and mapping with detection and tracking of moving objects[C]//Proceedings IEEE International Conference on Robotics and Automation. Washington, DC, USA, 2002: 2918-2924. |
| [5] | BORRMANN D, ELSEBERG J, LINGEMANN K, et al. Globally consistent 3D mapping with scan matching[J]. Robotics and Autonomous Systems, 2008, 56(2): 130-142. |
| [6] | WANG C C, THORPE C, THRUN S, et al. Simultaneous localization, mapping and moving object tracking[J]. The International Journal of Robotics Research, 2007, 26(9): 889-916. |
| [7] | WAN Kaowei, WANG C C, TON T T. Weakly interacting object tracking in indoor environments[C]//Proceedings of the IEEE International Conference on Advanced Robotics and Its Social Impacts. Taipei, China, 2008: 1-6. |
| [8] | 伍明, 孙继银. 基于扩展式卡尔曼滤波的移动机器人未知环境下动态目标跟踪[J]. 机器人, 2010, 32(3): 334-343.WU Ming, SUN Jigen. Extended Kalman filter based moving object tracking by mobile robot in unknown environment[J]. Robot, 2010, 32(3): 334-343. |
| [9] | MUŠICKI D, EVANS R. Joint integrated probabilistic data association—JIPDA[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3): 1093-1099. |



