多元时间序列是数据挖掘领域中常见的一种数据类型,广泛存在于经济、金融、医疗卫生、电子信息和航空航天等行业中[1].与其他数据类型相比,它有2种高维特性,即时间属性维度和变量属性维度,它们决定了多元时间序列数据的复杂性,同时也影响着数据挖掘技术在多元时间序列数据中的应用性能。为了解决多元时间序列的维灾问题,许多学者提出利用数据降维和特征表示等方法结合相关技术来提高多元时间序列的数据挖掘性能[2, 3]。除了简单运用一元时间序列的降维技术和特征表示外,通常利用数据变换的方法来实现数据处理,达到减噪降冗的效果,例如奇异值分解[4, 5, 6]、独立成分分析[7 ,8]和主成分分析[9, 10]等。其中,主成分分析(principal component analysis,PCA)是多元时间序列数据降维和特征表示中最常用的方法之一[11],它通过对多元时间序列的协方差矩阵进行特征分解,实现数据空间变换得到方差最大的主成分作为原始数据的特征。同时,根据方差大小选择对应的前几个主成分作为多元时间序列的数据特征,从而实现原始多元时间序列的变量属性维度的降维。
在多元时间序列数据挖掘前期任务中,除了进行数据降维和特征表示外,相似性(或距离)度量也是一项重要的工作,其度量质量直接影响着后期数据挖掘技术的性能和挖掘质量。例如,多元时间序列的聚类、分类、相似性查找和匹配、异常检测等都需要进行距离度量。在时间序列数据挖掘中,最常用的2种方法是欧氏距离(Euclidean distance)[12]和动态时间弯曲方法(dynamic time warping,DTW)[13]。前者能较快地计算序列之间的相似性,适用于等长时间序列的相似性度量;后者对不等长时间序列的距离度量具有较强的鲁棒性,但需要二阶的时间和空间复杂度,不利用大量较长时间序列的相似性度量。针对主成分分析方法得到的特征数据,存在许多距离度量方法来实现特征数据的相似性计算。其中,较为常用的是一种被称为Eros的距离度量方法[14],它利用夹角公式来度量2个特征向量之间的关系,同时以相应的方差作为权重,较好地描述了多元时间序列经过特征变换后特征数据之间的差异性。然而,Eros是根据特征序列方差大小来选择相应特征向量进行匹配,迫使较大方差对应的特征向量被用来计算相似性。另外,权重是由方差的大小决定,使得Eros因过分强调方差的重要性而忽视了特征空间之间的差异性。
针对上述问题,本文提出一种基于特征矩阵的多元时间序列最小距离度量方法,它利用主成分分析对多元时间序列进行特征表示,并获得相应的特征矩阵并构建相应的正交坐标系。另外,通过夹角公式来度量2个多元时间序列对应正交坐标系中不同坐标轴之间的距离,并结合匈牙利算法计算它们之间的最小距离。该方法不依赖于方差的大小来选择夹角向量,而是通过度量正交坐标系之间的相似性来反映原始多元时间序列的差异,进而克服了传统Eros方法的局限性。
1 主成分分析与Eros距离度量主成分分析(PCA)是一种最常用的线性降维方法,是基于某种类型的投影机制,将高维的数据向低维空间(特征空间)投影,并期望在特征空间中数据的方差最大。通过选择占有绝大部分信息的主成分来实现数据降维,同时进行特征表示。换句话说,如果把所有的点映射在一起,则几乎所有的原始信息都将丢失;若映射后数据的方差尽可能大,则数据点将被分开,使得距离信息保留得更多。因此,传统的主成分分析方法通过方差的大小来选择主成分。
对于多元时间序列X=[X1 X2 … Xm]可以表示成一个n×m的矩阵,即X=(xij)n×m。其中,Xj表示第j个变量属性所形成的序列,xij表示多元时间序列第i个时间点第j个变量的观测值,n和m分别表示多元时间序列的时间维度(长度)和变量维度。
根据主成分分析原理,首先需要计算多元时间序列变量之间的协方差,得到一个协方差矩阵Sm×m,再通过奇异值分解对协方差矩阵Sm×m进行特征值和特征向量分解,得到以特征值大小排列形成特征值对角矩阵Σm×m=diag(λ1,λ2,…,λm)和对应的特征矩阵Um×m=[u1 u2 … um],故有

利用主成分分析方法对多元时间序列Xn×m进行特征分解,可以得到相应的特征值和特征矩阵。同时,根据特征值(即方差)的大小,可以选择对应的特征向量作为特征空间中的坐标轴,进而得到相应的主成分。选取前k(k<m)个主成分作为该多元时间序列的特征,即
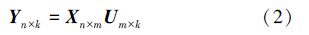
与原始多元时间序列Xn×m相比,由于k<m,特征序列Yn×k实现了数据降维.同时,其对原始数据信息的保存量为e=∑i=1kλi/∑j=1mλj。然而,特征序列Yn×k虽然对多元时间序列进行了降维处理,但仅局限于从变量属性维度进行数据压缩,没有实现从时间属性维度方向的数据降维。鉴于此,部分学者通过比较数据降维后的特征空间来区分原始多元时间序列的数据分布特征[14]。
Eros距离度量方法就是一种基于特征空间的多元时间序列相似性度量方法[14]。它利用主成分分析方法对多元时间序列进行特征分解,得到相应的特征值和特征矩阵。同时,根据特征值的大小,选取对应的特征向量形成特征空间坐标系,并且结合综合权重W来计算2个多元时间序列A和B对应特征空间坐标系之间的相似性,即
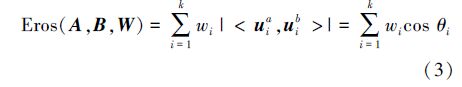
Eros距离度量方法是一种基于特征空间坐标系的相似性度量方法,让2个多元时间序列经PCA转换后前k个坐标轴根据它们的特征值大小进行相应的夹角度量,即一个多元时间序列第i个特征向量与另一个多元时间序列的第i个特征向量进行夹角度量。然而,在某些情况下,一个多元时间序列的第i个特征向量可能与另一个多元时间序列的第j个特征向量的夹角更相似。鉴于此种情况,提出基于特征矩阵的多元时间序列最小距离度量方法。
最小距离度量方法的主要思想就是利用主成分分析方法对数据库中的每个多元时间序列进行特征分解,得到相应的特征向量。通过夹角公式分别计算2个多元时间序列对应前k个特征向量中任意2个向量之间的相似性,并建立夹角距离矩阵。最后通过匈牙利算法[15]对该距离矩阵实现最小距离度量。由于该方法是基于传统Eros的多元时间序列距离度量方法,故亦可称之为MEros (minimum Eros)。
假设2个多元时间序列An1×m和Bn2×m,通过主成分分析方法得到相应的特征矩阵为Ua和Ub,且Ua=[u1a u2a … uma]和Ub=[u1b u2b … umb],则利用夹角公式来计算由特征矩阵Ua和Ub中向量所形成的坐标系中前k个坐标轴之间的相似性,即
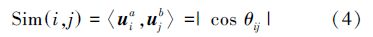

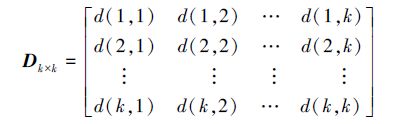
最小距离度量方法就是基于夹角距离矩阵D,根据传统Eros思想找到一组最优匹配,使得该匹配具有最小的距离。即通过PCA降维后,一个多元时间序列的前k个特征向量能够与另一个多元时间序列的前k个特征向量对应比较,并取得最小距离度量。因此,该思路可以归纳为一个线性规划问题:
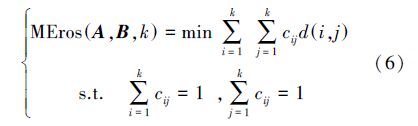
上述线性规划问题实质是一个线性任务分配问题,即k个人分配k项任务,一个人只能分配一项任务,一项任务只能分配给一个人。为此,选取匈牙利算法[15]来解决该线性任务分配问题,该算法是用来解决二分图最小匹配问题的经典算法。对于多元时间序列的主成分之间的最小夹角距离可以从矩阵D出发,把该矩阵的各行和各列分别视为线性任务分配问题中的人员和任务,即如何从距离矩阵D中把第j列的任务分配给第i行的对象,使得最终每个人完成一项任务,且所有人员完成所有任务后花费的代价要求最小。
由于多元时间序列经过主成分分析方法进行变换后,不同多元时间序列的特征向量可以构成不同的坐标系,不同坐标系的维表示的意义各不相同。若简单按照各特征值大小顺序来构建坐标系,并且比较对应坐标系之间的夹角来描述多元时间序列特征的差异性,将显得不合理。针对此问题,利用匹配不同时间序列的特征向量构建的坐标系之间的最小距离,便可以使得2个坐标系中最相似的维被相互比较,进而更为灵活有效地对多元时间序列的特征进行距离度量。
综上所述,基于特征矩阵的多元时间序列最小距离度量算法如下。
算法:最小距离度量dmin=MEros(A,B,k)。
输入:多元时间序列A与B,降维后的维度k。
输出:最小距离度量dmin。
步骤:
1)对多元时间序列A与B计算协方差矩阵,即SA=E[(A-E[A])(A-E[A])T]和SB=E[(B-E[B])(B-E[B])T];
2)利用奇异值分解方法对协方差矩阵进行特征分解,使得SA=UAΣAUAT和SB=UAΣBUBT,其中UA和UB分别为2个协方差矩阵的特征矩阵,且向量按特征值大小排列;
3)分别在UA和UB中选取前k个特征向量作为新坐标系的坐标轴,根据距离度量式(5),建立夹角距离矩阵D;
4)利用匈牙利算法对夹角距离矩阵进行最小距离计算,即dmin=munkres(D),其中,munkres为匈牙利算法求解二分图最小匹配问题的函数。
基于特征矩阵的多元时间序列最小距离度量方法能够有效地描述原始多元时间序列之间的相似性。同时,与传统Eros方法相比,最小距离度量方法MEros不受其他多元时间序列经PCA转化后特征值的影响。通过比较特征向量所形成的坐标系之间的差异性来区分不同多元时间序列的特征,不仅能够有效地对多元时间序列进行特征描述,而且还能从时间维度和变量维度2个方向进行数据降维,即原来n×m维降至k×k维.通常情况下,k<n和k<m。
需要说明的是,最小距离度量方法利用匈牙利算法对夹角距离矩阵进行最优化匹配求解,最坏情况下,其消耗的时间复杂度为O(k3)。然而,在大多数情况下,经过PCA转化后,较小的k值所对应的主成分也能保留原始多元时间序列的大部分信息,使得最小距离度量能够快速有效地对多元时间序列进行相似性度量。
3 数值实验为了有效地评估MEros方法的性能,利用多元时间序列聚类和分类算法进行距离度量质量检测,同时比较了几种方法的计算时间效率。
3.1 数据聚类层次聚类方法能够较好地从视觉角度表达聚类结果的层次关系,并且能够很好地评估数据距离度量方法的准确性。本次实验能过层次聚类算法和3种距离度量方法(MEros、Eros和欧氏距离Euclidean)来对等长多元时间序列进行聚类分析,进而比较3种距离度量方法的度量质量.
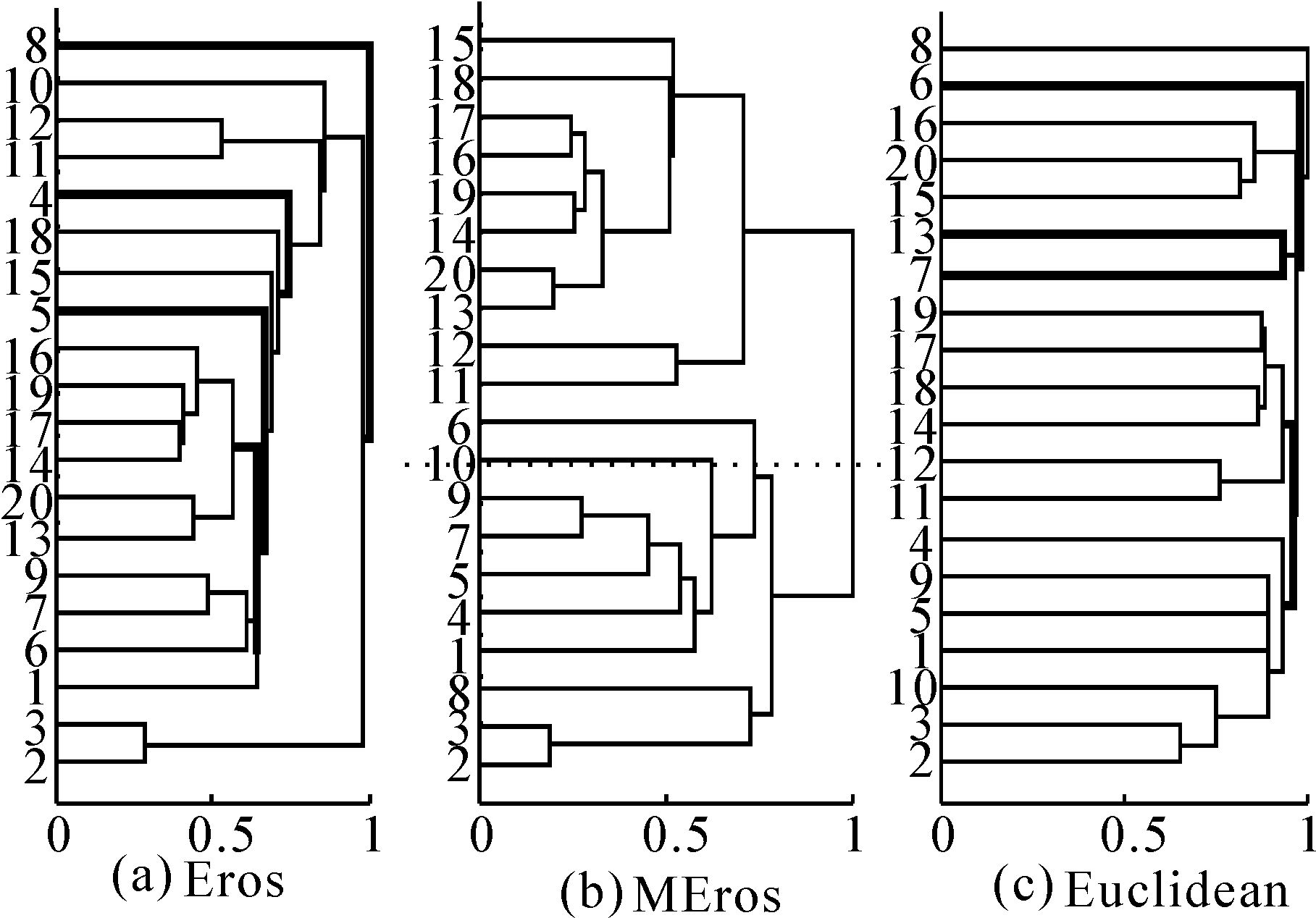
实验数据为EEG多元时间序列数据集,它具有2类标签且包含了20个多元时间序列,每个时间序列具有相同的观测时间,即时间序列长度相同且为256,是对64个部位进行观测的序列数据,可视为256×64的数据矩阵。同时,前后10个多元时间序列分别为同一类数据,即序号为{1,2,3,4,5,6,7,8,9,10}为同一类,其余{11,12,13,14,15,16,17,18,19,20}为另外一类。在本次实验中,选取k=3为主成分分析降维后的维度,并将相应的特征数据用于考查MEros和Eros的度量性能,其聚类分析结果如图 1所示。从层次聚类结果视图中分析易知,距离度量方法Eros和欧氏距离Euclidean对等长多元时间序列数据的聚类出现明显的错误归类,如图 1(a)和图 1(c)中粗连线所示,它们将不同类的数据对象错误地归为一类。然而,本文提出的距离度量方法MEros能够很好地将2类数据成功归类,如图 1(b)所示,前后10个数据对象分别被归成一类,符合实际分类情况。因此,可以说MEros具有较好的距离度量质量,能够提高多元时间序列数据的聚类性能。
|
| 图 1 3种度量方法对等长多元时间序列的聚类结果 Fig. 1 The clustering results of the tree measurements for multivariate time series with different lengths |
聚类分析实验采用等长多元时间序列EEG数据集和另外一个不等长多元时间序列EEGEye数据集[16],它们都是具有2类标签的多元时间序列数据集。同时,EEGEye数据集中包含24个长度不等的多元时间序列,其长度范围21~2 051,具有14个观测属性。
利用最近邻分类方法比较MEros、Eros和欧氏距离Euclidean或动态时间弯曲DTW等方法在多元时间序列数据集的度量效果,通过分类错误率来评价距离度量方法的质量。让多元时间序列数据集中的每个序列都与其他序列进行距离度量,查找与之最相似的序列作为检测序列,并通过比较检测序列与被检测序列之间的标签来判断分类结果的正确性,最终通过平均分类错误率来衡量距离度量方法在分类实验中的应用性能。
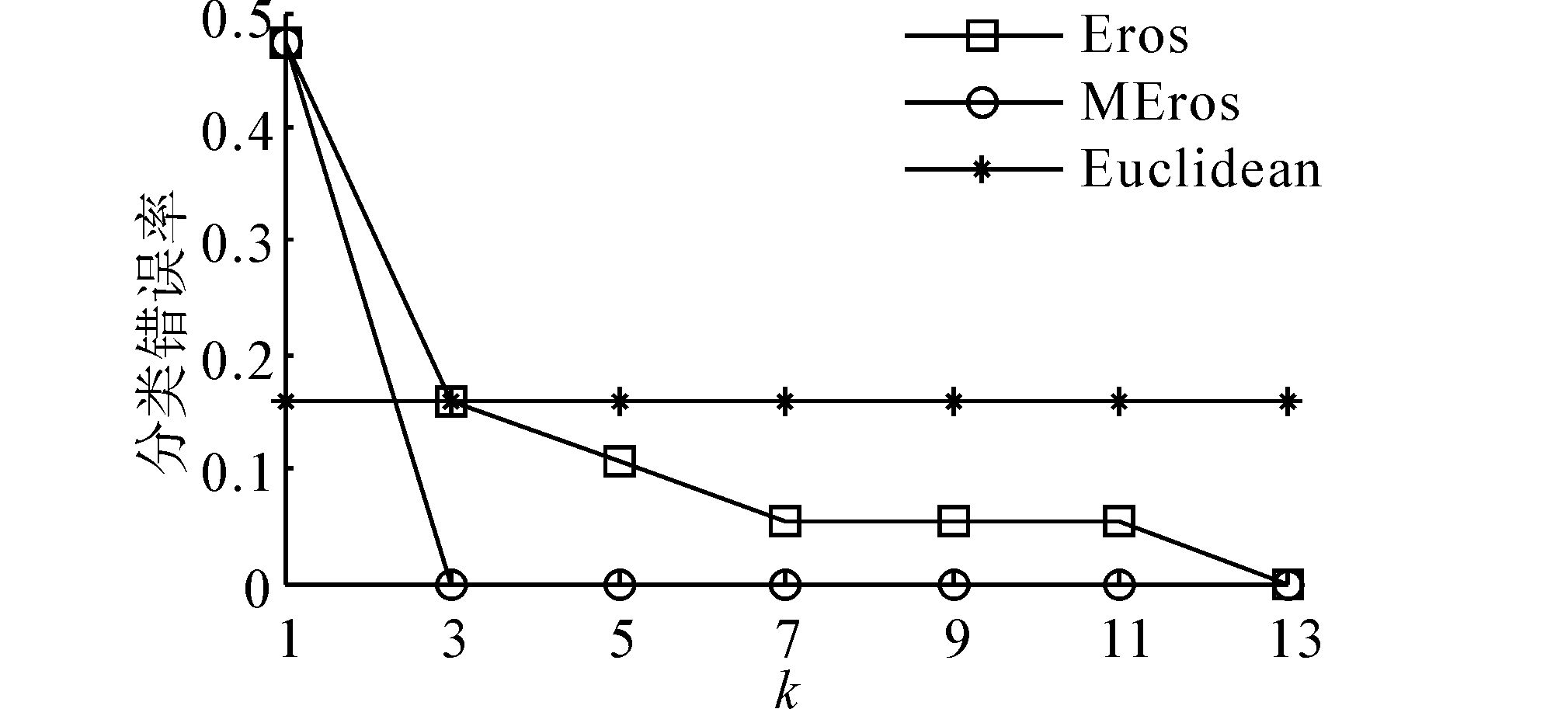
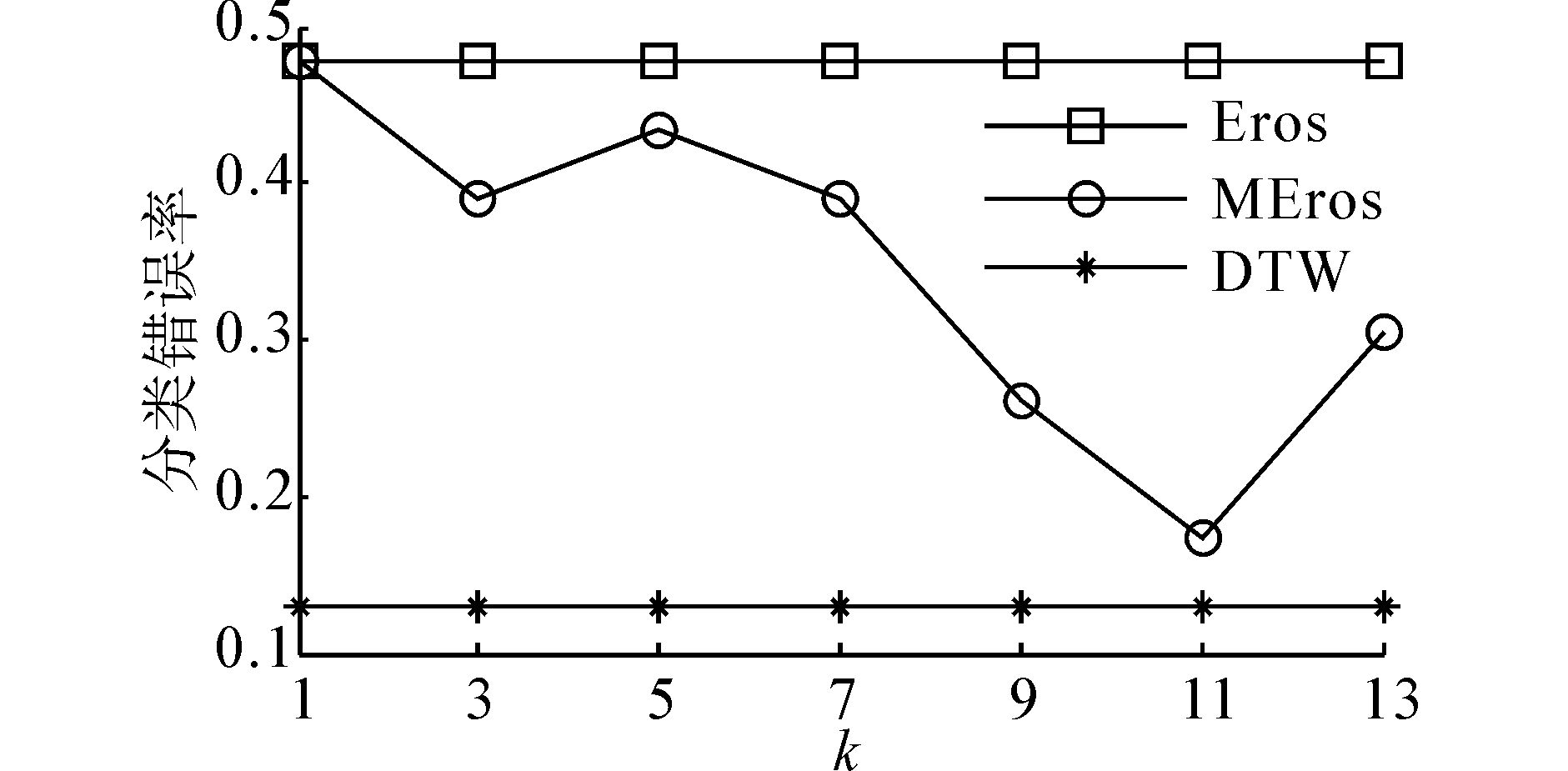
另外,选取不同的降维维度来比较距离度量方法在分类实验中的性能,即通过比较不同维度k的坐标系来考察距离度量的质量。对等长时间序列数据集EEG和不等长时间序列数据集EEGEye的分类结果如图 2和3所示。从分类实验结果可以发现,与传统方法Eros相比,新方法MEros具有较好的分类结果,说明它具有更好地距离度量质量,能够提高多元时间序列数据挖掘的挖掘效果。另外,由于Euclidean和DTW分别善于对等长和不等长时间序列的相似性度量,故在实验中比较它们与新方法的分类效果。在图 2分类结果中发现,MEros具有最好的分类结果,而在图 3分类结果中可以知道,在对不等时间序列相似性比较时,DTW的分类质量优于MEros,其原因是EEGEye数据集的形态特征区分较为明显,利用DTW通过最优化路径选择并产生相应的距离值,它能够使其取得较好的分类效果,但从时间效率比较实验中易知,DTW时间消耗不适合于大量高维时间序列的数据挖掘。
|
| 图 2 3种方法对EEG数据集的分类结果 Fig. 2 The classification results of three methods for EEG |
|
| 图 3 3种方法对EEGEye数据集的分类结果 Fig. 3 The classification results of three methods for EEGEye |
为了更好地比较距离度量方法之间的性能,除了评价它们在多元时间序列数据挖掘中的挖掘质量,还需要评估其实际实验中的运行效率。根据上面实验步骤,记录每个检测序列与被检测序列之间相互匹配的CPU计算时间,将平均消耗时间作为最终的评估时间代价。另外,根据不同的k值,观测距离度量方法的时间消耗情况。
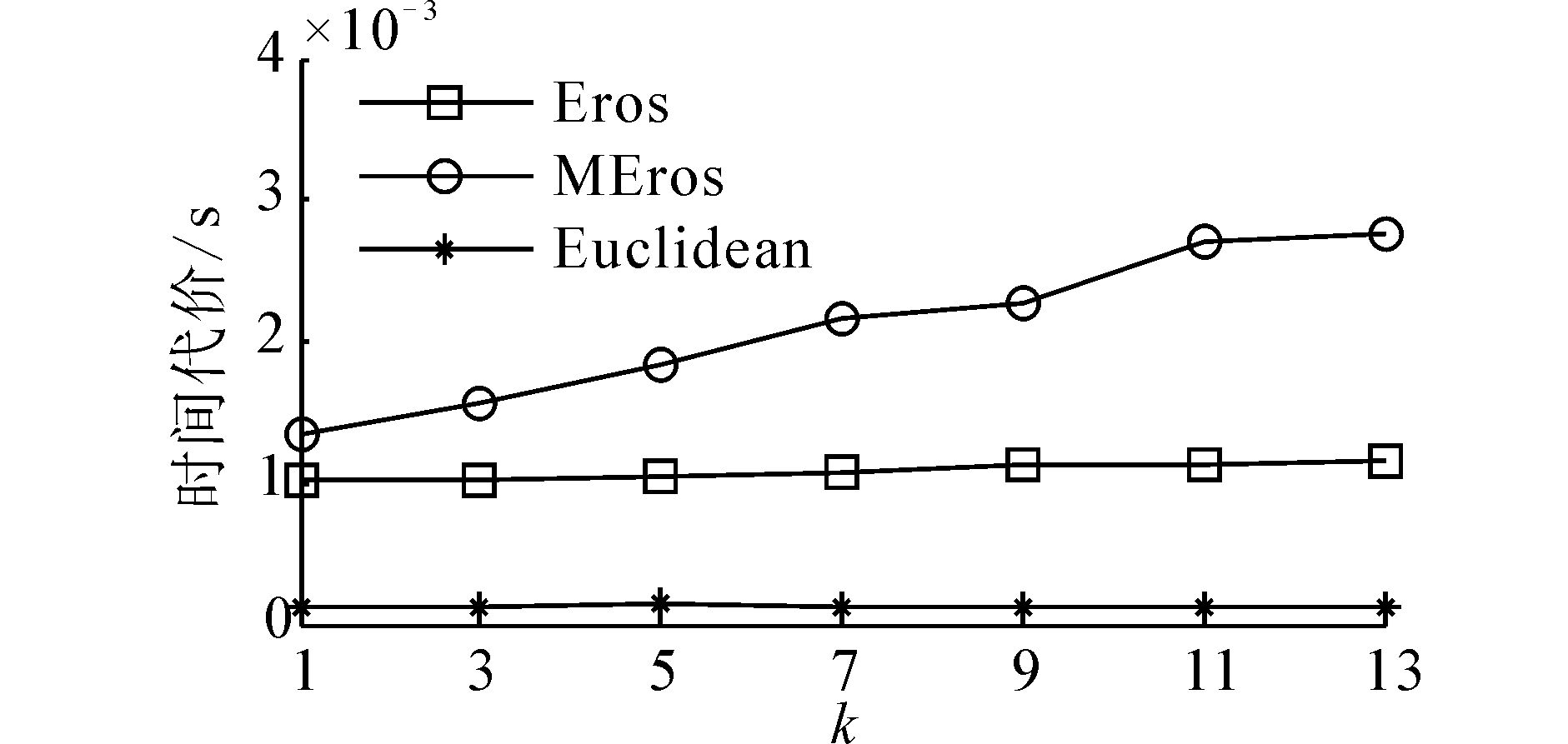
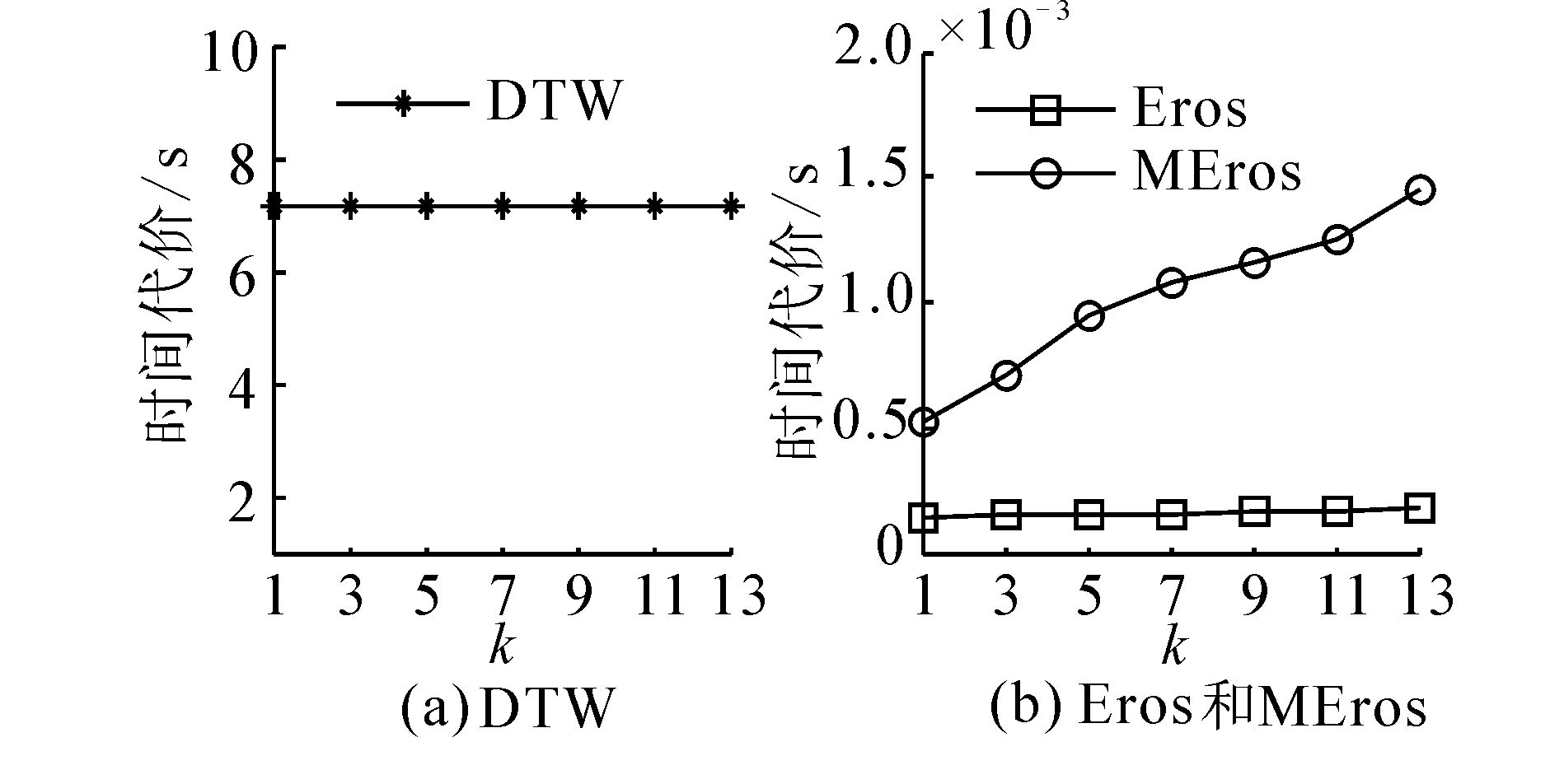
3种距离度量方法对2组时间序列数据集的CPU时间代价如图 4和图 5所示。容易发现,与Euclidean和Eros相比,新方法MEros需要消耗较多的计算时间。然而,从实验结果中的纵轴数据量大小易知,这3种方法仅需要10-3秒级的时间。然而,对于不等长时间序列度量来说,DTW需要平均消耗7.2 s左右的时间。相比之下,适合计算不等长时间序列之间距离的其他2种方法(Eros和MEros)的计算效率明显较好。另外,如图 4和图 5(b)所示,MEros的计算时间随着降维后维度k值的增长而变大,其原因是MEros算法过程中的匈牙利方法计算速度依赖于k值,即O(k3)。k值越大,其计算时间代价越高,但其运算速度保持在10-3秒级。因此,结合前面的分类实验结果,可以说明新方法MEros是一种较为快速且更为有效的多元时间序列相似性度量方法。
|
| 图 4 3种方法对EEG数据集的时间代价 Fig. 4 he time cost of the three methods for EEG |
|
| 图 5 3种方法对EEGEye数据集的时间代价 Fig. 5 The time cost of the three methods for EEGEye |
文章提出了一种基于特征矩阵的多元时间序列最小距离度量方法。该方法是基于主成分分析特征表示的距离度量方法,首先利用主成分分析对多元时间序列进行特征分解,根据特征值的大小选择相应的特征向量构建反映多元时间序列数据特征的坐标系,并且通过比较坐标系之间的差异性来度量多元时间序列之间的距离。该方法不依赖于特征值(方差)的大小来选择夹角向量,而是通过度量正交坐标系之间的相似性来反映原始多元时间序列的差异,进而克服了传统Eros方法的局限性。同时,通过匈牙利算法,把线性规划问题转化为求解二分图最小匹配问题,其计算原理简单明了。最后,数值实验结果表明,新方法MEros是一种快速有效的多元时间序列距离度量方法。
与传统Eros相比,新方法MEros具有较高的度量质量,但其时间效率略低。MEors算法主要包括了多元时间序列的协方差矩阵、特征矩阵、距离矩阵和匈牙利算法等计算过程,其中前3个矩阵在传统Eros算法中都需要被运算,因此MEros的额外计算时间代价主要是由匈牙利算法求解二分图最小匹配问题引起的。另外,匈牙利算法对距离矩阵的求解效率依赖于多元时间序列的降维后维度k,其最坏情况下的计算时间效率为O(k3)。因此,如何提升匈牙利算法的计算时间或研究一种能够快速求解式(6)的算法是将来有待研究的问题。
| [1] | ESLING P, AGON C. Time-series data mining[J]. ACM Computing Surverys, 2012, 45(1): 11-12. |
| [2] | 李海林, 杨丽彬. 时间序列数据降维及特征表示新方法[J]. 控制与决策, 2013, 28(11):1718-1722.LI Hailin, YANG Libin. Novel method of dimensionality reduction and feature representation for time series[J]. Control and Decision, 2013, 28(11):1718-1722. |
| [3] | YANG K, SHAHABI C. An efficient k nearest neighbor search for multivariate time series[J]. Information and Computation, 2007, 205(1): 65-98. |
| [4] | 韩敏, 李德才. 基于EOF-SVD模型的多元时间序列相关性研究及预测[J]. 系统仿真学报, 2008, 20(7): 1669-1672HAN Min, LI Decai. Multiple time series correlation extraction and prediction based on EOF-SVD model[J]. Journal of System Simulation, 2008, 20(7): 1669-1672. |
| [5] | WENG Xiaoqing, SHEN Junyi. Classification of multivariate time series using two dimensional singular value decomposition[J]. Knowledge-Based Systems. 2008, 21(7): 535-539. |
| [6] | 吴虎胜, 张凤鸣, 钟斌. 基于二维奇异值分解的多元时间序列相似匹配方法[J]. 电子与信息学报, 2014, 36(4): 847-854.WU Husheng, ZHANG Fengming, ZHONG Bin. Similar pattern matching method for multivariate time series based on two-dimensional singular value decomposition[J]. Journal of Electronics & Information Technology, 2014, 36(4): 847-854. |
| [7] | 樊继聪, 王友清, 秦泗钊. 联合指标独立成分分析在多变量过程故障诊断中的应用[J]. 自动化学报, 2013, 39(5): 494-501.FAN Jicong, WANG Youqing, QIN Sizhao. Combined indices for ICA and their applications to multivariate process fault diagnosis[J]. Acta Automatica Sinica, 2013, 39(5): 494-501. |
| [8] | 梁胜杰, 张志华, 崔立林, 等. 基于主成分分析与核独立成分分析的降维方法[J]. 系统工程与电子技术, 2011, 33(9): 2144-2148. LIANG Shengjie, ZHANG Zhihua, CUI Lilin, et al. Dimensionality reduction method based on PCA and KICA[J]. Systems Engineering and Electronics, 2011, 33(9): 2144-2148. |
| [9] | 李正欣, 郭建胜, 惠晓滨, 等. 基于共同主成分的多元时间序列降维方法[J]. 控制与决策, 2013, 28(4): 531-536.LI Zhengxin, GUO Jiansheng, HUI Xiaobin, et al. Dimension reduction method for multivariate time series based on common principal component[J]. Control and Decision, 2013, 28(4): 531-536. |
| [10] | 李正欣, 张凤鸣, 张晓丰, 等. 多元时间序列特征降维方法研究[J]. 小型微型计算机系统, 2013, 34(2): 338-346.LI Zhengxin, ZHANG Fengming, ZHANG Xiaofeng. Research on feature dimension reduction method for multivariate time series[J]. Journal of Chinese Computer Systems, 2013, 34(2): 338-346. |
| [11] | LI Hailin. Asynchronism-based principal component analysis for time series data mining[J]. Expert Systems with Applications, 2014, 41(6): 2842-2850. |
| [12] | YANKOV D, KEOGH E, REBBAPRAGADA U. Disk aware discord discovery: finding unusual time series in terabyte sized datasets[J]. Knowledge and Information Systems, 2007, 17(2): 381-390. |
| [13] | CHEN Yanping, HU Bing, KEOGH E, et al. DTW-D: time series semi-supervised learning from a single example[C]//Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Chicago, USA, 2013: 383-391. |
| [14] | YANG K, SHAHABI C. A PCA-based similarity measure for multivariate time series[C]//Proceedings of the 2nd ACM International Workshop on Multimedia Databases. Washington, DC, USA, 2004: 65-74. |
| [15] | 何坚勇. 运筹学基础[M]. 北京: 清华大学出版社, 2006: 217-220. |
| [16] | BACHE K, LICHMAN M. UCI machine learning repository. (2013-12-21)[2014-4-28]. http://archive.ics.uci.edu/ml. |



