基于视觉的人体动作姿态估计和识别在高级人机交互、智能视频监控、三维动画合成、电影特技制作、体育运动分析、医学理疗等多个方面拥有十分广阔的应用前景,正逐渐受到越来越多学者们的关注。人体动作姿态分析主要分为2个部分:人体姿态描述和人体姿态识别。人体动作姿态识别算法是否有效通常取决于使用的动作姿态表示特征量,因而针对特定问题提出行之有效的动作姿态表示方法成为动作姿态识别研究的重要内容之一。D. Weinland等[1]提出用MHV(motion history volumes)模板描述动作姿态;Wang在2006年提出用轮廓的平均运动形状和运动前景的平均运动能2个模板,用最近邻分类器描述动作姿态[2]。传统的基于视觉的人体动作姿态检测主要针对二维特征,随着运动捕获技术的成熟和推广,高效、快捷获取大量三维的运动数据集已经成为现实。R. Girshick等[3]利用Kinect深度图像分析人体姿态变化。S. Sempena等[4]在2011年利用从Kinect深度图像中得到的人体骨骼模型,采用关节角描述人体动作姿态。结果表明,相对于二维特征,基于Kinect传感器的三维运动捕获数据较好地保持了运动细节,并真实地记录了运动轨迹,数据精度高,并且相比于人体深度数据,采用骨骼数据能够更加紧凑和鲜明地反应人体姿态。对于人体动作姿态识别,常用的方法有动态时间规整(dynamic time warping,DTW)、动态贝叶斯(dynamic Bayesian,DBN)、隐马尔科夫模型(hidden Markov models,HMM)、神经网络等。如A. Veeraraghavan等[5]使用DTW方法匹配动作序列,Luo[6]采用动态贝叶斯网络进行人体动作姿态识别研究,并与HMM方法进行了比较,F. Buccolieri[7]通过径向基神经网络(radial-basis function,RBF)分析人体轮廓特征来识别姿态。
相比上述方法,基于支持向量机的学习算法利用结构风险最小化代替传统模式识别中的经验风险最小化,对解决高维数、非线性和小样本的问题很有优势。鉴于此,本文提出了一种多类支持向量机人体动作姿态识别方法。该方法运用Kinect骨骼追踪技术提取人体骨骼模型,并针对人体关节的特点在关节点处建立球坐标系,利用关节角对人体动作姿态进行描述。同时,利用高斯核模型设计了基于测地线距离的姿态核函数,采用二叉树设计多类支持向量机算法对人体姿态进行识别。
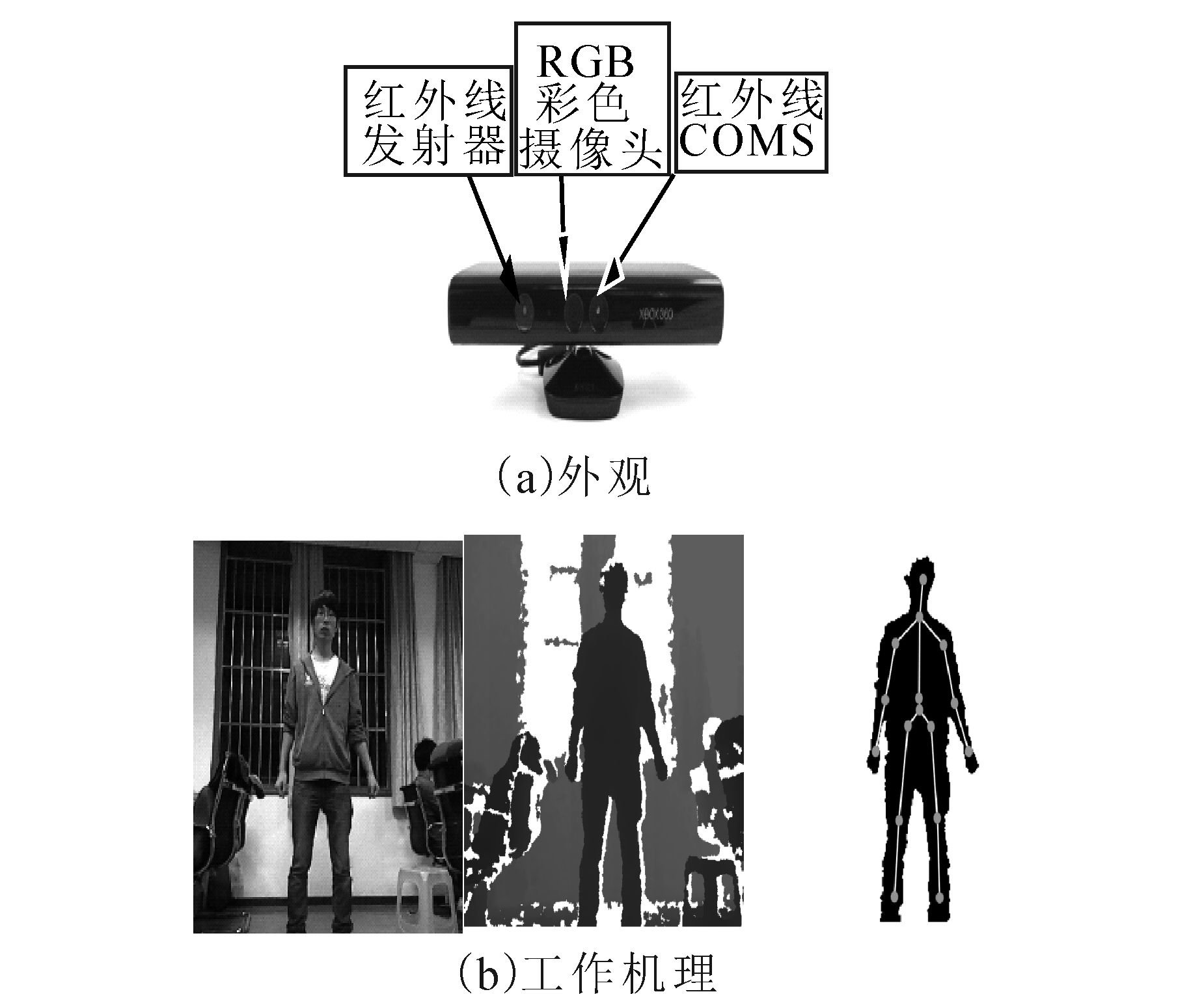
1 人体姿态表示 1.1 Kinect简介Kinect传感器是微软公司开发的一种3D体感摄像机,它由1个红外投影仪、2个摄像头组成,如图 1(a)所示。Kinect工作原理的核心是通过类似结构光法的光编码(light coding)技术的方式来获取深度图像。红外发射器连续地向空间发射光,并给空间编码,通过普通CMOS合成黑白深度图像,其中纯黑代表无穷远,纯白代表无穷近。由于不需要特制的感光芯片,极大地降低了成本,越来越多的学者采用它进行深度图像的采集。本文利用分割技术将人体从深度图像背景环境中区分出来,并采用随机森林[8]等分类算法将人体各个部位进行区分定位,得出骨骼关节点的坐标信息。每一帧的骨骼图像中都有被跟踪人的姿势,包括20个关节点,并以30帧/s的速度生成骨骼图像流,实时地重现人体的运动状态,骨骼提取流程如图 1(b)所示。
|
| 图 1 当Kinect外观和工作机理 Fig. 1 The appearance of the Kinect and the mechanism |
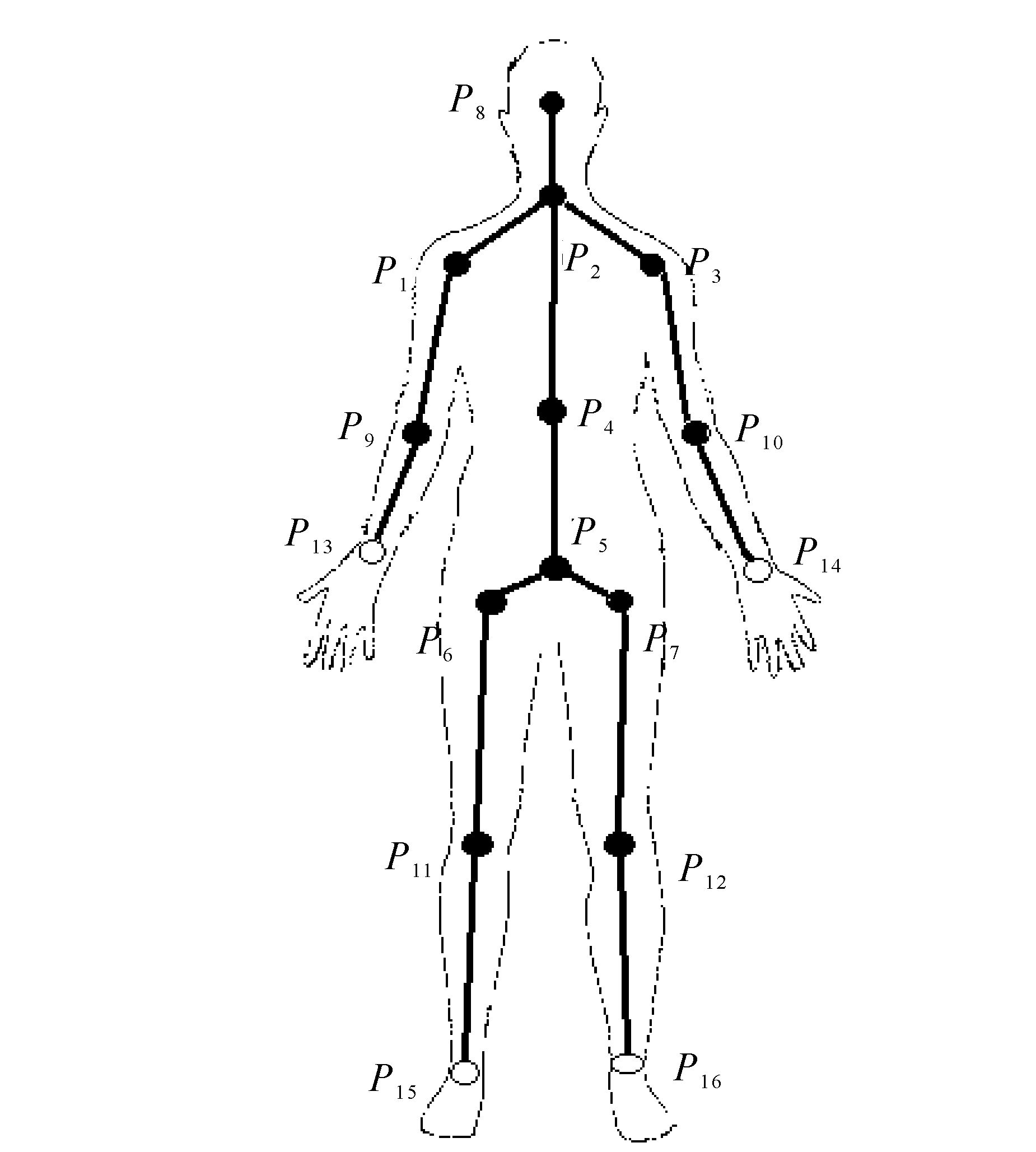
Kinect传感器获取的景深图像中可以提取出人体20个关键点的位置信息,本文选取其中的16个骨骼点构成人体的骨架模型,每一个关节点的位置用Kinect坐标系下的三维向量表示Pi=(xi,yi,zi)T,其中xi,yi代表在彩色图像上位置,zi表示关节点离传感器的距离。如图 2所示,16个骨骼点中P1,P2,…,P7分别为人体的右侧肩、颈部、左侧肩、脊柱、髋骨中心、右髋、左髋,共同构成人体的躯干部分;P8为人体头部;P9,P10,…,P16代表人体的四肢部分,包括左右侧肘关节、腕关节、膝关节和踝关节。在绘制骨架图时,保证了骨架的大小不会因人到传感器位置或者身体的整体平移而发生改变,以达到更好的人机交互效果。
|
| 图 2 人体骨架框图 Fig. 2 Human skeleton diagram |
由于人体的动作姿态描述可以用四肢部分和头部相对于躯干部分的位置变化来表示。因此,将构成骨架框图的16个关节点分为3个部分:第1部分是构成人体躯干的关节点,包括P1,P2,…,P7;第2部分是所有与人体躯干相邻的关节点,包括P8,P9,…,P12;第3部分是与第2部分关节点相邻的关节点,包括P13,P14,P15,P16。这样,通过第2、3部分的9个关节点相对于第1部分人体躯干的各个关节角度变化就可以描述人体动作姿态。
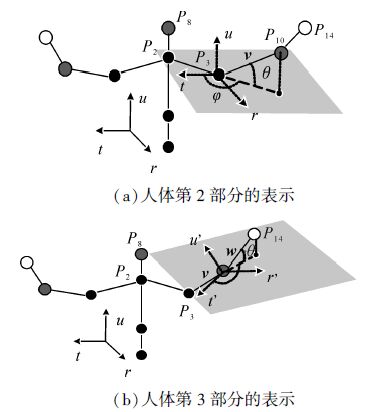
运用PCA主成分析法将第1部分的人体躯干7个关节点用1个三维向量表示,并将三维向量进行施密特正交化处理,用{u,r,t}表示(如图 3),其中u表示人体的上下运动,r表示人体的前后运动,t表示人体的左右运动,显然t=u×r。人体的关节是球形关节,其余2部分的运动以此为基准,分别在与上级部分连接的关节点处建立一个球面坐标系。以描述左手臂的运动为例,第2部分从左肩到左肘的向量v,第3部分从左肘到左腕的向量w。第2部分的坐标系以{u,r,t}为基准,原点在P3;第3部分的坐标系是将{u,r,t}以轴心b=v×r旋转α=cos-1(v·r)角度得到,记作{u′,r′,t′},原点在P10。给定一个体,由于人体骨骼长度不变性,根据球面坐标系的定义,关节点的运动可用仰角θ和方位角φ加以约束。其中θ为v与平面tP3r的夹角以及w在平面t′P10r′的夹角,即仰角;φ为t轴和v在平面tP3r上投影的夹角以及t′轴与w在平面t′P10r′上投影的夹角,即方位角。所以用(θ1,φ1),(θ2,φ2)可分别表示P10、P14点的运动,其他关节点计算类似。综上,第2、3部分共有9个关节点,可用一个18维的特征向量:
υ=[θ1φ1θ2φ2…θ9φ9]∈R18
来表示人体动作姿态每一帧姿势,其中每一对(θi,φi)都表示其对应关节点在相应坐标系下的位置。如图 3所示。
|
| 图 3 人体行为描述 Fig. 3 Description of human behavior |
支持向量机(support vector machine,SVM)方法是在统计学习理论基础上发展起来的一种有监督的分类和回归方法。其核心思想是在一个n维空间中构造一个超平面用来区分特征空间中的类模式,且模式之间的距离最大。为计算2类模式的距离,在分类面的2侧构建2个平行于分类面的超平面,在这2个超平面上的数据称为支持向量。
支持向量机分类算法的数学描述如下:假定对于给定的一组训练集为T={(υ1,c1),(υ2,c2),…},υi为姿态特征向量υi∈R18,yni∈{+1,-1},ci∈{1,2,...,|k|}为姿态类别标签。当样本υi属于第i类ci时,其类别表示yni=+1,否则yni=-1。通过一个非线性映射φ(·),把训练样本映射到一个高维空间中:φ:Rn→H。由于提取的特征是非线性的,支持向量机最优分类面的求解问题则可以表示为
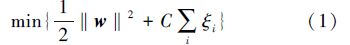
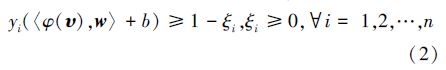
通常求解式(1)时采取其拉格朗日对偶问题的方法:
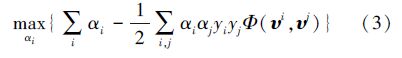
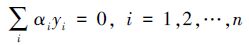 ,,Φ(υi,υj)为核函数。其决策函数fi(υ)描述为
,,Φ(υi,υj)为核函数。其决策函数fi(υ)描述为
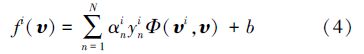
采用核函数的作用是简化映射空间中的内积运算,将非线性的训练数据隐式映射到高维空间,而不增加可调参数的个数。在常用的核函数中,高斯函数因其优越性能引起人们的关注。高斯函数的表达式为
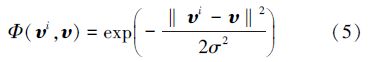
假设给出2个球面上的点υi=(θi,φi),υj=(θj,φj),则这2点间的测地线距离δ(υi,υj)为
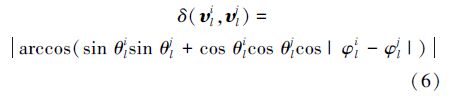
令υi,υj是2个姿态特征向量,对于关节点l,δ(υli,υlj)表示的是该关节点2种姿态描述下构成点对之间的测地线距离。取9个关节点的测地线距离的平方和,记为
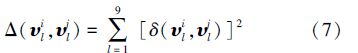
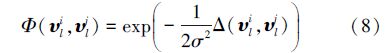
下面证明该核函数是一个有效的核函数。首先给出核函数Γ(υli,υlj)的表达式:
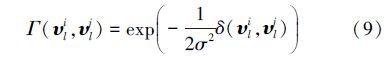
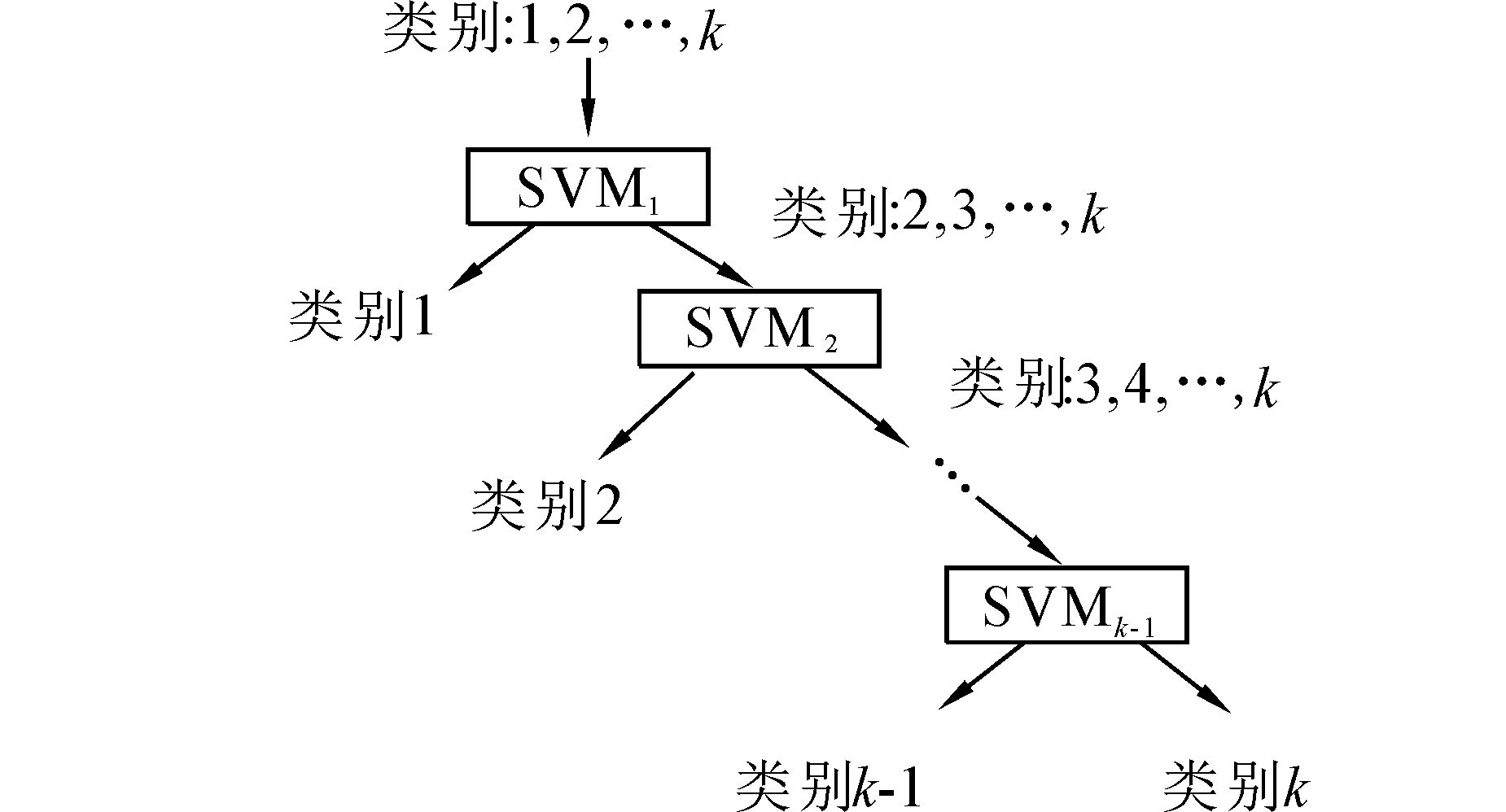
SVM最初仅用于实现2类问题的分类,要实现12种人体姿态的多类分类,需要对标准SVM进行扩展,将多个标准SVM以某种方式组织在一起,构建多类支持向量机。目前构建MSVM的方法主要有一对一、一对多方法、导向无环图和二叉树[12]。鉴于二叉树设计方法的诸多优点,采用决策二叉树的多类分类器设计方法,如图 4所示。
|
| 图 4 二叉树的多类分类器框架 Fig. 4 The multi-class classifier framework of binary tree |
在二叉树结构中,根据决策半径构造二叉树各内节点的最优超平面,即从根节点开始,沿树的路径依次得到的类别标签为1,2,…,k。二叉树各内节点的分类算法流程如下:1)以第1类样本为正样本集,其他类样本为负样本集,构造二值分类器,将1类从样本集中剔除;2)以第2类样本为正样本集,其他类样本为负样本集,构造第2个内节点处的二值分类器,将2类从样本集中剔除;3)依次下去,可以得到基于二叉树的多类支持向量机分类器。
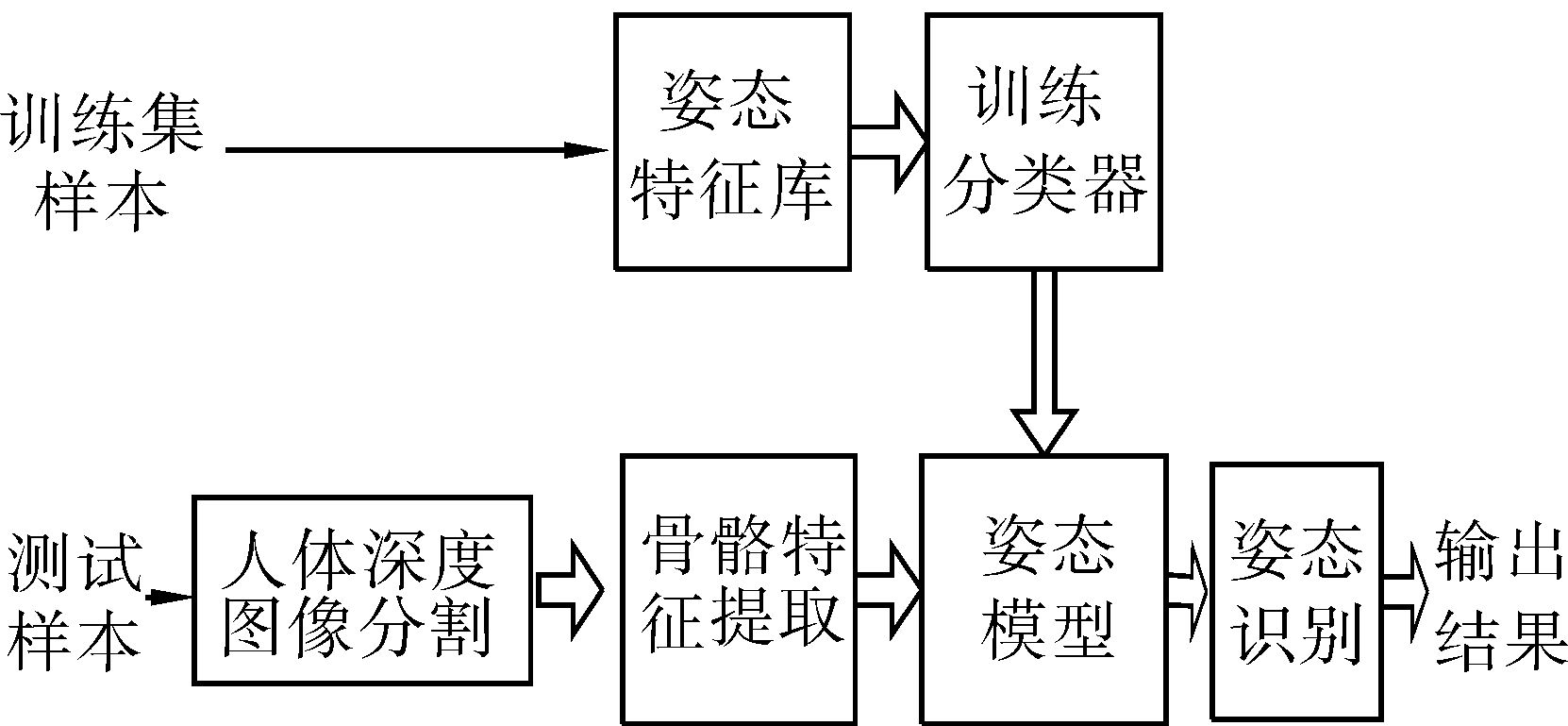
3 实验结果与分析整个实验的环境:Kinect传感器彩色图像分辨率为640×480、深度图像分辨率为320×240;软件开发环境:Window7+Visual Studio 2010、Kinect SDK-v1.7;开发语言:C#。本文提出的人体姿态识别算法可分为4个部分:人体深度图像分割、骨骼特征提取、姿态模型和姿态识别,如图 5所示。
|
| 图 5 姿态识别算法框架 Fig. 5 Human posture recognition algorithm framework |
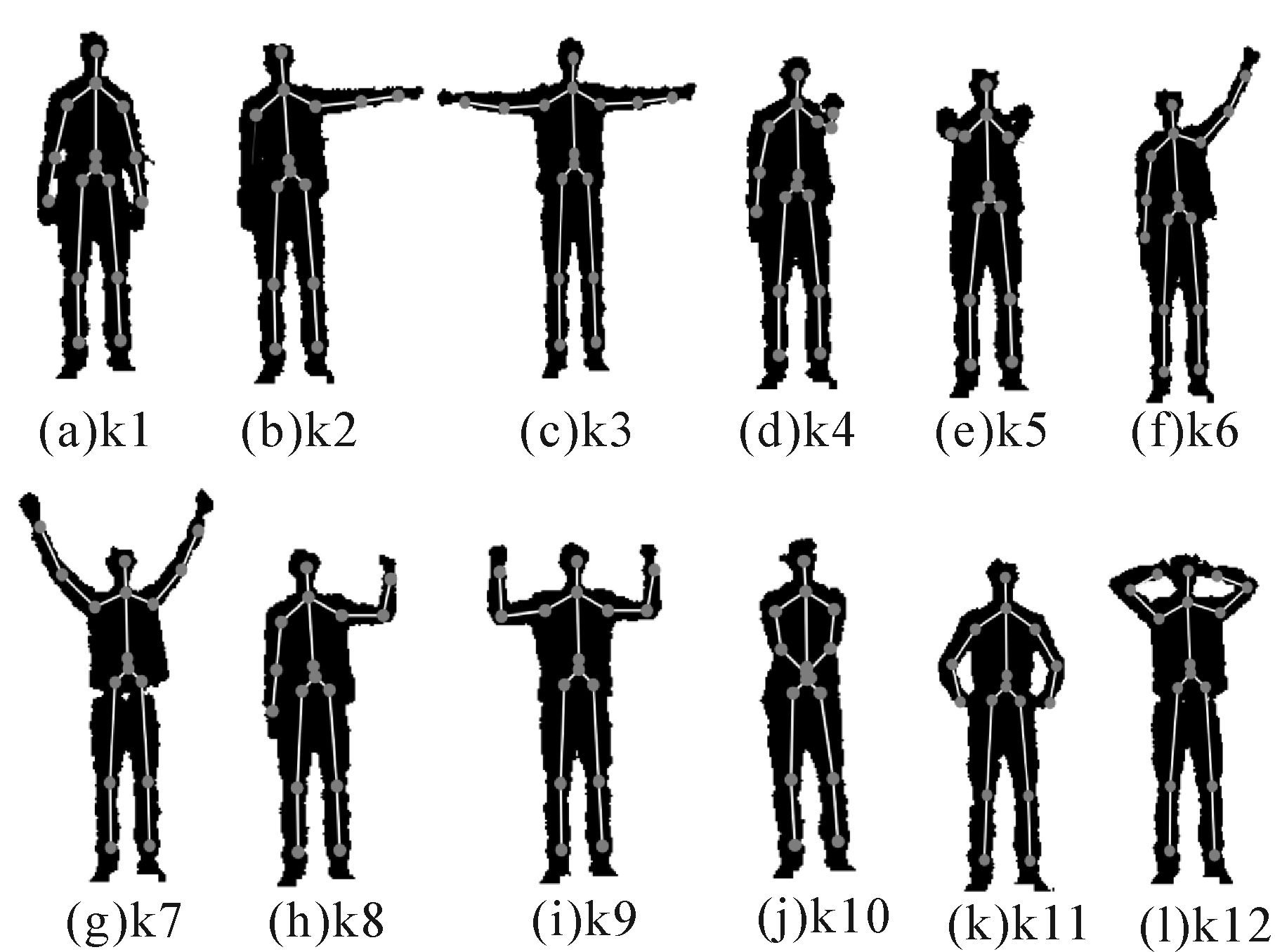
本文主要是研究人体上肢部分的运动姿态,为验证算法的可行性及正确率,选取Kinect Gesture Data Set(the MSR Action3D dataset)数据集中人体上肢部分的12种姿态作为训练姿态进行识别,各个姿势如图 6所示。
|
| 图 6 人体12种上肢姿态 Fig. 6 kinds of human upper limb postures |
在训练样本集时,每一种姿势进行30次训练,创建姿势样本集:K={c1,c2,...,ck}。为验证改进核函数后算法的有效性,分别基于传统欧氏距离的高斯核函数多类支持向量机和采用改进的基于测地线距离的高斯核函数多类支持向量机算法识别这12种姿态,让10位同学对每个姿势进行50次实验,分类结果如表 1所示。
|
姿态 标签 | 基于传统核函数 | 基于改进核函数 | ||
| 正确次数 | 准确率/% | 正确次数 | 准确率/% | |
| k1 | 49 | 98 | 50 | 100 |
| k2 | 46 | 92 | 48 | 96 |
| k3 | 46 | 94 | 49 | 98 |
| k4 | 45 | 90 | 47 | 94 |
| k5 | 44 | 88 | 48 | 96 |
| k6 | 47 | 94 | 48 | 96 |
| k7 | 46 | 92 | 49 | 95 |
| k8 | 47 | 94 | 48 | 96 |
| k9 | 45 | 90 | 48 | 97 |
| k10 | 44 | 88 | 46 | 92 |
| k11 | 47 | 94 | 49 | 98 |
| k12 | 46 | 92 | 48 | 96 |
在实验中发现,当某些姿态比较相似时,例如k7、k9和k12,这些姿态之间有一定的误判,但误判比例较小,整体的分类效果还是比较好的。从表 1中可以得出,提出的改进高斯核函数多类支持向量机算法的平均识别率为96.1%,比传统的基于欧氏距离的高斯核函数多类支持向量机算法提高了3.9%。因此,所采用的分类器在监督学习机制下是有效的分类器模型,验证了系统所提取的特征能有效表示特征姿态。同时,为了验证本算法对姿态的分类和识别具有优越性,利用RBF神经网络对采集的k7、k9和k12 3种误判较高的姿态进行分类,同样让10位同学对每个姿势进行50次实验,将实验结果与本文方法进行比较,见表 2所示。由表 2对比结果可以看出,对于k7、k9和k12这3种姿态的识别,本文方法用时略快于RBF神经网络,且识别率更高,具有较好的小样本分类性能。
|
姿态 标签 | RBF神经网络方法 | 本文方法 | ||
| 用时/s | 识别率/% | 用时/s | 识别率/% | |
| k7 | 0.023 6 | 95 | 0.011 7 | 95 |
| k9 | 0.307 0 | 94 | 0.019 6 | 97 |
| k12 | 0.038 2 | 94 | 0.020 3 | 96 |
在充分研究常用行为表示方法的基础上,针对人体骨骼关节的特点提出了基于球坐标系下人体关节角的行为表示特征量。并针对欧氏距离计算方法难以完全反映人体关节运动数据样本点与测试点之间位置关系的问题,采用测地线距离代替欧氏距离的对高斯核函数进行改进,构建基于测地线距离的姿态核函数。最后,创建了基于二叉树的多类支持向量机对人体12种常见上肢行为姿态进行识别,并通过和其他姿态识别方法对比,验证了该人体姿态识别方法的优越性,具有较高的识别率。然而,本文的人体姿态识别只是针对某种特定姿势,实际生活中,人体的姿势往往是连续的。未来的工作将是把特定姿势作为人体动作的关键姿势,并按照一定的顺序编排成运动序列,完成连续姿态序列的行为识别。
| [1] | WEINLAND D, RONFARD R, BOYER E. Free viewpoint action recognition using motion history volumes[J]. Computer Vision and Image Understanding, 2006, 104(2/3): 249-257. |
| [2] | WANG Liang, SUTER D. Informative shape representations for human action recognition[C]//18th International Conference on Pattern Recognition. Hong Kong, China, 2006, 2: 1266-1269. |
| [3] | GIRSHICK R, SHOTTON J, KOHLI P, et al. Efficient regression of general-activity human poses from depth images[C]//2011 IEEE International Conference on Computer Vision (ICCV). Barcelona, Spain, 2011: 415-422. |
| [4] | SEMPENA S, MAULIDEVI N U, ARYAN P R. Human action recognition using dynamic time warping[C]//2011 International Conference on Electrical Engineering and Informatics (ICEEI). Bandung, Indonesia, 2011: 1-5. |
| [5] | VEERARAGHAVAN A, ROY-CHOWDHURY A K, CHELLAPPA R. Matching shape sequences in video with applications in human movement analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(12): 1896-1909. |
| [6] | LUO Ying, WU T D, HWANG J N. Object-based analysis and interpretation of human motion in sports video sequences by dynamic Bayesian networks[J]. Computer Vision and Image Understanding, 2003, 92(2/3): 196-216. |
| [7] | BUCCOLIERI F, DISTANTE C, LEONE A. Human posture recognition using active contours and radial basis function neural network[C]//IEEE Conference on Advanced Video and Signal Based Surveillance. Como, Italy, 2005: 213-218. |
| [8] | BACKES M, HRITCU C, MAFFEI M. Type-checking zero-knowledge[C]//Proceedings of the 15th ACM Conference on Computer and Communications Security. New York, USA: ACM, 2008: 357-370. |
| [9] | 杨庆, 陈桂明, 刘鲭洁, 等. 基于测地线距离的核主元分析在齿轮泵故障识别中应用[J]. 上海交通大学学报, 2011, 45(11): 1632-1636.YANG Qing, CHEN Guiming, LIU Qingjie, et al. Application of kernel principal component analysis based on geodesic distance in pattern recognition of gear pump[J]. Journal of Shanghai Jiao Tong University, 2011, 45(11): 1632-1636. |
| [10] | YUAN Lu, SUN Jian, QUAN Long, et al. Image deblurring with blurred/noisy image pairs[J]. ACM Transactions on Graphics (TOG), 2007, 26(3): 1. |
| [11] | CRISTIANINI N, SHAWE-TAYLOR J. 支持向量机导论[M]. 李国正, 王猛, 曾华军, 译. 北京: 电子工业出版社, 2004. |
| [12] | DU Chengjin, SUN Dawen. Multi-classification of pizza using computer vision and support vector machine[J]. Journal of Food Engineering, 2008, 86(2): 234-242. |



