当前各电信企业市场竞争越演越烈,为了提高客户忠诚度,迫切要求企业借助于对日益庞大的历史数据进行分析,制定更好的技术方案和营销策略。然而影响客户忠诚度的因素非常复杂,营销人员不通晓技术,技术人员又不精于营销,且数据挖掘是目前最有效的数据分析手段之一,用于发现大量数据所隐含的各种规律[1],因此选择一种合适的数据挖掘方法极为重要。目前常用的方法是关联规则挖掘[2],因为其能够比较直观地得出各因素之间的关系,而且操作过程简单,结果的可解释性强[3]。但是,现有的关联规则挖掘方法均无法进一步发现隐藏在属性内部的相关规律,并且在面向海量数据挖掘时效率很低。
目前用于电信客户流失预测的方法主要可分为3类[4]:第1类方法以传统的统计学理论为基础,主要包括聚类、贝叶斯分类器、决策树和逻辑回归等。如Kim等[5]曾采用逻辑回归方法对韩国部分移动客户进行了流失预测分析,探讨了韩国移动电信市场相关因素在客户流失和忠诚度之间的关系,为保持客户的忠诚度提供了帮助。第2类方法以人工智能理论为基础,主要包括人工神经网络和进化学习等。如Mozer等[6]曾采用人工神经网络方法结合数据抽样等方法建立了客户流失预测模型,并为某电信公司进行了客户流失预测,通过与决策树等方法对比,发现采用该方法产生的关联规则预测效果更好,准确率更高。第3类方法以统计学习理论为基础,其典型代表为支持向量机方法。如邝涛等[7]采用基于代价敏感学习的支持向量机模型对某电信公司的客户数据进行挖掘,并通过与神经网络等方法对比,发现该方法能获得较高的预测精度和覆盖率,并能在某种程度上解决了数据集非平衡性等问题。
尽管以上3类方法被大量使用,但它们都忽略了属性内在结构之间的细粒度的相关规律,即存在关联规则不够精细的问题;并且在用于海量数据分析时计算量大、效率低,难以及时反映客户的流失倾向,因此不能完全满足当前电信应用的需求。因此,本文的思路是把每个独立的属性“打碎”,即分解得到细粒度的“属性片段”,以提高关联规则的fine精度[8],再基于属性片段采用合适的关联规则挖掘算法,最后得到的关联规则要易于对海量数据实施并行计算提高效率,从而可以更好地及时定位影响客户流失的关键因素,或发现一些隐藏的关键规律,使其能在电信客户流失预测中具有更大的应用空间。
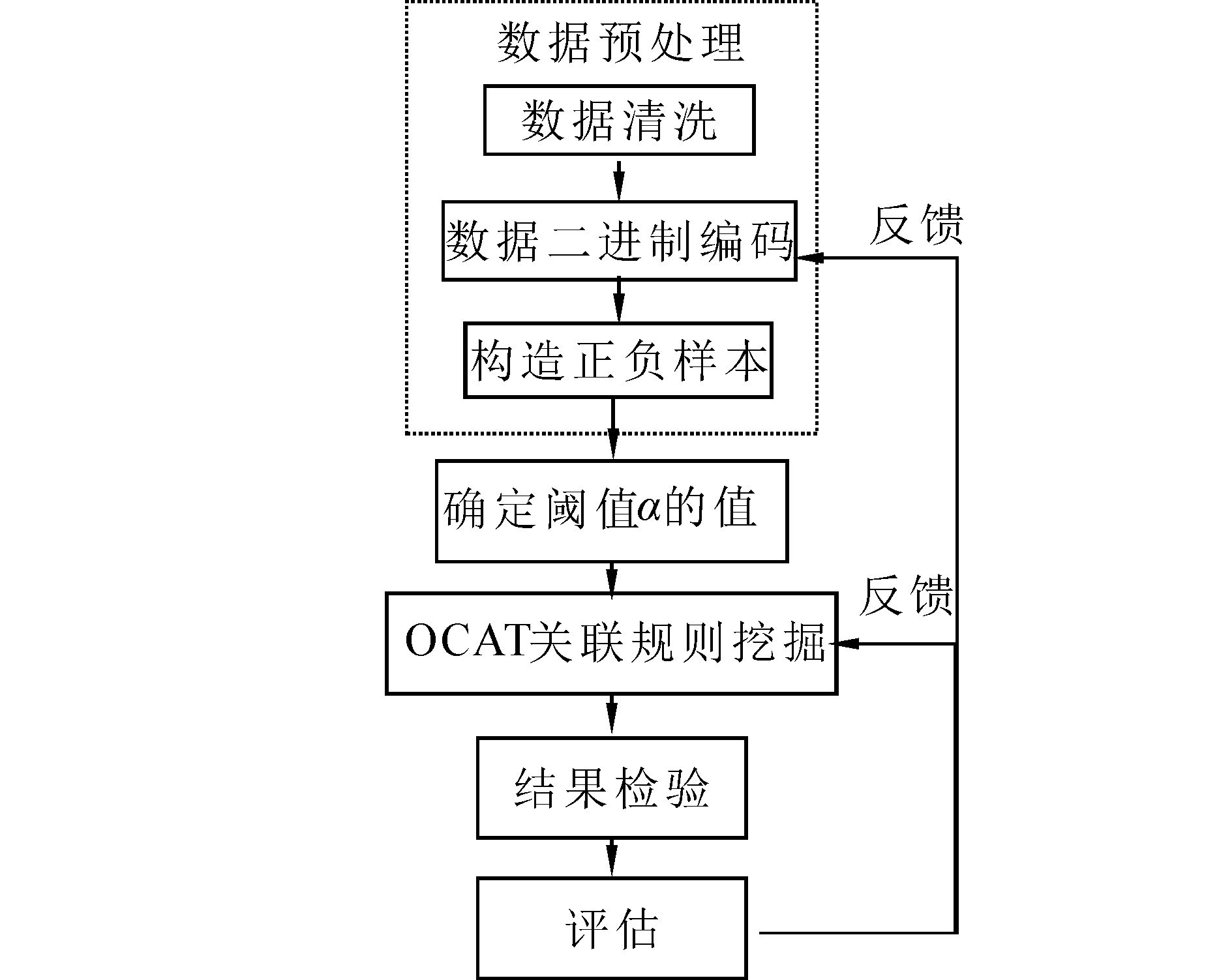
1 电信数据挖掘分析与改进为了得到属性内在相关规律及方便实现并行运算,采用了基于逻辑的细精度关联规则挖掘方法。首先提出了与领域相关的属性分解方法,即对属性值域进行合适的分类以得到“属性片段”,再对每个分类进行二进制编码。而这样变化后的数据并不适合采用决策树和聚类等传统方法进行处理,于是我们结合了E. Triantaphyllou提出的基于逻辑的OCAT方法[9]35-45进行关联规则挖掘。这种方法的核心是通过某种基于逻辑的方法寻找一系列子式,再由这些子式合取得到关联规则表达式,该表达式由二进制化后的“属性片段”构成,不仅能直观地展现属性的内部结构和内涵,而且这种由合取范式表示的关联规则特别适合采用并行计算进行海量数据分析,从而提高运算效率。图 1展示了该方法的具体步骤:数据预处理(数据清洗、数据二进制编码和正负样本构造)、关联规则的挖掘、结果检验以及评估反馈。
|
| 图 1 细精度关联规则挖掘流程 Fig. 1 Process of fine-grained association rule mining |
文中数据集为某电信运营商某地区数据仓库中的客户原始历史数据,总共有176 921条记录,其中正常客户记录为156 885条,流失客户记录20 036条。
1)数据清洗与属性变换。
首先删除有效值较少的属性或记录,以及非法的记录。其次,在电信客户流失的应用背景下,需要研究能够反映客户消费承受能力、消费习惯和消费行为的属性相关性,同时用文献[10]的经验做支撑,为了能够准确地覆盖影响客户流失的因素,构建了月消费比率ri(上一个月与本月的消费比值)、年度本地通话费用(year_local_fee)、未消费月份数(non_fee)3个属性。在实验中选用了r1(2008年12月的消费额/2009年1月的消费额)、r2(2009年1月的消费额/2009年2月的消费额)、f0902e(2009年2月的消费额)、year_local_fee等5个属性作为特征属性。
2)数据二进制编码。
考虑到属性值域分类的语义差别,及其与客户流失问题的相关性差别,采用了与领域相关的二进制编码方法将属性“掰碎”,即根据记录的取值相关性进行分类。经过分析,发现实验用到的电信用户数据集具有典型的密度特性,因此采用了基于密度的可以快速发现任意形状类的DBSCAN分类算法[11]完成从“属性”到“属性片段”的分解。另外,此数据集不同属性值域区间的差异较大,这可能会影响分类的效果,因此还需要对这些属性进行常用的归一化处理。具体的步骤是:首先使用mapminmax(x,min,max)函数将值域归一到区间[0,1],其次以每个属性数据结合函数ones(n,1)产生的数据作为输入x(其中n为样本的个数),通过经验以及多次实验确定较优的参数。结果集中可能会存在孤立点,较优的参数能够减少孤立点的个数,并且产生较为合理的分类。在实际应用中,孤立点的数量往往远小于正常数据[12],因此其影响比较小,故本文就近将孤立点分配至临近的区间(相应的孤立点处理方法作为后续工作)。经过DBSCAN运算后,便得到了属性分类,即“属性片段”,这些分类结果直接反映了其属性值自然特有的内在规律,由事物本身决定,不受人为控制,因此对后续进一步分析隐藏在它们之间的相关性有重要的指导作用。最后,再根据分类的个数,使用若干二进制位对属性片段进行二进制编码。以属性year_local_fee为例,其被划分为7个区间,包含65个孤立点,将这些孤立点按照就近原则并入7个区间内,故以3位二进制位来表示,如表 1所示。实验中各属性的分类数如表 2所示。
| 区间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 编码 | 000 | 001 | 010 | 011 | 100 | 101 | 110 |
| 属性 | 分类数 |
| non_fee | 3 |
| year_local_fee | 7 |
| r1 | 7 |
| r2 | 5 |
| f0902e | 8 |
3)正负样本的构造。
首先,根据数据集中churn标志位(标志客户流失信息的属性)的值,将整个数据集的用户划分为已经流失的客户(churn值为0)和未流失的客户(churn值为1)2类。其次,为了得到关联规则挖掘中需要的训练集和检验集,实验分别随机抽取未流失客户和已流失客户中四分之三的数据[13]来构造训练集数据的正负样本(用E+和E-来分别表示正样本和负样本),剩余的数据用作检验集。最后,通过前后10次进行随机抽取得到正负样本,并分别计算结果,进一步验证数据挖掘结果的稳定性、可信性和鲁棒性。在构造E+和E-时,采用了如表 3所示的属性排列顺序及其编码对应关系。
| 属性 | 二进制编码 |
| non_fee | A1 |
| A2 | |
| year_local_fee | A3 |
| A4 | |
| A5 | |
| r1 | A6 |
| A7 | |
| A8 | |
| r2 | A9 |
| A10 | |
| A11 | |
| f0902e | A12 |
| A13 | |
| A14 |
经过数据预处理得到的二进制数据不能采用决策树和聚类等传统方法处理,同时为了让关联规则易于实施并行计算,实验中采用了OCAT方法,该方法每次产生一条最优子式(接受全部正样本,拒绝尽可能多的负样本),最终将子式通过合取操作得到关联规则。但是,OCAT产生单个子式的过程中剪枝的数量较少,导致收敛速度缓慢,并且需要存储大量的叶子结点的限界,导致运算时耗费了极大的时间和空间。因此,实验中最终引入了启发式规则[9]73-80进行快速剪枝,将时间复杂度从指数级别降到多项式级别,这将非常适合数据量庞大的电信数据挖掘。
启发式方法中根据POS(ak)/NEG(ak)的比值逆序排列属性(片段)ak(ak为Ai或¬Ai)形成有序集合A,挑选A中前α(%)(阈值)的元素生成待选集合L。关联规则的构造过程即不断地从待选集合L中随机选出属性(片段)ak加入子式的过程,该过程持续到关联规则完成或集合L为空。若α值过小,则关联规则不完整,导致预测结果准确度下降;反之,若α值过大,则对客户流失影响很小的属性(片段)可能会包含在关联规则中,从而导致关联规则的子句过长、数量过多,以及属性间的相关性不够强。由于二进制编码方法和关联规则挖掘过程的随机性都会影响所生成的关联规则的准确性,故需要在实验过程中进行多级反馈和修正。基于启发式的OCAT算法流程如下。
输入:正负样本E+和E-。 //E+、E-分别是未流失和已流失客户数据集。
输出:程序执行多次所得最优的关联规则C,其规范形式为式(1)所示,其中析取子式由属性片段析取得到,并能保证子式的数量n最少,且子式中属性片段的数量也是最少。

初始化E+、E-和C=∅
Do While (E-≠∅)
重置集合A,Ci=∅; //A为二进制编码
属性片段ak的集合,ak为Ai或¬Ai
Do While (E+≠∅)
1)根据POS(ak)/NEG(ak)的比值逆序排列A中的元素ak(如果NEG(ak)为零,则将POS(ak)作为它的值);
2)选择有序集A中前α(%)的元素生成待选集合L;
3)从L中随机选择属性ak加入到Ci中;
4)E+←E+-E++(ak); //E+(ak)为包含ak时Ci所能接受的E+的中的元素集合
5)A←A-ak; //将ak从集合A中剔除
6)对所有ak∈A重新计算POS(ak)的值; Repeat
7)C←Ci∧C; //将子式Ci合取到关联规则C中
8)E-←E--E-(C); // E- (C)为C目前所能拒绝的E-中的元素集合
9)重置E+;Repeat
2 细精度关联规则挖掘为了验证上述方法在预测客户流失过程中的可行性及有效性,我们设计并实现了各个过程。实验环境为1)CPU/内存/硬盘:AMD Athlon(tm)Ⅱ X2215/DDR2 4 GB/320 GB 7 200 转/min;2)平台/环境/语言Windows 8.1 64 bit操作系统、Microsoft Visual Studio 2013/C、C#。
为了验证加入启发式规则后算法的收敛效果,在相同正负样本和相同环境下进行了时间与空间消耗的对比实验。通过多次实验,选取的负样本基数为50,这种大小的样本空间可以让OCAT方法的耗时不会太大,又能明显比较出2种方法在相同数据集上的时间耗费差异。在改变正样本的基数时,分别使用上述2种方法的运算时间对比如图 2(a)所示。同理,将正样本基数固定为10,负样本基数从50开始,每次增加10条负样本记录,一直到100条,此时得到的运算时间对比如图 2(b)所示。此外,在300条正样本与100条负样本情况下,对二者的内存占用情况进行对比,其中图 2(c)为未运行程序时的内存占用,图 2(d)与图 2(e)分别为使用OCAT方法与加入启发式方法后的内存占用情况。

|
| 图 2 实验结果 Fig. 2 Experiment results |
从图 2(a)~(e)可以看出,加入启发式规则之后的方法比OCAT方法所消耗的时间与空间都大大减少,图 2(f)描述了不同的阈值α值对预测准确度的影响,体现了其重要性。最后,10次实验所得的关联规则之一如式(2)所示。
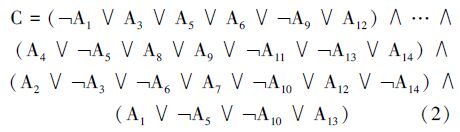
该表达式为关联规则的布尔表达式,它由4条析取范式的子式经过合取操作得到,其中每条子式均能接受所有的正样本而拒绝若干负样本,所有子式合取而成的关联规则能接受所有正样本并且拒绝所有负样本。这一结果具有如下特点:
1)反映了一些新的规律。以子式(¬A1∨A3∨A5∨A6∨¬A9∨A12)为例,对照表 1分析得出属性non_fee与其他属性Year_local_fee、r1、r2、f0902e的“内在片段”的相关性,即“属性+片段->片段”或“片段+片段->属性”,而传统的关联规则只能发现属性与属性的相关性,即“属性+属性->属性”。
2)运算效率高。以子式(¬A1∨A3∨A5∨A6∨¬A9∨A12)为例,其仅有6个原子项,因此运行较快。而由于上述关联规则为合取范式,以“∧”为连接词构成,因此用这种形式的规则检验海量数据时可采用高度并行计算的方法,进一步了减少时间开销。
3)剖析了属性内部结构与内涵。以子式(¬A1∨A3∨A5∨A6∨¬A9∨A12)为例,其等价于(A1∧¬A3∧¬A5∧¬A6∧A9) ⇒ A12,体现的已非属性之间的关联,而是属性片段与片段的相关性,即片段A12的取值取决于片段A1、A3、A5、A6和A9。这一结果有利于公司决策者制定更为精准的市场策略。
4)提高了fine精度。10次实验所得到的关联规则分别对应10条主合取范式,这些主合取范式可以使用矩阵形式表示,式(2)的主合取范式如表 4所示。其余9条主合取范式与表 4所示的主合取范式的相似度在86.4%~90.2%,体现了结果的稳定性、可信性和鲁棒性,说明了提升fine精度的合理性。
| 编码 | SubF1 | SubF2 | SubF3 | SubF4 |
| A1 | 0 | △ | △ | 1 |
| A2 | △ | △ | 1 | △ |
| A3 | 1 | △ | 0 | △ |
| A4 | △ | 1 | △ | △ |
| A5 | 1 | 0 | △ | 0 |
| A6 | 1 | △ | 0 | △ |
| A7 | △ | △ | 1 | △ |
| A8 | △ | 1 | △ | △ |
| A9 | 0 | 1 | △ | △ |
| A10 | △ | △ | 0 | 0 |
| A11 | △ | 0 | △ | △ |
| A12 | 1 | △ | 1 | △ |
| A13 | △ | 0 | △ | 1 |
| A14 | △ | 1 | 0 | △ |
| 注:符号“△”表示取0和1均可,SubF1有256条,SubF2有128条,SubF3有128条,SubF4有1 024条 | ||||
5)得到了更直观、清晰的语义解释。以子式 (A1∨¬A5∨¬A10∨A13)为例,若某一客户数据使该子式结果为0(¬A1、¬A5、¬A10、A13取值均为0),则可以预测该用户为流失客户。根据A1、¬A5、¬A10、A13的取值映射到表 3,可以得出在non_fee的3区间、year_local_fee的2,4,6区间、r2的3,4区间与fe0902的1,3,5,7区间共同影响客户流失,根据区间与属性值对应的关系可知,客户数据符合表 5取值的均为流失客户。
| 属性 | 取值范围 |
| non_fee | 6~12 |
| year_local_fee | 30~50 |
| 70~88 | |
| 92~133 | |
| r1 | 0.320~0.416 |
| r2 | 0~20 |
| 25~29 | |
| 34~50 | |
| 48~68 | |
| f0902e | 6~12 |
针对决策树等常规关联规则方法在电信客户流失预测中遇到的属性相关性不够精细,处理大规模数据运算效率低的问题,本文采用了基于逻辑的细精度关联规则方法。该方法从逻辑学角度,通过与领域相关的二进制化技术对属性进行分解,并用得到的二进制数据构造训练集的正负样本,再使用OCAT方法对正负样本进行挖掘得出关联规则。然而,实验过程中耗费了极大的时间与空间,这表明直接用该方法进行海量电信数据的挖掘是不理想的。因此引入了启发式规则对其进行改进,将时间复杂度从指数级别降低到多项式级别。最后通过实验结果分析,验证了该方法能进一步体现属性的内在结构、内涵及隐藏的细粒度的相关规律,提高了关联规则的fine精度,并且这种由合取范式表示的关联规则特别适合实施并行计算,有利于大规模电信数据的处理,因此该方法是满足目前电信行业需求的一种较理想的数据挖掘方法。
尽管上述方法取得了不错的效果,但是对于不同数据集在具体应用时还存在一些困难,如如何更好地结合领域知识和数学方法对属性进行分解及二进制编码进而构造正负样本,如何寻找更好的启发式规则提高运算性能等。另外,当数据样本比较小的时候,得到的关联规则的准确率不够高,但在数据样本足够大的情况下,关联规则预测准确率会比较理想。在今后的工作中,将努力完善本方法的各个环节,同时找到适用本方法的数据集特征,以应用到更合适的实际问题中。
| [1] | 朱扬勇, 熊赟. DNA序列数据挖掘技术[J]. 软件学报, 2007, 18(11): 2766-2781.ZHU Yangyong, XIONG Yun. DNA sequence data mining technique[J]. Journal of Software, 2007, 18(11): 2766-2781. |
| [2] | 贺炜, 潘泉, 陈玉春, 等. 关联规则挖掘与因果关系发现的比较研究[J]. 模式识别与人工智能, 2005, 18(3): 328-333.HE Wei, PAN Quan, CHEN Yuchun, et al. A Comparison between association rule data mining and causal discovery[J]. Pattern Recognition and Artificial Intelligence, 2005, 18(3): 328-333. |
| [3] | 毛宇星, 陈彤兵, 施伯乐. 一种高效的多层和概化关联规则挖掘方法[J]. 软件学报, 2011, 22(12): 2965-2980. MAO Yuxing, CHEN Tongbing, SHI Bole. Efficient method for mining multiple-level and generalized association rules[J]. Journal of Software, 2011, 22(12): 2965-2980. |
| [4] | 夏国恩. 客户流失预测的现状与发展研究[J]. 计算机应用研究, 2010, 27(2): 413-416.XIA Guoen. Research on current situation and development of customer churn prediction[J]. Application Research of Computers, 2010, 27(2): 413-416. |
| [5] | KIM H S, YOON C H. Determinants of subscriber churn and customer loyalty in the Korean mobile telephony market[J]. Telecommunications Policy, 2004, 28(9/10): 751-765. |
| [6] | MOZER M C, WOLNIEWICZ R, GRIMES D B, et al. Predicting subscriber dissatisfaction and improving retention in the wireless telecommunications industry[J]. IEEE Transactions on Neural Networks, 2000, 11(3): 690-696. |
| [7] | 邝涛, 张倩. 改进支持向量机在电信客户流失预测的应用[J]. 计算机仿真, 2011, 28(7): 329-332. KUANG Tao, ZHANG Qian. Application of telecom customer churn prediction based on improved support vector machine[J]. Computer Simulation, 2011, 28(7): 329-332. |
| [8] | FOX C, LAPPIN S. Foundations of intensional semantics[M]. New York: Wiley-Blackwell, 2008: 78-82. |
| [9] | TRIANTAPHYLLOU E. Data mining and knowledge discovery via logic-based methods: theory, algorithms, and applications[M]. New York: Springer, 2010. |
| [10] | 蒋盛益, 李霞, 郑琪. 数据挖掘原理与实践[M]. 北京: 电子工业出版社, 2013: 211-212. |
| [11] | 王鑫, 王洪国, 王珺, 等. 数据挖掘中聚类方法比较研究[J]. 计算机技术与发展, 2006, 16(10): 20-22.WANG Xin, WANG Hongguo, WANG Jun, et al. Comparison of clustering methods in data mining[J]. Computer Technology and Development, 2006, 16(10): 20-22. |
| [12] | 张净, 孙志挥, 杨明, 等. 基于网格和密度的海量数据增量式离群点挖掘算法[J]. 计算机研究与发展, 2011, 48(5): 823-830.ZHANG Jing, SUN Zhihui, YANG Ming, et al. Fast incremental outlier mining algorithm based on grid and capacity[J]. Journal of Computer Research and Development, 2011, 48(5): 823-830. |
| [13] | 胡文瑜, 孙志挥, 吴英杰. 数据挖掘取样方法研究[J]. 计算机研究与发展, 2011, 48(1): 45-54. HU Wenyu, SUN Zhihui, WU Yingjie. Study of sampling methods on data mining and stream mining[J]. Journal of Computer Research and Development, 2011, 48(1): 45-54. |



