2. 哈尔滨船舶锅炉涡轮机研究所, 黑龙江 哈尔滨 150036
2. Harbin Marine Boiler and Turbine Research Institute, Harbin 150036, China
智能投球机器人是一个由微处理器控制,集环境感知、避障、行走、投球等功能于一体的智能机器人。对于投球机器人来说,运动控制的目的就是使之能精确并且快速地实现机械臂转角运动。传统的机器人运动控制常采用PID控制器[1]。由于各种干扰因素,机器人的运动具有时变、非线性、干扰大和不确定等特性,传统的PID控制器已不能达到较好的控制效果[2]。近几年,机器人智能控制在理论和应用方面都取得较大的进展[3]。在模糊控制方面,由J. J. Buckley等论证了模糊系统的逼近特性[4],E. H. Mamdan首次将模糊理论运用于一台实际机器人,使模糊控制技术在机器人中的应用得以展现[5]。文献[6]针对移动机器人在传统控制器控制下自主运动时出现的不稳定状况,将模糊控制策略引入移动机器人运动控制系统中。通过分析比较不同的控制方法,设计了由速度误差率和速度误差变化率为输入、电机输出功率为输出的双输入单输出模糊逻辑控制器。文献[7]模仿人工预瞄驾驶行为,提出了移动机器人运动控制的模糊控制方法,实验表明,该模糊控制方法可保证移动机器人快速、准确地沿着各种参考轨迹行走,且具有良好的鲁棒性。文献[8]在智能轮椅机器人中使用超声波的探测距离作为输入信号,经模糊控制技术处理后,输出机器人左右轮的转动速度来实现超声波避障。
本文首先对二连杆投球机器人进行运动学建模,然后在此基础上对机器人的控制方法进行了研究,通过PID和模糊PID2种控制方法,实现二连杆投球机器人运动轨迹的有效控制,用MATLAB软件进行仿真,并对仿真结果进行对比分析。
1 二连杆投球机器人的运动学建模 1.1 二连杆机械臂机械手臂是机器人重要构成部件。图 1为二杆机械臂结构图,其中θ1和θ2分别为关节1、2转角,l1和l2分别为第1、2根杆的长度,r1为关节1到第1根杆质心的距离,r2为关节2到第2根杆质心的距离,Mpl为负载质量。
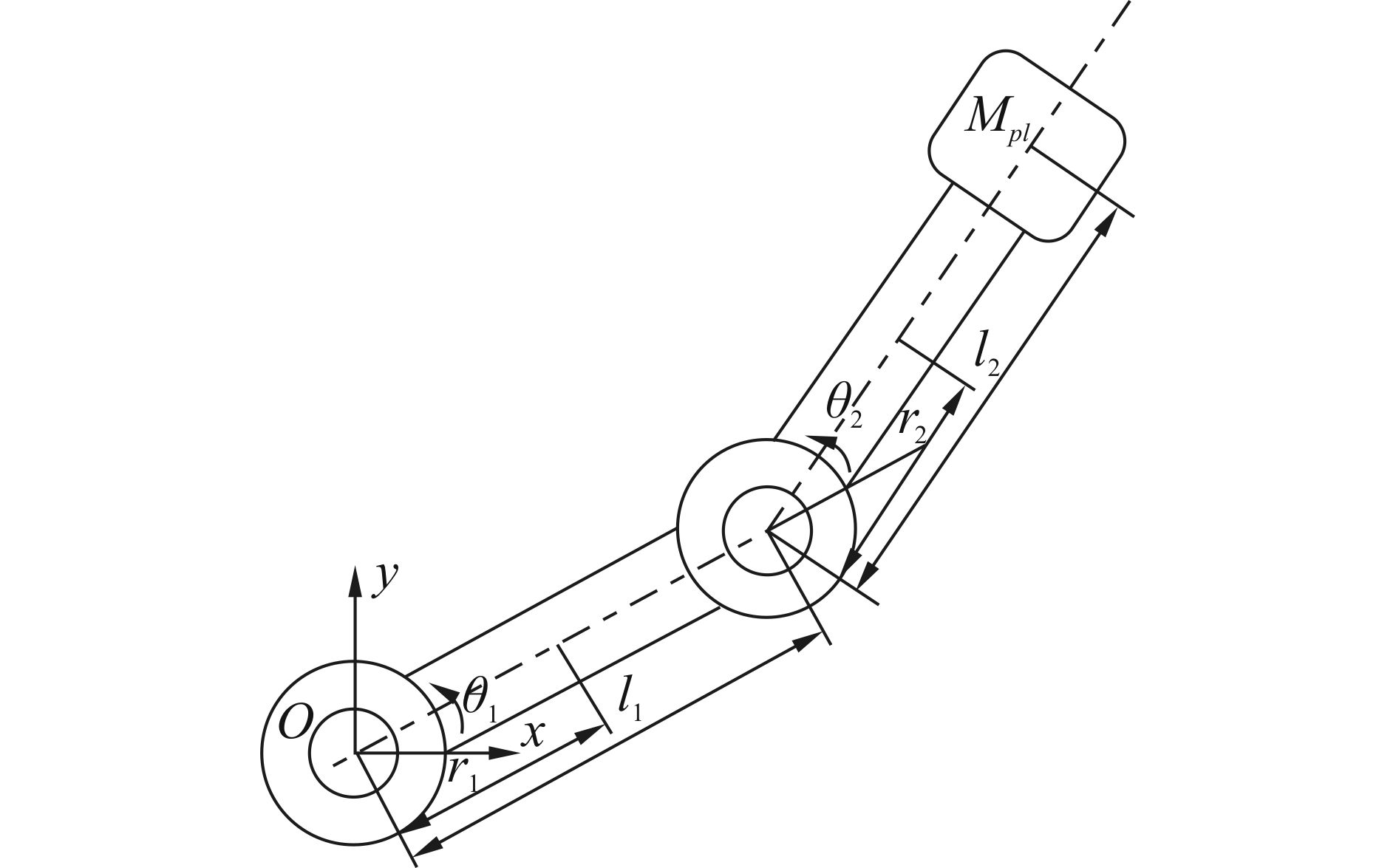
|
| 图 1 二连杆机械臂结构 Fig. 1 Dual-arm mechanical structure |
式(1)是二连杆机械臂的矢量方程,其中R1、R2是沿r1和r2方向上的矢量,Rpl为合成矢量。由于在二连杆机械臂中,各连杆的长度保持不变,但它们各自的方位却随机构的运动而改变,所以矢量方程对时间求导将闭环矢量方程分解成2个标量表达式,分别沿x、y方向分解。

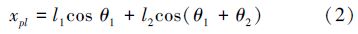
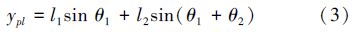
对末端坐标进行积分得到末端速度方程:
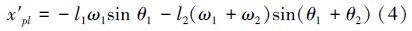

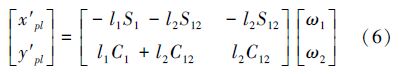
对二连杆机械臂末端速度方程(3)~(4)进行求导得到末端加速度方程:



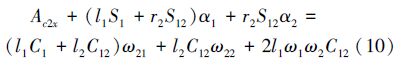
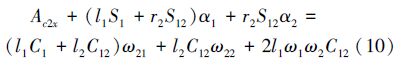
首先,对二连杆平面投球机器人的第1根连杆应用牛顿定律[11],受力分析如图 2所示。
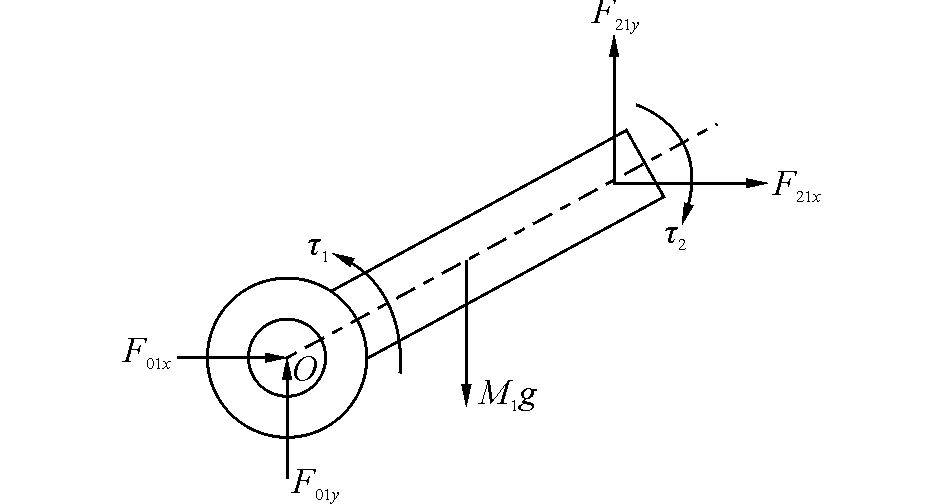
|
| 图 2 第1根连杆受力分析 Fig. 2 The first arm force analysis |
图 2中,F01x、F21x分别代表第1根杆2端所受x方向的力,F01y、F21y分别代表第1根杆2端所受y方向的力,M1为第1根杆的质量,τ1、τ2分别为关节1和关节2的控制力矩。
由图 2可以推导出机械臂第1杆的运动方程:
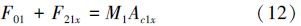
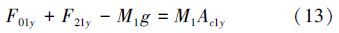
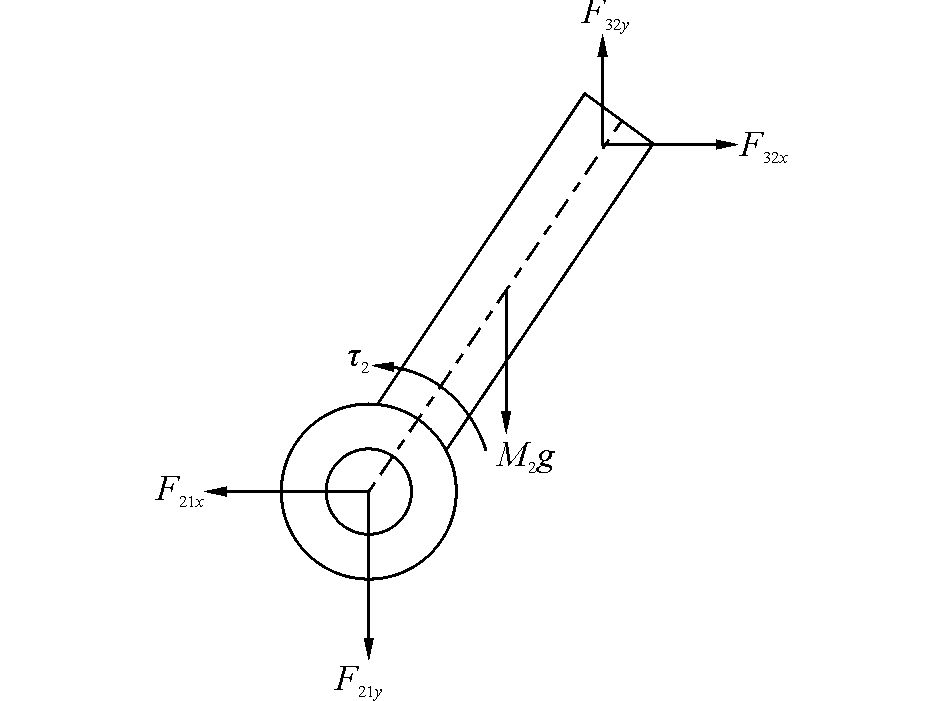
其次,对二连杆机械臂的第2根连杆进行受力分析,如图 3所示。
|
| 图 3 第2根连杆受力分析 Fig. 3 The second arm force analysis |
图 3中,F21x为第2根杆2端所受x方向的力,F21y为第2根杆2端所受y方向的力,M2为第2根杆的质量,F32x为第2根杆所受x方向的力,F32y为第2根杆所受y方向的力。第2根杆的3个运动方程为:
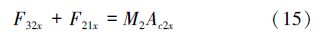
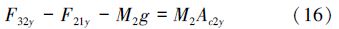
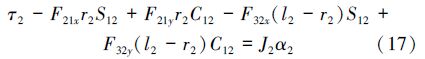
作用在机器人上的有效载荷的变化直接与2个连杆相联系,因此可将其与连杆一起表示,如图 4所示。其中F32x为末端所受x方向的力,F32y为末端所受y方向的力,Mplg为负载的质量。

|
| 图 4 负载受力分析 Fig. 4 Load force analysis |
有效载荷的质量是由二连杆机械臂举起的重物所决定的,将加载物视为集中质量,可以得到以下方程:
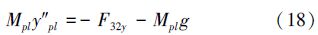
将2个关节电机输入转矩作为输入,联立运动约束方程(6)~(10)和运动学方程(11)~(18),推导出约束矩阵方程(19):



分别采用PID控制和模糊PID控制对二连杆投球机器人进行运动轨迹控制。
2.1 PID控制PID控制策略其结构简单、稳定性好、可靠性高[12]。式(20)为PID控制标准公式,其中U(t)为PID控制器输出,Kp为比例放大系数,Ti为积分常数,Td为微分放大系数,e为偏差信号。
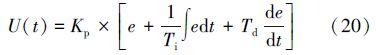
PID参数设置:首先确定比例增益Kp,而后确定积分时间常数Ti,最后确定微分时间常数Td,通常为0即可。
2.2 模糊PID控制 2.2.1 模糊控制基本原理模糊控制的核心是模糊控制器,而模糊控制器的关键是模糊控制规则的确定,即模糊控制规则表[13]。模糊控制系统框图如图 5所示,把误差e及其变化率ec作为模糊控制器的输入,把控制量u作为模糊控制器的输出,得


|
| 图 5 模糊控制器基本结构 Fig. 5 The basic structure of the fuzzy controller |
二连杆平面机器人2个关节预定角度θ1d和θ2d与实际角度θ1和θ2的误差e及其变化率ec作为控制器输入,输出为驱动关节转矩τ。
2.2.2 输入量的模糊化精确输入量e和ec分别乘以量化因子ke和kec以转换到各自的论域范围。设模糊控制器的输入量标准域均为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。输入量论域划分成7个模糊子集,即{NB,NM,NS,ZO,PS,PM,PB}。模糊子集的隶属函数采用高斯函数,函数曲线如图 6所示。

|
| 图 6 隶属函数曲线 Fig. 6 Membership functions curve |
规则选取的总体原则是:当误差较大时,选择控制量以消除误差为主;当误差较小时,选择控制量要防止超调,以系统的稳定性为主。
输出变量与输入变量取一样的模糊子集,即u={NB,NM,NS,ZO,PS,PM,PB},同样采用高斯隶属函数。e和ec分别定义为7个模糊子集、49条规则,如表 1所示。
| e | u | ||||||
| ec=NB | ec=NM | ec=NS | ec=ZO | ec=PS | ec=PM | ec=PB | |
| NB | PB | PB | PB | PB | PM | 0 | 0 |
| NM | PB | PB | PB | PB | PM | 0 | 0 |
| NS | PM | PM | PM | PM | 0 | NS | NS |
| ZO | PM | PM | PS | 0 | NS | NM | NM |
| PS | PS | PS | 0 | NM | NM | NM | NM |
| PM | 0 | 0 | NM | NB | NB | NB | NB |
| PB | 0 | 0 | NM | NB | NB | NB | NB |
根据二连杆机械臂在重力作用下的受力情况,如果让机器人从任何初始位置开始运动,将输入的值设置为零,那么二连杆机械臂将在自身重力作用下下落,最后到达2个连杆都在一条铅垂线上的位置。参考图 1中节点角的定义,此时相应的节点角度θ1=-π/2和θ2=0。表 2给出二连杆平面机器人的惯性参数和几何参数。
| 参数 | 取值 |
| M1/kg | 2.5 |
| M2/kg | 2.8 |
| Mpl/kg | 0.05 |
| l1/m | 1.0 |
| l2/m | 0.5 |
| r1/m | 0.8 |
| r2/m | 0.1 |
| J1/(kg·m2) | 0.15 |
| J2/(kg·m2) | 0.05 |
图 7是一个Simuarm模型[14]的原理框图。仿真调用robot.m来求解联立约束矩阵,采用一种线性摩擦力模型,在该模型中,抵抗输入扭矩的摩擦力矩与转速成正比。2个标“Damping”的增益模块表示由于轴承和电动机的粘滞阻尼而产生的速度损失。

|
| 图 7 两连杆机器人的Simuarm仿真模型 Fig. 7 Simuarm simulation model of dual-arm robot |
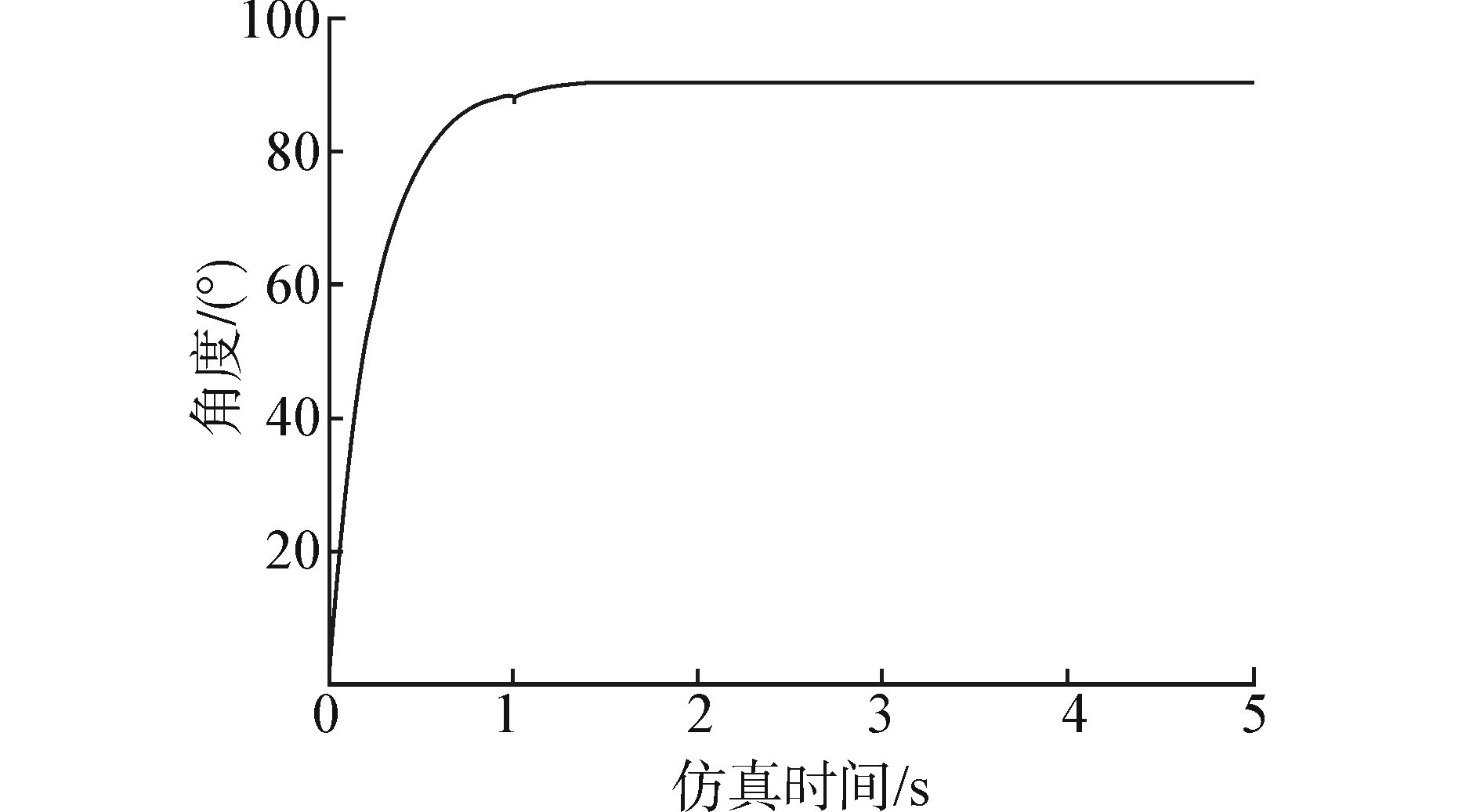
仿真初始条件:θ1=0和θ2=-π/2,末端位置:xpl=1.0,ypl=0.8,与此同时,积分求解器的初始条件也是相容的。仿真结果如图 8所示。图 8给出了关节转角θ1和θ2的转角曲线,在经过一定的仿真时间后,二连杆机械臂运动趋于稳定,θ1为-π/2,θ2为0,与机械臂在自重下试验姿态相吻合。
|
| 图 8 关节转角θ1和θ2的变化曲线 Fig. 8 Curve of joint angle θ1 and θ2 |
在对二连杆机械臂进行建模与仿真基础上加入PID控制模块来控制各个节点电动机的位置,控制二连杆机械臂无震荡的从一个节点快速移动到另一个节点。选择Simarm中的SimMechanics工具箱进行PID控制及模糊PID控制的仿真。
3.2.1 控制模型图 9为二连杆投球机器人的SimMechanics仿真图[15]。Ground为机架模块,barAB、barBC代表第1、2根杆,A、B分别代表转动副模块,Joint Sensor1代表运动副传感器模块,Joint Actuator为运动驱动模块。

|
| 图 9 二连杆机器人仿真框图 Fig. 9 Simulation block of dual-arm robot |
在系统中首先加入PID控制器[16],控制器输入二连杆平面机器人两关节预定角度θ1d和θ2d与实际角度θ1和θ2的误差e,输出为驱动关节转矩τ。
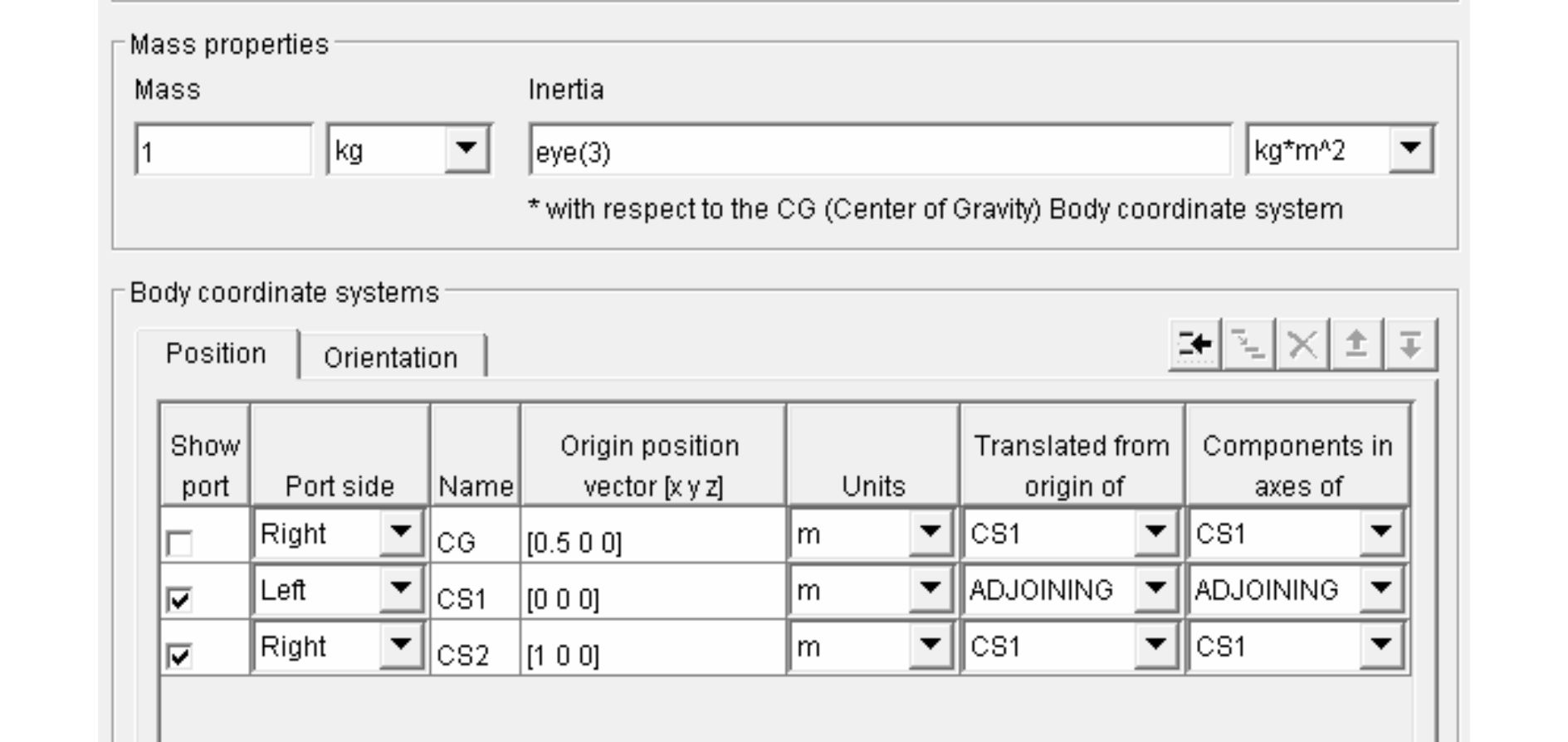
仿真模型建立后,要对每个模块都进行参数的设置。以AB杆为例,见图 10。双击barAB,填入参数:杆的质量、刚体坐标和质心位置。所有参数设置完成后,再设置允许每个连杆的旋转角度。在此,设置第1根杆旋转90°,第2根杆旋转135°。
|
| 图 10 AB杆模型参数 Fig. 10 Model parameters of AB arm |
得到二连杆机械臂的旋转角度曲线,根据上节所述方法调节PID参数,得到理想的响应曲线。图 11为经过PID调节后二连杆平面投球机器人的旋转角度情况。可以看到,经过PID调节后,系统可以实现快速启动,并且缩短了时间,快速地进入新的稳定状态。

|
| 图 11 两连杆机械臂旋转角度 Fig. 11 Rotation angle of dual-arm |
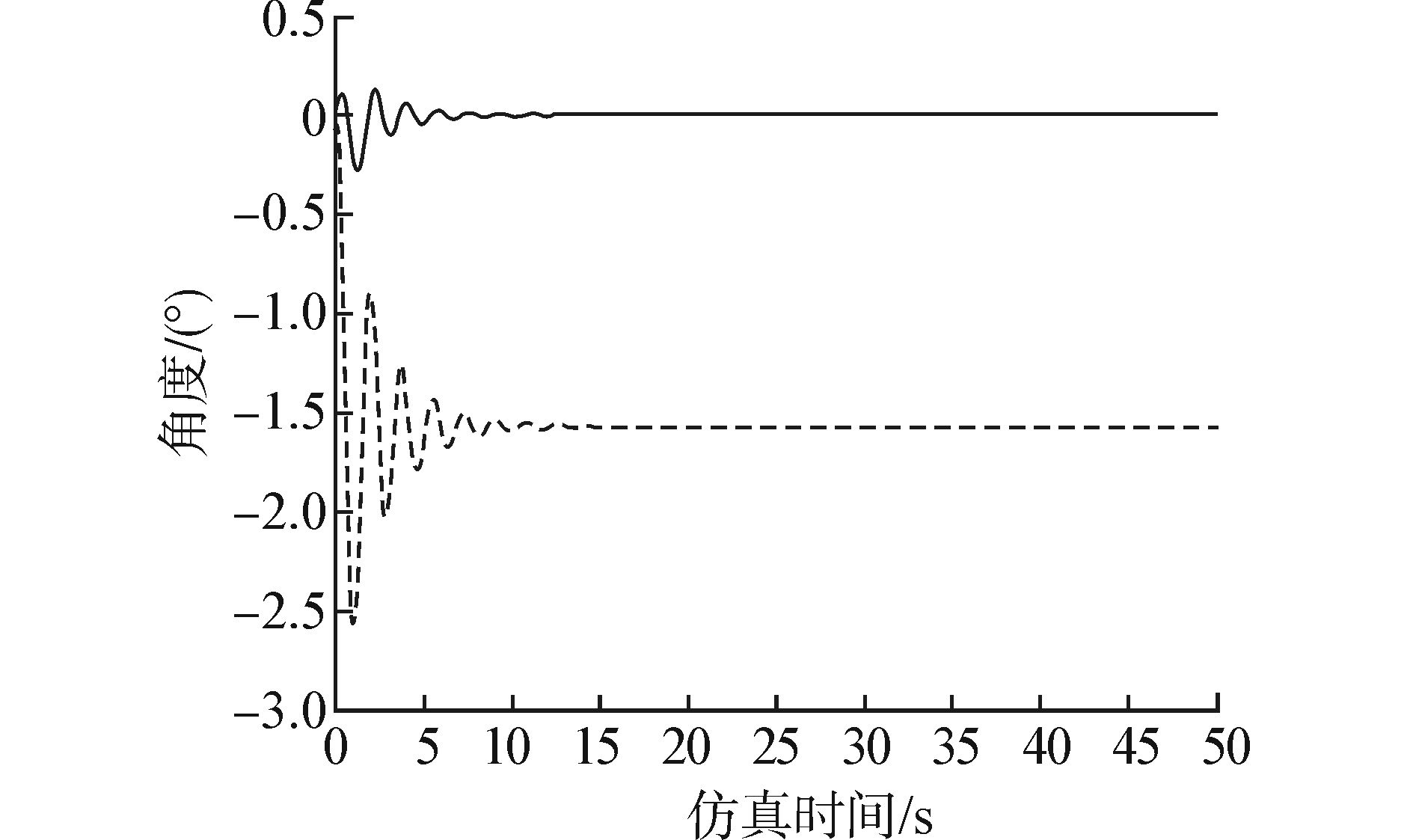
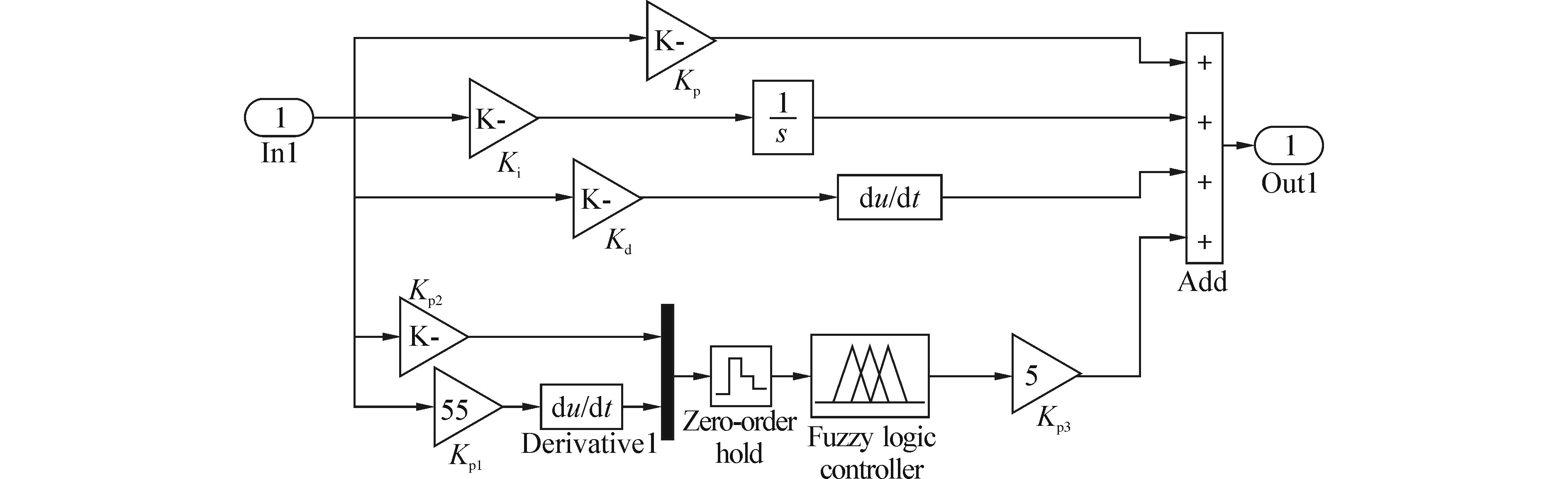
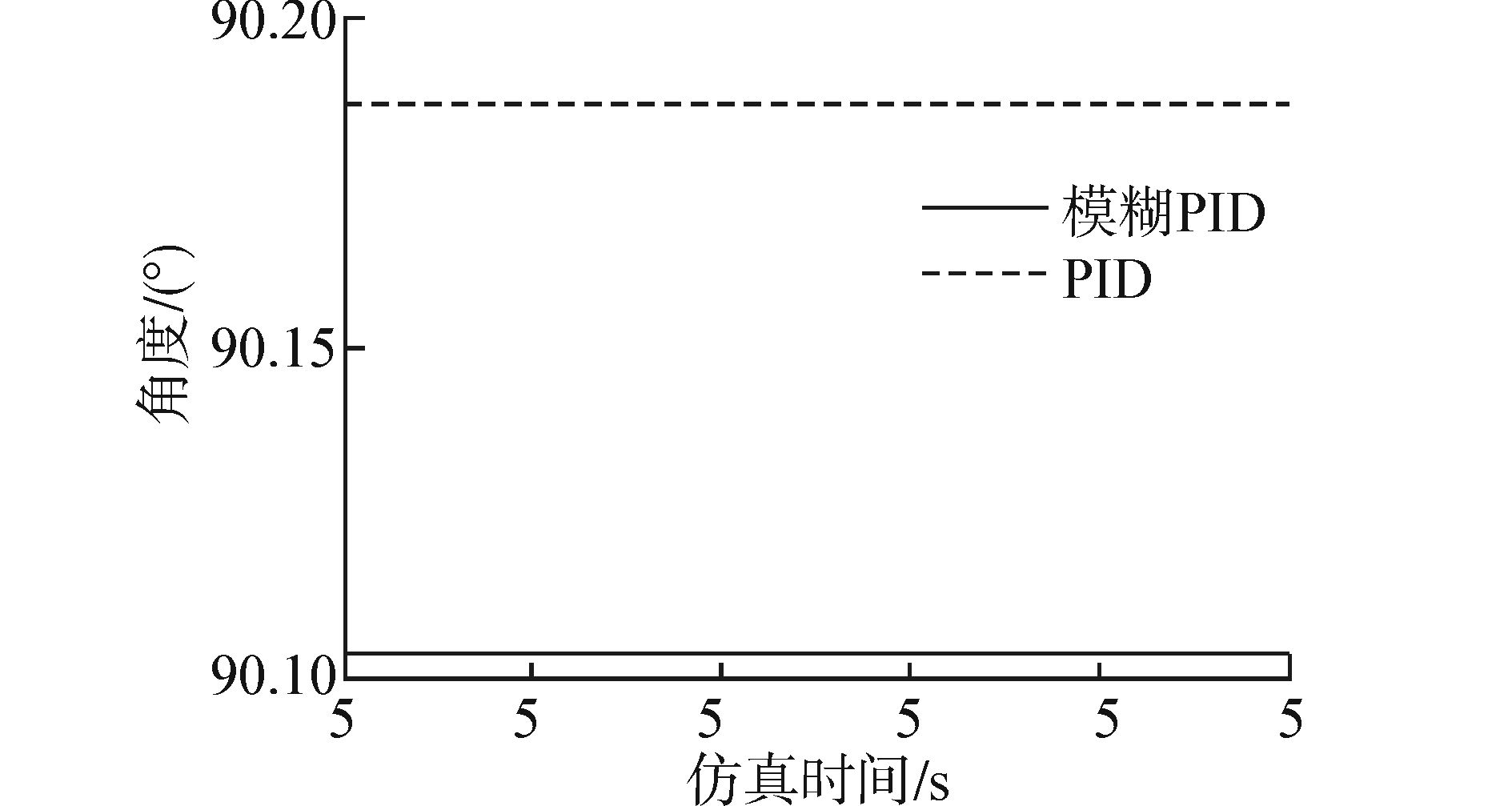
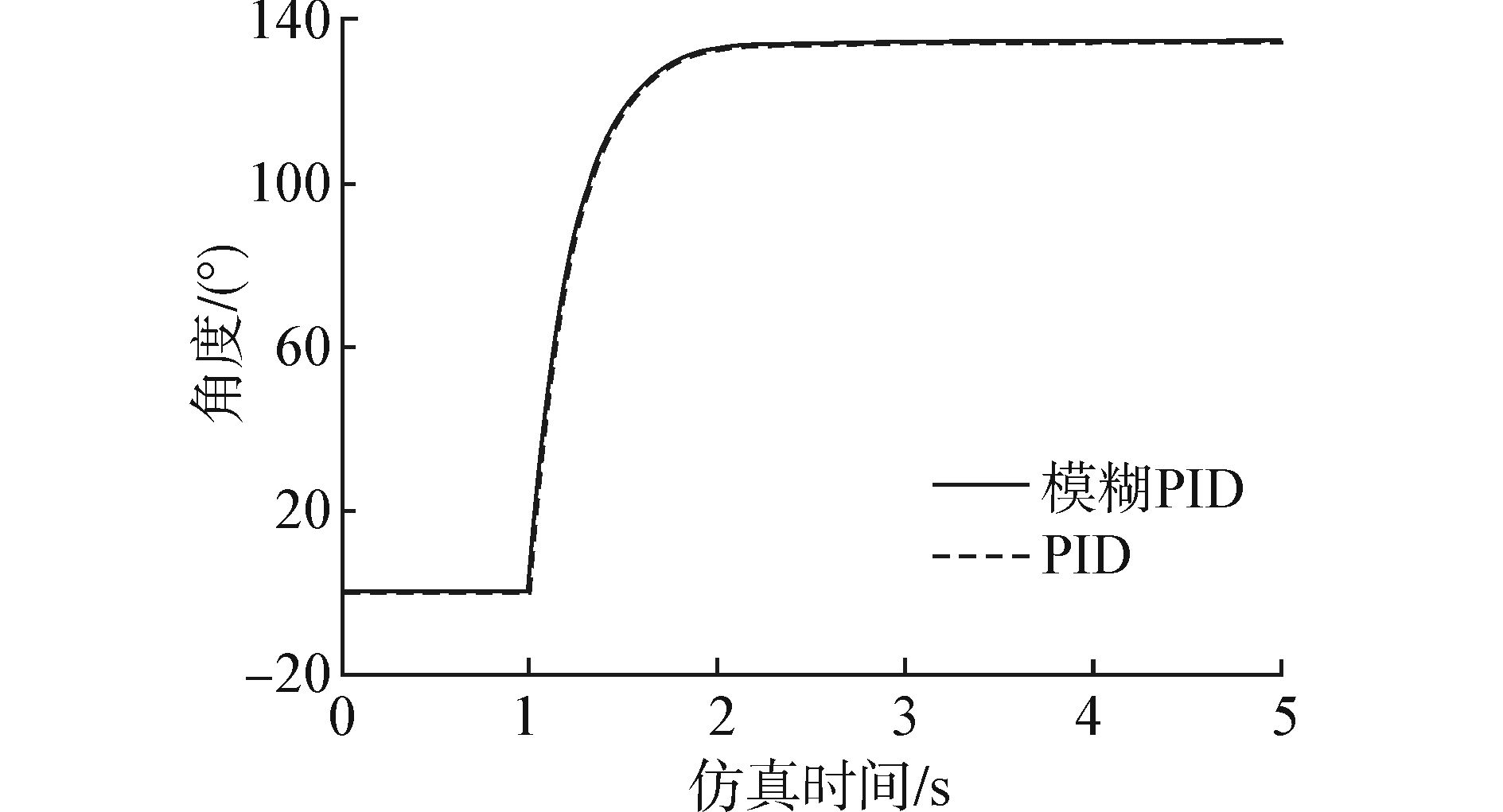
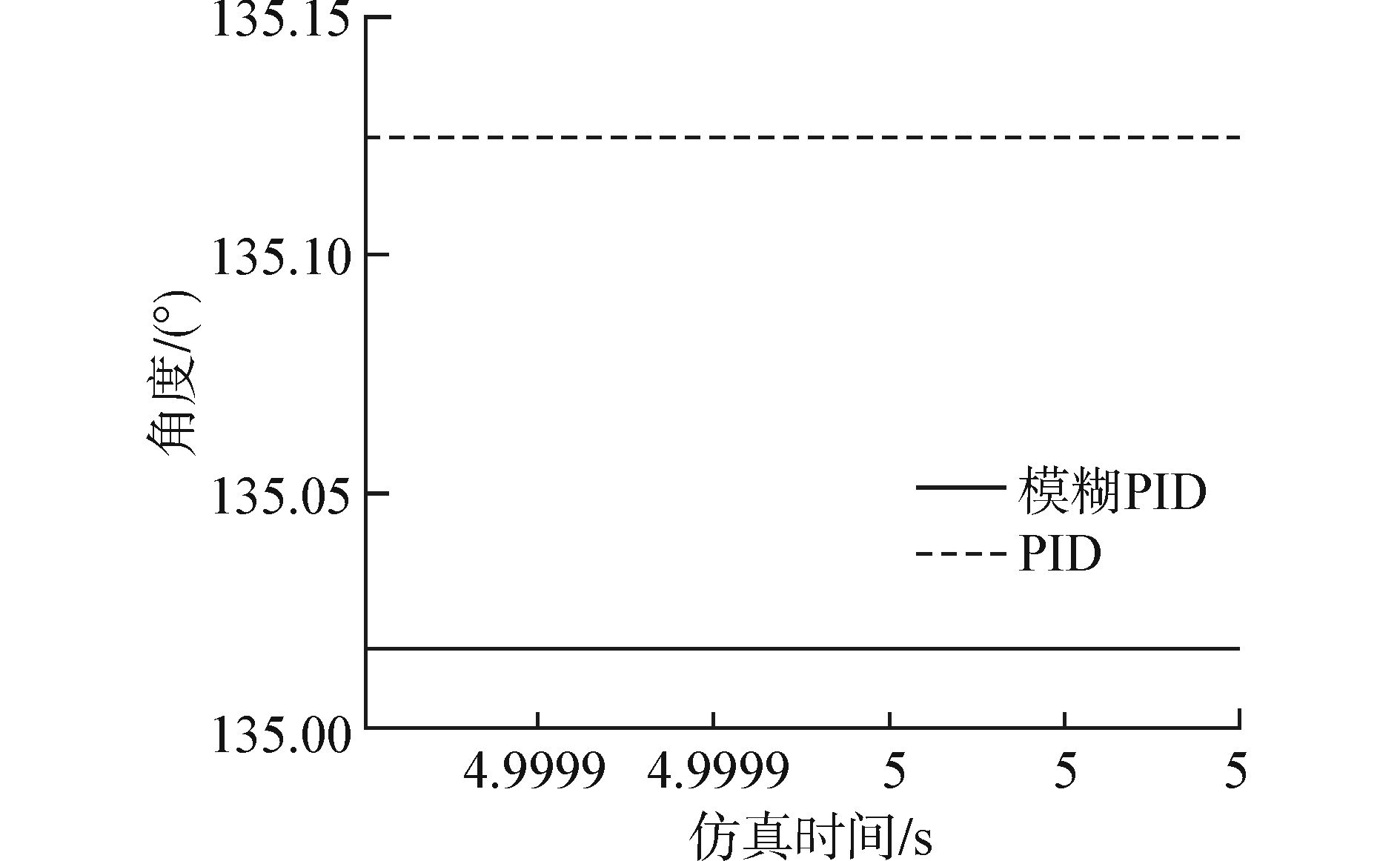
通过SimMechanics建立仿真模型,并利用模糊PID进行控制[17]。如图 12所示。启动仿真,调节模糊PID参数。从仿真曲线可以看到PID控制与模糊PID控制两者之间的差别。图 13为启动仿真后得到的第1根杆旋转角度的完整图,图 14为图 13的局部放大图。图 15为第2根杆旋转角度的完整图,图 16为图 15的局部放大图。从图 14和图 16两根杆旋转角度的局部放大图可以看到,模糊PID控制要比PID控制的定位更加精确。
|
| 图 12 第1、2根杆模糊PID模块 Fig. 12 Fuzzy PID block of the first and second arm |
|
| 图 13 第1根杆旋转角度完整图 Fig. 13 The complete graph of the first arm rotation angle |
|
| 图 14 第1根杆旋转角度局部放大图 Fig. 14 Partial enlarged drawing of the first arm rotation angle |
|
| 图 15 第2根杆旋转角度完整图 Fig. 15 The complete graph of the second arm rotation angle |
|
| 图 16 第2根杆旋转角度局部放大图 Fig. 16 Partial enlarged drawing of the second arm rotation angle |
通过对二连杆投球机器人运动学方程和动力学方程的推导,得到了二连杆投球机器人的动态数学模型,此建模过程简单、方便、有效,便于进行动力学分析和控制问题的研究。把得到的二连杆投球机器人的数学模型嵌入到MATLAB仿真中,得到二连杆机器人的运动情况,并在仿真过程中加入了PID模块和模糊PID模块,仿真结果得出模糊PID控制精确性更高。本设计仅对二连杆投球机器人进行了建模与仿真,下一步将对整体系统进行进一步的研究。
| [1] | 范永, 谭民. 机器人控制器的现状及展望[J]. 机器人, 1999(1): 75-80.FAN Yong, TAN Min. Current state and tendencies in the development of robot controller[J]. Robot, 1999(1): 75-80. |
| [2] | 张锐, 吴成东. 机器人智能控制研究进展[J]. 沈阳建筑工程学院学报:自然科学版, 2003, 11(1): 61-65.ZHANG Rui, WU Chengdong. Some recent progress in robotic intelligent control[J]. Journal of Shenyang Architectural and Civil Engineering Institute, 2003, 11(1): 61-65. |
| [3] | 蔡自兴, 陈海燕, 魏世勇. 智能控制工程研究的进展[J]. 控制工程, 2003, 10(1): 15-20.CAI Zixing, CHEN Haiyan, WEI Shiyong. Recent advances in research of intelligent control engineering[J]. Control Engineering of China, 2003, 10(1): 15-20. |
| [4] | 贾玉赞. 浅议智能机器人发展及应用[J]. 太原科技, 2003, 5(3): 20-26.JIA Yuzan. Development of intellectual robot and its application[J]. Taiyuan Science and Technology, 2003, 5(3): 20-26. |
| [5] | 吴向阳, 戴先中, 孟正大. 分布式机器人控制器体系结构的研究[J]. 东南大学学报:自然科学版, 2003, 33(Supl.): 200-204.WU Xiangyang, DAI Xianzhong, MENG Zhengda. Research on distributed architecture of robot controller[J]. Journal of Southeast University: Natural Science Edition, 2003, 33(Supl.): 200-204. |
| [6] | 谭宝成, 程智远, 牟云霞, 等. 移动机器人模糊控制系统的设计[J]. 西安工业大学学报, 2007, 27(4): 366-370.TAN Baocheng, CHENG Zhiyuan, MOU Yunxia, et al. Design of mobile robot control system based on fuzzy control[J]. Journal of Xi'an Technological University, 2007, 27(4): 366-370. |
| [7] | 李庆中, 顾伟康, 叶秀清, 等. 移动机器人模糊控制方法研究[J]. 仪器仪表学报, 2002, 23(5): 480-484.LI Qingzhong, GU Weikang, YE Xiuqing, et al. Study on fuzzy control method for mobile robots[J]. Chinese Journal of Scientific Instrument, 2002, 23(5): 480-484. |
| [8] | 李余庆, 刘继忠, 张华. 模糊控制在机器人超生避障系统的应用[J]. 机器人技术, 2009, 25(52): 216-218.LI Yuqing, LIU Jizhong, ZHANG Hua. Application of fuzzy control in ultrasound obstacle avoidance system for robot[J]. Robot Technology, 2009, 25(52): 216-218. |
| [9] | 樊晓平, 徐建闽. 柔性机器人的动力学建模及其仿真[J].控制理论与应用, 1997, 5(6): 60-69.FAN Xiaoping, XU Jianmin. Dynamic modeling and simulation of flexible robotic manipulators[J]. Control Theory and Applications, 1997, 5(6): 60-69. |
| [10] | 田永利, 邹慧君, 郭为忠, 等. 基于Matlab-Sim Mechanics的机电产品组成建模与仿真技术研究[J]. 机械设计与研究, 2002, 19(12): 10-12.TIAN Yongli, ZOU Huijun, GUO Weizhong, et al. Study on modeling and simulation methods for constitution objects of mechatronic products based on Matlab-Sim Mechanics[J]. Machine Design and Research, 2002, 19(12): 10-12. |
| [11] | 陆佑方, 冯冠民, 齐朝晖. 柔性机械臂动力学与控制建模的若干基本问题[J]. 机器人, 1993, 15(2): 52-59.LU Youfang, FENG Guanmin, QI Zhaohui. Application of artificial neural networks in dynamic identification and position control of robot manipulators[J]. Robot, 1993, 15(2): 52-59. |
| [12] | 吴宏鑫, 沈少萍. PID控制应用与理论依据[J]. 控制工程, 2003, 37(1): 6-10.WU Hongxin, SHEN Shaoping. Basis of theory and applications on PID control[J]. Control Engineering of China, 2003, 37(1): 6-10. |
| [13] | 陆磊. 模糊控制在轮式机器人上的应用[J]. 微型电脑应用, 2010, 26(12): 31-33.LU Lei. Application of fuzzy-PID controller in moble robot[J]. Microcomputer Applications, 2010, 26(12): 31-33. |
| [14] | 阎绍泽, 刘又午, 张铁民. 柔性机械臂动力特性的实验研究[J]. 河北工业大学学报, 1996, 25(11): 12-16.YAN Shaoze, LIU Youwu, ZHANG Tiemin. Experimental study on dynamic performances of flexible manipulators[J]. Journal of Hebei University of Technology, 1996, 25(11): 12-16. |
| [15] | 孙奎, 谢宗武, 刘宏. 一种新的机器人动力学仿真分析方法[J]. 机械设计与制造, 2008, 5(9): 163-165.SUN Kui, XIE Zongwu, LIU Hong. The dynamics simulation analysis of a four DOF manipulator [J]. Machinery Design & Manufacture, 2008, 5(9): 163-165. |
| [16] | The Mathworks Inc. SimMechanics user's guide[M]. Natick, USA: The Mathworks Inc., 2002: 22-27. |
| [17] | 苗敬利. 模糊控制和传统PID控制的仿真研究[J]. 微软计算机信息, 2003, 4(7): 18-24.MIAO Jingli. The simulation study between fuzzy control and PID control[J]. Microcomputer Information, 2003, 4(7): 18-24. |



