目前轨迹规划主要从2个方面进行优化,一是对时间的优化;二是对系统能量的优化;其中对最优时间的研究最多。机器人时间最优轨迹规划是指在满足各种约束条件下,以机器人运动时间最短为目标来规划机器人的运动轨迹[1]。对轨迹规划的时间最优,一般从2个方面考虑,一是以速度和加速度为约束条件;二是以运动学或动力学为约束,采用各种非线性约束的最优化算法实现机器人最优轨迹规划[2]。文献[3]以机器人的位置、速度、加速度和二阶加速度的运动学约束为前提,路径点之间用高次多项式作曲线轨迹,采用柔性多面体搜索的算法求解最优时间。由于在连接点处引入某一确定的加速度值使得抑制振动变得十分困难。为了避免机械手振动,延长关节使用寿命,关节轨迹都采用二次多项式加余弦函数的形式[4],不仅可以保证各关节运动的位移、速度、加速度连续,而且还可以保证各关节运动的二阶加速度连续。但是采用二次多项式加余弦函数的形式增加了计算的复杂度,需要耗费大量的计算时间。利用具有光滑特性的三次样条曲线段来连接路径点是最简单的多项式方法,在速度和加速度的约束下能够减小两点之间的运行时间,同时避免振荡[5]。基于多项式插值的轨迹规划,具有阶次高、没有凸包性质等特点,很难用传统方法优化[6]。文献[7]采用遗传算法对关节空间中各关键点间的运行时间间隔进行规划。但是遗传算法需要进行编码、解码过程,操作复杂。粒子群优化方法具有算法简单、参数设置少、实现简单,能够有效解决真实世界的复杂优化问题,与其他求解约束优化问题的方法相比有一定的优势[8]。文献[9, 10]采用粒子群优化算法对关节角轨迹进行时间最优化求解。
不同于以往对速度的单一限制,本文采用粒子群算法对任意关节速度下的机械臂进行运行时间的优化。
1 多项式插值函数的构造已知机器人在笛卡尔坐标系下起始点,2个路径点以及终点的空间坐标,通过逆运动学求解得到各个关节在4个插值点处的关节角度,用θij表示关节i插值的角度,其中i=1,2,…,n,n表示关节个数,j=1,2,3,4代表 4个插值点的序号。点与点之间采用3-5-3多项式插值的曲线轨迹。其约束条件是:已知第i个关节各段的初始点θi0、路径点θi1和θi2、末端点θi3,路径点之间的位置、速度与加速度连续以及初始点和终点的速度、加速度均为0。
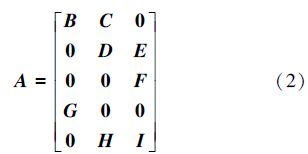
第i段关节3-5-3样条多项式的通式为
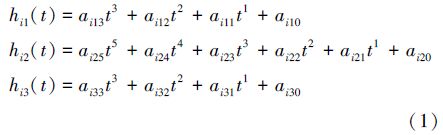
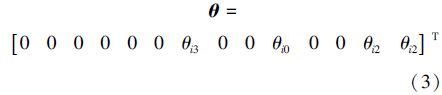

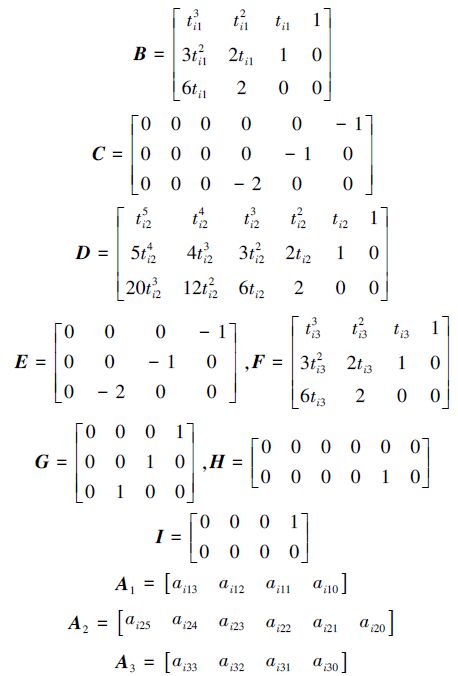
粒子群算法是一种基于群体智能的全局进化优化算法,它源于对鸟类捕食行为的模拟,将每个个体看作D维搜索空间中一个没有体积和质量的微粒[11, 12],且在搜索空间中以一定的速度飞行,通过群体中粒子之间的合作和竞争来寻找最优解。假设一个包含m个微粒的微粒群在其D维搜索空间中飞行,第i个粒子在D维空间的位置为xi=(xi1,xi2,…,xiD),飞行速度为vi=(vi1,vi2,…,viD),每个粒子都具有一个由被优化的目标函数决定的适应值,微粒i所经历的最好位置pg。对每一次迭代,第i个粒子的第d维分量(t1≤d≤D)在第k+1次迭代时的速度和位置按式(5)和(6)变化:
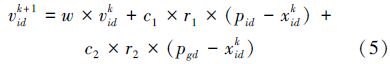
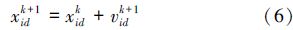
如果选择多项式的系数aij作为待寻优量,则根据式(2)~(4)可以得到时间变量ti1、ti2、ti3,这时候粒子群的维数为14维。如果直接选择在时间变量ti1、ti2、ti3的搜索空间进行优化,可以将维数降低,大大减少了粒子群寻优的复杂性和困难性。优化目标是使各个关节在约束的速度范围内以最短的时间运行。其适应度函数为
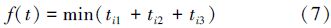
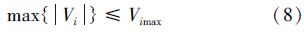
粒子群算法对机器人第i个关节进行最优时间轨迹规划,具体步骤如下:
1)选定种群的规模m(一般为20),在插值时间的3维搜索空间中随机产生m个粒子构成初始种群,并初始化粒子的位置和速度。
2)由m组时间变量ti1、ti2、ti3代入式(2)~(4)中可得出3-5-3多项式的未知系数aij。
3)将3-5-3多项式的系数aij代入式(1)并对时间求导,得到关节角度的速度函数,判断实时速度是在否满足式(8)。
4)计算每个微粒的适应度值。对步骤3)的计算结果进行筛选,如果3段中的任何一段速度不符合式(8),则将该粒子的适应度值设置为极大的常数,在寻找最优粒子时,通过适应度值的比较,将会排除这个适应度值较大的粒子,不被筛选为最优粒子。而这个粒子本身也会慢慢向最佳值进行靠拢,直到满足速度的约束。如果3段的最大速度都符合式(8),则采用式(7)作为适应度函数,粒子群算法迭代以获得最小插值时间为目标。
5)对每个微粒,将其适应度值与其经历过的最好位置pi的适应度值作比较,如果较好,则将其替换为当前的最好位置pi。
6)比较每个微粒当前最好位置的适应度值,得到当前整体最优粒子,再与群体所经历的全局最好位置pg作比较,如果较好,则替换pg。
7)根据式(5)~(6)变化微粒的速度和位置,重新整合成新的由m个粒子构成的种群。
8)如满足终止条件(通常为足够好的适应值或达到一个预设最大迭代次数(Nmax)则算法结束,否则返回步骤2)。
本文设定粒子群的个数m为20,初始的粒子位置为[0.1,4.0]的任意随机数,粒子的最大飞行速度在[-2,2]之间。粒子飞行速度的参数设置为惯性权重w=(Wmax-i×(Wmax-Wmin)/Nmax),Wmax=0.9,Wmin=0.4,i为迭代次数,循环迭代步数Nmax为50。权重因子c1=2,c2=2,r1和r2为[0,1]的随机数。
3 机器人建模与PSO仿真本文主要研究工业机器人六自由度机械臂,采用标准D-H坐标系法进行运动学建模[14],如图 1所示。6个关节的D-H参数见表 1。
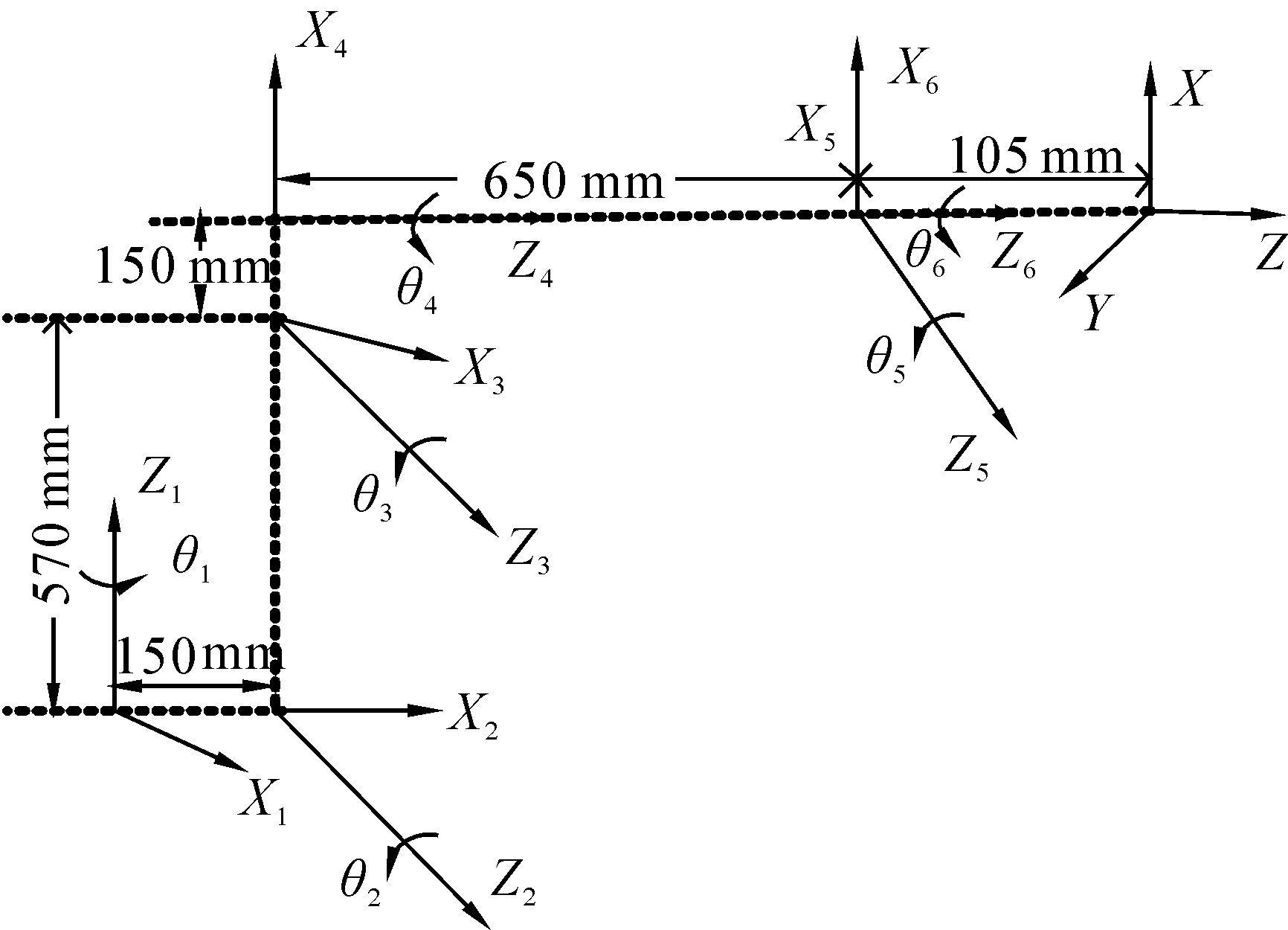
|
| 图 1 机械臂的D-H坐标系 Fig. 1 The D-H coordinates of robot manipulators |
| 关节i | di/mm | ai/mm | ai/(°) | θi/(°) | 关节变量范围/(°) |
| 1 | 0 | 150 | 90 | 0 | [-150,150] |
| 2 | 0 | 570 | 0 | 90 | [-80,65] |
| 3 | 0 | 150 | 90 | 0 | [-80,80 |
| 4 | 650 | 0 | -90 | 0 | [-175,175] |
| 5 | 0 | 0 | 90 | 0 | [-110, 110] |
| 6 | 0 | 105 | 0 | 0 | [-200, 200] |
通过解析法用4×4的齐次变换矩阵可以求解出机械臂位置控制和方向控制的各关节角度的逆运动学解析解。在直角坐标系下给定机械臂末端的轨迹插值点,如表 2。由逆运动学将各空间笛卡尔位置插值点转化为关节空间的角度插值点。
| 起始点 | 路径点1 | 路径点2 | 终点 |
| (800,0,615) | (950,100,560) | (750,300,560) | (550,200,700) |
通过逆运动学解,得到1~6关节的初始位置,路径点和终点所对应的角度如表 3所示。
| 关节i | θj0 | θj1 | θj2 | θj3 |
| 关节1 | 0 | -6.009 | -21.803 | -19.983 |
| 关节2 | 0 | 15.053 | -0.851 | -18.161 |
| 关节3 | 0 | 11.948 | -10.833 | -7.900 |
| 关节4 | 0 | 0 | 0 | 0 |
| 关节5 | 90 | 86.871 | 79.975 | 100.240 |
| 关节6 | 0 | -6.009 | -21.803 | -19.983 |
按照第2节中的方法,在不同速度约束下,关节1采用PSO求解最优时间,跟踪群体最好位置pg在每次迭代过程中的位置变化,得到关节1的最优粒子pg位置进化图,如图 2。可以看出,在不同速度约束下,关节1最优粒子pg最多经过30次迭代就快速收敛。其各个收敛值即为在特定的速度约束之下,关节1运行三段插值多项式所需要的最短时间为t11、t12和t13,如表 4所示。
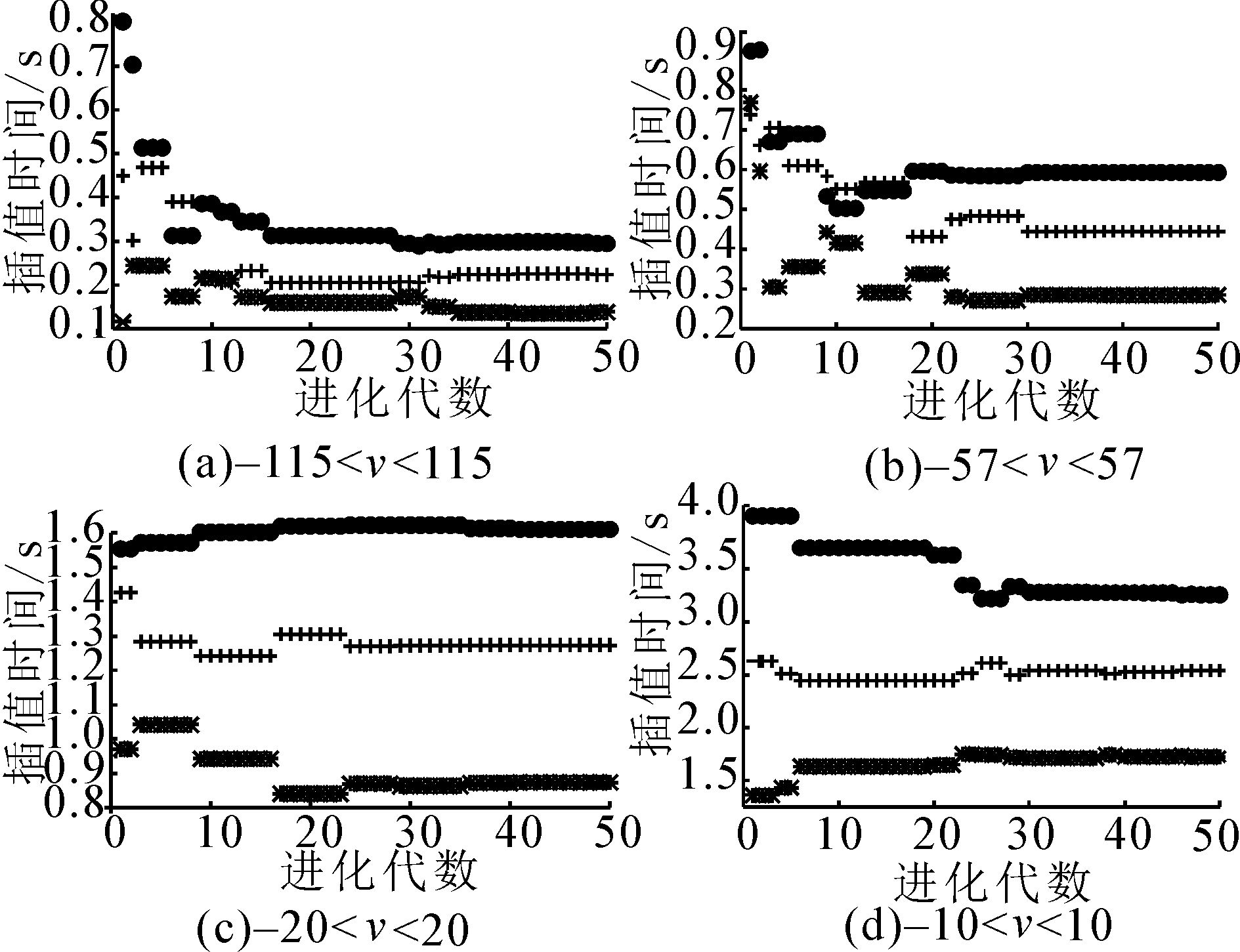
|
| 图 2 关节1的最优粒子pg位置进化 Fig. 2 The optimal particle pgof joints 1 evolution |
| 速度范围(°/s) | t11/s | t12/s | t13/s |
| (-115,115) | 0.222 9 | 0.294 9 | 0.138 4 |
| (-57,57) | 0.444 9 | 0.592 4 | 0.285 6 |
| (-20,20) | 1.274 7 | 1.636 1 | 0.848 5 |
| (-10,10) | 2.567 1 | 3.245 8 | 1.720 9 |
对于其他关节也同样采用上述方法进行寻优,从而得到各个关节在不同速度约束下的运行最优时间。由于研究目标是大型的工业机器人,关节速度不宜采取过大,否则会产生强烈的振动,不利于机器人长期、高效、稳定的运行。所以取关节速度在[-20,20](°/s)为例,按照与关节1同样的优化方法,得到各个关节的最短插值时间,如表 5。从表中可以看出,第4关节的位置与机器人的姿态完全相关,因为机器人姿态在运动过程中始终保持不变,所以关节4的位置也没有发生变化,插值时间和速度都为0。关节1和关节6的运动状态完全重合。
| 关节i | ti1/s | ti2/s | ti3/s |
| 关节1 | 1.274 7 | 1.636 1 | 0.848 5 |
| 关节2 | 3.116 2 | 2.188 8 | 3.280 0 |
| 关节3 | 3.107 0 | 3.997 7 | 1.605 0 |
| 关节4 | 0 | 0 | 0 |
| 关节5 | 0.813 1 | 1.170 2 | 3.062 0 |
| 关节6 | 1.274 7 | 1.636 1 | 0.848 5 |
由于机器人各个关节是在同一时间内运动,所以每段插值时间取各关节该段插值时间的最大值,t1=max{ti1},t2=max{ti2},t3=max{ti3}(i=1,2,…,6)。则t1=3.116 2,t2=3.997 7,t3=3.280 0。
通过离线优化得到最短的插值时间,在机器人控制平台上编程实现3-5-3多项式时间最优轨迹规划,并进行实验。图 3~图 5分别是各关节的位置、速度、加速度的实验曲线。从图中可以看出关节位置,速度,加速度均满足14个运动学约束条件。图 4中,各个关节速度的最大值和最小值都在第2段插值时出现,第2关节和第3关节的速度在第2段时趋近于t-Vmax,第5关节的速度在第2段时趋近于tVmax。

|
| 图 3 粒子群优化的机械臂关节位置曲线 Fig. 3 Mechanical arms’ joint position curves of PSO |
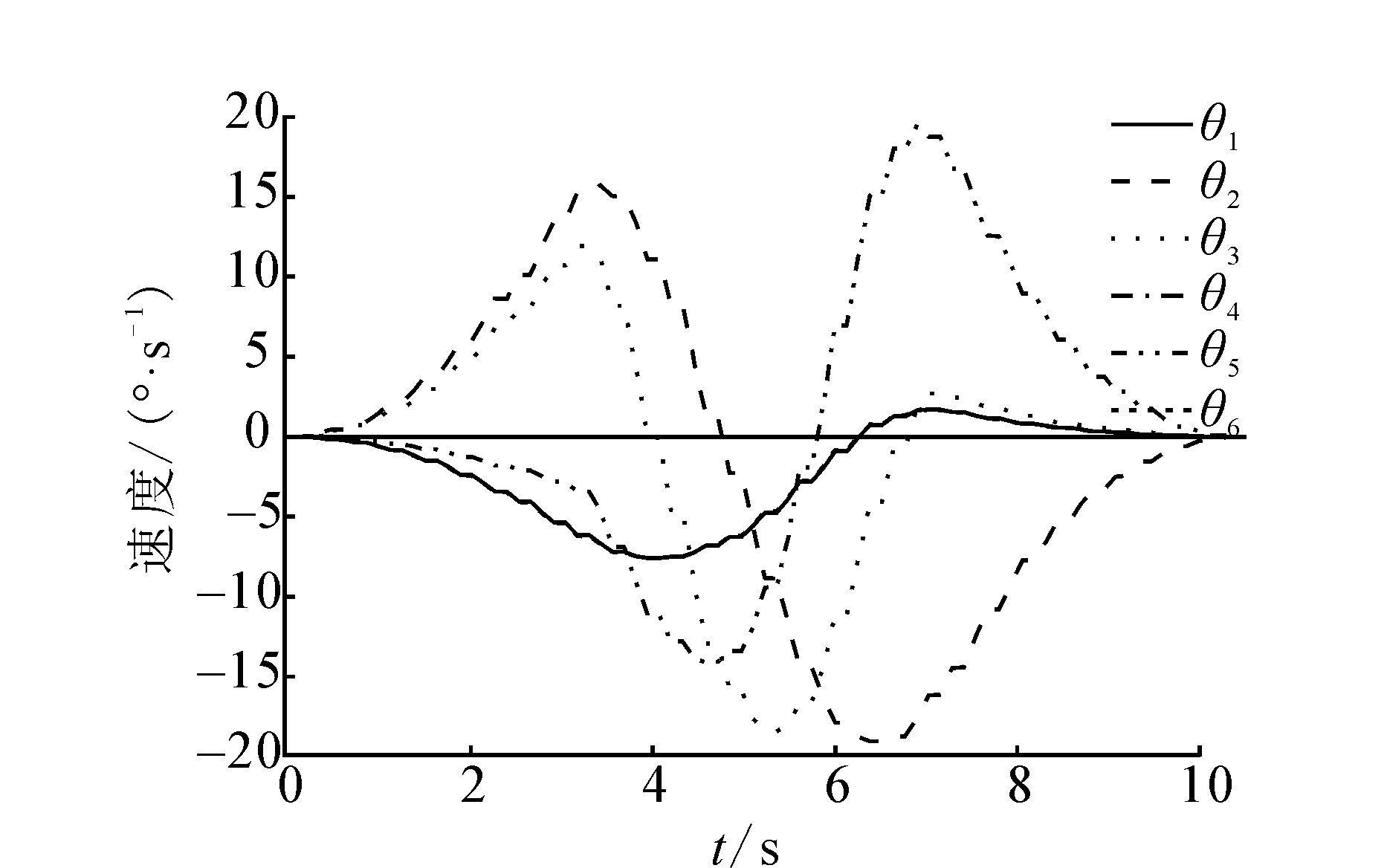
|
| 图 4 粒子群优化的机械臂关节速度曲线 Fig. 4 Mechanical arms’ joint speed curves of PSO |
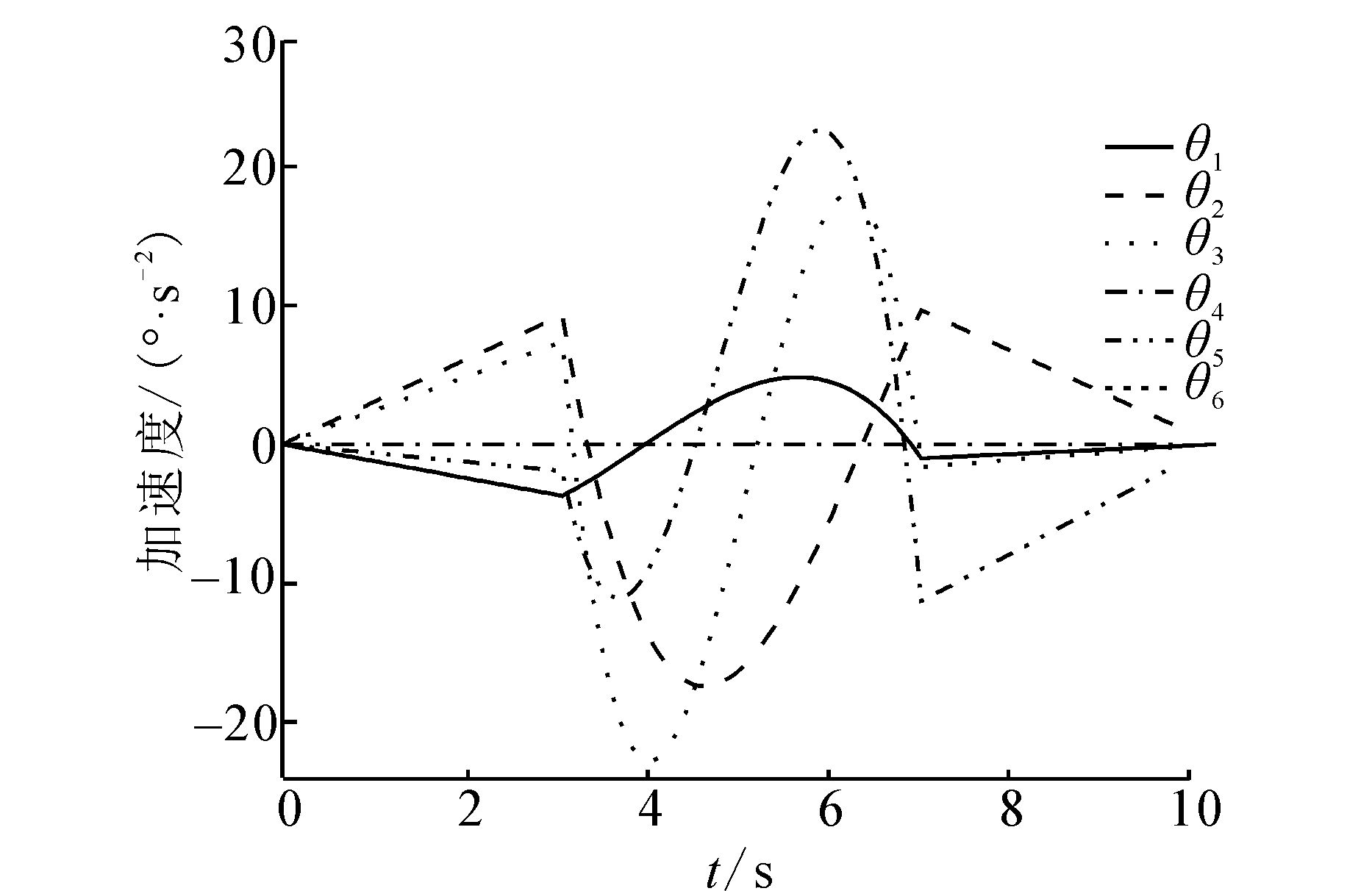
|
| 图 5 粒子群优化的机械臂关节加速度曲线 Fig. 5 Mechanical arms’ joint acceleration curves of PSO |
图 6是粒子群优化的机械臂关节脉动曲线,由于3-5-3多项式3次导数只有在某些特殊的情况下才能保持连续。机械手的轨迹精度和关节脉动有密切关系,关节脉动越小则机械手的轨迹精度越高[15]。此时,机械手的轨迹精度较低,误差较大,同时使用寿命也会减少。如果要使脉动连续,则要以提高阶次或复杂度为代价。在采集关节角度数据的同时采集机器人的实时空间坐标,图 7是在基于粒子群优化的机械臂笛卡尔坐标下三维立体实验轨迹曲线。可以看出曲线经过预设的点。实验验证了速度约束下的PSO六自由度机械臂多项式插值轨迹规化的有效性。
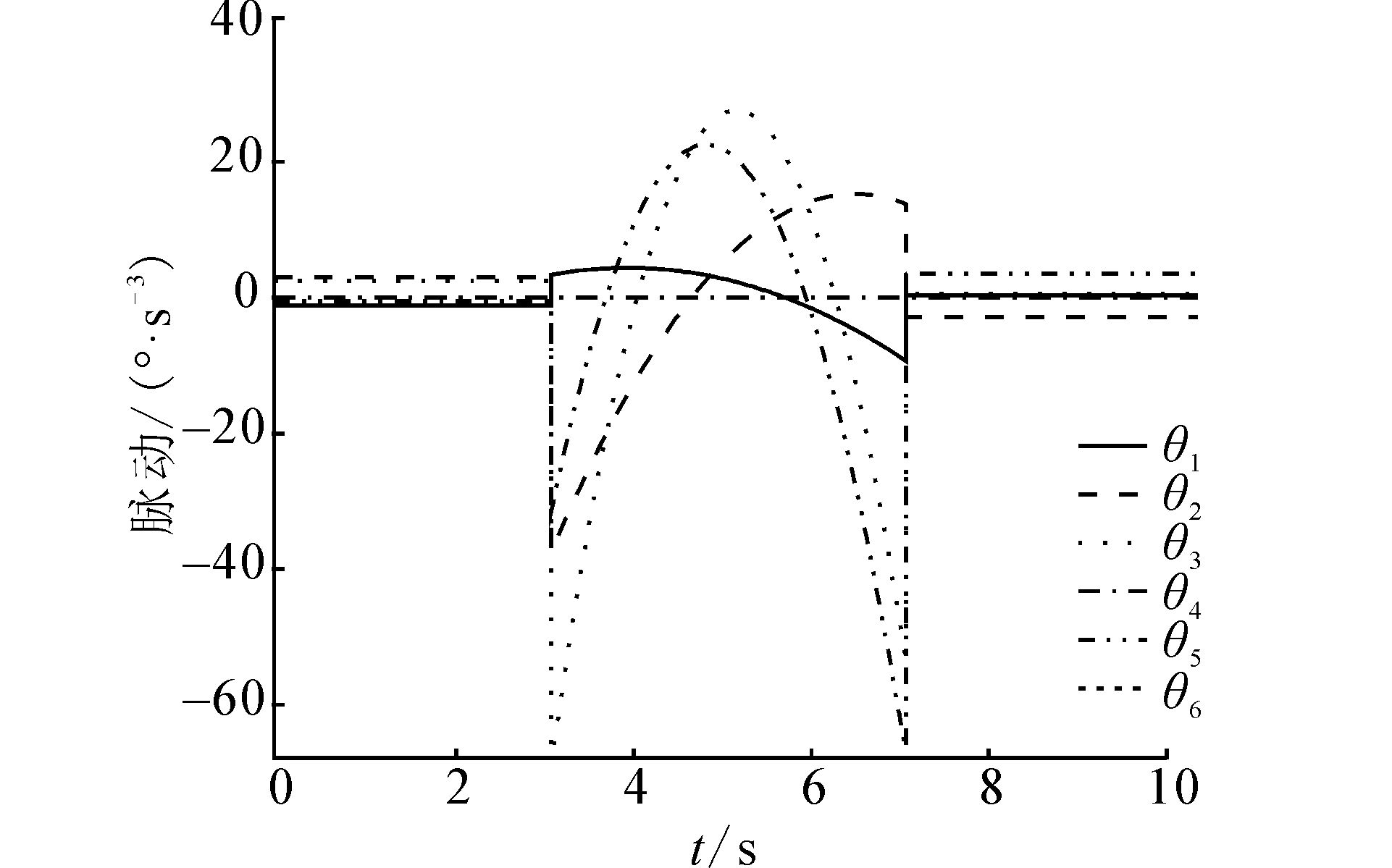
|
| 图 6 粒子群优化的机械臂关节脉动曲线 Fig. 6 Mechanical arms’ joint pulsation curves of PSO |
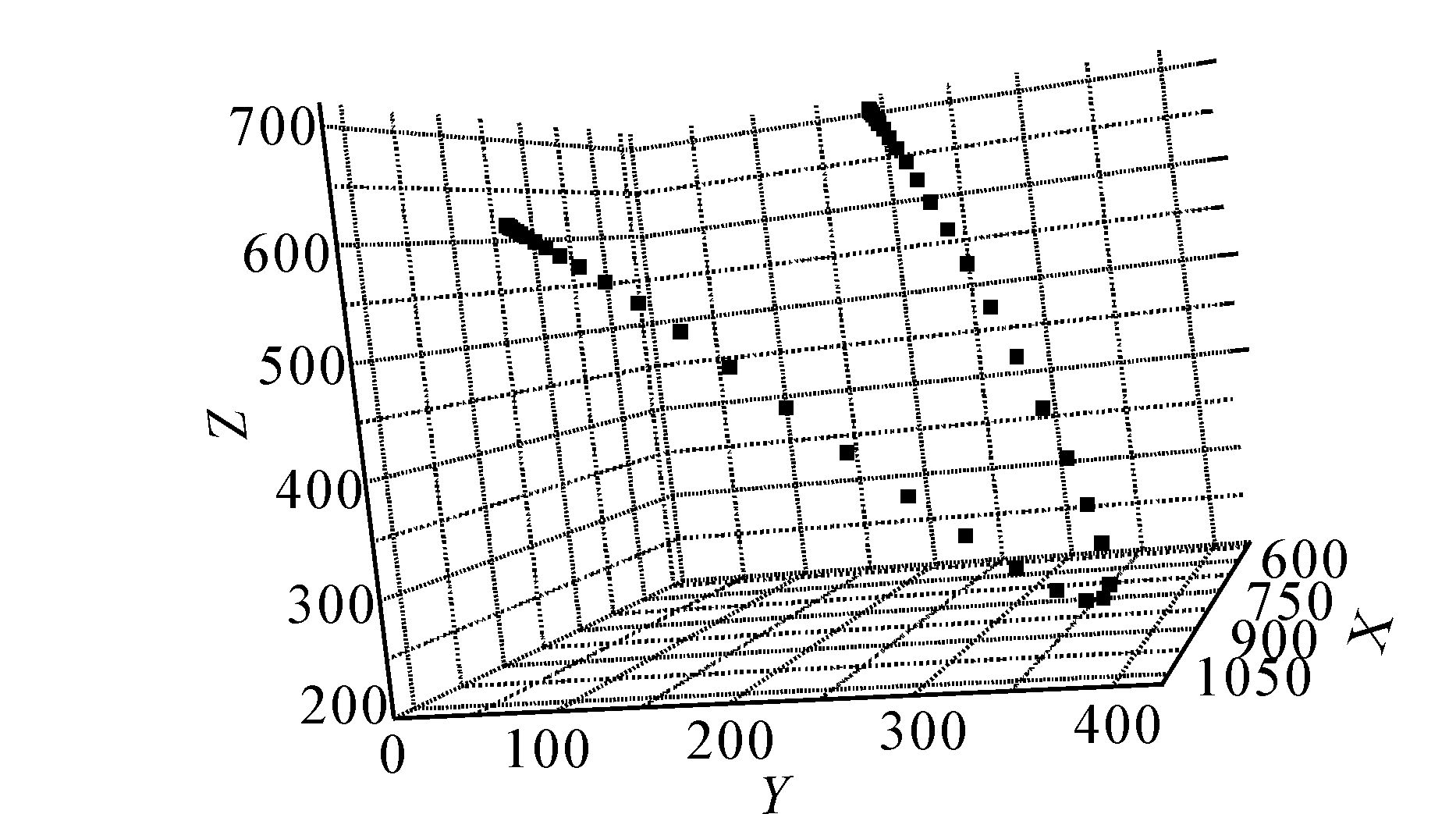
|
| 图 7 基于粒子群优化的机械臂轨迹曲线 Fig. 7 Mechanical arms’ joint trajectory curve of PSO |
采用速度约束下的PSO算法在计算机上离线寻优出机器人3段插值最优时间,在机器人控制平台上进行编程实验,实验结果证明了速度约束下的PSO六自由度机械臂时间最优轨迹规划的可靠性。
传统3-5-3多项式插值,没有确定各段插值时间的准则,插值时间是随便选取的已知数。根据14个已知条件,求出各个关节在3段插值时间内的多项式,对于3-5-3多项式求导得到速度函数2-4-2多项式,要求各个关节的速度满足一定的约束条件,即要使这些多项式的值在约束范围内,要求高次多项式满足限定条件,这本身就是非常复杂的数学问题,加之多项式的系数本身就与插值时间有关,在满足速度约束的条件下同时还要进行时间最优,就更是一个复杂的难题,难以用传统的方法解决。而粒子群算法能有效地解决这种复杂的约束优化问题。
在计算式(2)时,由于粒子群中的每个粒子都是随机产生的,可能造成矩阵不满秩,不利于矩阵求逆。但是对寻优过程并不会有太大影响,如果矩阵不满秩,求解式(4)时使得a的各个系数为无穷大,在后续粒子群寻优过程中,这个粒子会不满足速度的约束条件从而被筛选出来。
本文在研究过程中并没有考虑脉动不连续对机器人造成的不利影响,下一步的工作就是在分析脉动对系统的作用基础之上考虑脉动不连续的解决方案。
| [1] | 李达. 工业机器人轨迹规划控制系统的研究[D]. 哈尔滨: 哈尔滨工业大学, 2011: 2-3.LI Da. Study on industrial robot control system of trajectory planning[D]. Harbin, China: Harbin Institute of Technology, 2011: 2-3. |
| [2] | 张红强. 工业机器人时间最优轨迹规划[D]. 长沙: 湖南大学, 2004: 9-10.ZHANG Hongqiang. Time-optimal trajectory planning of industrial robot[D]. Changsha, China: Hunan University, 2004: 9-10. |
| [3] | LIN C S, CHANG P R, LUH J Y S. Formulation and optimization of cubic polynomial joint trajectories for industrial robots[J]. IEEE Transactions on Automatic Control, 1983, 28(12): 1066-1074. |
| [4] | 谭冠政, 王越超. 工业机器人时间最优轨迹规划及轨迹控制的理论与实验研究[J]. 控制理论与应用, 2003, 20(2): 185-192.TAN Guanzheng, WANG Yuechao. Theoretical and experimental research on time-optimal trajectory planning and control of industrial robots[J]. Control Theory & Applications, 2003, 20(2): 185-192. |
| [5] | BAZAZ S A, TONDU B. Minimum time on-line joint trajectory generator based on low order spline method for industrial manipulators[J]. Robotics and Autonomous Systems, 1999, 29(4): 257-268. |
| [6] | 付荣, 居鹤华. 基于粒子群优化的时间最优机械臂轨迹规划算法[J]. 信息与控制, 2011, 40(6): 802-808.FU Rong, JU Hehua. Time-optimal trajectory planning algorithm for manipulator based on PSO[J]. Information and Control, 2011, 40(6): 802-808. |
| [7] | 李东洁, 邱江艳, 尤波. 一种机器人轨迹规划的优化算法[J]. 电机与控制学报, 2009, 13(1): 123-127.LI Dongjie, QIU Jiangyan, YOU Bo. Optimal algorithm for trajectory planning of the robot[J]. Electric Machines and Control, 2009, 13(1): 123-127. |
| [8] | LI Yanliang, SHAO Wei, YOU Long, et al. An improved PSO algorithm and its application to UWB antenna design[J]. IEEE Antennas and Wireless Propagation Letters, 2013, 12: 1236-1239. |
| [9] | GUO Tongying, LI Feng, HUANG Kuan, et al. Application of optimal algorithm on trajectory planning of mechanical arm based on B-Spline curve[J]. Applied Mechanics and Materials, 2013, 376: 253-256. |
| [10] | SASKA M, MACAS M, PREUCIL L, et al. Robot path planning using particle swarm optimization of Ferguson splines[C]//IEEE Conference on Emerging Technologies and Factory Automation. Prague, Czech Republic, 2006: 833-839. |
| [11] | 谢晓锋, 张文俊, 杨之廉. 微粒群算法综述[J]. 控制与决策, 2003, 18(2): 129-134.XIE Xiaofeng, ZHANG Wenjun, YANG Zhilian. Overview of particle swarm optimization[J]. Control and Decision, 2003, 18(2): 129-134. |
| [12] | SUPAKAR N, SENTIHIL A. PSO obstacle avoidance algorithm for robot in unknown environment[C]//International Conference on Communication and Computer Vision (ICCCV). Coimbatore, India, 2013: 1-7. |
| [13] | HU Menqi, WU T, WEIR J D. An adaptive particle swarm optimization with multiple adaptive methods[J]. IEEE Transactions on Evolutionary computation, 2013, 17(5): 705-720. |
| [14] | 尼库拉 库克. 机器人学导论—分析、控制及应用[M]. 孙富春, 朱纪洪, 刘国栋等, 译. 第4版. 北京: 电子工业出版社, 2004: 60-72. |
| [15] | BORYGA M, GRABOS A. Planning of manipulator motion trajectory with higher-degree polynomials use[J]. Mechanism and Machine Theory, 2009, 44(7): 1400-1419. |



