粒子滤波(particle filter,PF)[1,2]是一种基于蒙特卡罗思想的非线性、非高斯系统滤波方法,对系统的过程噪声和量测噪声没有任何限制。PF跟踪算法相对于规则穷举搜索算法,缩小了采样区域,且与跟踪目标大小无关,可以迭代持续进行,而不是简单地只按固定比例扩大目标周围的搜索区域,因而被广泛应用于目标跟踪领域[3,4,5]。然而,基于PF算法的视频运动目标跟踪过程中,目标发生形变或严重遮挡以及背景和光照变化的干扰等都极易造成目标跟踪发生偏移甚至丢失目标。因此,近年来许多学者针对复杂情况下PF滤波算法如何精确、快速、稳定地跟踪视频运动目标进行了深入研究并加以改进。例如:文献[4]提出基于稀疏估计的PF算法,将跟踪目标稀疏表示为目标、非负和负模板子集形式,根据投影差值最小的目标特征找到最优跟踪状态估计,并动态更新目标模板以适应复杂情况下的目标变化,达到很好的跟踪效果。文献[6]针对复杂场景提出基于目标颜色特征的自适应PF算法,该算法自适应选择粒子数量和高斯噪声的方差,可以有效克服目标形变、光照变化的影响,保证跟踪的实时性和粒子的有效性。文献[7]提出分块模板更新算法,改善了整体模板更新算法丢失目标空间信息的缺点,有效防止了模板漂移,并能较好地适应目标的外观变化,具有较强的抗遮挡能力。文献[8]提出的基SIFT特征的PF算法,以目标颜色投影和成像角度为分块标准自适应分块,并自适应更新目标模型的SIFT特征点适应目标外观变化,采用最小二乘法对目标状态进行校准,保证了跟踪结果的精度。文献[9]提出了自适应不完全的重采样方法(particle filter based on adaptive part resampling,APRPF),能根据当前滤波步粒子的退化程度自适应地选择参与重采样粒子的数目,重采样后的新生粒子缓解退化问题,未参与重采样的粒子保持了粒子集的多样性,不仅提高了滤波精度,还减少了计算量。但是,上述改进算法的收敛速度和估计误差由于仍然依赖PF算法本身的迭代过程,因而存在局限性。当背景发生突变,目标模板更新不及时容易造成目标跟踪发生偏移甚至丢失目标。因此,本文提出基于元认知模型的粒子滤波算法(metacognitive particle filter,MCPF),该算法不依赖于PF算法本身迭代过程,能够对目标模板进行认知,及时监控到突变,控制并调节MCPF决策机制,实现目标跟踪。
1 元认知哲学家Alfred Tarski于1956年引进“元”(meta)概念之后,元认知(metacognition)概念最早由美国心理学家J. H. Flavell在心理学领域提出[10]。按照“元”概念的哲学思考,元认知即是认知的认知,目前已经成为认知心理学和教育心理学的一个重要领域和研究热点。近年来,国内外元认知研究主要来自于教育心理学研究的驱动,元认知在教育心理学领域里具有重要实践意义[11,12,13,14,15]。文献[11]提出元认知的实质就是人对认知活动的自我意识和自我调节,R. J. Sternberg提出的新的智力模式中已反映元认知在认知活动中所起的支配地位,在任何一项认知活动中的元认知培养训练效果都具有广泛的迁移性,并整合了J. H. Flavell和A. Brown的观点,将元认知分为元认知知识(metacognitive knowledge,MK)、元认知体验(metacognitive experience,ME)和元认知监控(metacognitive regulation,MR),这种思想影响广泛,被国内外大部分学者所认同。文献[12]提出元认知知识为改进学习提供反馈信息,元认知体验调节和促进学习活动,监控提高学习效率的重要心理因素,培养和发展元认知能力有助于学习水平的提高,并展现了解决学习问题的一个模式图。
受上述元认知理论启发,本文将目标跟踪作为认知活动,构建了具有元认知能力的MCPF目标跟踪算法。首先,MCPF对初始化目标模板进行认知,建立目标认知模板(object cognitive model,OCM)和背景认知模板(background cognitive model,BCM)作为MCPF的认知知识成分(metacognitive knowledge,MK),然后,MCPF监控(metacognitive regulation,MR)多次迭代后采样粒子的观测信息,刺激产生MCPF元认知体验成分(metacognitive experience,ME),并根据元认知体验成分有效地调节MCPF算法的决策机制,实现稳定的目标跟踪。
2 元认知粒子滤波模型 2.1 MCPF模型定义本文提出的元认知粒子滤波模型包括MCPF认知知识成分(MCPF-K)、MCPF体验成分(MCPF-E)和MCPF监控成分(MCPF-R)3个成分。简单描述三部分的功能:一方面,以MCPF-K为基础,MCPF-R受到MCPF-E的激发和指引;另一方面,MCPF-R不断刺激新的MCPF-E产生,同时也会发展MCPF-K,并且MCPF-K可以形成新意识发展为MCPF-E,MCPF-E刺激新的MCPF-K产生。这3个方面相互作用、循环往复,三者动态有机的结合即构成了MCPF模型(如图 1所示)。
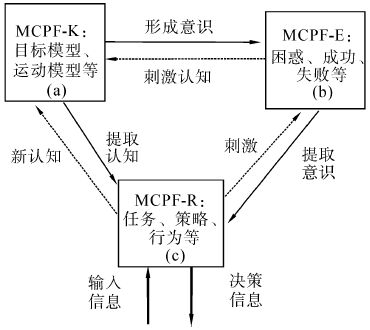
|
| 图 1 MCPF模型 Fig. 1 MCPF Model |
MCPF每个成分和行为的定义描述如下:
定义1 MCPF认知知识成分(MCPF-K) 元认知的MK成分是有关认知活动系统的知识。MCPF-K包括粒子集合的运动模型(motion model,MM)、 目标模型(object model,OM)、目标认知模型(OCM)和背景认知模型(BCM)以及由MCPF-E和MCPF-R发展的新认知知识。即 KMCPF={IiOM,IiOCM,IiBCM,Ml},i=1,2,...,l=1,2,...
如图 1(a)所示。MCPF-K中的IiOM,IiOCM,IiBCM,Ml目标特征可以选用目标颜色特征[6]、分块模型[7,16]、SIFT特征[8]等。
定义2 MCPF体验成分(MCPF-E) 元认知的ME是伴随有关认知活动而产生的认知体验与情感体验。MCPF-E包括采样粒子的观测图像特征与当前目标模板或认知粒子模板匹配成功(true,T)、失败(fail,F)或困惑(puzzled,P)的意识,即EMCPF={T,F,P};MCPF-E接收来自MCPF-K的新意识e,并刺激发展新MCPF-K成分KMCPF。如图 1(b)所示。
定义3 MCPF监控成分(MCPF-R) MR是主体进行认知活动的全过程中,将自己正在进行的认知活动作为意识对象,不断地对其进行积极、自觉地监察、控制和调节。MCPF-R(如图 1(c))包括跟踪目标任务和跟踪策略,其中跟踪策略包括更新行为(update behavior,UB),刺激行为(stimulate behavior,SB)和提取行为(extract behavior,EB)。
定义4 更新行为(UB) UB包括更新当前目标模板,或更新采样粒子权重和当前目标模板,或当前采样粒子集的观测图像特征替换为目标模板。
定义5 刺激行为(SB) SB或是以MCPF-K的KMCPF成分为基础,或MCPF-R促使MCPF-E产生意识e的行为,或是由MCPF-R促使MCPF-E产生意识并发展KMCPF的行为。如图 1细虚线箭头部分所示。
定义6 提取行为(EB) EB是MCPF-R获取MCPF-E意识e或MCPF-K的KMCPF成分的行为,以及将MCPF-K上升为MCPF-E的行为。如图 1细实线箭头部分所示。
2.2 MCPF模型的运行机制设粒子集合Φ0={Xi,i=1,2,...,N},MCPF-E表示为E0={T,F,P},其中E0=T表示匹配成功,E0=F表示匹配失败,E0=P表示困惑。MCPF模型的运行机制(如图 1所示)描述如下。
1)MCPF跟踪模型进行初始化。粒子集合Φ0的观测图像特征I0OM为初始目标模型,并将I0OM发展为初始认知模型I0CM,以及初始目标认知模型I0OCM和背景认知模型I0BCM作为认知知识成分,此认知成分可以来自目标检测的背景建模模型,本文的认知知识成分来自于文献[17]中的CGMM算法。
2)MCPF-R刺激采样粒子Xi(i=1,2,...,N)的观测模型Ij(j=1,2,...)与当前目标模型IsOM(s=1,2,...)匹配产生意识ej。
3)MCPF-R提取意识ej,权重计算得到MCPF的观测模型IkOM(k=1,2,...)及意识Ek0(k=1,2,...);如果Ek0=T,提取的是成功意识,MCPF-R选择不更新当前目标模板的跟踪策略,转步骤2)继续;如果Ek0=P,提取的是困惑意识,MCPF-R选择步骤4);如果Ek0=F,提取的是失败意识,MCPF-R选择步骤5)。
4)MCPF-R刺激观测模型IkOM(k=1,2,...)与目标认知模板I0OCM和背景认知模板I0BCM进行匹配。如果前者提取的ejOCM=T且后者提取的ejBCM=F,则MCPF-R选择当前观测模型更新目标模板的跟踪策略,转步骤2)继续;如果前者提取的ejOCM=F且后者提取的ejBCM=T,则MCPF-R选择不更新目标模板,采样粒子游走运动的跟踪策略,转步骤2)继续。
5)MCPF-R刺激采样粒子Xi(i=1,2,...,N)与目标认知模型I0OCM匹配产生MCPF-E意识ej。 6)MCPF-R提取MCPF-E的意识ej;如果ej=T,提取的是成功意识,MCPF-R选择将当前采样粒子集的观测图像特征更新为当前目标模板,转步骤2)继续;如果ej=F,提取的是失败意识,不进行目标模板的更新,扩大采样粒子搜索范围,转步骤2)继续。
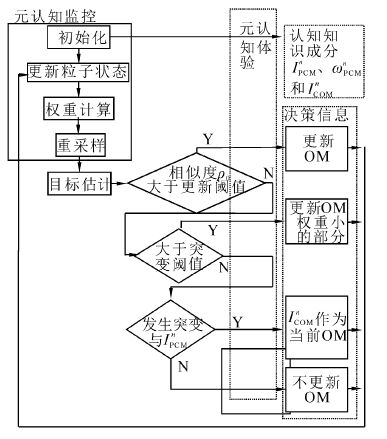
2.3 MCPF算法流程MCPF的MCPF-R提取MCPF-K中的运动模型,对N个粒子的位置状态进行更新,获得时刻k的粒子状态;取得时刻k的N个粒子观测图像特征与MCPF-K中提取的OM(即目标模型)进行相似度量,更新每个粒子的权值,然后根据粒子的权值对粒子集估计目标k时刻的最终状态。
1)初始化。建立MCPF的初始目标模板和状态转移模型。取时刻k0为初始帧,初始帧中目标的中心位置(x0,y0)为每个粒子的初始位置(xi0,yi0),初始帧中每个粒子的速度为(vix,0,viy,0)=(0,0),粒子集合Φk0的观测图像特征Ik0为初始目标模板,根据文献[17]CGMM算法生成MCPF目标认知模板I0OCM和背景认知模板I0BCM,每个粒子的初始化权重为1/N。
2)根据式(2)状态转移模型更新每个粒子的位置。
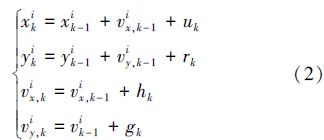
3)根据式(3)~(5)计算每个粒子的权重。
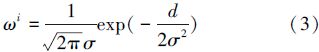


4)重采样。粒子集{Xik,ωik}得到新的粒子集{Xik,1/N},i=1,2,...,N,文中选用随机采样方法:

5)估计目标状态并输出目标当前位置,估计目标状态为

6)根据式(5)计算当前目标估计观测图像特征IK与当前目标模板I0K0的相似系数ρ0,输出决策信息:
a)如果ρ0≥λ0(λ0为更新阈值),目标跟踪正常,根据式8)更新目标模板:
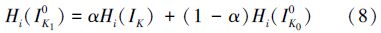
b)如果λ0>ρ0≥λ0(λ0为突变阈值),目标部分遮挡或者是发生形变,则根据式(5)计算当前目标估计观测图像特征IK与认知目标模板IiPCM的相似系数ρc。若ρc>λ0则认为是曾经被认知过目标,此时是发生了形变,将认知粒子模板的权重赋予该采样粒子,并将认知目标模板替换为目标模板;若ρc<λ0认为是未曾认知的遮挡或形变发生,根据式(9)进行目标模板的更新:
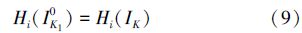
c)如果ρ0<λ1,目标消失、丢失或被完全遮挡,不进行目标模板的更新,扩大采样粒子搜索范围,发现目标立即恢复跟踪。
7)转步骤2)继续
。
|
| 图 2 MCPF算法流程 Fig. 2 MCPF algorithm flow |
为了测试MCPF算法的有效性,用VS 2013开发环境、VC++编程语言和OPENCV开发了一个实时目标跟踪系统。系统配置为I7处理器、8 GB内存,输入视频序列分辨率为320×240,选择视频序列IndoorTest进行实验,该视频序列中室内背景复杂,选择此视频序列进行了背景发生突变时的跟踪测试实验,部分实验结果如图 3所示。

|
| 图 3 测试实验结果 Fig. 3 Experimental results |
实验测试MCPF算法的MCPF-K中目标模型(如图 3(a)所示),选用目标颜色特征,可以有效克服目标形变的影响,且在非遮挡情况下实时更新目标颜色模板,以适应光照变化[6]。采用YCbCr颜色空间,将颜色分量分别量化为Nb、Nr级,目标模板基于CrCb空间的Nr×Nb级二维直方图和Y空间的Ny级一维直方图,相似度量使用Bhattacharyya距离。粒子数N=20。
为了降低背景对目标模型的干扰,文献[7]获取目标模板时通过调低模板四周背景信息的权重值来解决,并指定环形区域为背景区域,突变的背景信息没能更新到目标模板中,容易造成跟踪不稳定,尤其当突变背景与目标模板相似时,极易造成目标偏移甚至丢失(如图 3(d)所示);另外,如果突变背景信息更新不及时也会造成此类情况发生(如图 3(c)所示)。而MCPF算法是由文献[17]的CGMM算法生成的背景知识成分,对于背景区域的划分更精确,而且能够对目标模板中目标和背景信息进行认知,当背景突变时仍然能保持稳定的跟踪,如图 3(b)所示。
4 结束语本文受元认知理论启发,将目标跟踪作为认知活动,提出了具有元认知能力的粒子滤波目标跟踪算法(MCPF)。MCPF算法能够认知目标模型,监控PF迭代过程,提供有效的决策机制及实现稳定的跟踪。背景发生突变的跟踪测试实验表明了算法的有效性。该算法的提出对于进一步研究多运动目标检测与跟踪具有指导意义和应用价值。
| [1] | GORDON N J, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEE Proceedings F Radar and Signal Processing, 1993, 140(2): 107-113. |
| [2] | ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174-188. |
| [3] | ISARD M, BLAKE A. Condensation-conditional density propagation for visual tracking[J]. International Journal on Computer Vision, 1998, 29(1): 5-28. |
| [4] | MEI Xue, LING Haibin. Robust visual tracking and vehicle classification via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(11): 2259-2272. |
| [5] | YANG Hanxue, SHAO Ling, ZHENG Feng, et al. Recent advances and trends in visual tracking: a review[J]. Neurocomputing, 2011, 74(18): 3823-3831. |
| [6] | 常发亮, 马丽, 刘增晓, 等. 复杂环境下基于自适应粒子滤波器的目标跟踪[J]. 电子学报, 2006, 34(12): 2150-2153. CHANG Faliang, MA Li, LIU Zengxiao, et al. Target tracking based on adaptive particle filter under complex background[J]. Acta Electronical Sinica, 2006, 34(12): 2150-2153. |
| [7] | 齐美彬, 张莉, 蒋建国, 等. 分块跟踪中的目标模板更新方法[J]. 中国图象图形学报, 2011, 16(6): 976-982. QI Meibin, ZHANG Li, JIANG Jianguo, et al. Target template update method in fragment tracking[J]. Journal of Image and Graphics, 2011, 16(6): 976-982. |
| [8] | 牛长锋, 陈登峰, 刘玉树. 基于SIFT特征和粒子滤波的目标跟踪方法[J]. 机器人, 2010, 32(2): 241-247. NIU Changfeng, CHEN Dengfeng, LIU Yushu. Tacking object based on SIFT features and particle filter[J]. Robot, 2010, 32(2): 241-247. |
| [9] | 左军毅, 张怡哲, 梁彦. 自适应不完全重采样粒子滤波器[J]. 自动化学报, 2012, 38(4): 647-652. ZUO Junyi, ZHANG Yizhe, LIANG Yan. Particle filter based on adaptive part resampling[J]. Acta Automatica Sinica, 2012, 38(4): 647-652. |
| [10] | FLAVELL J H. Metacognitive aspects of problem solving[M]//RESNICK L B. The Nature of Intelligence. Hillsdale, USA: Erlbaum, 1976: 231-232. |
| [11] | 董奇. 论元认知[J]. 北京师范大学学报, 1989(1): 68-74. |
| [12] | 冯惠昌. 元认知与学习[J]. 内蒙古教育学院学报, 1992(3): 66-70. |
| [13] | 杜晓新. 元认知在认知活动中的作用—兼论如何培养学生的元认知能力[J]. 上海师范大学学报, 1992(3): 135-139. |
| [14] | 汪玲, 郭德俊. 元认知的本质与要素[J]. 心理学报, 2000, 32(4): 458-463. WANG Ling, GUO Dejun. The nature and components of metacognition[J]. Acta Psychological Sinica, 2000, 32(4): 458-463. |
| [15] | 杨宁. 元认知研究的理论意义[J]. 心理学报, 1995, 27(3): 322-328. YANG Ning. Theoretical meaning of the study on metacognition[J]. Acta Psychological Sinica, 1995, 27(3): 322-328. |
| [16] | 董文会, 常发亮, 李天平. 融合颜色直方图及SIFT特征的自适应分块目标跟踪方法[J]. 电子与信息学报, 2013, 35(4): 770-776. DONG Wenhui, CHANG Faliang, LI Tianping. Adaptive fragments-based target tracking method fusing color histogram and SIFT features[J]. Journal of Electronics & Information Technology, 2013, 35(4): 770-776. |
| [17] | 陈真, 王钊. 基于元认知模型的智能混合高斯背景建模[J]. 计算机系统应用. 2013, 22(9): 180-184, 159. CHEN Zhen, WANG Zhao. Metacognitive model-based intelligent Gaussian mixture background modeling[J]. Computer Systems & Applications, 2013, 22(9): 180-184, 159. |



