2. 北京交通大学 现代信息科学和网络技术北京市重点实验室, 北京 100044
2. Beijing Key Laboratory of Advanced Information Science and Network technology, Beijing Jiaotong University, Beijing 100044, China
近年来,随着社会复杂度的增大和人口密集度的增加,异常事件和突发事件也随之迅速增多,因此安防监控被提上了日程,成为人们关注的焦点。越来越多大规模的视频监控系统被建立,面对海量涌现的视频数据,加上工作人员精力有限,不可能时刻监控视频中发生的事件,因此如何去自动获取分析其中包含的内容成为一个亟待解决的问题。视频中大部分内容是人的行为活动,要让计算机理解视频中的人在什么场景做什么,并用自然语言表述出来,具有很重要的学术和应用价值。因此人体行为分析成为研究的热点。人体行为分析的一个关键点是从复杂的人体行为中提取重要的有区分力特征。目前已经有一些经典的特征分析方法,如主成分分析(PCA)、独立成分分析(ICA)等[1, 2, 3]。但是这些方法都是线性的特征分析技术,对于非线性处理也许会导致错误的结果。为了处理非线性系统,提出了一些改进的方法,如基于核的主成分分析(KPCA)。基于核的主成分分析首先由B. Scholkopf等[4]提出,在高维特征空间中使用核函数计算主成分,这个高维特征空间和输入空间是非线性相关的。
最近,一种新的数据特征分析方法,即慢特征分析(slow feature analysis,SFA)[5]被提出。慢特征分析的主要目的是从输入信号中提取最佳的缓慢变化的特征作为信号的不变表示。随时间变化的信号的不变特征对于很多模式分类任务非常有用,并且慢特征分析已经被成功应用于姿势识别和图像特征提取等一些领域[6, 7, 8, 9, 10, 11, 12]。Zhang等[13]把慢特征分析应用于人体行为识别,并取得了很好的效果。基于慢特征分析能够提取输入信号的不变量信息,并且具有平移、旋转、缩放、光照等不变性,具有方向选择性和边缘方向选择性的特点,因此本文提出了视频中人体行为的慢特征提取方法。
1 慢特征分析(SFA)原理慢特征是利用慢特征分析(SFA)方法从输入信号中获取的能够表征信号发生源某些固有属性的特征。慢特征能够表征输入信号的不变量信息,对于数据分析和模式识别都有非常重要的作用。慢特征的有效提取是后续行为分析的基础,起着关键性的作用。
1.1 SFA的数学描述慢特征分析算法的目标是从输入的时序信号x(t)=(x1(t),x2(t),…,xI(t))T中提取出变化比较缓慢的隐含成分,即最具有不变量性质的信息。其数学描述如下[5]。
给定一个I维输入信号x(t)=(x1(t),x2(t),…,xI(t))T,其中t表示时间,变化范围[t0,t1]。找到一个J维的变换函数g(x)=(g1(x),g2(x),...,gJ(x))T,从而产生J维的输出信号y(t)=(y1(t),y2(t),...,yJ(t))T,其中yj(t):=gj(x(t))。优化问题框架如下:
对于每一个j∈{1,2,...,J},

 表示yj(t)关于时间t的一阶导数,尖括号〈·〉表示在时间上求均值。约束条件(2)和(3)避免了yj(t)等于常量。条件(4)说明只要i≠j,则分量yi(t)和分量yj(t)的协方差为零,即yi(t)和yj(t)互不相关,由于i和j是任意的,所以能够保证输出信号各分量间是不相关的,因此每个分量携带不同的信息。同时也产生了一个顺序,y1(t)是最佳的输出信号,即变化最慢的信号,y2(t)其次,依次类推。
1.2 SFA算法具体实现步骤
表示yj(t)关于时间t的一阶导数,尖括号〈·〉表示在时间上求均值。约束条件(2)和(3)避免了yj(t)等于常量。条件(4)说明只要i≠j,则分量yi(t)和分量yj(t)的协方差为零,即yi(t)和yj(t)互不相关,由于i和j是任意的,所以能够保证输出信号各分量间是不相关的,因此每个分量携带不同的信息。同时也产生了一个顺序,y1(t)是最佳的输出信号,即变化最慢的信号,y2(t)其次,依次类推。
1.2 SFA算法具体实现步骤慢特征分析算法实质上是一个学习问题,也即变分法的最优化问题,一般来讲很难解决。然而对于输入输出函数元素gj被限定为有限个非线性函数的线性组合,问题就大大简化了。在这个限定下,解决最优化问题的算法如下。
给定一个I维输入信号x(t)=(x1(t),x2(t),…,xI(t))T,一个J维变换函数g(x)=(g1(x),g2(x),...,gJ(x))T。
1)如果变换是线性的,即gj(x)=wjTx,其中x是输入,wj是权值。不失一般性,假设x均值为0,方差为1,即〈x〉t=0,〈x2〉t=1。因为yj(t)=gj(x(t))=wjTx(t),所以方程(2)中,
令B=〈xxT〉t,则〈yi(t)yj(t)〉=wiTBwj,只要选择合适的权值,使得wiTBwj=δij,则式(4)中的限制条件被满足。
式(1)中的目标函数:
 ,则
,则 ,把式(3)中的限制条件整合到目标函数(1)中,则有
,把式(3)中的限制条件整合到目标函数(1)中,则有
由线性代数可知,能够使上式取得最小值的权值向量wj对应于式(5)一般特征值问题的特征向量,此时式(3)中的限制条件也被满足。

2)非线性变换可以视为非线性空间的线性变换[5]。函数h(x)的非线性扩展定义为
慢特征函数通过以下步骤获得。
a)使用非线性函数h(x)对原始信号进行扩展,并把h(x)归一化,使其均值为0,即z:=h(x)-h0,其中h0=〈h(x)〉t,归一化使条件(2)有效。本文使用二次扩展,即h(x)=(x1,x2,...,xI,x1x1,x1x2,...,xIxI)。
b)解决一般化的特征值问题AW=BWΛ,其中, ,B:=〈zzT〉t。假设矩阵A和矩阵B的维数都是M,前K个特征向量w1,w2,...,wK(K≪M)和最小的特征值相联系,即λ1≤λ2≤…≤λK,对应的非线性慢特征函数g1(x),g2(x),...,gK(x):
,B:=〈zzT〉t。假设矩阵A和矩阵B的维数都是M,前K个特征向量w1,w2,...,wK(K≪M)和最小的特征值相联系,即λ1≤λ2≤…≤λK,对应的非线性慢特征函数g1(x),g2(x),...,gK(x):

这些慢特征函数能够满足约束条件(2)~(4),而且能使式(1)中的目标函数最小。
1.3 改进的慢特征分析算法(D-SFA)慢特征分析方法是一种非监督式学习策略,不能编码有监督的信息,为了把监督信息引入到学习中,提出了D-SFA(discriminative SFA)学习策略[13],其数学描述为:已知输入信号xc(t)=xc1(t),xc2(t),...,xcI(t),c∈1,2,...,C,目标是找到一系列的J维输入输出函数gc(x)=gc1(x),gc2(x),...,gcJ(x)T,使得Δ(gcj(xc))-γ×Δ(gcj(xc′))最小,即对于每一个j∈{1,2,...,J},使式(8)最小:

求解最小值问题可以转化为求解一般的特征值问题:AW=BWΛ,其中A=(〈xcxcT〉t-γ×〈xc′xc′T〉t),B=〈xc∪c′xc∪c′T〉t,Λ是特征值组成的对角矩阵,W是相应的特征向量。 2 视频中人体行为的慢特征提取
本文提出的视频中人体行为慢特征的提取主要包括3个部分:收集训练立方体、D-SFA算法提取慢特征和构建ASD特征表示。
2.1 收集训练立方体收集训练立方体是由视频图像序列构建出原始输入信号x(t)的一种方法。首先对原始视频进行处理,得到帧差图像序列。以选定的某一帧图像作为初始帧,检测其特征点[14],然后使用光流法对特征点进行跟踪[15, 16],从而得到视频中所有特征点对应的轨迹集合。对于轨迹集合中的每条轨迹,提取其中各个轨迹点w×w邻域内的像素值,形成一系列的像素块,考虑到时间信息,通过Δt个相继帧对每个点的像素块序列进行整合,本文取Δt=3。进一步对所有的特征点进行整合后得到训练立方体,即构建出了输入向量x(t)。图 1给出了训练立方体的获取过程。

|
| 图 1 训练立方体的获取过程 Fig. 1 the process of obtaining training cuboids |
慢特征分析方法是实现提取慢特征任务而提出的一种学习算法。SFA算法是一种非监督学习算法,它在人体行为视频中提取慢特征的思想是:不同种类的行为视频收集到的训练立方体混合在一起用于慢特征函数的机器学习,然后用学习出来的慢特征函数提取出慢特征。由于不能编码有监督信息,所以提取出来的慢特征在行为间没有很好的区分力。D-SFA算法在学习过程中引入了监督信息,其在人体行为视频中提取慢特征的思想是:对于每一类行为收集到的训练立方体分别用于慢特征函数的学习,这样学习出的慢特征函数具有行为类间的区分力,即对类内行为具有选择性。
2.3 ASD特征表示由于慢特征分析能够使均方导数最小,所以1个立方体对相应慢特征函数的拟合度可以通过变换立方体的平方导数来衡量[13]。如果值很小,则说明这个立方体和慢特征函数拟合得很好。对于第i个立方体Ci和第j个慢特征函数,定义平方导数:
然后把平方导数在所有的立方体上进行累加,从而形成ASD特征为

本文选用魏茨曼科学院行为识别数据库(Weizmann human action database)进行慢特征的提取实验,用于验证慢特征分析方法在人体行为视频中提取慢特征的有效性。该数据库包含10种单人行为,包括弯腰、奔跑、单脚跳、双脚跳、原地跳、挥手跳、侧行、行走、单臂挥舞和双臂挥舞。每种行为分别由9位不同的人完成。图 2给出了每类行为的图像样本。

|
| 图 2 Weizmann人体行为数据库样图 Fig. 2 Sample images of each type of action in the Weizmann database |
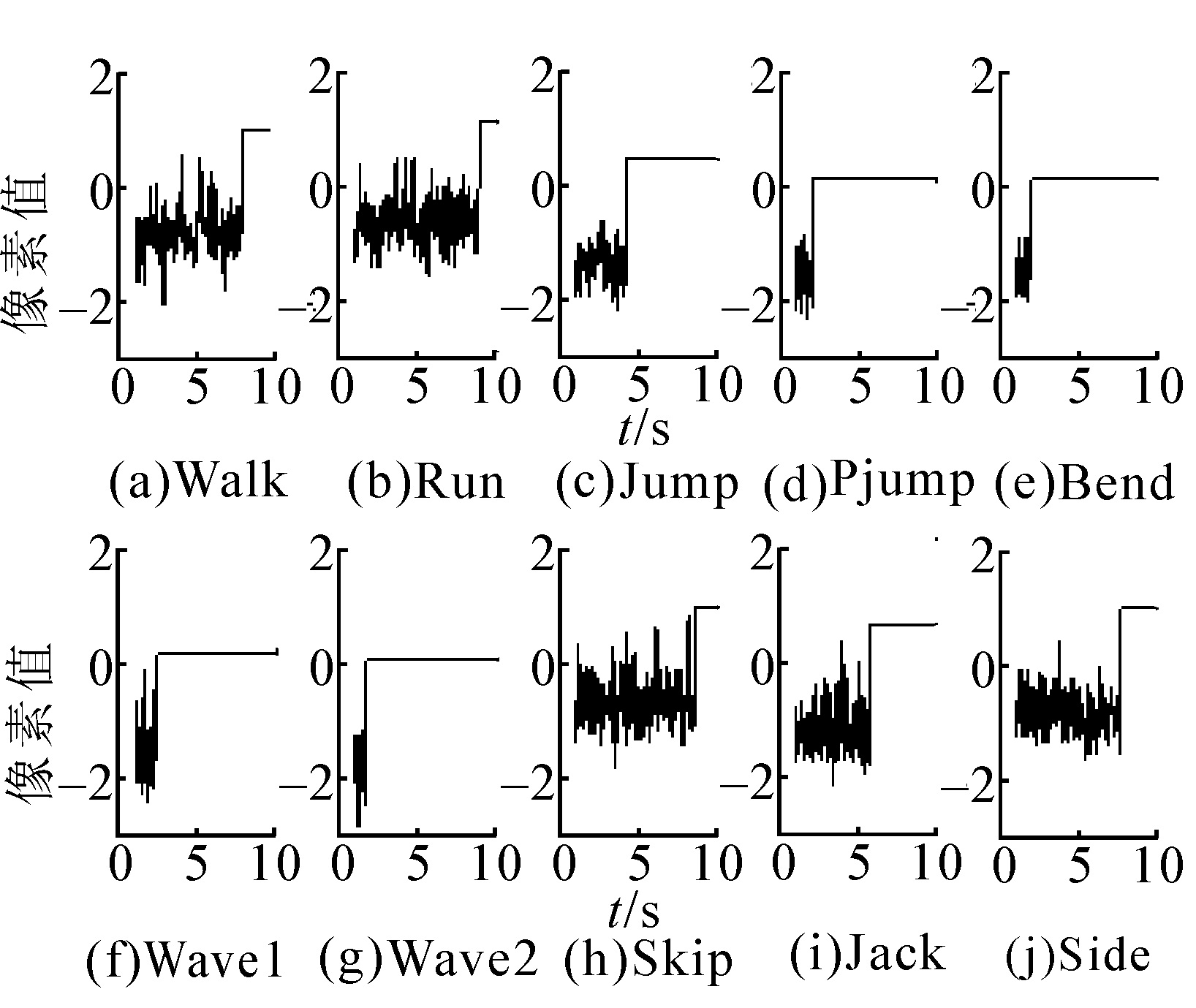
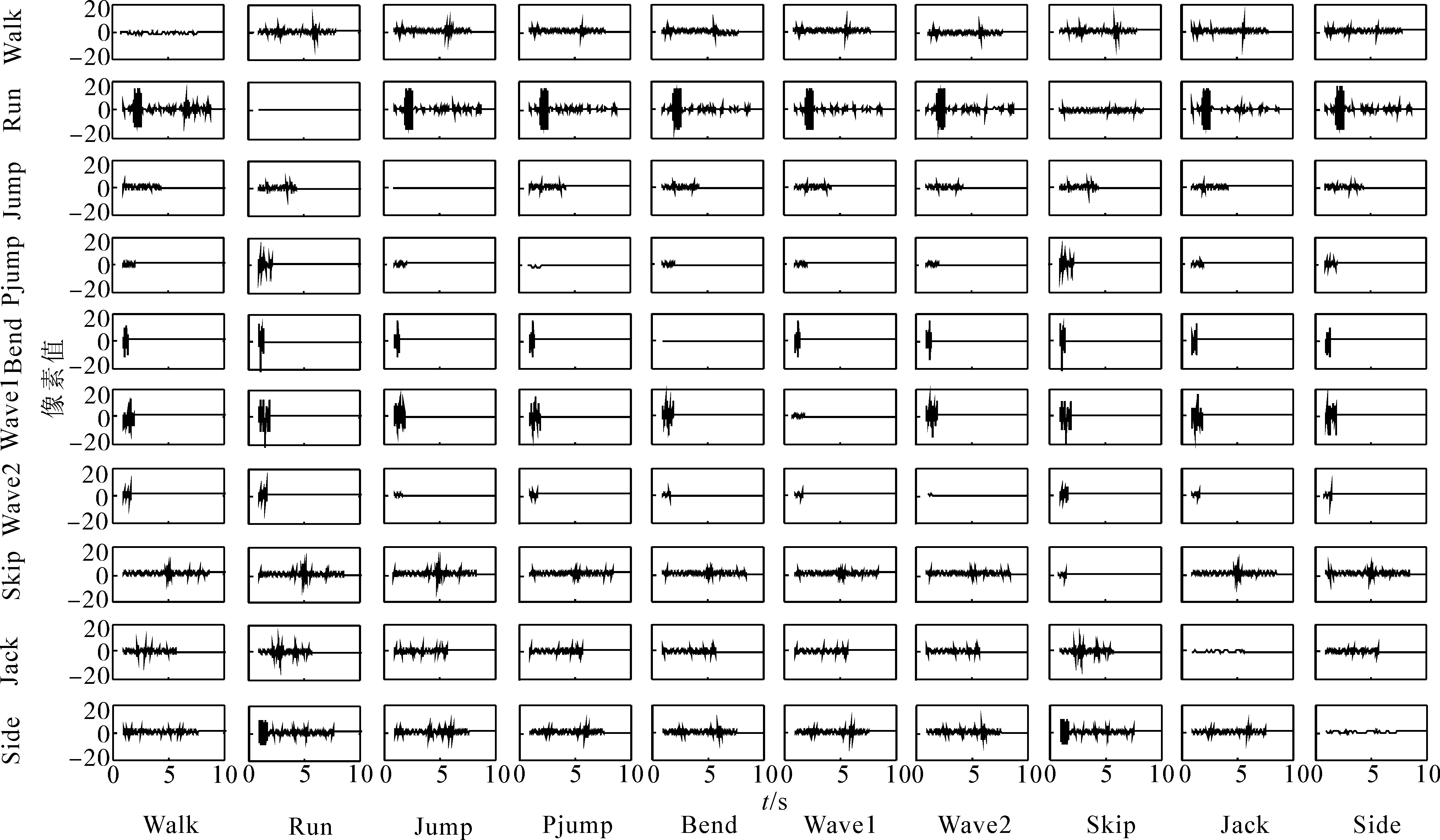
为了验证慢特征分析方法在人体行为视频中提取慢特征的有效性,使用3.1介绍的数据库进行实验。实验分别从SFA和D-SFA对不同行为提取慢特征的效果对比和使用D-SFA计算出的ASD特征的模值对比2个方面,说明慢特征分析方法能够有效提取慢特征,且D-SFA较之SFA效果更好。图 3和4为2种算法提取的慢特征随时间的变化图对比,
图 3中使用SFA算法对不同的行为进行慢特征的提取。可以看出不同行为的慢特征随时间的变化具有相似性,区分力比较小。这是因为SFA算法是一种非监督式学习算法,不能编码任何监督信息,其慢特征函数是由所有行为混合在一起进行机器学习得到的,因此慢特征函数被不同行为所共有,降低了行为间的区分力。
|
| 图 3 SFA算法提取的慢特征随时间变化 Fig. 3 the diagram of slow features extracted by SFA vary with time |
图 4中使用D-SFA算法进行慢特征的提取。图中包含10×10个子图,其中坐标为(i,j)的子图表示第j类行为经第i类行为的慢特征函数变换得到的慢特征随时间的变化图。可以看出对角线上的图随时间基本不变,这说明D-SFA算法具有行为类间的选择性,每种行为训练出的慢特征函数能使该行为变慢,而使其他行为变化相对较快。这是因为D-SFA算法是对每一类行为都进行机器学习,分别得到对应的慢特征函数,因此提取出的慢特征具有很好的区分力。
表 1是D-SFA算法计算出来的不同类行为的ASD特征的模值.该表是由10×10个单元构成,第(i,j)个单元表示第j类行为的立方体经第i类行为的慢特征函数变换后计算出来的ASD特征的模值。由表中数据可知,第j列中,第(j,j)个单元中的数据比该列其他数据都要小得多。这说明D-SFA算法学习出的慢特征函数只能使该类行为的ASD特征值变慢,因此行为类间具有很好的区分力。
|
| 图 4 D-SFA算法提取的慢特征随时间变化 Fig. 4 the diagram of slow features extracted by D-SFA vary with time |
| Action | Walk | Run | Jump | Pjump | Bend | Wave1 | Wave2 | Skip | Jack | Side |
| Walk | 0.070 900 | 151.790 0 | 133.570 0 | 132.840 0 | 127.840 0 | 128.470 0 | 124.620 0 | 135.160 0 | 160.230 0 | 145.480 0 |
| Run | 229.140 0 | 0.062 400 | 218.820 0 | 229.860 0 | 224.930 0 | 237.400 0 | 230.600 0 | 232.590 0 | 252.640 0 | 232.000 0 |
| Jump | 699.784 5 | 673.711 9 | 0.012 000 | 596.557 3 | 574.379 3 | 594.044 5 | 583.238 9 | 637.634 4 | 657.620 8 | 605.668 7 |
| Pjump | 599.942 5 | 657.441 9 | 491.771 5 | 0.001 600 | 541.067 3 | 553.955 2 | 532.864 2 | 633.454 2 | 747.772 2 | 637.911 7 |
| Bend | 671.993 2 | 810.703 0 | 716.960 0 | 680.960 2 | 0.000 700 | 936.513 2 | 640.215 0 | 646.039 7 | 836.871 7 | 669.577 6 |
| Wave1 | 111.170 0 | 103.880 0 | 109.310 0 | 109.600 0 | 993.861 6 | 0.002 800 | 106.190 0 | 929.660 7 | 100.890 0 | 908.275 0 |
| Wave2 | 671.422 7 | 658.995 6 | 637.138 4 | 596.024 6 | 512.697 4 | 710.915 5 | 0.000 784 | 677.386 6 | 605.973 7 | 707.146 2 |
| Skip | 154.830 0 | 152.960 0 | 135.650 0 | 154.300 0 | 144.120 0 | 144.650 0 | 136.380 0 | 0.062 100 | 159.480 0 | 169.340 0 |
| Jack | 199.040 0 | 221.760 0 | 186.610 0 | 179.800 0 | 180.100 0 | 195.600 0 | 194.540 0 | 218.020 0 | 0.011 900 | 213.670 0 |
| Side | 186.260 0 | 200.920 0 | 173.890 0 | 171.580 0 | 169.160 0 | 165.030 0 | 172.510 0 | 181.580 0 | 198.180 0 | 0.035 200 |
本文提出了视频中人体行为的慢特征提取方法,首先收集训练立方体,然后分别用SFA算法和D-SFA算法进行慢特征函数的机器学习,经慢特征函数变换后得到慢特征,并进一步构建ASD特征。实验结果表明D-SFA算法能更有效地提取出人体行为的慢特征。由于特征点跟踪的过程中,少量特征点在后续帧中会出现漂移现象,对后面的处理会产生一定的影响,今后将进一步研究以取得更好的效果。
| [1] | VENKAtASUBRAMANIAN V, RENGASWAMY R, KAVURI S N, et al. A review of process fault detection and diagnosis: Part III: process history based methods[J]. Computers & Chemical Engineering, 2003, 27(3): 327-346. |
| [2] | CHERRY G A, QIN S J. Multiblock principal component analysis based on a combined index for semiconductor fault detection and diagnosis[J]. IEEE transactions on Semiconductor Manufacturing, 2006, 19(2): 159-172. |
| [3] | DUNIA R, QIN S J. Joint diagnosis of process and sensor faults using principal component analysis[J]. Control Engineering Practice, 1998, 6(4): 457-469. |
| [4] | SCHLKPOF B, SMOLA A, MVLLER K R. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319. |
| [5] | WISKOtt L, SEINOWSKI t L. Slow feature analysis: unsupervised learning of invariances [J]. Neural Computation, 2002, 14(4): 715-770. |
| [6] | BERKES P, WISKOtt L. Slow feature analysis yields a rich repertoire of complex cell properties[J]. Journal of Vision, 2005, 5(6): 579-602. |
| [7] | XIA Qi, GAO Jianbin, XU Chunxiang. A new watermarking algorithm based on slowly feature analysis[C]//International Conference on Apperceiving Computing and Intelligence Analysis. Chengdu, China, 2008: 70-72. |
| [8] | GAO Jianbin, LI Jianping, XIA Qi. Slowly feature analysis of Gabor feature for face recognition[C]//2008 International Conference on Apperceiving Computing and Intelligence Analysis. Chengdu, China, 2008: 177-180. |
| [9] | HUANG Yaping, ZHAO Jiali, tIAN Mei, et al. Slow feature discriminant analysis and its application on handwritten digit recognition [C]//International Joint Conference on Neural Networks. Atlanta, USA, 2009: 1294-1297. |
| [10] | MA Kuijun, tAO Qing, WANG Jue. Nonlinear blind source separation using slow feature analysis with random features[C]//2010 20th International Conference on Pattern Recognition. Istanbul, turkey, 2010: 830-833. |
| [11] | KVHNL t, KUMMERt F, FRItSCH J. Monocular road segmentation using slow feature analysis[C]//2011 IEEE Intelligent Vehicles Symposium (IV). Baden-Baden, Germany, 2011: 800-806. |
| [12] | DENG Xiaogang, tIAN Xuemin, HU Xiangyang. Nonlinear process fault diagnosis based on slow feature analysis[C]//2012 10th World Congress on Intelligent Control and Automation. Beijing, China, 2012: 3152-3156. |
| [13] | ZHANG Zhang, tAO Dacheng. Slow feature analysis for human action recognition[J]. IEEE transactions on Pattern Analysis and Machine Intelligence, 2012, 34(3): 436-450. |
| [14] | 王丽辉, 袁保宗. 三维散乱点云模型的特征点检测[J]. 信号处理, 2011, 27(6): 932-938.WANG Lihui, YUAN Baozong. Feature point detection for 3D scattered point cloud model[J]. Signal Processing, 2011, 27(6): 932-938. |
| [15] | 马龙, 王鲁平, 陈小天, 等. 噪声环境下光流场估计方法[J]. 信号处理, 2012, 28(1): 87-91.MA Long, WANG Luping, CHEN Xiaotian, et al. Determining optical flow field in the presence of noise[J]. Signal Processing, 2012, 28(1): 87-91 |
| [16] | 江志军, 易华蓉. 一种基于图像金字塔光流的特征跟踪方法[J]. 武汉大学学报:信息科学版, 2007, 32(8): 680-683.JIANG Zhijun, YI Huarong. An image pyramid-based feature detection and tracking algorithm[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8): 680-683. |



