2. 江苏科技大学 计算机科学与工程学院, 江苏 镇江 212000
2. School of Computer Science and Engineering, Jiangsu University of Science and Technology, Zhenjiang 212000, China
Lowe提出的尺度不变特征变换(scale invariant feature transform,SIFT)[1]是一种鲁棒性强的图像局部特征提取算法,具有对旋转、光照、尺度变化等保持不变性[2],广泛应用于三维重建、目标识别、图像融合等领域[3]。SIFT算法由特征点检测及描述与特征点匹配两部分构成,其中,SIFT特征点匹配实质上可以转化为在高维空间中搜索特征点最近邻的问题,并且在很多情况下,只需要得到查询特征点的近似最近邻就足够了[4]。据此近年来提出了一些相关算法,其中,Lowe提出的最优节点优先算法(best bin first,BBF)[5]在K-D树索引的基础上,使用优先队列和限制回溯查询次数来提高搜索最近邻的效率。va+-file算法[6]将数据集转换到KLT域,然后采用均匀量化划分来提高va-file算法[7]的过滤效率。iDistance算法[8]对高维数据空间进行划分,使用B+-tree结果来组织参考点并搜索最近邻。LSH(locality sensitive hashing,LSH)算法[9, 10]通过Hash函数将邻近高维点集映射到Hash表的同一个桶中,从而提高搜索最近邻效率。基于聚类分析的B+-tree算法[11]采用类B+-tree索引结构,通过更加细致的划分数据来加快搜索速度。MRSVQH[12]根据选择子向量的L2范数来量化和散列特征向量,仅考虑具有与查询向量相同Hash值的集合,从而提高了搜索速度。
本文在以上研究的基础上,提出了一种基于参考点距离的SIFT特征点匹配算法—DRP算法,并通过实验与经典的BBF算法相比,来验证基于DRP算法的SIFT特征点匹配效果。
1 DRP算法 1.1 DRP算法原理
设d维欧式空间Rd中2个点P1=(x1,x2,…,xd),P2=(y1,y2,…,yd),两点对应的向量分别为V1=[x1 x2 … xd],V2=[y1 y2 … yd]。则P1、P2两点之间的欧式距离D(P1,P2)为
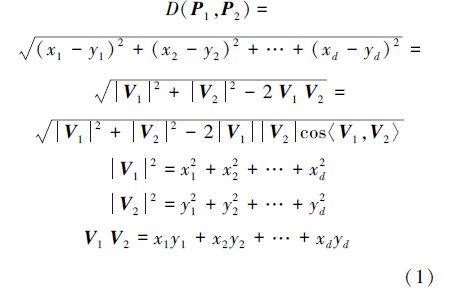
由式(1)可知,若|V1|确定且V1与V2的夹角一定时,当|V2|→|V1|cos〈V1,V2〉时,向量V1与V2对应的P1与P2两点之间的距离D(P1,P2)取最小值。
设d维欧式空间Rd中的一个点集合Fd={Pi|Pi∈Rd,i=1,2,…,n},对于∀Pquery∈Rd,需要在Fd中搜索Pquery的最近邻。设定一个参考点Pr,则对于每一个需要搜索的Pquery,Pquery与参考点Pr构成向量PrPquery是确定的(长度和方向),若Fd中所有点与设定参考点Pr构成的向量PrPi与PrPquery之间的夹角都为θ时,则使向量|PrPi|→|PrPquery|cosθ的点Pi就是Pquery的最近邻。
若集合Fd中所有特征点与设定参考点Pr构成的向量PrPi与PrPquery之间的夹角不都为θ时,即不相等时,上述结论并不一定成立。如图 1的三维空间所示。
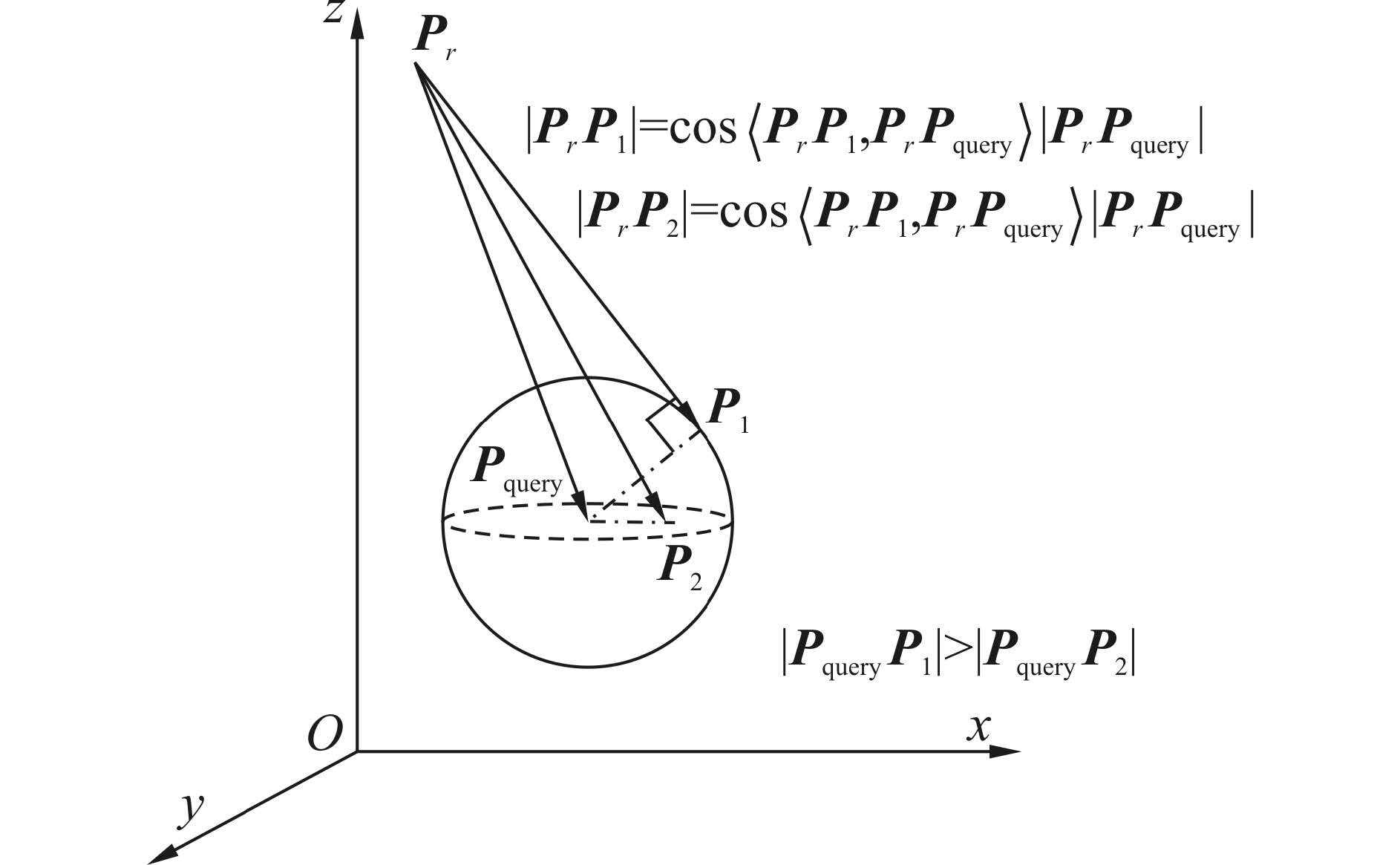
|
| 图 1 不同夹角时的最小距离 Fig. 1 The minimum distance of different angle |
尽管|PrP1|=cos〈PrP1,PrPquery〉|PrPquery|,而|PrP2|>cos〈PrP1,PrPquery〉|PrPquery|。但是,P2相对于P1更靠近Pquery。
为了尽可能的得到Pquery的最近邻,本文将搜索范围扩大到集合Fd′中的所有点。如图 2所示。
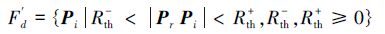
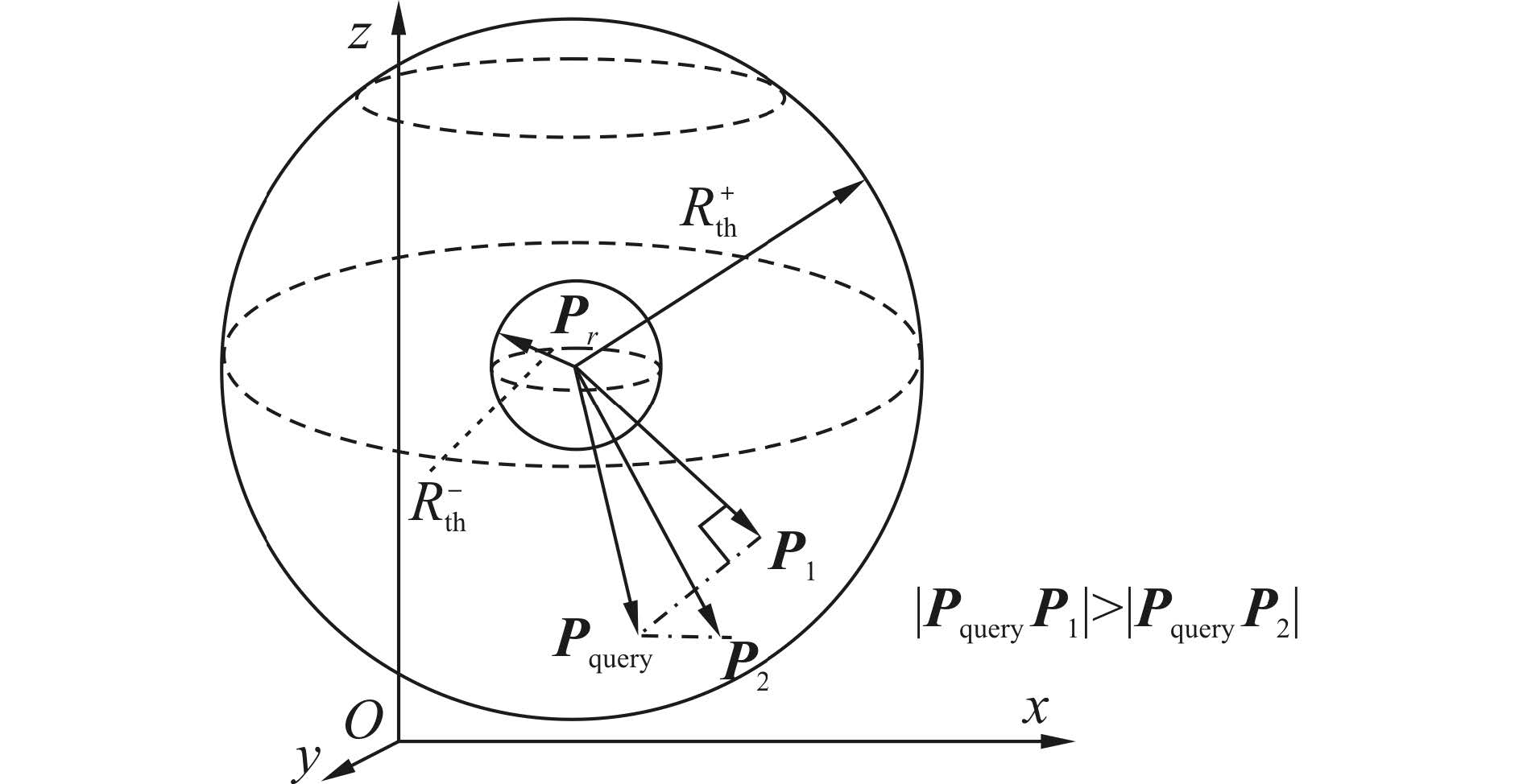
|
| 图 2 在一定区域内搜索最近邻 Fig. 2 Search the nearest neighbor in a specified area |
若将搜索范围扩大到以Pr为球心,Rth-为半径的球外,Rth+为半径的球内区域,则可得到Pquery的真正最近邻P2。随着Rth-的减小和Rth+的增大,搜索到Pquery的真正最近邻的概率也随之增大。由此可知,当Fd中所有点与设定参考点Pr构成的向量PrPi与PrPquery之间的夹角不相等时,只需要选择一个合适的搜索范围Rth-与Rth+,仍然可以搜索到Pquery的真正最近邻。
1.2 DRP算法描述设d维欧式空间Rd中的2个点集合:
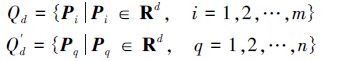
对于∀Pq∈Qd′,需要在集合Qd中搜索其最近邻。引入一个参考点(可随机选取)Pr∈Rd,若Pnearest(Pnearest∈Qd)是Pq的最近邻,则Pnearest应该出现在Pq的附近,即向量PrPq与向量PrPnearest之间的夹角〈PrPq,PrPnearest〉应该趋向于零,此时|PrPnearest|=|PrPq|×cos〈PrPq,PrPnearest〉→|PrPq|。因此,当|PrPnearest|=|PrPq|时,点Pnearest为查询点Pq的最近邻。由此,对于∀Pq∈Qd′,不需要逐一计算Pq与Qd集合中所有点的距离,而只要计算Pq与参考点Pr之间的距离Drq,然后在点集合Qd″中搜索,就可能得到Pq的真正最近邻,即Pq的真正最近邻落在集合Qd″所表示的范围中。
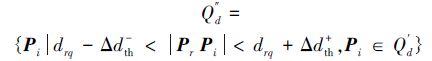
以图 3所示的三维空间为例,如果搜索向量Pq的最近邻,只需要在Pr为球心,半径为drq-Δdth-的球以外和半径为drq+Δdth-以内的空间搜索,就可以得到Pq的真正最近邻。
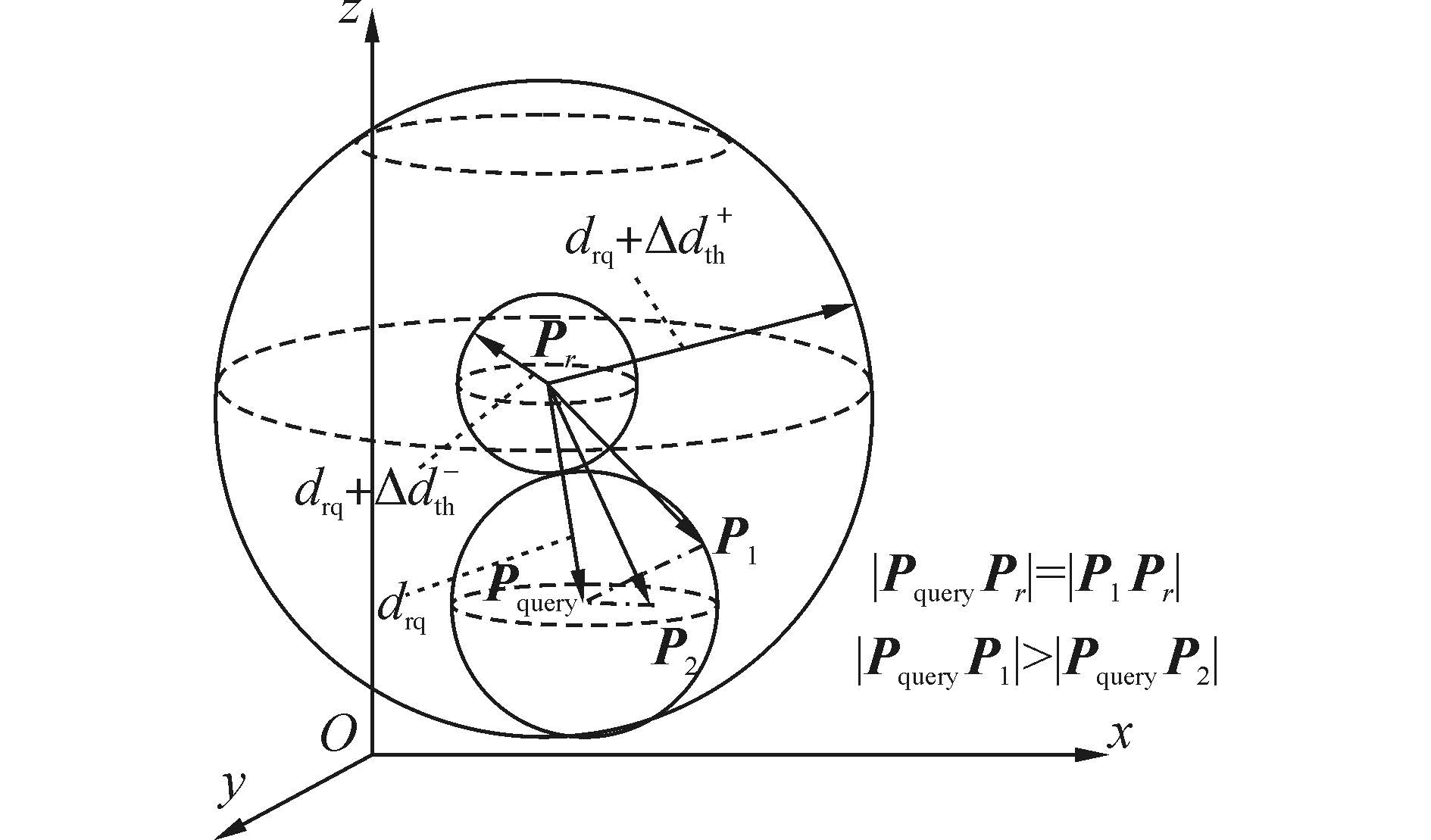
|
| 图 3 DRP算法搜索最近邻 Fig. 3 Search the nearest neighbor with DRP algorithm |
基于以上分析,在向量集合Fd中搜索向量Vq的最近邻的步骤如下:
1)在d维欧式空间Rd中任意选取一点Pr作为参考点,设定一个阈值th(正整数)。
2)对于任一属于集合Fd中的点Pi(i=1,2,…,m),计算其与参考点Pr之间的距离,保存于数组Dri中,并建立Dri与Pi的映射。
3)使用快速排序算法对Dri中的距离按升序(或降序)进行排序,得到Driorder。
4)从待匹配点集合Fd′中任取一待匹配点Pquery,计算Pquery与参考点Pr之间的距离Dqr=|PrPquery|。
5)使用二分查找法从Driorder中快速查找Drq的最近邻Drj,并得到Drj对应的点Pjnearest及其索引index(j)。
6)对Driorder中索引范围在[index(j)-th,index(j)+th]对应的所有点中,利用穷举搜索法查找Pquery的最近邻。
在步骤6)中涉及到距离的计算,为进一步提高算法的效率,均采用如下所述的距离累计算法。当d维点Px与Pquery的前i(i∈[1,d])维的欧式距离已经超过上一次比较的最小距离时,无论后面d-i维的距离情况如何,将必定大于已经产生的最小距离。因此,也无需计算它们后面d-i维的距离,直接剔除跳出,进行下一特征点的比较。
2 SIFT特征点快速匹配算法SIFT算法提取的图像特征点包括极大值与极小值2种类型,显而易见,只有极值类型相同的特征点才可能正确匹配。因此,本文在特征点匹配之前进行特征点类型的判断,仅当2个特征点具有相同类型时,才进行接下来的匹配运算,否则直接跳出,转而比较下一个特征点。这在一定程度上可以提高匹配的效率。
对于2幅含有同一场景的图像Iq(x,y)和Is(x,y),本文介绍的DRP算法按如下步骤进行。
1)使用SIFT算法分别提取图像Iq(x,y)与图像Is(x,y)的特征点,生成的特征点构成的集合分别为Pq128和Ps128。
2)对于∀Pi∈Pq128,使用本文介绍的DRP算法在集合Ps128中搜索得到查询点Pi的最近邻特征点Pnearest,对应的最近邻距离为dnearest,次近邻特征点Pnearest2,对应的次近邻距离dnearest2,若比值dnearest/dnearest2小于已知的阈值rth,则认为Pi与Pnearest两点之间正确匹配。
3)采用随机抽样一致性原则(random sample consensus,RANSAC)算法剔除误匹配的特征点。
3 实验结果与分析本文实验采用的代码由GitHub上Rob Hess维护的Opensift库[13]改进而来。实验采用的测试图片来自牛津大学VGG实验室的Affine Covariant Features(ACF)图片库[14]。实验硬件环境为CPU Inter(R) Core(TM)2 T6600,主频2.20 GHz,内存2 GB DDR3 RAM;软件环境为OS Windows7 32 bit、IDE Microsoft Visual Studio 2010、 GTK+2.24图形工具包和Opencv2.4机器视觉库。
为了验证DRP算法的有效性,本文进行了在不同搜索阈值th下,DRP算法与经典BBF算法的对比实验。简便起见,所有实验中的参考点均采用坐标原点,即Pr=xrj,xrj=0,j=1,2,…,128。其中,交叉验证两算法的最近邻与次近邻距离阈值比rth保持为0.56。BBF算法中除搜索阈值KDTREE_BBF_MAX_NN_CHKS变化外,其他所有参数保持默认。实验中搜索阈值th以50为步长在[50, 500]范围内变化,在不同搜索阈值th条件下,对Bikes、Trees、Graf、Bark、Boat、Leuven 6组图片每组中的Img1/Img2、Img1/Img3、Img1/Img4 3对图片各进行10次SIFT特征点匹配实验。统计得到特征点的正确匹配率、正确匹配特征点总数以及平均每幅图像匹配时间与搜索阈值th的关系如图 4所示。
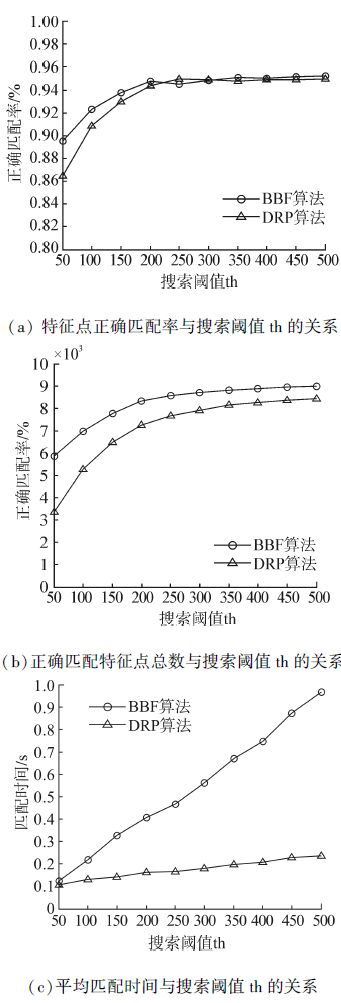
|
| 图 4 DRP算法与BBF算法实验对比结果 Fig. 4 The comparison results of DRP algorithm and BBF algorithm |
由图 4(a)可知,在特征点正确匹配率方面,DRP算法与BBF算法具有相同的趋势。当搜索阈值th小于200时,随着th的增大而增大;当搜索阈值th大于200时,特征点正确匹配率很难得到进一步的改善,趋于稳定。总体来看,这2个算法在特征点匹配率的表现上相差无几。由图 4(b)可知,在正确匹配特征点总数方面,DRP的算法略逊于BBF算法,但是,随着搜索阈值th的增大,两者的差距逐渐缩小。由图 4(c)可知,在匹配时间上,DRP算法与BBF算法都随着搜索阈值th的增大而呈线性增长趋势,但是,BBF的增长速率显著大于DRP算法,由此可知,在匹配时间上,DRP算法较BBF算法具有明显的优势。综上所述,相对于经典的BBF算法,本文介绍的DRP算法能获得满意匹配效果的同时,有效降低匹配时间。
4 结束语本文介绍了一种基于参考点距离的SIFT特征点匹配算法,并使用牛津大学VGG实验室的ACF图片库进行SIFT特征点匹配实验。实验结果表明,与经典BBF最近邻搜索算法相比,使用本文介绍的DRP算法进行SIFT特征点匹配,不仅可以获得满意的匹配效果,并且可以有效地降低匹配时间消耗,提高匹配速度。尤其在搜索阈值th较大的情况下,DRP算法在时间成本上较经典的BBF算法具有明显的优势。另外,DRP算法还有一些可以改进的地方,如对提取的SIFT特征点分布情况进行分析、参考点选择方法的分析等都可能进一步提高特征点的匹配效率。对于不同的特征点分布情况,如何选取一个合适的参考点,从而尽可能改善匹配效果是下一步的工作重心。
| [1] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. |
| [2] | 吴伟交, 王敏, 黄心汉, 等. 基于向量夹角的SIFT特征点匹配算法[J]. 模式识别与人工智能, 2013, 26(1): 123-127.WU Weijiao, WANG Min, HUANG Xinhan, et al. SIFT feature matching algorithm based on vector angle. Pattern Recognition and Artificial Intelligence, 2013, 26(1): 123-127. |
| [3] | KRYSTIAN M, CORDELIA S. A performance evaluation of local descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615-1630. |
| [4] | GIONIS A, INDYK P, MOTWANI R. Similarity search in high dimensions via hashing[C]//Proceedings of the 25th International Conference on Very Large Data Bases. San Francisco, USA, 1999: 518-529. |
| [5] | BEIS J S, LOWE D G. Shape indexing using approximate nearest-neighbor search in high-dimensional spaces[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. San Juan, Puerto Rico, 1997: 1000-1006. |
| [6] | FERHATOSMANOGLU H, TUNCEL E, AGRAWAL D, et al. Vector approximation based indexing for non-uniform high dimensional data sets[C]//Proceedings of the International Conference on Information and Knowledge Management. McLean, USA, 2000: 202-209. |
| [7] | WEBER R, SCHEK H J, BLOTT S. A quantitative analysis and performance study for similarity-search methods in high dimensional spaces[C]//Proceedings of the International Conference on Very Large Databases. New York, 1998: 194-205. |
| [8] | JAGADISH H V, OOI B C, TAN K L, et al. IDistance: an adaptive B+-tree based indexing method for nearest neighbor search[J]. ACM Transactions on Database Systems, 2005, 30(2): 364-398. |
| [9] | AUCLAIR A, COHEN L D, VINCENT N. How to use SIFT vectors to analyze an image with database templates[C]//Proceedings of the 5th International Workshop on Adaptive Multimedia Retrieval. Paris, France, 2008: 224-236. |
| [10] | SLANEY M, CASEY M. Locality-sensitive hashing for finding nearest neighbors[J]. IEEE Signal Processing Magazine, 2008, 25(2): 128-131. |
| [11] | 张军旗, 周向东, 王梅, 等. 基于聚类分解的高维度量空间索引B+-tree[J]. 软件学报, 2008, 19(6): 1401-1412.ZHANG Junqi, ZHOU Xiangdong, WANG Mei, et al. Cluster splitting based high dimensional metric space index B+-tree[J]. Journal of Software, 2008, 19(6): 1401-1412. |
| [12] | 杨恒, 王庆, 何周灿. 面向高维图像特征匹配的多次随机子向量量化哈希算法[J]. 计算机辅助设计与图形学学报, 2010, 22(3): 494-502.YANG Heng, WANG Qing, HE Zhoucan. Mutiple randomized sub-vectors quantization hashing for high-dimensional image feature matching[J]. Journal of Computer-Aided Deasign & Computer Graphics, 2010, 22(3): 494-502. |
| [13] | LOWE D. OpenSIFT—An open-source SIFT library.[2013-11-15]. |
| [14] | The Visual Geometry Group. Affine covariant features. (2007-07-15)[2013-11-15]. |



