2. 清华大学 计算机科学与技术系, 北京 100084;
3. 清华大学 智能技术与系统国家重点实验室, 北京 100084
2. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China;
3. State Key Laboratory of Intelligent Technology and System, Tsinghua University, Beijing 100084, China
触觉是一种基本的感觉方式,无论对于人类自身还是机器人,触觉信息都是与周围环境进行交流的重要媒介。人类使用皮肤上的触觉器官来感知物体的温度,合理地抓取物品,并通过触摸来分辨视觉上看似相同但材质不同的物体。对于机器人系统,触觉信息可以帮助机器人完成检查和控制物体摆放位置、识别抓取物体等任务,这对于实现机器人的外部环境探索和对物体的操控,有着极其重要的意义。
迄今为止,人们对机器人感知,包括基于触觉的抓取稳定性、目标分类等方面进行了广泛而深入的研究,特别是人工智能的理论研究方法在机器人领域取得了巨大的成就[1]。文献[2]中对机器人情感描述模型进行了研究。文献[3]描述了安装胡须型触觉传感器的移动机器人进行目标定位和目标抓取的过程。在文献[4]中,作者通过使用灵巧手对大量物体抓取的仿真实验,提供了一个可以对抓取稳定性进行预测的数据集合。文献[5, 6]使用Schunk三指和两指灵巧手对一系列物体进行抓取,并对抓取数据使用隐马尔科夫模型(hidden mark models,HMMs)方法进行处理,实现对抓取稳定性的判断。文献[7]中,作者将自制触觉传感器安装在Schunk二指灵巧手手指两端,对刚性和非刚性物体进行抓取实验,使用触觉信息对抓取物体进行分类。文献[8]使用综合稀疏编码算法(spatio-temporal online recursive kernel Gaussian process,STORK-GP)对5指iCub机器人灵巧手触觉进行采样数据以及目标分类预测和不确定性估计。文献[9]使用神经网络方法对物体的触觉数据进行分类,与文献[10]中使用提取特征来组成模型袋来进行物体的分类有着很大的区别。另外,文献[11]中描述了使用C4.5算法对触觉数据进行处理以实现物体分类。
对触觉信息建模的工具为线性动态系统(linear dynamical system,LDS)[12],该模型使用欧几里德距离作为LDS的距离量度,用于触觉建模。由于LDS并非存在于欧式空间,因此该方法具有较强的局限性。为解决上述问题,本文使用可对LDS进行充分刻画的Martin距离作为量度工具,采用机器学习领域中流行的Bag-of-Words框架对触觉数据进行分析,并且将其与LDS相结合构建了Bag-of-System框架,最后进行实验验证。另外本文构建了由16种实验样本组成的触觉数据集,与国外同类研究中的触觉数据集规模相比有一定优势。
1 触觉序列分类本节将详细描述提取LDS特征、完成码书组建、最终将得到的触觉序列系统包模型与物体标签送入SVM中训练分类器的方法。
1.1 LDS建模基于触觉序列的分类方法是通过局部特征提取以实现全局类别界定,因此,需将触觉序列分为一系列子序列,并对每组子触觉序列进行特征提取。参照文献[13]中的方法对触觉序列进行分段处理,其中子序列分段个数d与窗函数宽度L会影响分类准确率,这将在实验验证部分详细介绍。
众所周知,具有任意协方差的二阶系统可用零均值高斯白噪声驱动的线性动态系统进行建模[14]。对于任意一组子触觉序列y(t),定义其为一组触觉观测序列,并有 ,p为触觉序列维数,t为触觉序列采样时间,使用y(t)进行触觉建模。
,p为触觉序列维数,t为触觉序列采样时间,使用y(t)进行触觉建模。
假设存在正整数n、对称正定矩阵Q∈Rn×n和R∈Rp×p,则有
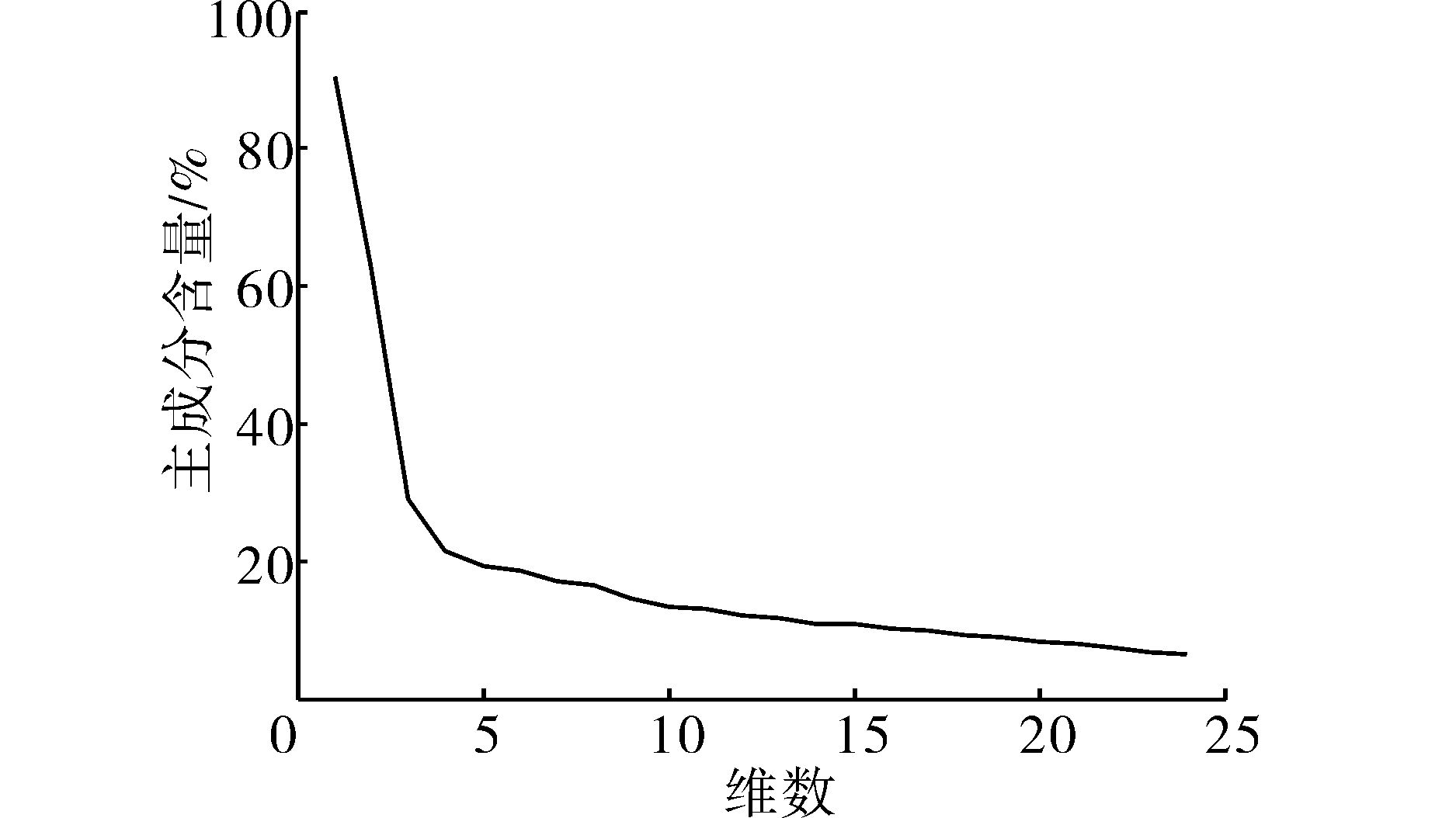
文献[15]中已经验证元组(A,C)可以体现动态序列的时间特性与空间特性,结合文献[12]中基于LDS的建模方法,本文也选用观测序列的元组(A,C)表征动态系统的特性。但由于实验中触觉数据集样本的观测序列的维数p=24较高,上述计算过程会比较复杂,因此对观测序列进行主成分分析(principal component analysis,PCA)降维。由图 1所示的PCA衰减曲线可知,随着维数不断增加,系统主成分含量随之减少,选取主成分含量约为90%时所对应的维数作为降维处理后的维数,即m=5。
|
| 图 1 主成分衰减曲线 Fig. 1 Decaying curve of principle component |
使用奇异值分解(single value decomposition,SVD)对降维处理后的观测序列进行计算:

系统状态参数C与X的估计值为 ,
, =ΣVT,其中,
=ΣVT,其中, ={x(1),x(2),…,x(τ)},
={x(1),x(2),…,x(τ)}, 为t时刻的隐状态序列。
为t时刻的隐状态序列。
使用最小方差法计算隐状态动态矩阵A:
就此完成了触觉序列的特征提取,得到一系列观测矩阵元组(A,C)。但这种特征不能作为特征向量直接送入SVM中训练分类器,还需对其进行后续处理。
1.2 码书组建 1.2.1 马丁距离对于提取的特征存在于欧式空间的分类算法,其特征之间的距离需使用欧式距离来衡量。然而,2组LDS特征M1=(A1,C1)、M2=(A2,C2)存在于非欧式空间中,参照文献[16]中的方法,使用马丁距离来衡量LDS之间的距离。
马丁距离是基于2个系统之间的空间角定义的,这种空间角又称为观测子序列模型参数的规则角(principle angles)。在系统中,即为LDS特征之间的规则角,定义为
 表示特征之间的规则角。
表示特征之间的规则角。
对于任意2个模型之间规则角的计算,首先使用李雅普方程求解P矩阵:
然后使用式(6)计算子空间角{θi}i=1n的余弦值:

使用上述方法进行计算后,得到特征间的马丁距离矩阵:
聚类是码书构建过程中不可或缺的一部分,且聚类中心个数k的选取直接影响数据分类的准确性。K-Means与K-Medoid是2种常用的聚类算法。由于使用K-Means算法需要将上述马丁距离转换为欧式距离后进行运算,而K-Medoid算法可以直接使用马丁距离进行运算,因此,选用K-Medoid算法进行聚类。
K-Medoid算法首先在数据中选取一些点作为聚类中心,剩余的点根据与聚类中心点的距离进行分组。聚类中心可以作为数据平面的中心点,其选取遵循该点与其他数据点的平方距离和最小这一原则,这种距离可以为马丁距离、欧式距离或者其他距离。
使用K-Medoid算法对马丁距离矩阵D进行聚类后,得到由LDS特征组建的码书{Mi}i=1k,其中k为聚类中心个数,每组LDS特征被称为码词(Codeword)。
1.3 系统包模型使用码书对触觉序列表征得到系统包模型{BoS(i)}i=1m。这种表征方式外部体现为直方图模型h=[h1 h2 … hm]T∈Rm,可由特征词频率(term frequency,TF)算法得到。
假设在第i组触觉序列中,第j组码词出现的次数为cij次,则有
经过上述过程,得到触觉序列系统包,它由m组特征向量组成,可与物体标签一起送入SVM中训练分类器。
1.4 分类器设计支持向量机作为一种高准确率的分类工具,被广泛应用于物体识别与分类等领域[17, 18]。SVM分类器既可以直接进行二分类,也可以完成多分类任务。输入SVM中的样本规定为{hi,li}i=1m形式,式中hi为特征向量,li表示第i个特征向量对应标签,m为特征向量个数,也为触觉序列个数。
SVM使用线性核函数{ωTch|c∈ψ}创建一组超平面来完成线性数据二分类,式中ωc为权重向量,也为超平面的法向量,并将分类问题转换为最优化问题:

对于多分类问题,SVM使用+1标记属于该类别的样本,而使用-1进行标记不属于该类别的样本,并采用“一对多”的方法,设置一系列子分类器训练分类器,分别计算各个子分类器的决策函数值,选取最大函数值所对应的类别作为测试数据的标签:

基于核函数的SVM适用于样本非线性的情况。使用径向基核函数(radial basis function,RBF)κ(h1,h2)=exp[-γ×d(h1,h2)]进行数据分类,其中γ为自由参数,d(h1,h2)表示特征向量之间的距离。
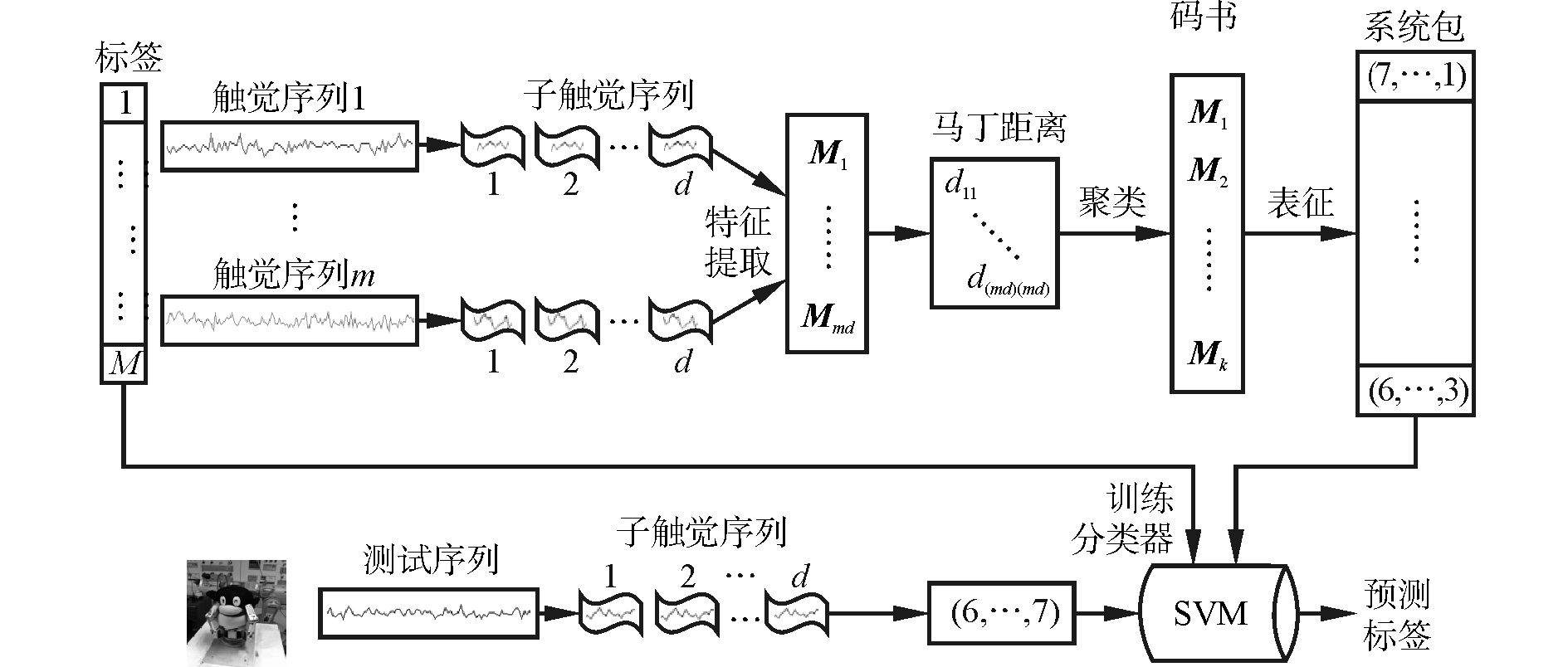
1.5 算法流程如图 2所示,算法流程步骤如下:
|
| 图 2 算法流程 Fig. 2 The work flow of our method |
1)将每组触觉序列分为d组触觉子序列,使用LDS模型对每组子序列进行建模,分别提取子触觉序列的特征M。
2)使用马丁距离计算动态特征之间的距离,并使用K-Medoid算法进行聚类,组建码书。
3)使用码书对每组触觉序列进行表征,得到每组触觉序列的字典(bag-of-word,BoW),所有字典组成“系统包”(bag-of-system,BoS)模型。
4)将系统包与物体标签一起送入SVM训练分类器。
5)对测试序列进行分类预测时,重复上述过程,送入分类器即可得到物体的标签。
2 实验结果与分析 2.1 数据采集实验使用BH8-280三指灵巧手对16种日常用品进行抓取。如图 3所示,实验物品分别为橙色圆筒、咖啡杯、可乐瓶、瓦力玩具、粉色杯子、企鹅玩偶、熊猫玩偶、塑料三角、透明圆筒、灰色圆筒、红纸盒、白色纸筒、金色海绵圆筒、褐色海绵圆筒、牛奶盒和金色海绵块。

|
| 图 3 实验物品 Fig. 3 Experiment objects |
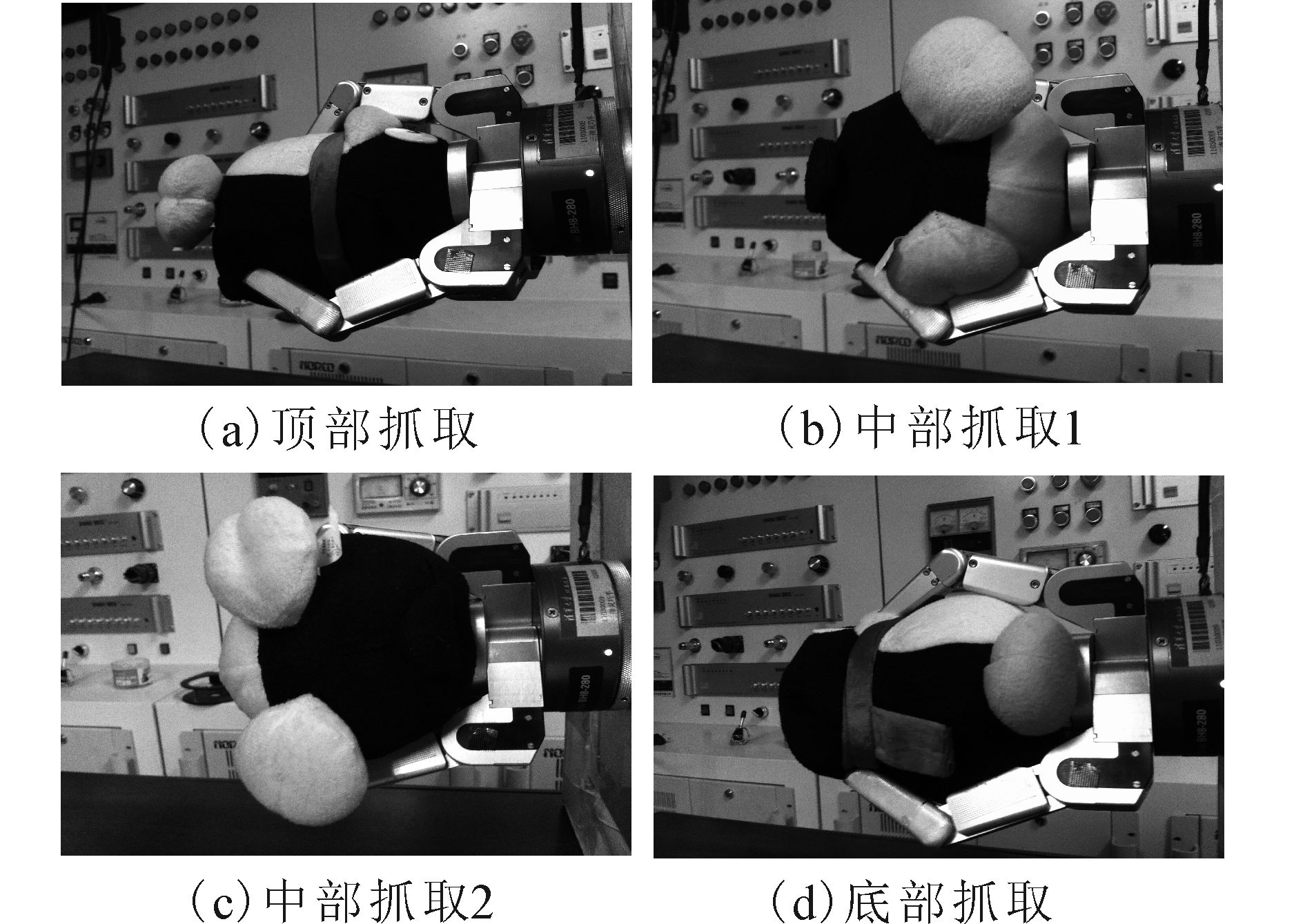
对于每一种实验物体,进行50次抓取实验,抓取方式参照文献[12],灵巧手手掌分别与物体上部、中部和底部的不同部位进行接触。图 4为企鹅玩偶与灵巧手手掌接触方式示意图。
|
| 图 4 抓取位姿 Fig. 4 Grasping poses |
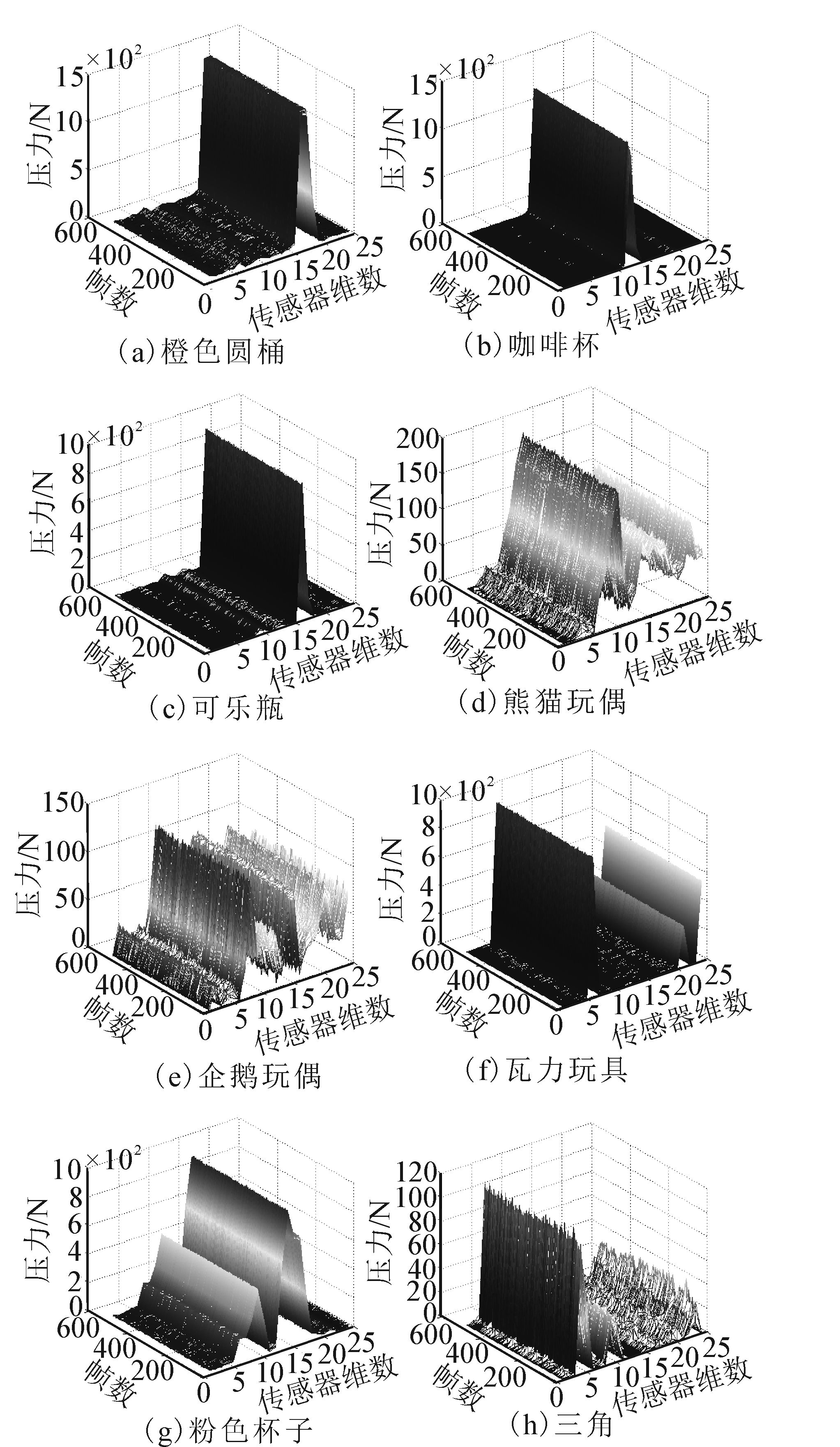
手掌在抓取不同物体时,实验物体的材质、形状等物理信息会使触觉信息产生差异,这种差异可以作为物体识别和分类的依据[19]。选取8种物体的触觉序列进行触觉图像绘制,如图 5所示,不同物体的抓取图像有明显差异。
|
| 图 5 触觉图像 Fig. 5 Tactile images |
对触觉序列进行数据处理,选取稳定阶段的触觉序列进行分析,将每组样本长度限定为500个样本点(采样时间50 s),得到800组样本长度为500的触觉序列样本。对于每种物体的50组样本,随机选取30组样本作为训练集,剩余20组作为测试集,共计480组训练集样本,320组测试集样本。
2.2 分类结果如前所述,以下因素会对分类准确率造成影响:子触觉序列分段个数d、窗函数宽度L、聚类中心数k以及SVM的参数C、γ。
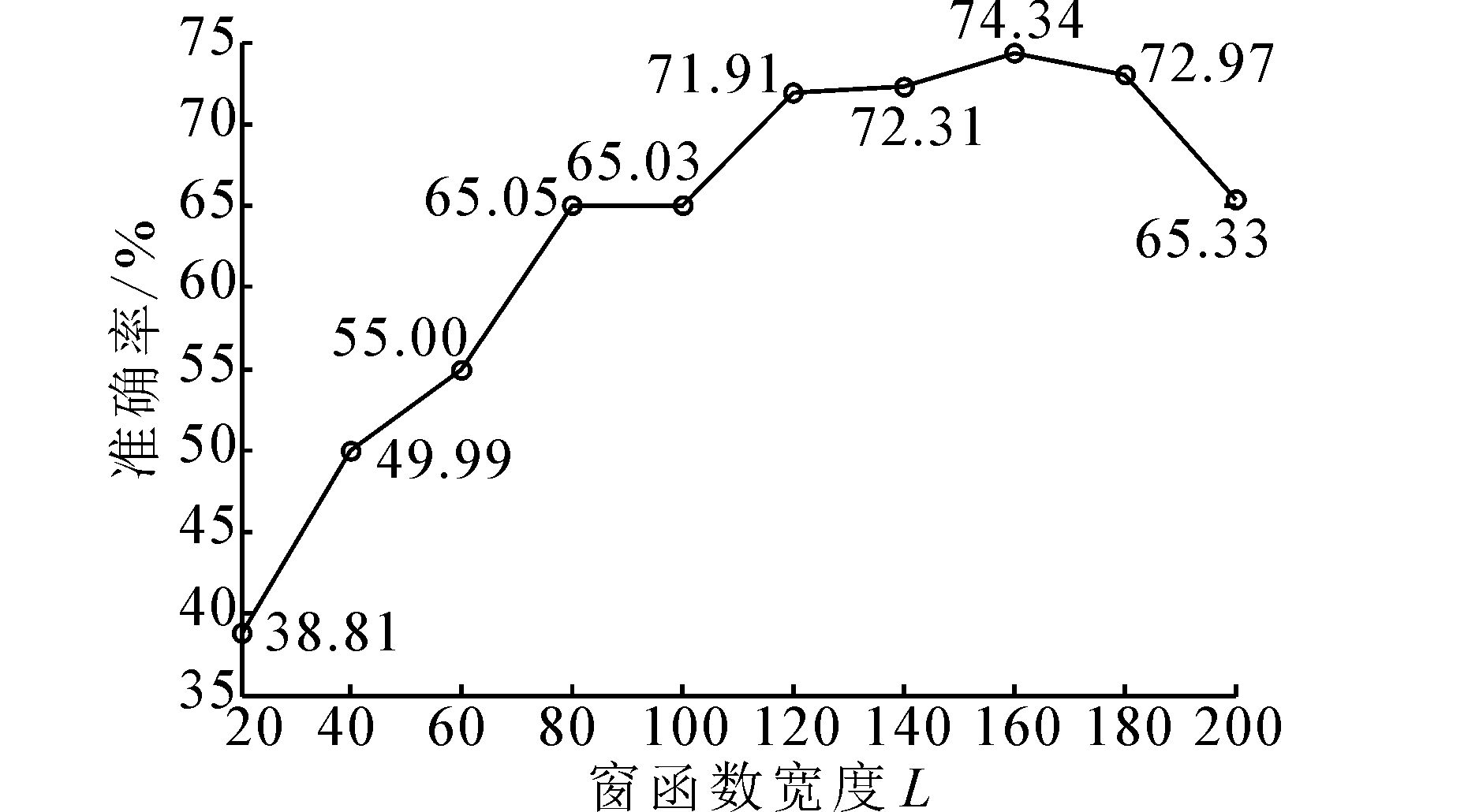
首先,其余参数固定不变,使用网格法对SVM的参数进行调节,记录最优准确率下的C、γ参数,在后续参数调节过程中,C、γ参数固定不变。凭经验值选取d值,选取原则为每段子序列中包含尽量完整的特征。确定子序列分段个数d后,继续改变窗函数宽度L,并记录不同窗宽下的准确率。由于测试集样本为随机选取,为了减小样本之间的差异,对每组窗宽的取值进行10次实验,对准确率求取平均值,最终选定L=160。图 6为不同窗宽L下的准确率曲线。
|
| 图 6 不同窗宽L的准确率曲线 Fig. 6 Accuracy curves under different value of L |
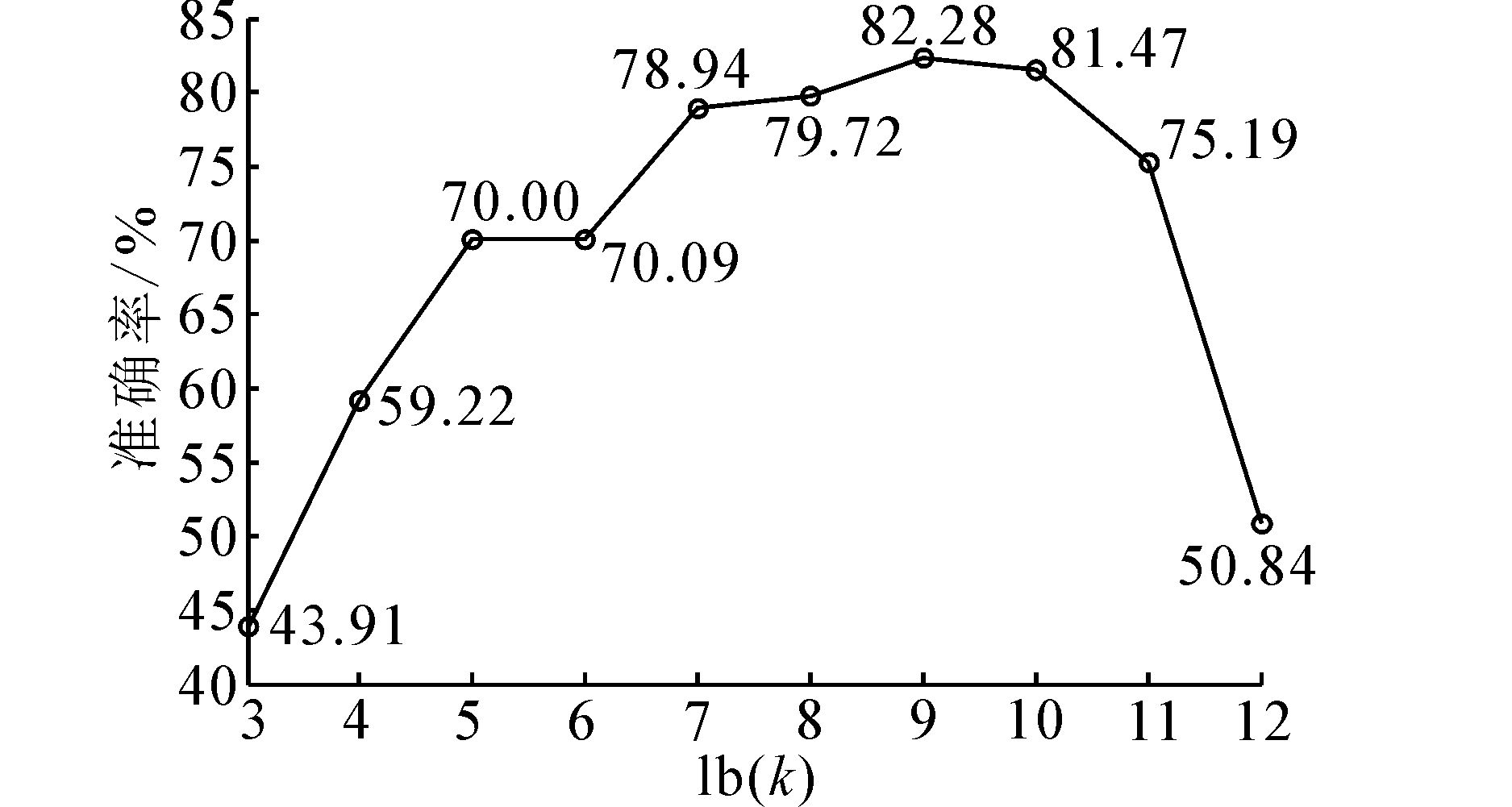
在L=160,C、γ最优条件下,以{2j}j=312递增形式选取8~4 096之间10个值作为聚类中心个数k。每组k值进行10组实验,对准确率取平均值。由图 7可知,随聚类点数量增加,分类准确率呈上升趋势,并且在k=512时达到最大值82.28%。但是,随着聚类中心点的继续增加,准确率开始下降。这是由于聚类中心过多导致特征描述过细,使相似的LDS特征被误分。
|
| 图 7 不同k值下的准确率曲线 Fig. 7 Accuracy curves under different value of k |
为了直观显示本算法对各物体的识别能力,绘制了最优分类时的混淆矩阵。如图 8所示,可以看出该算法可以较好地实现物体的分类。

|
| 图 8 SVM最优分类混淆矩阵 Fig. 8 Confusion matrix of SVM at best accuracy |
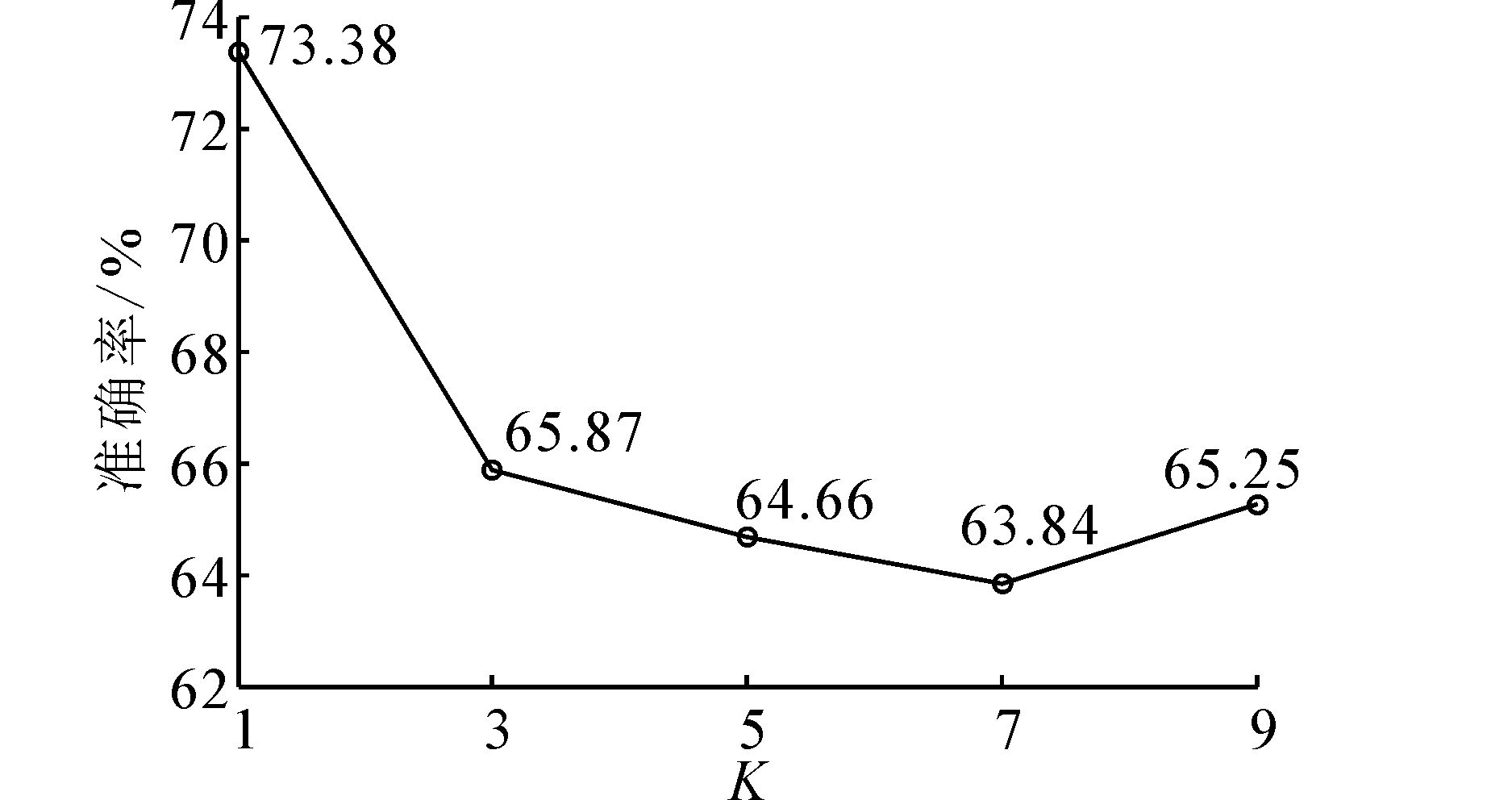
为与文献[12]中的K-NN方法进行对比,本文使用K-NN算法对数据进行处理。使用相同的训练集与测试集数据来保证实验的可比性,并对稳定抓取阶段整体触觉序列进行建模后使用K-NN算法训练分类器。图 9为K=1,3,5,7,9时的分类准确率曲线,每组K值进行10次实验,准确率取平均值。在1-NN时,分类准确率达到最大值73.38%,同时绘制了此时的混淆矩阵,如图 10所示。
|
| 图 9 不同K值下的准确率曲线 Fig. 9 Accuracy curves under different value of K |

|
| 图 10 1-NN算法最优分类混淆矩阵 Fig. 10 Confusion matrix of 1-NN at best accuracy |
对比上述2种分类方法的混淆矩阵,可以发现本文提出的算法进行数据分类时,橙色圆筒、熊猫玩偶、白色纸筒等物体的识别率普遍高于K-NN算法,但是透明圆筒、灰色圆筒的识别率略有下降。这可能由于聚类过程中,这些实验物体的部分特征与其他物体的特征的距离较近而被误分。但从整体分类情况看,本文算法优势明显。
3 结束语本文使用灵巧手手掌稳定抓取阶段的触觉数据完成LDS触觉建模。对于随机选择的训练集样本,进行特征提取等处理后得到系统包模型,并与物体标签一起送入SVM中训练分类器实现物体分类。由LDS组建的系统包模型相较于单一的LDS特征可以更有效地捕捉触觉序列的时空特征,且建模方便,但由于特征存在于非欧式空间中,因此选用马丁距离进行距离衡量,但过程相对耗时。对比SVM和1-NN 2种分类方法的准确率曲线及混淆矩阵可知,SVM分类方法优势明显。在今后的研究中,希望将此分类方法与机器人实时抓取任务相结合,在机器人抓取过程中进行物体类别的判定,实现灵巧抓取。
| [1] | 李德毅. 网络时代人工智能研究与发展[J]. 智能系统学报, 2009, 4(1): 1-6. LI Deyi. AI research and development in the network age [J]. CAAI Transactions on Intelligent Systems, 2009, 4(1): 1-6. |
| [2] | 解仑, 王志良, 余军. 人工心理情感模型的个人机器人[J]. 智能系统学报, 2009, 4(1): 59-66. XIE Lun, WANG Zhiliang, YU Jun. A personal robot based on an affective model of artificial psychology[J]. CAAI Transactions on Intelligent Systems, 2009, 4(1): 59-66. |
| [3] | RUSSELL R A, WIJAYA J A. Object location and recognition using whisker sensors[C]//Australian Conference on Robotics and Automation. Brisbane, Australia, 2003: 761-768. |
| [4] | GOLDFEDER C, CIOCARLIE M, DANG H, et al. The Columbia grasp database[C]//IEEE International Conference on Robotics and Automation. Kobe, Japan, 2009: 1710-1716. |
| [5] | BEKIROGLU Y, LAAKSONEN J, JORGENSEN J, et al. Assessing grasp stability based on learning and haptic data[J]. IEEE Transactions on Robotics, 2011, 27(3): 616-629. |
| [6] | BEKIROGLU Y, KRAGIC D, KYRKI V. Learning grasp stability based on tactile data and HMMs[C]//IEEE International Symposium on Robot ad Human Interactive Communication. Viareggio, Italy, 2010: 132-137. |
| [7] | DRIMUS A, KOOTSTRA G, BILBERG A, et al. Design of a flexible tactile sensor for classification of rigid and deformable objects[J]. Robotics and Autonomous Systems, 2014, 62(1): 3-15. |
| [8] | SOH H, SU Y Y, DEMIRIS Y. Online spatio-temporal Gaussian process experts with application to tactile classification[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura, Portugal, 2012: 4489-4496. |
| [9] | JIMÉNEZA A, SOEMBAGIJOB A, REYNAERTSB D, et al. Featureless classification of tactile contacts in a gripper using neural networks[J]. Sensors and Actuators A: Physical, 1997, 62(1/2/3): 488-491. |
| [10] | SCHNEIDER A, STURM J, STACHNISS C, et al. Object identification with tactile sensors using bag-of-features[C]//IEEE/RSJ International Conference on Intelligent Robot Systems. St Louis, USA, 2009: 243-248. |
| [11] | SCHOPFER M, PARDOWITZ M, HASCHKE R, et al. Identifying relevant tactile features for object identification[M]//PRASSLER E, ZÖLLNER M, BISCHOFF R. Towards Service Robots for Everyday Environments. Berlin/Heidelberg: Springer, 2012: 417-430. |
| [12] | 萧伟, 孙富春, 刘华平. 机器人灵巧手的触觉分析与建模[J]. 机器人, 2013, 35(4): 394-401. XIAO Wei, SUN Fuchun, LIU Huaping. Tactile analysis and modeling of dexterous robotic hand[J]. Robot, 2013, 35(4): 394-401. |
| [13] | BAYDOGAN M G, RUNGER G, TUV E. A bag-of-features framework to classify time series[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2796-2802. |
| [14] | DORETTO G, CHIUSO A, WU Y N, et al. Dynamic textures[J]. International Journal of Computer Vision, 2003, 51(2): 91-109. |
| [15] | RAVICHANDRAN A, CHAUDHRY R, VIDAL R. Categorizing dynamic textures using a bag of dynamical systems[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(2): 342-353. |
| [16] | De COCK K, De MOOR B. Subspace angles between ARMA models[J]. Systems & Control Letters, 2002, 46(4): 265-270. |
| [17] | WANG W, LIU H P, YU L Z, et al. Human activity recognition using smart phone embedded sensors: a linear dynamical systems method[C]//2014 International Joint Conference on Neural Networks (IJCNN). Beijing, China, 2014: 1185-1190. |
| [18] | 赵春晖, 陈万海, 郭春燕. 多类支持向量机方法的研究现状与分析[J]. 智能系统学报, 2007, 2(2): 11-17. ZHAO Chunhui, CHEN Wanhai, GUO Chunyan. Research and analysis of methods for multiclass support vector machines[J]. CAAI Transactions on Intelligent Systems, 2007, 2(2): 11-17. |
| [19] | CHITTA S, STURM J, PICCOLI M, et al. Tactile sensing for mobile manipulation[J]. IEEE Transactions on Robotics, 2011, 27(3): 558-568. |



