2. 北京航空航天大学 计算机学院, 北京 100083
2. School of Computer Science and Engineering, Beihang University, Beijing 100083, China
迅速有效地诊断出一个复杂系统的故障是所有过程专家和现场工作人员的主要目的之一。这一举措不仅能提高产量,提升经济效益,还能降低事故发生的风险。目前已有许多学者提出了不同故障诊断的方法。大体来讲,这些方法可分为3类:基于知识的方法、基于模型的方法以及基于数据驱动的方法。像专家系统、模糊逻辑这些基于知识的方法[1],是利用根据系统特性建立的定性模型。基于模型的方法,例如状态估计法及参数估计法[2, 3, 4],是根据系统内的物理关系来组建系统的分析模型。一些基于数据驱动的方法,比如神经网络(ANN)[5-6]或者主元分析法(PCA)[7],是利用历史过程数据统计进行数学分析。上述提到的各种方法都已广泛应用到了各个领域。它们都有各自的优缺点,基于知识的方法比较依赖于专家的知识,而一些基于数据驱动的方法则需要大规模的历史数据才能得到比较准确的结果。因此近些年,多种故障诊断方法的结合算法被应用到各种过程中[8, 9, 10, 11]。
动态不确定因果图(dynamic uncertain causality graph,DUCG)是一种结合了定性模型与定量概率推理的新系统。这一方法根据知识来建立模型并根据严格的概率论来计算故障的概率,避免了单一定性或定量方法的缺陷。DUCG实现了不确定因果知识的简洁(compact)表达,并提供了有效的概率推理,使推理结果可以解释。作为一种新的知识表达与推理方法,DUCG已经应用到了医药领域[12]及核电领域[13]。
本文旨在证明DUCG是一种可以有效诊断化工系统故障的方法,在文献[14]的研究基础上,进一步完善了DUCG知识库的内容,使诊断结果更加准确,文献[14]中未能模拟并诊断的故障16在本文中得到了准确诊断;同时针对原DUCG系统在震荡型故障上诊断的不足,用新方法给出了改进的数据发送模块,调整了DUCG知识库建模,并取得了更理想的结果。
1 动态不确定因果图 1.1 DUCG简介DUCG是一个可以包含环路的有向图,图 1展示了DUCG所应用的一些标准符号,这些符号的定义如下。
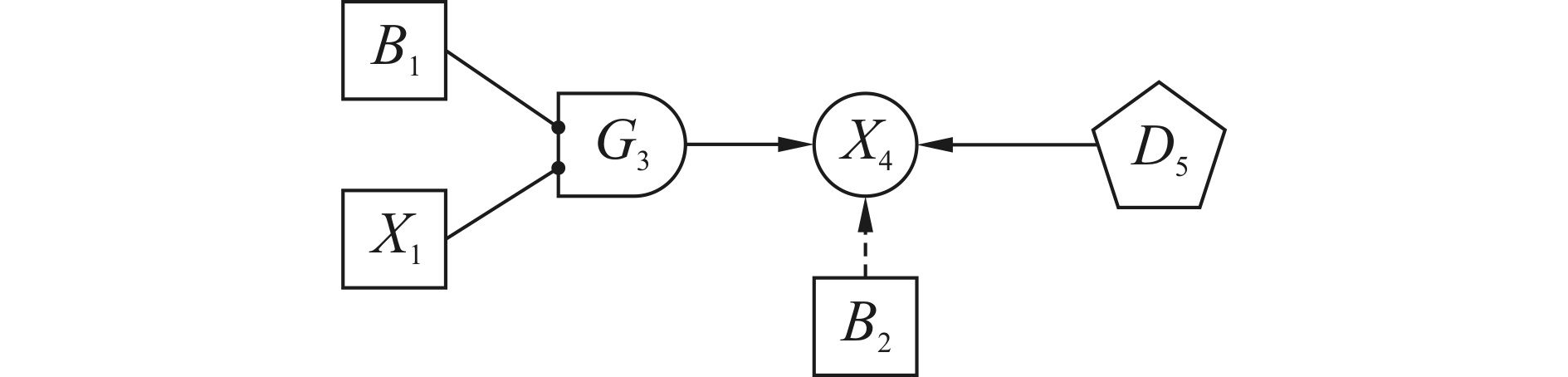
|
| 图 1 DUCG示例 Fig. 1 Illustration for DUCG |
Bi是DUCG中的基本变量(根变量),i为变量标号,Bij为Bi处于j状态的事件。B类型变量(事件)只有输出,没有输入,在图中用矩形表示。
Xn是DUCG中的结果或效果变量,在图中用圆形表示,n为变量标号。Xnk为Xn处于k状态的事件。
Gn是DUCG中的逻辑门变量,至少有2个输入,1个输出,Gnk为Gn处于k状态的事件。逻辑门把其输入变量各状态的某种逻辑组合作为其一个状态,从而使DUCG的表达更加简洁。
Dn是DUCG中的缺省事件,代表Xn的未知原因,用五边形表示。
实箭头表示连接变量,写为Fn;i,是原因变量Vi(V∈{B,X,G,D})作用于结果变量Xn的作用变量。由于Vi和Xn有不同状态,Fn;i是一个矩阵,由Fnk;ij组成。Pr{Fnk;ij}=(rn;i/rn)Pr{Ank;ij}=(rn;i/rn)ank;ij,其中Ank;ij代表Vij导致Xnk发生这一虚拟的因果作用事件,其发生概率为ank;ij,rn;i>0为Vi和Xn之间存在因果关系的关联度,rn=∑irn,i。
虚箭头表示条件作用变量,即仅当条件Zn;i满足时,Fn;i才成立,否则Fn;i被删除。
1.2 DUCG的概率推理DUCG的概率推理基于如下假设:
假设Vi是Xn的父变量,那么有
DUCG概率推理的第1项工作是根据接收到的证据对DUCG进行化简。当DUCG接收到了证据信息E(通常为一组X变量的状态事件),就可以通过证据信息E中观测到的X变量的非正常状态实现DUCG的化简:不可能存在及无意义的变量和因果关系将在推理过程中被删除。化简的规则和细节详见参考文献[15],这些化简规则可以反复任意顺序使用直至DUCG无法继续化简。化简DUCG,不仅可以迅速找到问题区间,还可以在保证计算精确度的同时,大幅降低计算规模。
接下来第2项工作是对E中的事件按照式(1)进行逻辑展开,用以计算Pr{Hkj|E}=Pr{HkjE}/Pr{E},其中Hkj为待求的假设事件,亦即故障事件,通常为B类型事件,仅存于化简后的DUCG中。展开HkjE和E的方法相同,详见参考文献[15]。在展开的表达式中,只有F和B类型事件,将其发生概率代入即可计算Hkj的验后概率。
Hkj的状态概率定义为hkjs≡Pr{Hkj|E}、排序概率定义为 。其中SH为存在于化简DUCG中的所有可能故障假设的集合。当SH中只有1个Hkj时,无需计算即可知hrkj=1(100%)。
。其中SH为存在于化简DUCG中的所有可能故障假设的集合。当SH中只有1个Hkj时,无需计算即可知hrkj=1(100%)。
对于动态故障诊断,DUCG目前采用的方法是假定各时间片ti内的化简DUCG均包含待求故障假设Hkj,且证据E(ti)在给定Hkj的条件下独立,则用式(2)进行计算:
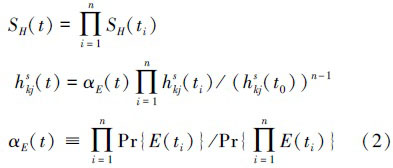
为了验证DUCG在故障诊断上的有效性,采用了Tennessee Eastman(TE)过程作为诊断的实例。TE过程是由Tennessee Eastman公司设计的实际工业过程的仿真模拟,旨在开发、研究及评价过程控制理论和技术。Ricker针对这一过程编译了matlab的仿真程序。本文采用了Ricker提供的程序,该TE过程的工艺流程图及采用的控制回路如图 2所示。
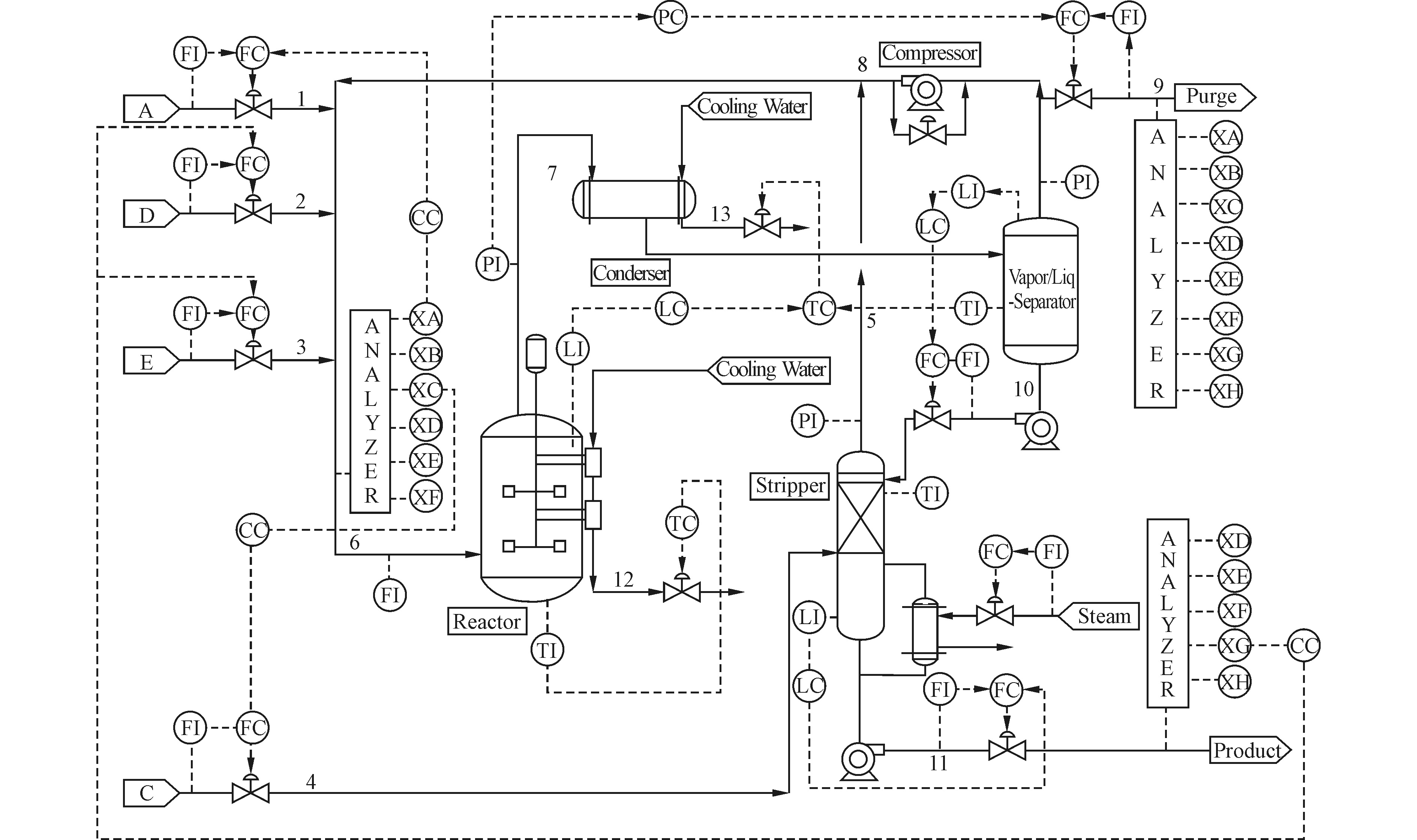
|
| 图 2 TE过程工艺流程 Fig. 2 The Tennessee Eastman process |
TE过程由5个主要单元组成:反应器、冷凝器、汽提塔,气液分离装置及压缩机;TE的生产过程包含4种气态的起始反应物:A、C、D、E,每种起始反应物都混有1%的惰性气体B,它们被喂入反应器后会生成2种气态产物G和H,同时会生成液态副产物F。该过程包含了41个观测变量、12个操作变量以及20个故障(见表 1)。故障1至故障8为数据阶跃变化的故障;故障9至故障12为数据随机变化的故障;故障13是反应动力学缓慢漂移;故障14和15为数据称震荡趋势的阀门粘滞故障;故障16至故障20为未知故障。TE过程被广泛的应用到各种不同研究领域来测试各种理论的实际效果。在故障诊断领域,像PCA、贝叶斯网络(BN)等理论已经通过TE过程证明了其有效性。在本文中,TE过程也用于验证DUCG理论的有效性,基于不同的故障,TE过程的故障数据不仅可以当作离线数据来建立DUCG模型,同时可以仿真成实时数据来验证DUCG的实时性。
| No. | 故障 | 故障类型 |
| 1 | A/C进料比变化,B组分不变 | 阶跃 |
| 2 | B组分变化,A/C组分不变 | 阶跃 |
| 3 | 物料D温度 | 阶跃 |
| 4 | 反应器冷却水温度 | 阶跃 |
| 5 | 冷凝器冷却水温度 | 阶跃 |
| 6 | 物料A损失 | 阶跃 |
| 7 | 物料C压头损失 | 阶跃 |
| 8 | A、B、C组分 | 随机 |
| 9 | 物料D温度 | 随机 |
| 10 | 物料C温度 | 随机 |
| 11 | 反应器冷却水温度 | 随机 |
| 12 | 冷凝器冷却水温度 | 随机 |
| 13 | 反应器反应动力学 | 缓慢漂移 |
| 14 | 反应器冷却水阀门 | 粘滞 |
| 15 | 冷凝器冷却水阀门 | 粘滞 |
| 16 | 未知 | — |
| 17 | 未知 | — |
| 18 | 未知 | — |
| 19 | 未知 | — |
| 20 | 未知 | — |
要应用DUCG理论,首先要建立过程的DUCG知识库。知识库的建立步骤如下:
1)根据目标过程建立变量列表,在TE过程中,故障被定义成B型变量,观测变量和操作变量被定义成X型变量。
2)对B型及X型变量进行状态划分。
3)定义B型变量的先验概率参数。
4)根据专家经验建立子DUCG。
5)通过计算机将所有子DUCG合成,形成完整的DUCG知识库。
根据上述步骤,所建立的TE过程的知识库模型如图 3所示。在这一TE过程的知识库中,一共选取了54个变量。其中有20个B型变量作为根变量,既TE过程的20个故障;还有由25个观测变量和9个操作变量组成的34个X型变量,通过这34个变量可以清晰地观测到所有故障的传递过程。
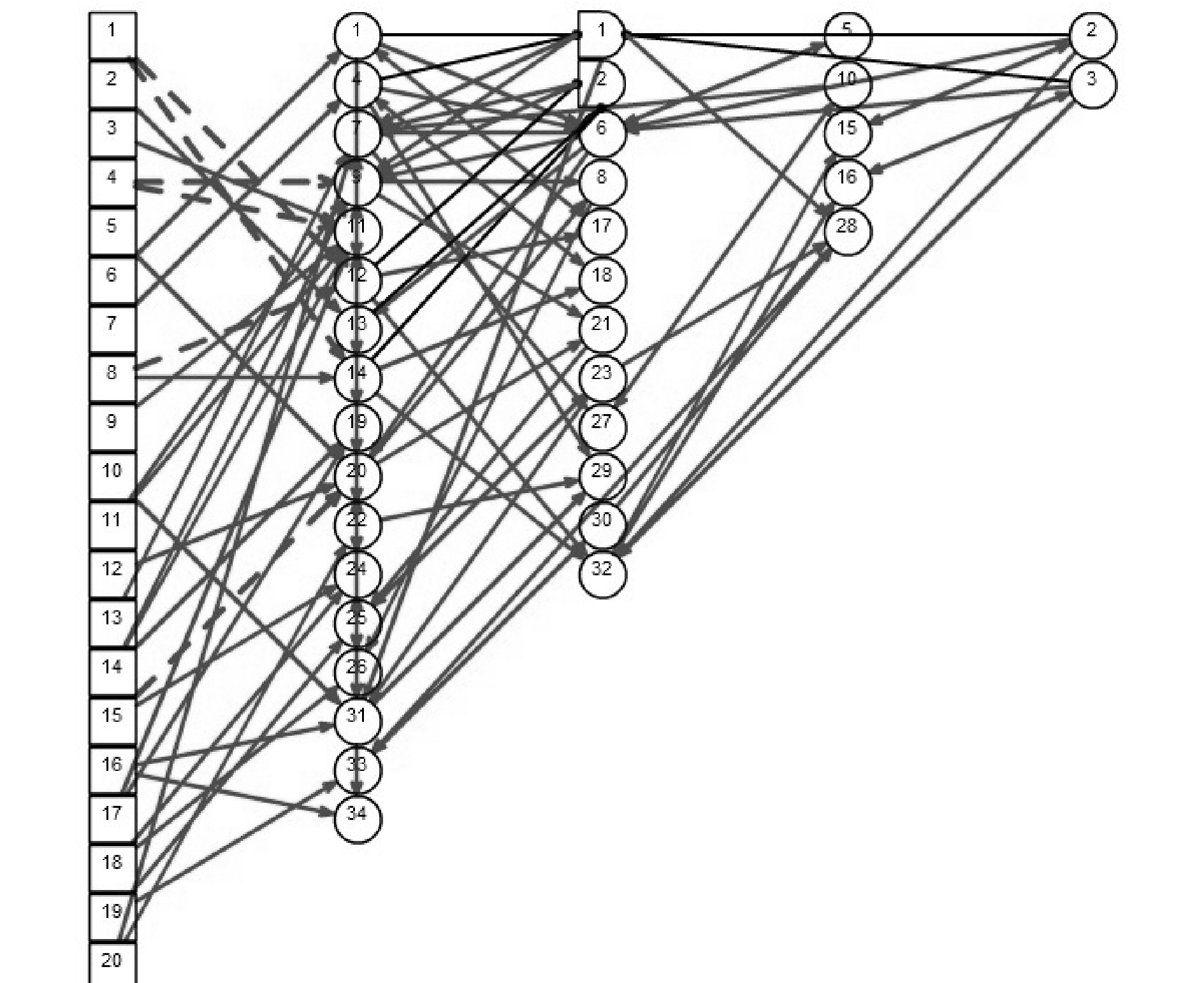
|
| 图 3 TE过程知识库 Fig. 3 The knowledge base of TE process |
与文献[14]建立的知识库相比,本知识库引入了变量X34,使原先无法诊断出的故障16得出了良好的诊断结果,并对知识库的其他连接事件及连接强度进行了重新计算与调整。表 2列出了34个X型变量的详细信息。
本文没有使用到子DUCG(当然可以根据不同的分类建立子DUCG),但是在大规模的系统中,子DUCG的存在就是十分必要的了。
| No. | 变量名 | No. | 变量名 |
| 1 | 物料A进料流量 | 18 | 物料C阀门 |
| 2 | 物料D进料流量 | 19 | 反应器冷却水阀门 |
| 3 | 物料E进料流量 | 20 | 气液分离器温度 |
| 4 | 物料A/C进料流量 | 21 | 气液分离器液位 |
| 5 | 回流量 | 22 | 气液分离器压力 |
| 6 | 反应器进料流量 | 23 | 气液分离器出口流量 |
| 7 | 反应器压力 | 24 | 气液分离器冷却水温度 |
| 8 | 反应器液位 | 25 | 气液分离器阀门 |
| 9 | 反应器温度 | 26 | 冷凝器冷却水阀门 |
| 10 | 放空率 | 27 | 放空阀 |
| 11 | 反应器冷却水温度 | 28 | 汽提塔液位 |
| 12 | 反应器A组分含量 | 29 | 汽提塔压力 |
| 13 | 反应器B组分含量 | 30 | 汽提塔出口流量 |
| 14 | 反应器C组分含量 | 31 | 汽提塔温度 |
| 15 | 物料D阀门 | 32 | 产品中G组分含量 |
| 16 | 物料E阀门 | 33 | 汽提塔阀门 |
| 17 | 物料A阀门 | 34 | 汽提塔蒸汽流量 |
由于TE过程故障较多,本文只列举了几个典型的故障进行详细的讲述。
TE过程的一个典型故障时A/C进料比发生变化、B组分不变(故障1),该故障类型为阶跃。从故障数据可以观测到该故障的异常状态为E=X1,2X7,2X9,1X10,2X12,1X14,2X17,2X18,1X22,2X27,2X29,2,其他X型变量的状态是正常的。当这些异常状态的信号被输入到DUCG后,DUCG的推理机将开始工作,所有不相关或无意义的变量和因果关系都从DUCG中删除。图 4展示了故障1的推理结果。在图 4中,浅灰色表示变量的状态为高,深灰色表示变量的状态为低(不同颜色代表的不同状态可以查阅DUCG的变量列表),从图中可以很容易地理解故障1的推理结果。
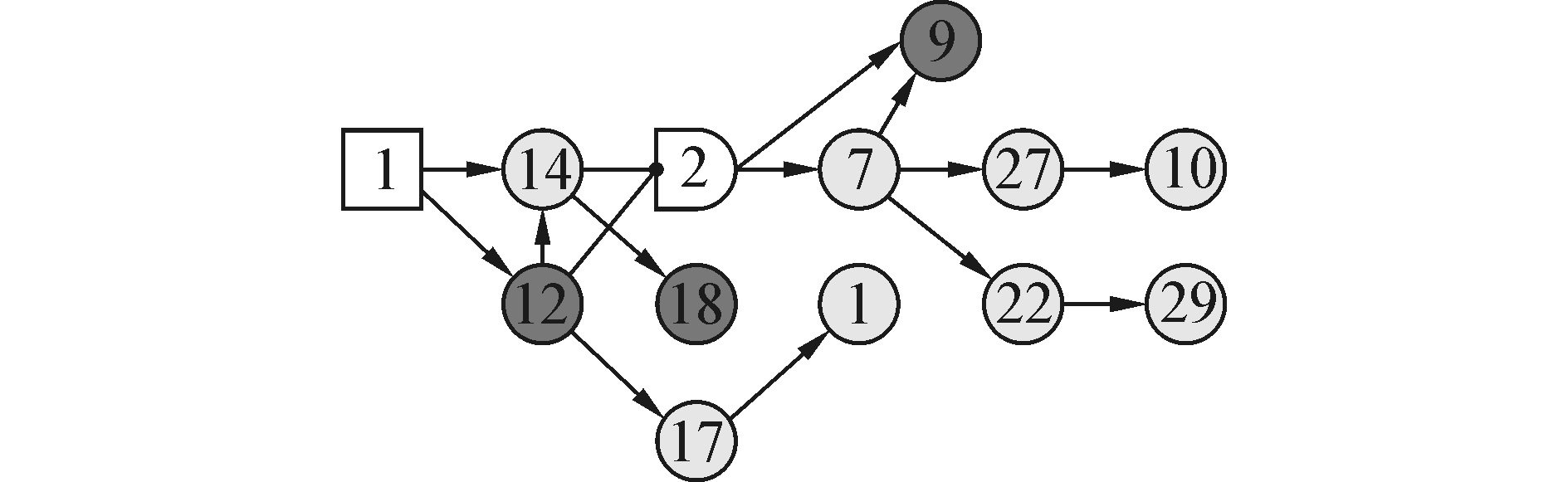
|
| 图 4 故障诊断结果 Fig. 4 The diagnosis result of TE process |
故障诊断的推理结果和预计一样是正确的,因为只有B1能引起所有图中的异常状态。由于推理结果中只有一个B型变量,B1是根据观测到的证据所得到的惟一结果,B变量的先验概率及作用强度都可以忽略。
3.3 震荡型故障的处理方法TE过程的另一典型故障是反应器冷却水阀门粘滞(故障14),该故障的故障数据呈震荡趋势。由于原DUCG的采用的是只保留异常变量的初始状态这一方法,在处理化工过程普遍存在的震荡型故障存在着一些不足,无法准确推理出震荡故障的结果。针对这一问题,本文对数据发送模块重新进行了编译,采用了五点计数法、将震荡当作一个异常状态来处理,使诊断结果更加准确,更适用于化工系统。该方法设置检测到变量的状态为高的次数为a,检测到变量的状态的低的次数为b,当a+b=5时,则令变量状态发送模块发送出震荡状态。从最初的故障数据可以观测到故障的异常状态为X9,1、X11,1、X19,1,其余的变量和因果关系被删除,经过一段时间后,震荡状态被检测出来,故障的异常状态更新为X9,5、 X11,5、 X19,5,并输入到DUCG中得到新的诊断结果。此方法不仅适用于处理震荡故障,同时也可以处理阶跃等各种类型的故障。图 5展示了采用不同的处理方法对故障14的诊断结果。图 5 (a)为采用原始方法得出的诊断结果,排序概率仅为1.23%,图 5 (b)为采用新方法得出的诊断结果,排序概率已达100%。从图中可以明显发现,新的处理方法诊断的结果更加准确。
|
| 图 5 故障14的诊断结果 Fig. 5 The fault diagnosis result of fault 14 |
DUCG可以清晰地描述故障的传递过程,如图 6所示。在t1时刻,DUCG接收到了异常状态X14,2 和 X12,1;根据这2个异常状态,推理机给出了如图 6 (a)的推理结果:B1。当这2个状态引起异常状态X7,2发生并输入到推理机后,DUCG转变成图 6 (b)所示的推理结果。随着时间的进一步推移,DUCG的推理结果也如图 6 (c)~6(g)一样逐步展开,图 6 (g)便为包含了所有异常状态的最终展开结果。

|
| 图 6 故障14的诊断结果 Fig. 6 The fault diagnosis result of fault 14 |
DUCG不仅能展示故障随着时间的发展逐步展开的过程,随着更多证据的输入,DUCG推理出的结果也越来越精确。由于故障1具有唯一的推理结果,这一过程未在上述结果中体现出来。因此图 7中故障14的推理过程展示了推理结果随证据增加更加精确的过程。在震荡过程被检测到之前,由于在故障初始B11与B14具有相同的故障特征,推理机给出的推理结果为B11,诊断概率如图 7 (a)所示仅为0.4%,随着更多证据的输入,震荡状态被检测出来并输入到推理机,诊断概率就如图 7 (d)所示上升至100%。
|
| 图 7 故障14的传递过程 Fig. 7 The transfer process of fault 14 |
DUCG在知识不完备的情况下也可取得良好的诊断结果。TE过程的故障16为未知故障,其排序概率如图 8所示,也达到了100%。
|
| 图 8 故障16诊断结果 Fig. 8 The fault diagnosis result of fault 16 |
不仅是上述3个故障,其余的17个故障也取得了不错的诊断结果,所有故障的排序概率如表 3所示。
| 故障序号 | 排序概率/% | 故障序号 | 排序概率/% |
| 1 | 100 | 11 | 96.85 |
| 2 | 100 | 12 | 100 |
| 3 | 94.77 | 13 | 100 |
| 4 | 97.28 | 14 | 100 |
| 5 | 80 | 15 | 100 |
| 6 | 100 | 16 | 100 |
| 7 | 100 | 17 | 99.32 |
| 8 | 100 | 18 | 100 |
| 9 | 94.97 | 19 | 100 |
| 10 | 100 | 20 | 100 |
| 故障序号 | 诊断正确概率/% | |
| DUCG | BN | |
| 1 | 100 | 97.5 |
| 2 | 100 | 98.12 |
| 3 | 100 | 22 |
| 4 | 100 | 82.37 |
| 5 | 100 | 98 |
| 6 | 100 | 100 |
| 7 | 100 | 100 |
| 8 | 100 | 97 |
| 9 | 100 | 22.62 |
| 10 | 100 | 86.87 |
| 11 | 100 | 75.5 |
| 12 | 100 | 98.25 |
| 13 | 100 | 76.12 |
| 14 | 100 | 98.75 |
| 15 | 100 | 23.5 |
| 16 | 100 | 80.62 |
| 17 | 100 | 85 |
| 18 | 100 | 68.5 |
| 19 | 100 | 96.12 |
| 20 | 100 | 87.37 |
每一个故障的排序概率为该故障数据的概率分布,一般情况下,可以认为正确故障的概率分布大于50%时(排在第一位),则诊断结果正确。所有故障诊断结果与贝叶斯网络诊断结果[16]对比如表 4所示。从结果看出DUCG针对20个故障的诊断都取得了正确的结果,所有故障的排序概率均高于50%,诊断正确概率均达到100%;与贝叶斯网络诊断结果相比,DUCG诊断正确概率都要优于贝叶斯网络,尤其是故障3、9、15及18的诊断结果,DUCG要远远优于贝叶斯网络。
4 结束语本文将DUCG用于化工系统的故障诊断,以TE过程作为实验对象,针对化工系统特性重新编译了DUCG数据发送模块,调整构建了包含54个变量的TE过程知识库,并取得了不错的故障诊断效果。
通过分析实验结果,可以发现DUCG理论在故障诊断领域的优势:1)DUCG可以随着时间的变化而变化,清晰地展示故障的传递过程。2)DUCG可以实现实时的故障诊断,其实时性对实际的化工过程有着重要的意义。3)可以将系统拆分由不同的领域专家建立子DUCG,这样不仅有助于简化大型复杂系统的建立,同时也使构建的DUCG系统更加精确。作为一种基于知识的理论,DUCG也存在着一些缺点,例如依赖于专家知识等。目前DUCG动态诊断方法基于每个时间片的化简DUCG都包含真实故障的假设。这对建造DUCG知识库提出了很高的要求。针对这一缺点,一种新的称为立体DUCG的算法正在开发当中。
| [1] | ABDULGHAFOUR M, EL-GANAL M A. A fuzzy logic system for analog fault diagnosis[C]//1996 IEEE International Symposium on Circuits and Systems. Atlanta, USA, 1996: 97-100. |
| [2] | ICHALAL D, MARX B, RAGOT J, et al. An approach for the state estimation of Takagi-Sugeno models and application to sensor fault diagnosis[C]//Proceedings of the 48th IEEE Conference on Decision and Control, Jointly with the 28th Chinese Control Conference. Shanghai, China, 2009: 7789-7794. |
| [3] | BACHIR S, TNANI S, TRIGEASSOU J C, et al. Diagnosis by parameter estimation of stator and rotor faults occurring in induction machines[J]. IEEE Transactions on Industrial Electronics, 2006, 53(3): 963-973. |
| [4] | REPPA V, TZES A. Fault detection and diagnosis based on parameter set estimation[J]. IET Control Theory and Applications, 2011, 5(1): 69-83. |
| [5] | DARWISH H A, TAALAB A M I, KAWADY T A. Development and implementation of an ANN-based fault diagnosis scheme for generator winding protection[J]. IEEE Transactions on Power Delivery, 2001, 16(2): 208-214. |
| [6] | MOREIRA M P, SANTOS L T B, VELLASCO M M B R. Power transformers diagnosis using neural networks[C]//International Joint Conference on Neural Networks. Orlando, USA, 2007: 1929-1934. |
| [7] | FERRACUTI F, GIANTOMASSI A, LONGHI S, et al. Multi-scale PCA based fault diagnosis on a paper mill plant[C]//2011 IEEE Conference on Emerging Technologies & Factory Automation. Toulouse, France, 2011: 1-8. |
| [8] | ZHAO X X, YUN Y X. A fault diagnosis method combined fuzzy logic with CMAC neural network for power transformers[C]//Chinese Conference on Pattern Recognition. Nanjing, China, 2009: 1-5. |
| [9] | LAU C K, GHOSH K, HUSSAIN M A, et al. Fault diagnosis of Tennessee Eastman process with multi-scale PCA and ANFIS[J]. Chemometrics and Intelligent Laboratory Systems, 2013, 120: 1-14. |
| [10] | KARIMI I, SALAHSHOOR K. A new fault detection and diagnosis approach for a distillation column based on a combined PCA and ANFIS scheme[C]//2012 24th Chinese Control and Decision Conference. Taiyuan, China, 2012: 3408-3413. |
| [11] | CHEN X Y, YAN X F. Using improved self-organizing map for fault diagnosis in chemical industry process[J]. Chemical Engineering Research and Design, 2012, 90(12): 2262-2277. |
| [12] | DONG C L, WANG Y J, ZHANG Q, et al. The methodology of dynamic uncertain causality graph for intelligent diagnosis of vertigo[J]. Computer Methods and Programs in Biomedicine, 2014, 113(1): 162-174. |
| [13] | ZHANG Qin, DONG Chunling, CUI Yan, et al. Dynamic uncertain causality graph for knowledge representation and probabilistic reasoning: statistics base, matrix, and application[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(4): 645-663. |
| [14] | 杨佳婧, 张勤, 朱群雄. 动态不确定因果图在化工过程故障诊断中的应用[J]. 智能系统学报, 2014, 9(2): 154-160. CAAI Transactions on Intelligent Systems, 2014, 9(2): 154-160. |
| [15] | ZHANG Qin. Dynamic uncertain causality graph for knowledge representation and reasoning: discrete DAG cases[J]. Journal of Computer Science and Technology, 2012, 27(1): 1-23. |
| [16] | VERRON S, TIPLICA T, KOBI A. Monitoring of complex processes with Bayesian networks[M]//REBAI A. Bayesian Network. Rijeka, Croatia: Sciyo, 2010: 213-228. |



