2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
对于爬壁机器人而言,采用不同的移动机构会具备不同的运动特性[1, 2, 3]。近几年出现了轮腿或轮足复合式移动机构,通过将轮式和腿足式移动机构合二为一,使机器人同时具备移动速度快和越障能力强的优点[4, 5, 6],这成为爬壁机器人移动机构设计的一种新趋势。复合式机构并不是移动机构的简单叠加,而是将2种或多种不同移动机构有效结合起来,机器人能够根据环境和任务需求调整运动模式,实现复杂功能。这种设计在提高爬壁机器人运动性能的同时也增加了控制难度。因此,具有复合式移动机构的爬壁机器人的运动学建模尤为重要。只有通过运动学分析建立各输入自由度和机器人位姿之间的合理映射模型,才能为机器人的运动规划和精确控制提供依据,为实现机器人自主控制奠定基础[7, 8, 9]。
目前关于爬壁机器人复合式移动机构的运动学分析研究较少。中科院沈阳自动化所研制的一种轮足复合式爬壁机器人,直接按双足移动机构利用D-H参数法进行运动学建模[10]。哈尔滨工业大学研制的一种轮腿复合式爬壁机器人,将足式和轮式移动机构割裂开来,分别建立运动学模型并进行控制[11]。无论是简化为单一移动机构来建模还是将复合移动机构割裂开来进行建模,都降低了模型的准确性和有效性,增加了机器人控制的难度,并不适用于具有复合式移动机构的爬壁机器人。
本文针对爬壁机器人的一种新型轮足复合式移动机构[12],探索正逆运动学建模方法。通过位姿变换矩阵将2种基本运动学模型结合起来构建复合运动模式的运动学表达式。同时为适应机器人的壁面过渡功能,将附着面姿态参数引入到运动学表达式中,解决了具有交叉面过渡功能的复合式移动机构运动学求解问题。针对逆运动学求解中的多解问题,提出一种基于吸附安全性考虑的求解方法。上述方法为所提出的复合式移动机构的运动学求解提供了一种可行的解决方案。
1 爬壁机器人机构及运动模式分析文中爬壁机器人的设计理念是利用一种特殊设计的行星轮系结构将双足移动机构和三轮移动机构有效结合起来,构建一种轮足复合式移动机构。此方案使机器人结合2种移动机构各自的优点,提高爬壁机器人的整体运动性能。如图 1所示,该机器人主要由三部分组成:真空模块、负压模块和行星轮系。由机构简图可知,机器人共有4个自由度。直线驱动关节有1个自由度,实现真空吸盘的伸缩运动。行星轮系机构有1个自由度,实现2个模块之间的翻转。轮式移动机构有2个自由度,2个驱动轮各自单独驱动实现轮式移动功能。
根据移动机构中不同驱动关节之间的配合情况,该爬壁机器人可以实现双足运动模式、轮式运动模式和复合运动模式,并且运动模式之间可以自由灵活切换。1)双足运动模式指仅依靠行星轮系的翻转运动和真空吸盘的伸缩来实现的运动形式。双足运动模式主要用来跨越或规避障碍。另外,在平面上也可依靠双足运动模式实现直线运动。2)轮式运动模式,即双驱动轮运动模式,指2个驱动轮各自单独驱动,通过控制驱动轮转速实现移动功能的运动形式。轮式运动模式主要用来在平整壁面实现快速移动及转向等功能。3)复合运动模式,指爬壁机器人同时执行上述2种运动模式,实现机器人位置和自身姿态的同时调整。该运动模式主要在跨越交叉壁面时发挥作用。

|
| 图 1 爬壁机器人样机及其机构简图 Fig. 1 Prototype and schematic diagram of mechanism of the wall-climbing robot |
针对爬壁机器人3种运动模式的特点,依据不同方法分别构建运动学模型,在应用中根据具体情况利用不同模型对机器人进行运动控制和规划。
首先利用坐标系对机器人的环境状态进行描述。如图 2所示,坐标系构建原则如下:坐标系{0}为机器人固连坐标系,坐标原点为两驱动轮与地面接触点的中点,轴Y0与驱动轮轮轴平行,轴X0指向前轮方向;坐标系{s}为附着面坐标系,轴Zs为附着面法线方向;坐标系{g}为世界坐标系,轴Zg与重力方向相反;轴Xs、Xg都与壁面交线AB垂直。通过参数β和θ即可定义外部状态,β为附着面与水平面的夹角,θ为轴X0和轴Xs的夹角。
从附着面坐标系到世界坐标系的变换关系为

|
| 图 2 机器人基本状态参数 Fig. 2 Parametric representation of the robot's basic state |
双足运动模式下,爬壁机器人的2个模块交替附着壁面。其状态分2种情况:负压模块吸附壁面、真空模块运动;真空模块吸附壁面、负压模块运动。以第1种情况为例,利用D-H参数法进行运动学分析[13]。真空模块吸附壁面时的情况类似。
对机器人各关节配置坐标系,如图 3所示。坐标系{0}是机器人的固连坐标系。坐标系{1}到坐标系{4}分别配置于负压模块、连杆、真空模块和真空吸盘。其中坐标系{4}的原点在吸盘中心。li{i=0,1,2,3}代表相应连杆长度,θ2,θ3,d4是关节变量。行星轮系结构的2个齿轮外壳设计齿数和半径都相同,根据传动原理可知θ2和θ3的变化量始终相等,且θ3=θ2+π。
双足运动模式下的运动学表达式为

|
| 图 3 双足运动模式下的坐标系配置 Fig. 3 Coordinate systems under the BLM |
轮式运动模式下,负压模块吸附壁面,依靠密封腔内部的3轮移动装置实现机器人运动。此时机器人具有沿轴Xs和Ys的平动自由度以及绕轴Zs的转动自由度。轮式运动模式下可以限定机器人具有直线运动和转向运动2种运动形式。机器人的基本运动状态如图 4所示,机器人负压模块在轮式运动模式下由初始状态(x,y,θ)运动到(x′,y′,θ′)。机器人位姿用变换矩阵表示为

|
| 图 4 轮式运动模式下的坐标系配置 Fig. 4 Coordinate systems under the WLM |
若是直线运动,即两驱动轮转速相同,则

若是转向运动,机器人本体位姿的变化为

机器人在坐标系{s}中的实时位姿表示为
另外,平面内轮式运动模式下机器人的速度可表示为线速度和角速度。将速度表达式在附着面坐标系中表达,可得
则轮式运动模式下的运动学方程为

当执行复合运动模式时,轮式运动模式和双足运动模式共同发挥作用使机器人末端吸盘达到规定位姿。复合运动模式的运动学方程可通过式(9)变换矩阵获得。

式(9)既考虑了机器人本身的位姿,还通过gsT引入了附着面的姿态参数,有利于机器人在不同壁面连续运动时利用该模型进行运动规划和控制。
3 逆向运动学分析机器人在应用中根据实际任务需求,合理利用不同运动模式来满足位姿的要求。因此,在逆运动学求解中,首先判断机器人需要启动的运动模式,再求解相关关节运动参数。机器人最终位姿由x、y、θ、θ2、θ3及d4决定,它们作为系统状态量。
在附着面坐标系下,末端位姿表示为

运动模式的判断流程如下:
1)若s4T在双足运动模式的工作空间内,则只需启动双足运动模式,需要计算θ2、θ3和d4。
2)若(ax,ay,az)=(0,0,1),则只需启动轮式运动模式,需要求解x、y和θ或Δx、Δy和Δθ。
3)若以上2项都不符合,则启动复合运动模式,需要计算全部系统状态量。
3.1 双足运动模式的逆运动学分析在双足运动模式下,已知s4T和s0T,求解θ2、θ3和d4,则
首先确定θ2的范围,如表 1所示。
| 正负号关系 | θ2取值范围 |
| a′x>0,a′z>0 | (0,π/4) |
| a′x>0,a′z<0 | (π/4,π/2) |
| a′x<0,a′z<0 | (π/2,-3π/4) |
| a′x<0,a′z>0 | (3π/4, π) |
根据正向运动学方程推导得
另外

在轮式运动模式下,已知s4T和04T(各关节变量已知),求解x、y、θ。则
可求得

然后初步判断θ的取值范围,如表 2所示。
| 正负号关系 | θ取值范围 |
| cos θ>0,sin θ>0 | (0,π/2) |
| cos θ<0,sin θ<0 | (-π,-π/2) |
| cos θ>0,sin θ<0 | (-π/2,0) |
| cos θ<0,sin θ>0 | (π/2,π) |
由此可推得

在实际操作过程中,通过控制两驱动轮转速使机器人先沿轴Zs转过角度γ(如图 4所示),然后移动负压模块使坐标系{0}的原点到达坐标点(x,y),最后沿轴Zs转过角度θ-γ即可达到指定位姿。
3.3 复合运动模式的逆运动学分析本节从复合运动模式的实际功能出发,以交叉面跨越为例阐述复合运动模式逆运动学求解方法。已知各墙壁面坐标系之间的变换矩阵,求解机器人各驱动关节的运动参量:Δx、Δy、Δθ、θ2、θ3及d4。
如图 5所示,已知过渡面坐标系{s′}在附着面坐标系{s}中的变换矩阵表达式为
过渡面坐标系可以通过以下变化获得:先将坐标系{s′}与坐标系{s}重合,将{s′}绕轴Zs′旋转Δθ角,再绕轴Ys′旋转α角。则


|
| 图 5 跨越交叉面示意 Fig. 5 Diagram of wall transition |
Δθ的取值范围为(-π,π),根据表 3可获得Δθ的具体取值范围。
| 正负号关系 | Δθ取值范围 |
| sx′>0,sy′>0 | (-π/2,0) |
| sx′<0,sy′<0 | (π/2,π) |
| sx′>0,sy′<0 | (-π,-π/2) |
| sx′<0,sy′>0 | (0,π/2) |
据此可推得
α代表过渡面间的夹角,其取值范围为(0,π),根据表 4可判断α的具体取值范围。
| 正负号关系 | α取值范围 |
| nz′与az′同号 | (π/2,π) |
| nz′与az′异号 | (0,π/2) |
则过渡面间的夹角α为
根据机器人壁面过渡状态时的几何关系和行星轮系的运动机理可知,θ2的值仅和α有关,其关系表达式为
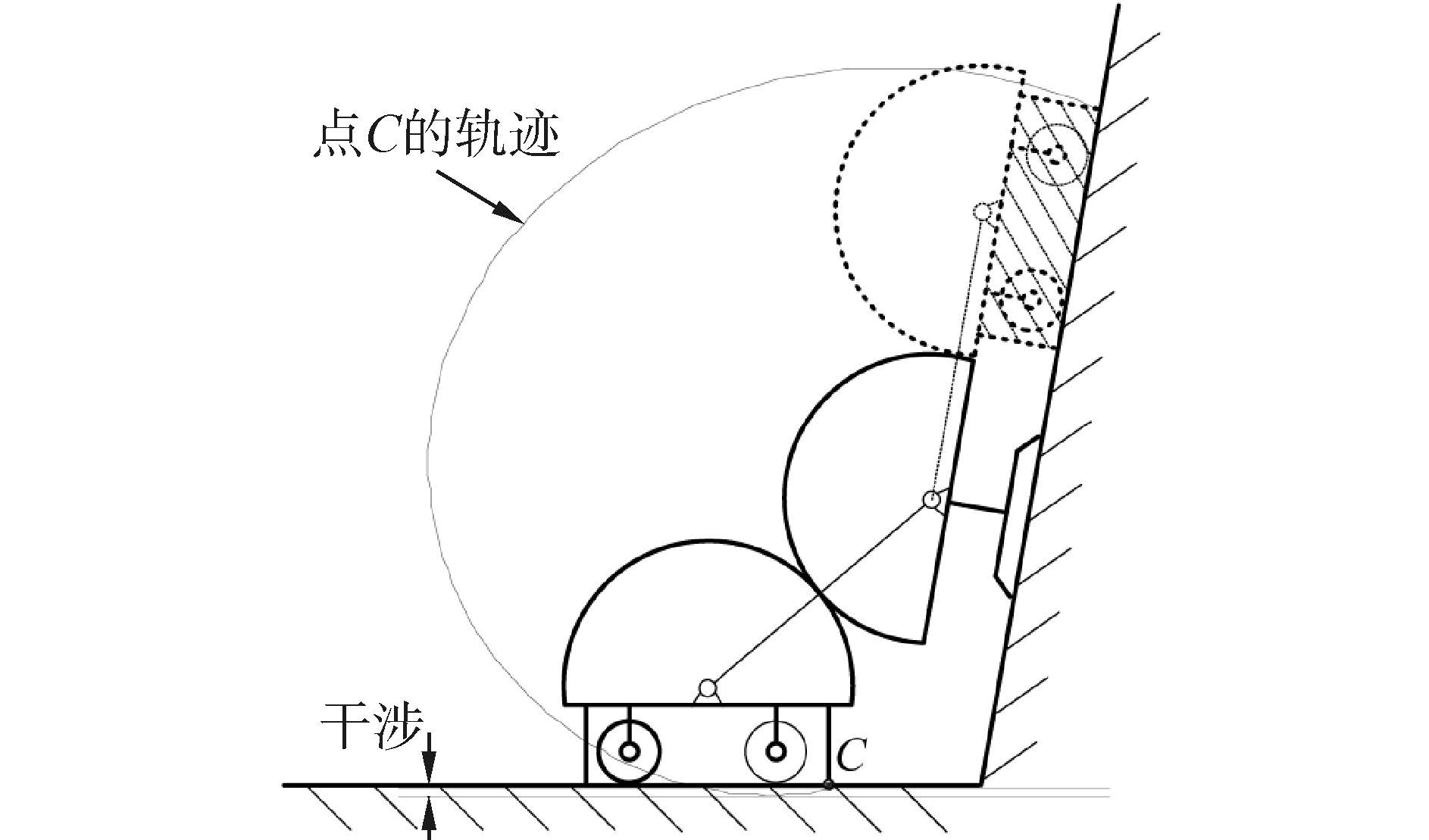
根据爬壁机器人的设计,d4的取值范围为(-l1-d,-l1+d)。当d4取该范围内的任意值时理论上都能实现壁面过渡,但该值会对壁面过渡过程的吸附安全性产生影响。吸附安全性主要考虑2个因素:过渡过程中机器人与壁面的干涉量以及所需吸附力的大小。此外,在壁面过渡过程中,有2种运动控制策略:一种是先让吸盘附着过渡面,再改变吸盘伸缩量,然后进行交叉面跨越(先吸后变);另一种策略是先改变吸盘伸缩量至合适值,再吸附过渡面,然后进行交叉面跨越(先变后吸)。本文从吸附安全性角度考虑,确定参数取值和控制策略的最优方案。如图 6所示,点C为密封圈与壁面接触点,壁面过渡过程中点C的轨迹表明机器人负压模块和附着面存在干涉,尽管从机器人设计角度(弹性密封圈设计)是可以容忍干涉的存在,逆运动学求解时要使此过程中的最大干涉量尽可能小。同时要使过渡过程中真空模块所需提供的吸附力尽可能小,提高机器人运动过程中的安全性。
|
| 图 6 壁面过渡干涉示意 Fig. 6 Diagram of interference during wall-transition |
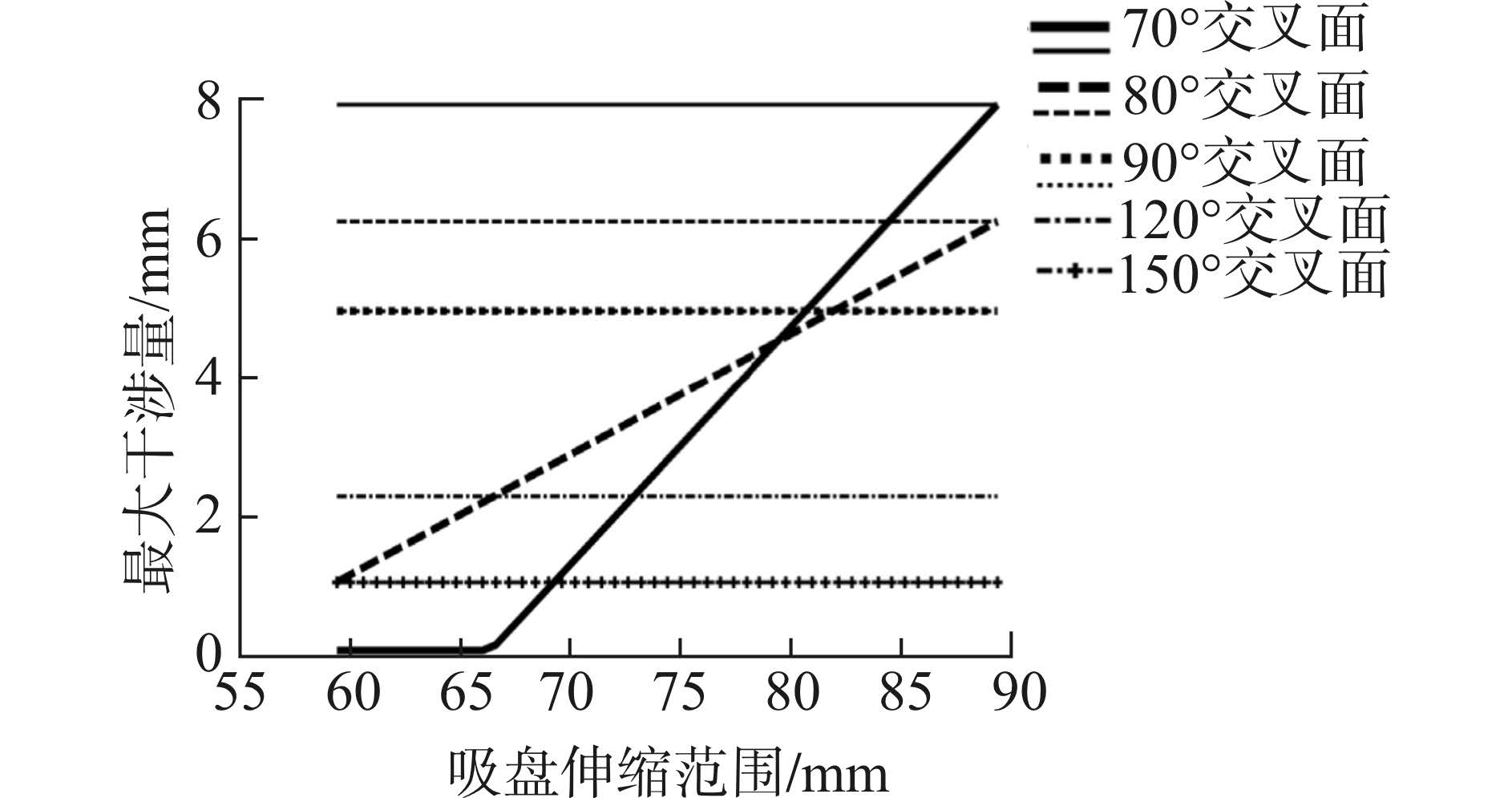
图 7所示为跨越不同角度交叉面时的最大干涉量变化情况,图中细线代表“先变后吸”策略,粗线代表“先吸后变”策略,可知:跨越锐角交叉面时,先吸后变的策略比先变后吸的策略干涉量更小;跨越直角交叉面时,2种策略下的最大干涉量相同;跨越钝角交叉面时,只能采用先变后吸的策略。此外,采用先吸后变的策略时,吸盘越短,壁面过渡过程中的最大干涉量越小;采用先变后吸的策略跨越交叉面时,吸盘伸缩量对壁面过渡过程中的最大干涉量无影响。
综上所述,从交叉面过渡过程中干涉量大小的角度考虑,跨越锐角交叉面时,采用先吸后变的策略,且吸盘应尽量短;跨越钝角交叉面时,采用先变后吸的策略,吸盘伸缩量对最大干涉量无影响。
|
| 图 7 不同控制策略下壁面过渡时的最大干涉量 Fig. 7 The maximum interference under different control strategies |
图 8所示为跨越不同角度交叉面时重心与壁面间的距离变化情况,可知:当吸盘伸缩量和交叉面夹角一定,2种控制策略下重心与过渡面之间的最大距离相同;无论采用哪种控制策略进行交叉面过渡,只要吸盘伸缩量确定,无论交叉面夹角如何变化,运动过程中重心与过渡面最大距离不变;跨越同一交叉面时,吸盘越短,重心与过渡面最大距离越小,意味着运动过程中所需吸附力越小。

|
| 图 8 不同控制策略下壁面过渡时重心与过渡面最大距离 Fig. 8 The maximum distance between the wall and the center of gravity under different control strategies |
综上所述,从交叉面过渡过程中所需提供吸附力大小的角度考虑,无论采用哪种控制策略,吸盘越短越安全。
因此在进行交叉面过渡的逆运动学求解过程中,在确定α的值后,根据其属于锐角、直角还是钝角,确定不同的控制策略以及吸盘伸缩量的值。 根据以上逆运动学分析,可以获得复合运动模式下交叉面过渡的运动控制流程,如图 9所示。

|
| 图 9 交叉面过渡过程控制流程 Fig. 9 The control flow chart of wall transition |
针对所构建的正逆运动学模型和求解方法,以跨越交叉壁面为例进行仿真试验验证。实验环境如图 10所示,利用2块铝板搭建120°交叉壁面环境,爬壁机器人综合利用各种运动模式实现交叉面过渡。其中样机基本参数如表 5所示。

|
| 图 10 跨越交叉壁面实验 Fig. 10 Experiment of wall transition |
| 参 数 | 数 值 |
| 驱动轮直径 dw | 40 |
| 行星轮系系杆长度l2 | 146 |
| 直线关节的连杆参数l3 | 10 |
| 直线关节的关节变量d4 | (35,85) |
| 前后轮轴线间距B | 85 |
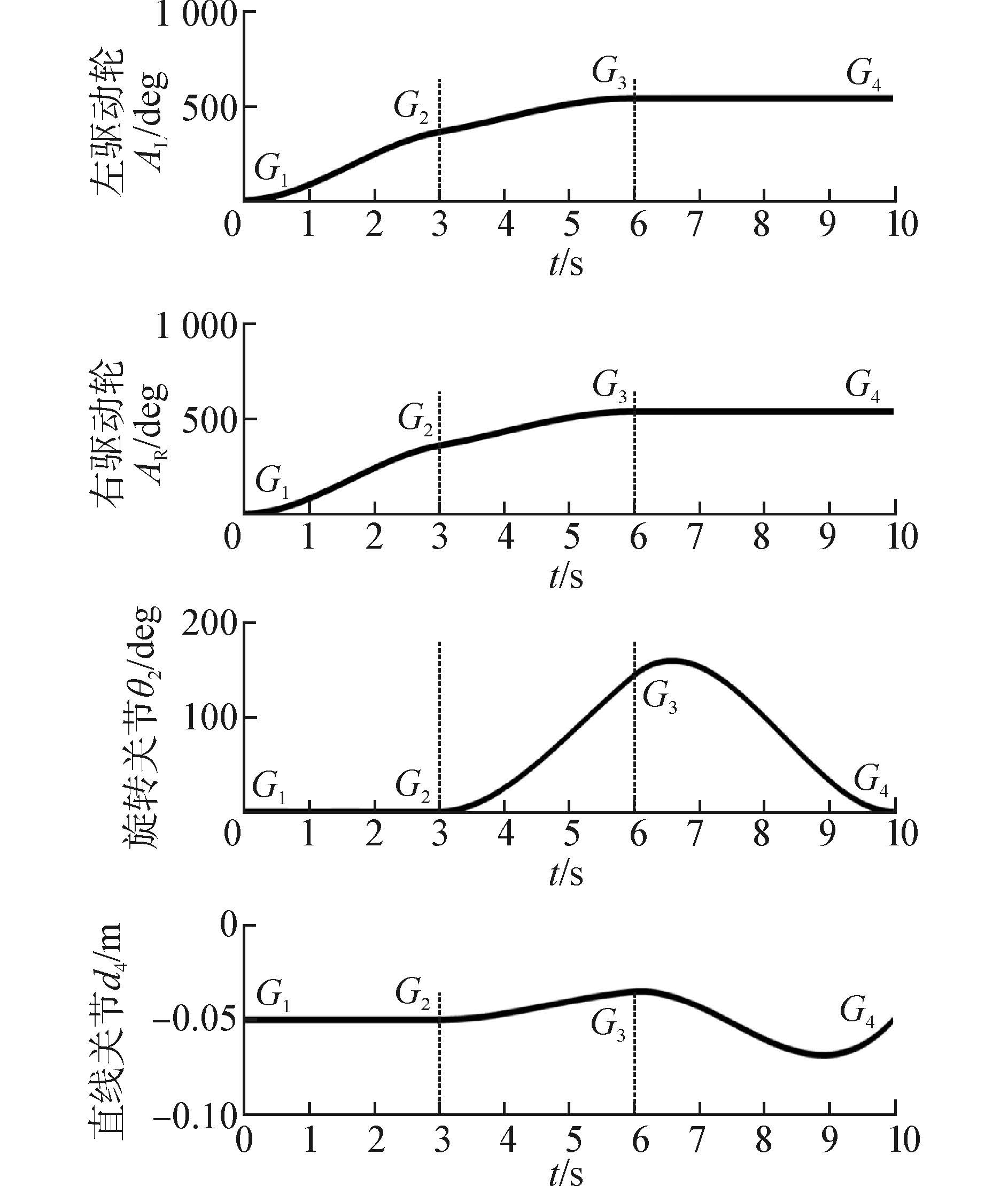
如图 11所示,对于跨越120°交叉壁面,共分成3个阶段完成。阶段I为轮式运动模式下机器人从初始位姿G1到达位姿G2。阶段II为复合运动模式下机器人从位姿G2到达位姿G3。阶段III为双足运动模式下机器人从位姿G3到达位姿G4。通过3个阶段的运动实现交叉壁面的跨越。位姿Gi(i=1,2,3,4)的表达式如式(22)所示。

|
| 图 11 正向运动学分析 Fig. 11 Analysis of forward kinematics |
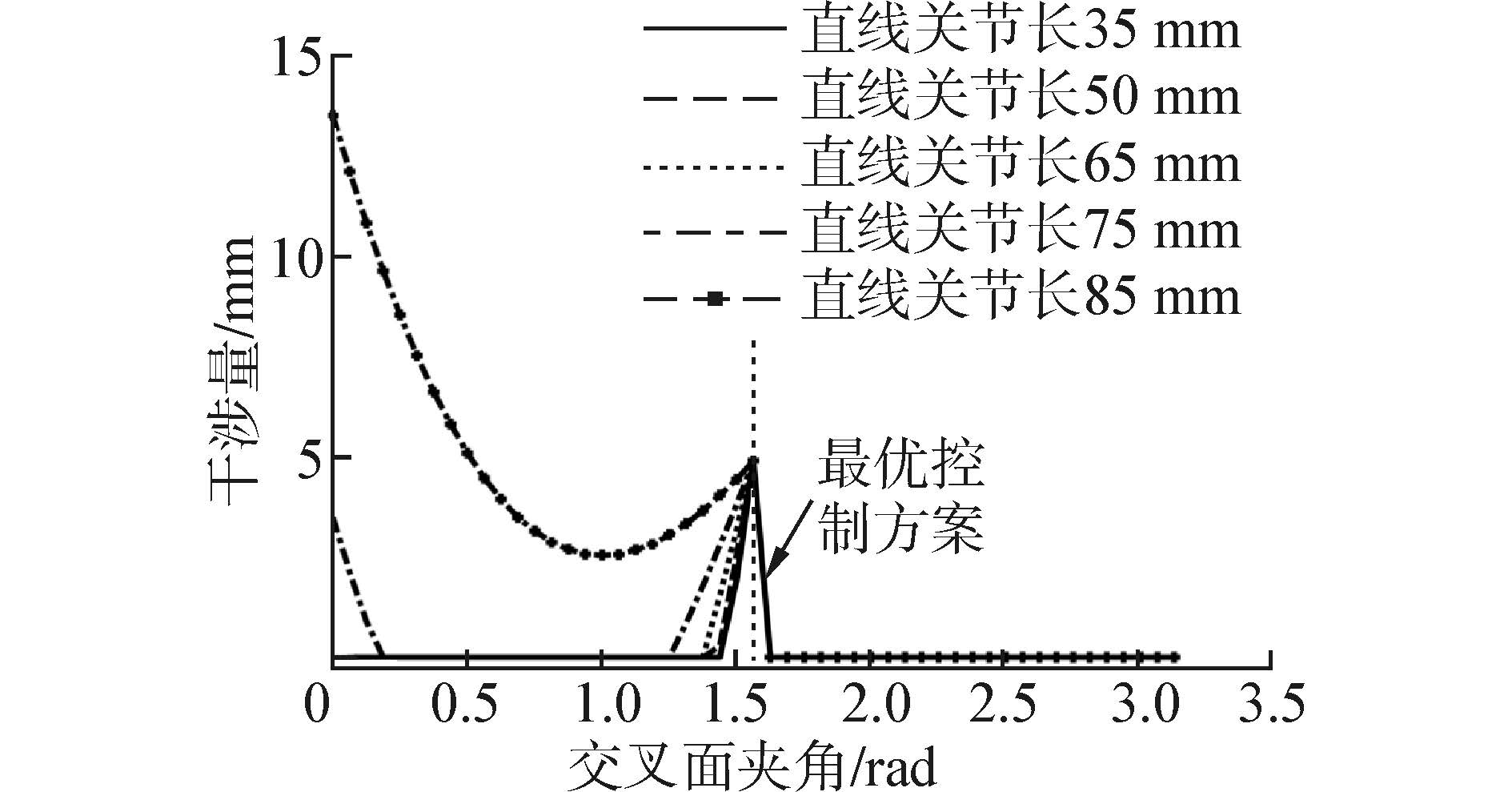
基于所提出的正向运动学模型,以图 11所示的关节变量为输入可得到在附着面坐标系{s}中的吸盘末端轨迹,如图 12所示。由图可知吸盘末端运行轨迹的仿真结果与样机实际操作一致,真空吸盘能够接触过渡面,保证下一步运动的实施。以关键点位姿Gi(i=1,2,3,4)作为逆运动学仿真输入可以得到关节变量值位于关节规划轨迹上,从而相互验证了运动学正逆解的正确性。图 13所示为针对5种不同直线关节变量的值,跨越0°~180°交叉面时最大干涉量的变化。采用所述优化方案将壁面夹角大小(锐角、钝角)与控制策略(先变后吸、先吸后变)相结合,可获得逆解最优方案,解决了直线关节变量的多解问题。

|
| 图 12 吸盘末端轨迹 Fig. 12 Trajectory of suction cup |
|
| 图 13 不同直线关节伸缩量下干涉量大小 Fig. 13 The interference under different lengths of translation joint |
本文针对具有轮足复合式移动机构的爬壁机器人的运动学建模展开研究。对复合式移动机构的3种运动模式分别建立了运动学模型,利于机器人在不同壁面连续运动时利用运动学模型进行运动规划和控制。针对逆运动学分析,利用位姿变换矩阵建立了运动模式的判断流程。以此为基础并基于吸附安全性考虑构建复合运动模式下的逆运动学求解优化方案。最后通过交叉壁面跨越对所提方法进行仿真实验验证,该方法对所研制的复合式移动机构具有很好的适应性。在未来工作中,将结合传感器进一步提高爬壁机器人壁面运动的自主性。
| [1] | NISHI A. Development of wall-climbing robots[J]. Computers & Electrical Engineering, 1996, 22(2): 123-149. |
| [2] | CHU B, JUNG K, HAN C S, et al. A survey of climbing robots: locomotion and adhesion[J]. International Journal of Precision Engineering and Manufacturing, 2010, 11(4): 633-647. |
| [3] | TUMMALA R L, MUKHERJEE R, XI N, et al. Climbing the walls[J]. IEEE Robotics & Automation Magazine, 2002, 9(4): 10-19. |
| [4] | LONGO D, MUSCATO G. The Alicia3 climbing robot: a three-module robot for automatic wall inspection[J]. IEEE Robotics & Automation Magazine, 2006, 13(1): 42-50. |
| [5] | XIAO J Z, SADEGH A, ELLIOT M, et al. Design of mobile robots with wall climbing capability[C]//Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Monterey, USA, 2005: 438-443. |
| [6] | FU Y L, LI Z H, YANG H J, et al. Development of a wall climbing robot with wheel-leg hybrid locomotion mechanism[C]//IEEE International Conference on Robotics and Biomimetics. Sanya, China, 2007: 1876-1881. |
| [7] | 王斌锐, 冯伟博, 骆浩华, 等. 曲面上双足三自由度爬壁机器人设计与稳定性分析[J]. 机器人, 2014, 36(3): 349-354. WANG Binrui, FENG Weibo, LUO Haohua, et al. Design and stability analysis of dual-foot 3 DOF climbing robot for blade surface[J]. Robot, 2014, 36(3): 349-354. |
| [8] | BAYLE B, RENAUD M, FOURQUET J Y. Nonholonomic mobile manipulators: kinematics, velocities and redundancies[J]. Journal of Intelligent and Robotic Systems, 2003, 36(1): 45-63. |
| [9] | 王洪光, 姜勇, 房立金, 等. 双足爬壁机器人壁面凹过渡步态规划研究[J]. 智能系统学报, 2007, 2(4): 40-45. WANG Hongguang, JIANG Yong, FANG Lijin, et al. Gait planning of concave transitions between different slopes for bipedal wall-climbing robots[J]. CAAI Transactions on Intelligent Systems, 2007, 2(4): 40-45. |
| [10] | 刘爱华, 王洪光, 房立金, 等. 一种轮足复合式爬壁机器人机构建模与分析[J]. 机器人, 2008, 30(6): 486-490. LIU Aihua, WANG Hongguang, FANG Lijin, et al. Modeling and analysis of a biped-wheel wall-climbing robot mechanism[J]. Robot, 2008, 30(6): 486-490. |
| [11] | 李志海. 轮足混合驱动爬壁机器人及其关键技术的研究[D]. 哈尔滨: 哈尔滨工业大学, 2010: 30-36. LI Zhihai. Study on wheel leg hubrid wall climbing robot and its key technology[D]. Harbin, China: Harbin Institute of Technology, 2010: 30-36. |
| [12] | DONG W G, WANG H G, LI Z H, et al. Development of a wall-climbing robot with biped-wheel hybrid locomotion mechanism[C]//2013 IEEE/ASME International Conference on Intelligent Robots and Systems. Tokyo, Japan, 2013: 2333-2338. |
| [13] | CRAIG J J. Introduction to robotics: mechanics and control[M]. Upper Saddle River, USA: Pearson Education, 2005: 62-69. |



