动态任务调度可以根据运行的时情况动态地将任务分配到各个内核上,由于需要实时地收集、存储并分析状态信息,动态调度的实施有一定的系统开销,但这种开销和付出通常是有回报的[1]。多核处理器系统中的任务调度已被证明是NP问题[2],除个别特殊情况外,目前尚未有一种多项式时间算法可以求得最优解,只能得到一个最大限度接近最优解的解,因此改进算法的效率并构建任务调度实现机制成为研究重点,很多学者在这方面做了大量工作。
比较经典的调度算法有Min-Min[3]、Max-Min[4]、MCT[5]、MET[6]算法。Min-Min算法实现简单、执行速度快。算法首先通过计算待调度任务在任一可用内核上的最早完成时间,取最小值作为该任务的最早完成时间,然后选取所有待调度任务中最早完成时间最小的一个任务进行调度。缺点是如果任务集中存在过多的执行时间比较小的任务,那么大任务将无法得到及时的执行。Max-Min算法同Min-Min算法类似,同样需要计算每一任务的最早完成时间,不同的是Max-Min算法首先调度最早完成时间最大的任务,将其分配到对应的内核上。缺点是小任务等待时间过长、影响执行效率,也可能造成负载不均衡。MCT算法以任务完成时间最早为目标进行调度,每次将到达的任务分配到完成时间最早的内核上,但该算法忽略了任务的执行时间,可能将任务分配到执行时间较长的处理机上运行。MET算法以任务执行时间最短为目标进行调度,每次将到达的任务分配到执行时间最短的内核上,其缺点是易造成较强内核负载过多任务,导致内核间负载不均衡,降低系统性能。
清华大学的石威等[7]提出了一种相关任务图的均衡动态关键路径调度算法,采用动态关键路径技术并均衡考虑关键路径结点和非关键路径结点,优先调度对相关任务图调度长度影响最大的就绪结点,从而极大地缩短任务图的调度长度。李仁发[8]对多核处理器系统任务调度研究进展进行讨论,对不同模型下的多核系统任务调度算法相关研究进行了分析总结,从调度算法分析和调度实现框架2个方面探讨了近年来多核任务调度的国内外研究进展情况。文中对任务分配、任务模型优化、调度器实现和任务迁移等当前亟待解决的问题,进行了深入探讨,并指出了下一步主要的研究方向,为多核处理器相关研究提供参考。吉林大学的耿晓中提出了一种动态负载均衡模型[9],将影响多核处理器负载均衡的因素分为5类:多核系统的负载均衡环境、用户提交的任务属性、系统的负载评价、系统所采用的调度策略以及系统的调度评价指标,为多核动态调度的负载平衡研究提供了理论指导;徐雨明等[10]将遗传算法和启发式方法有机地结合,根据染色体双螺旋结构模型,提出了一种异构系统中依赖任务调度的双螺旋结构遗传算法。该算法首先采用启发式方法,产生较佳的任务调度优先队列,然后模仿碱基互补配对方法,提高算法的有效性和收敛速度;Vinay等[11]提出一种多核处理器动态任务调度策略,调度思想是依据任务的执行时间和依赖此任务的任务数量确定此任务优先级,当某个内核空闲时,选择一个优先级最高且为就绪状态的任务分配给该内核。此策略结构简洁,算法复杂度低,但每个内核上只分配一个任务,且调度时需要对数据段加锁以保证数据一致性,当内核数目较多时,经常发生多个内核同时申请分配任务的情况,所以不可避免出现内核空闲等待现象,不能完全发挥多核处理器优势。
文中对文献[11]的动态调度策略进行改进,克服内核可能空闲等待问题,并综合负载均衡策略,提出多核动态任务调度算法(shared task data structure,STDS)。算法通过分析任务等待时间、任务间通信开销和内核负载等因素,确定任务优先级,并据此分配任务。通过仿真实验验证,该算法在保证任务处理速度的同时有较好负载均衡,比较适用于内核数目较多的系统。
1 模型在多核任务调度研究中,为便于研究理解,通常用抽象的任务调度模型描述任务调度系统。多核任务调度模型通常由系统模型、任务模型、任务调度算法和任务映射图组成。
1.1 系统模型系统模型是指依据系统硬件环境构建出可进行数学量化分析的数学模型,文中用二元组SM(system model)={P,Rate}表示,其中:SM表示系统模型;P={P0,P1,…,Pk,…,Pm-1}为处理器内核集合,Pk表示第k个处理器内核,|P|=m为处理器中内核的总个数。多核处理器根据内核在执行能力方面的差别可划分为同构和异构2类,同构多核处理器通过增加同种处理器内核数量提升性能,而异构多核处理器通过集成不同计算能力的内核来优化处理器,实现多核处理器性能发挥的最大化,在能耗、面积等方面有着巨大的优势[12]。文中以有限数目的异构多核处理器为研究基础,集合P中处理器内核速度并不完全相同,用spk表示内核Pk的处理速度。
Rate={…,Rates,t,…}表示处理器内核间数据传输速率集合,元素Rates,t表示处理器内核Ps与Pt间的数据传输速率。
核间互连技术是多核处理器设计的关键,当前多核处理器核间互连方式主要有总线共享、交叉开关互连和片上网络3种。文中对多核处理器核间互连技术不做具体研究,默认任意2个处理器内核间均存在数据通信通路,即对于任意的s(0≤s≤m-1)和t(0≤s≤m-1),Rates,t≠0。为简化环境模型,假设同一时刻,内核Pk只能与一个内核进行通信。
1.2 任务模型任务模型是描述任务属性和特征的一种数学模型,它包含任务调度过程中的状态和控制等信息。STDS算法构建了一个可以共享访问的TDS(task data structure)结构,TDS由若干数据项构成,每个数据项唯一对应一个任务,数据项记录该任务的相关信息,其定义如图 1所示。
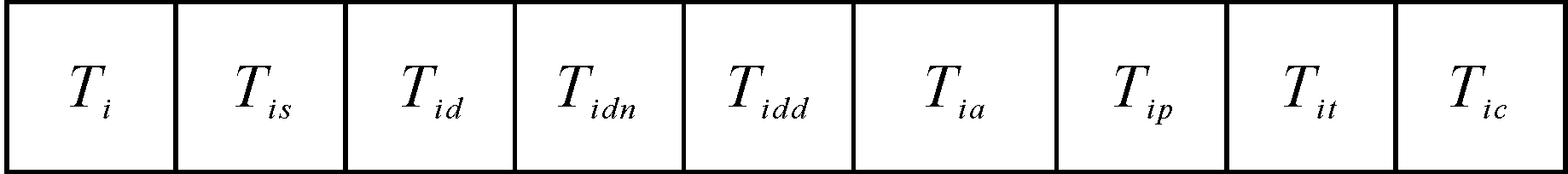 |
| 图 1 数据项定义Fig. 1 Definition of data element |
Tid={…,Tj,…}:依赖任务集合,也叫前驱任务集合,任务Ti必须在其依赖任务全部执行完成之后执行;
Tidn:依赖任务剩余数量,表示任务Ti的依赖任务集合中尚未执行完毕的任务数量,即依赖任务集合Tid中,还有多少依赖任务没有执行完成。其初值是集合Tid的长度,即Tidn=| Tid|,每当一个依赖任务执行完毕,Tidn值减1,直到Tidn=0,而Tidn=0是Tis=0(就绪)的必要条件;
Tidd={…,Datai,j,…}:与依赖任务通信数据量集合,记录任务Ti与其依赖任务Tid通信的数据大小,Datai,j表示任务Ti与依赖任务Tj通信的数据大小,如果任务Ti、Tj分别分配到内核Ps、Pt上,则任务Ti与Tj的通信时间就可用Datai,j/Rates,t表示;
Tia={…,Tj,…}:依赖任务Ti的任务集合,也叫后继任务集合,只有Ti执行完成后,其后继任务才有机会变为就绪状态,从而调度执行。当Ti完成后,需要将集合Tia中所有任务的Tidn属性值减一;
Tip:任务优先级,表示任务优先调度程度,任务优先级越高,被优先调度的可能性越大。任务优先级取决于任务就绪时间、通信开销以及内核负载等因素。系统运行过程中,就绪时间和内核负载等是动态变化的,所以任务优先级不是某一定值,它随着系统状态的改变而动态变化;
Tit:任务就绪时间,即任务满足调度条件变为就绪状态的时间。如果用 t表示现在时间,则等待时间就是(t- Tit),为避免存在长时间未能调度执行的就绪任务,算法应优先调度等待时间长的任务;
Tic:任务映射,表示任务和内核的对应关系,即任务Ti分配到哪个内核上执行。STDS算法用-1表示任务尚未分配内核资源,用整数0,1,…,m-1分别表示在内核P0,P1,…,Pm-1上执行。
1.3 调度器模型文中设计的调度器模型采用集中式调度模式,如图 2所示。图中指定了一个内核专门执行调度程序,称为中心调度器,中心调度器负责收集调度信息和执行任务调度,其余内核只负责执行任务。
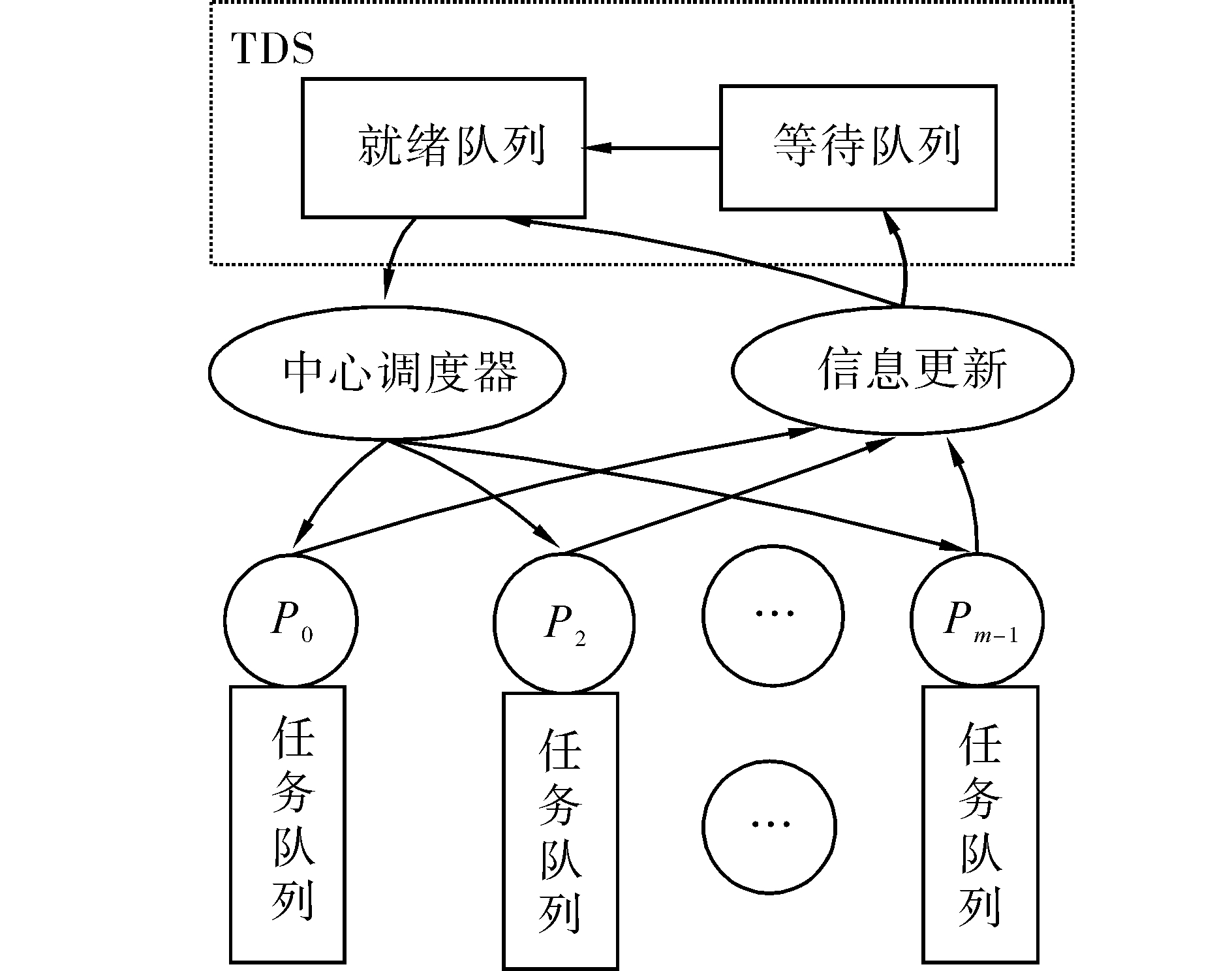 |
| 图 2 调度器模型Fig. 2 Scheduler model |
建立维护等待队列和就绪队列2个全局任务列表,调度器在任务调度时只需要检索就绪任务队列,节省了调度时间开销,等待队列中的任务满足就绪条件时可以变为就绪态等待调度。每个内核都有一个可以缓存一定数目任务的局部队列,当内核需要调度任务时直接从缓存中获取;而当局部队列中的任务过少时开始请求调度器为局部队列分配任务,降低了调度器调度频率,而且中心调度器与各内核可以并行地运行。全局调度队列和局部调度队列结合的方式在整体上是全局队列方式,与集中式调度策略配合使用易于实现负载均衡;在底层实现上是局部队列方式,降低了系统对队列共享性要求,克服了集中式调度模式的性能瓶颈问题。
文中通过重载和轻载阀值确定调度时机,当内核处于轻载状态时请求任务调度,处于重载时不允许再向内核分配任务,这种策略在保证一定负载均衡效果的同时提高了内核执行效率。
2 任务优先级将任务分配到最合适的内核上是任务调度的核心问题,而任务优先级计算是任务分配的关键,任务优先级表明任务被优先调度程度。在多核环境下,各内核的状态不尽相同,STDS算法为评价任务与内核的适合程度,首先计算任务相对于一个确定内核的优先级Tipk,然后取其在所有内核上的最大值作为任务优先级Tip,表示为式(1):
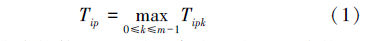
多核处理器的负载均衡要求避免出现一个或多个内核负载较低甚至空闲,而其他内核处于高负载状态的情况,从而充分发挥多核处理器优势。STDS算法使用任务队列长度|TLk|作为内核负载指标,内核的任务队列越长,说明分配的任务越多,所以其负载越大。
为实现负载均衡引入调度粒度,内核Pk的调度粒度定义为一次调度过程中为Pk分配的任务数量,这里的一次调度过程是指一个内核请求调度,调度算法为其分配任务的过程,在实际运行中,可能出现调度算法一次性处理多个内核调度请求,调度的任务数量等于为每个内核分配的任务数量之和。粒度大小要根据系统模型而定,调度粒度过大,不能充分发挥动态调度优势,而粒度过小,会引发频繁调度,增大调度程序运行时间开销,降低处理器效率。对于异构多核处理器,调度粒度与内核处理速度是正比关系。STDS算法将调度粒度定义为式(2):
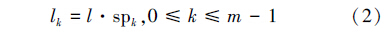
STDS算法通过限制内核任务队列长度实现负载均衡,为有效发挥调度队列作用,算法引入2个负载因子,分别确定队列的上限和下限,具体定义如式(3)~(5):
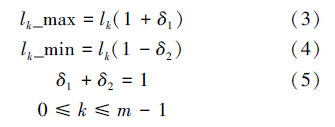
上述阐述了计算任务优先级时的内核队列上下限问题,式(6)~(10)则是对任务优先级计算时的等待时间、通信开销和内核负载均衡因素的描述。STDS算法在计算任务优先级时,综合考虑等待时间、通信开销和内核负载均衡因素,式(1)中Tipk表示任务Ti分配到内核Pk适合程度,其计算公式为:
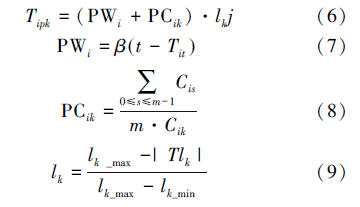
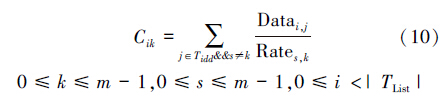
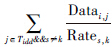 表示,下标s即任务Tj的Tjc属性值,表示任务Tj分配给内核Ps。
表示,下标s即任务Tj的Tjc属性值,表示任务Tj分配给内核Ps。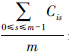 表示平均通信时间,通信时间越小,PCik值越大,优先级也相应越大,对于Cik相同的任务,若任务的
表示平均通信时间,通信时间越小,PCik值越大,优先级也相应越大,对于Cik相同的任务,若任务的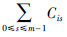 值较大,则说明此任务如果分配到内核Pk上节省的通信开销更多,相应的其优先级也较高。在实际计算时,因为任务Ti的依赖任务已经全部分配执行,所以若分配在内核Pk上,通信开销是个定值,因此PCik只需计算一次。
值较大,则说明此任务如果分配到内核Pk上节省的通信开销更多,相应的其优先级也较高。在实际计算时,因为任务Ti的依赖任务已经全部分配执行,所以若分配在内核Pk上,通信开销是个定值,因此PCik只需计算一次。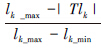 反应了内核的负载状态,|TLk|是内核Pk当前任务队列长度,当|TLk|=lk_max时其值为0,从而Tipk=0为最小值,则当前状态下不能向内核Pk分派任务。在一次调度过程中,调度程序可能需要响应多个内核的调度请求,对于|TLk|较小的内核,其Lk较大,从而实现优先将任务分配到负载较轻的内核,并进而达到负载均衡效果。
反应了内核的负载状态,|TLk|是内核Pk当前任务队列长度,当|TLk|=lk_max时其值为0,从而Tipk=0为最小值,则当前状态下不能向内核Pk分派任务。在一次调度过程中,调度程序可能需要响应多个内核的调度请求,对于|TLk|较小的内核,其Lk较大,从而实现优先将任务分配到负载较轻的内核,并进而达到负载均衡效果。
综上所述,任务优先级值的计算,是对等待时间、通信开销和内核负载3个因素综合考量的过程,其结果可能不是单一因素中最优的,但一定是综合考虑全部3种因素后最优的选择。
3 算法实现
在上节中详细介绍了任务优先级的计算,本节将介绍STDS算法的具体实现过程。
为了使任务调度算法得到较理想的实现,STDS算法的研究基于以下假设条件:
1)假设任务间的依赖关系固定不变;
2)同一内核上任务间通信开销忽略不计;
3)任务不可抢占。
系统运行时首先将任务初始化,构造TDS,由于算法中大多计算只针对就绪任务,特别是任务分配时,所以为了节约计算开销,算法初始化时会生成一个就绪任务列表和一个等待任务列表。当内核Pk任务队列长度|Tlk|≤lk_min时,就向调度程序请求分配任务,调度程序遍历就绪列表,计算相对于内核Pk的优先级,选择优先级Tip值最大的任务分配到Pk上,重复执行此过程,直到内核Pk任务队列长度|Tlk|≥lk。若同时有多个内核请求任务分配,调度程序分配任务时需要响应这几个内核的请求,计算优先级时需要计算相对于这几个内核的优先级,然后取最大值作为最终优先级,调度程序选择优先级最大的任务分配到对应的内核。
值得注意的是在动态调度过程中,为了保证数据实时有效,STDS算法在每个任务分配完成或执行结束时对数据进行更新。当任务Ti分配给内核Pk后,需要将任务Ti对应数据项中的Tic置为k,此时内核Pk负载也相应改变;当任务Ti执行完成时,如果任务Tj依赖任务Ti,需要将任务Tj的Tidn值减1,若减1后Tidn=0,将任务Tj状态置为就绪态并从等待列表移到就绪列表。为了降低复杂度节省时间,STDS算法采用先记录再批量执行的方式,即在任务执行期间暂时将完成的任务编号记录,在任务调度程序执行时批量更新数据;如果任务Ti执行完毕且所有依赖Ti的任务也执行完毕,就将任务Ti的信息从TDS中删除,从而释放内存节省空间。
如果就绪列表为空,调度程序不会响应内核的任务分配请求,当就绪列表和等待列表全为空时,说明任务全部执行完毕,调度结束。
STDS算法实现步骤:
Procedure STDS(SM,TDS,PList,TLexe)/*SM表示处理器内核系统;TDS是所有任务信息;PList是需要分配任务的内核列表,TLexe是执行完毕但还未进行信息更新的任务列表*/
1){for each Ti∈TLexe
2) { Tia[]←Ti;
3) for each Tj∈Tia
4) Tjdn←Tjdn-1; /*执行完毕的任务信息更新,将其后继任务的依赖任务数量减一*/
}/* end for each Ti∈TLexe */
5) TLready[]←TDS;/*就绪任务放入就绪队列*/
6)for each Ti∈TLready
7){ for each Pk∈PList
8) Cik←式(10); /*任务Ti若在内核Pk上与前驱任务的通信开销,只需计算一次 */
}/* end for each Ti∈TLready */
9)while(TLready≠ Ø and PList≠Ø)
10){ for eachTi∈TLready
11) { PWi←式(7);
12) for eachPk∈PList
13) { PCik←式(8);
14) Lk←式(9);
15) Tipk←式(6);
}/* end for each Pk∈PList */
16) Tip=max{Tipk};
}/* end for each Ti∈TLready */
17) Tj←max{ Tip };/*选出最大优先级的任务,设Tj就是选出的任务,且其对应内核为Ps,即Tjp= Tjps */
18) TLs←TLs+{Tj};/*任务Tj分配给内核Ps*/
19) TLready←TLready-{Tj};
20) Tjc=s;
21) if |TLs|=ls_maxthen PList←PList-{Ps};
/*内核Ps分配任务结束*/
22) if TLready≠ Ø then return; /*没有就绪任务*/
}/* end for while*/
}
其中1)~5)是算法对执行完毕但未进行数据更新的任务进行处理,将其后继任务的Tidn属性值减1,且减为0时放入就绪队列等待调度。算法中有两重循环,外层循环遍历TLexe列表,内层循环遍历后继任务列表,所以时间复杂度为 O(n)×O(logn)=O(nlog n)。而任务更新发生在每次任务分配时,次数大约为任务数量与调度粒子比值即n/l,而在具体应用环境中调度粒子为定值,所以数据更新总时间复杂度为O(n2log n)。6~20是进行任务分配,其中优先级计算是关键。计算每个任务相对于每个请求分配任务内核的优先级,其时间复杂度为O(mn),其中m是内核数量,n是就绪任务数量。而算法最终需要将任务全部分配完成,所以任务分配的总时间复杂度为O(mn)×O(n)=O(mn2)。因此STDS算法的时间复杂度为O(n2log n)+O(mn2)= Max(O(n2log n),O(mn2)),而经典Min-Min算法的时间复杂度为O(mn2)[13],两者处于同一量级。
4 实验任务调度目前还没有形成统一规范的性能测试方案[14],大多数对调度算法的研究都是采用随机DAG图生成器来生成各种不同形状的DAG图集合作为任务调度算法的测试用例。
文中借助TGFF工具生成随机任务图,并以此完成TDS初始化,用内核上任务长度表示负载情况,通过任务总执行时间和负载均衡等衡量算法优劣,在Simics[15]模拟平台上对本文算法性能进行模拟实验测试。为了测试本文提出的算法对并行任务调度问题的求解效果,采用下面2类实验来验证。
4.1 参数对调度算法的影响STDS算法用到的参数有:粒度因子l、负载因子δ1和δ2、实时性因子β。l的大小决定一次调度过程分配的任务数量,进而决定调度频度;l、δ1和δ2共同影响着负载均衡;β主要调节算法实时性。下面分别通过实验数据说明参数l、δ1、δ2、β对STDS算法性能的影响。
1)调度粒度对STDS算法调度频度和负载影响
通过TGFF工具分别生成具有3 000个任务和5 000个任务的随机任务图,测试这2类任务在不同调度粒度下的调度效果,为屏蔽其他因素影响,设置参数β=0,lk_min=lk(1-δ2)=2,结果如图 3所示。由图 3可以看出,调度次数随着调度粒度增大而减小,进而降低STDS调度算法消耗时间;粒度较小时调度次数减少幅度较大,而在较大粒度情况下效果较弱。
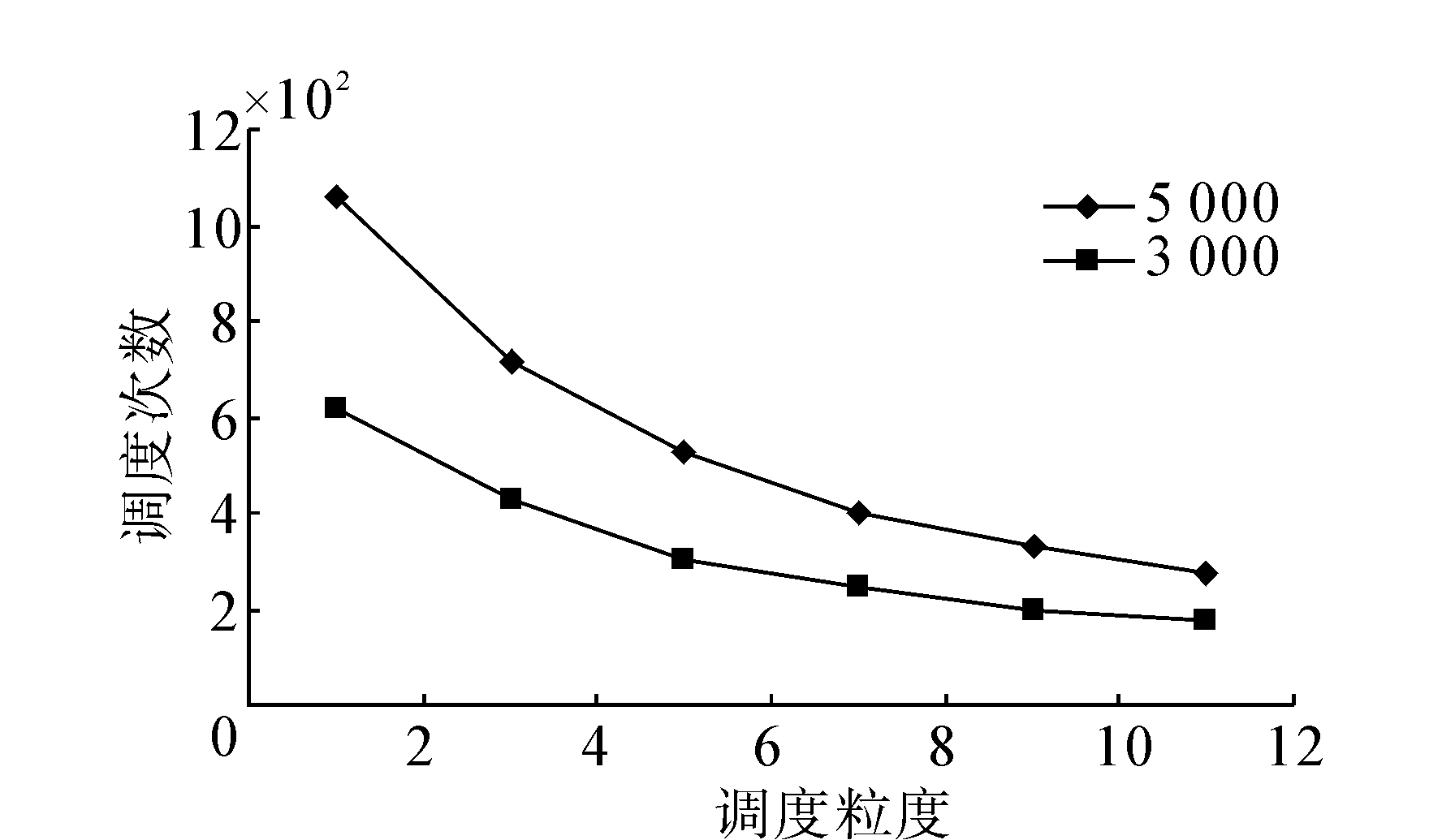 |
| 图 3 调度粒度对调度次数影响Fig. 3 Change of scheduling times in the situation of different scheduling granularities |
虽然较大粒度下节省调度时间,但并不是l取最大值时STDS算法性能最优,l取极大值时,调度频度最小,但此时对于内核Pk的请求,STDS算法会将全部就绪任务分配给Pk,从而造成各内核上负载差别较大。表 1说明了粒度对负载均衡的影响,在调度过程中对内核负载进行采样,每次采样时,用此时内核上任务队列长度占所有内核任务队列长度之和的比例,评价负载均衡效果。表 1中P0、P1、P2的处理速度为1 GHz,P3的处理速度为2 GHz,据STDS算法设定,P3的负载应为P0、P1、P2的2倍。从表 1可以看出,负载均衡效果随调度粒度的增大而降低。
| 调度粒度 | P0/% | P1/% | P2/% | P3/% |
| 2 | 19.61 | 20.44 | 20.37 | 39.58 |
| 8 | 20.11 | 19.80 | 21.19 | 38.90 |
| 14 | 22.51 | 19.13 | 20.91 | 37.45 |
2)负载因子对算法性能影响
δ1是负载上限因子,δ2是负载下限因子,δ1和δ2满足公式(5)约束条件:δ1+δ2=1,当δ2确定时,δ1的值也是确定的。δ2的大小决定了内核Pk调度队列长度下限lk_min的大小,lk_min较大时,内核Pk的负载也相对较大,然而此时会引发另一个问题,虽然内核Pk负载达到下限lk_min并请求分配任务,但此刻Pk依然有较多任务待执行,当就绪任务不是很充足时,容易发生STDS算法频繁响应分配请求。图 4是在δ2取不同值时的调度统计结果,固定调度粒度l=6,可以看出,调度次数随着δ2的增大而增大。
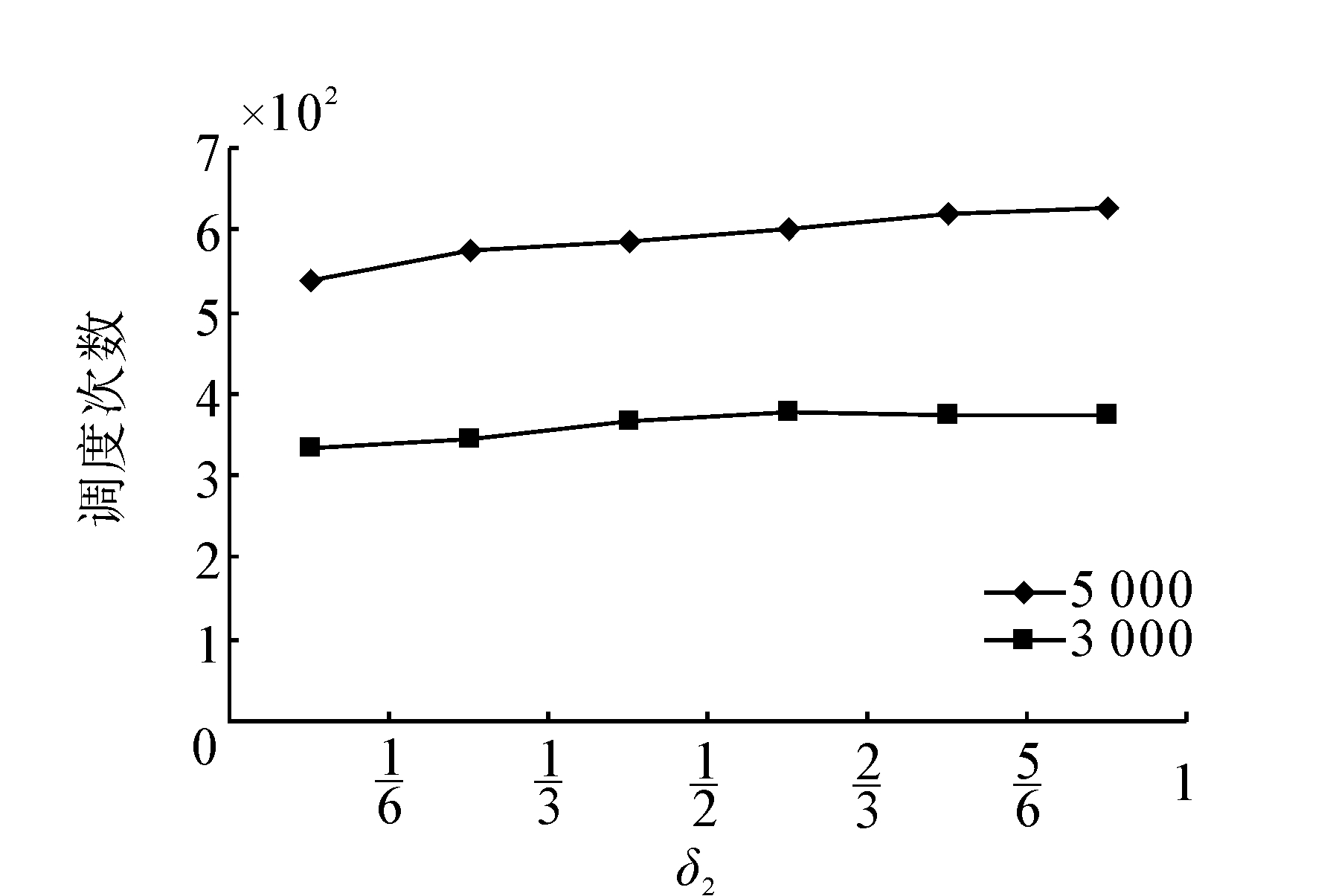 |
| 图 4 负载因子对调度次数影响Fig. 4 Change of scheduling times in the situation of different load factor |
3)实时性因子对算法性能影响
STDS算法设立实时性因子主要是解决就绪任务长时间得不到内核资源的“饥饿”现象。由式(6)可知,任务优先级是任务等待时间、任务间通信和内核负载3种因素共同决定的,通过实时性因子可以调节等待时间因素的重要程度,实时性因子反映了系统对等待时间的容忍程度。表 2是在β取不同值时对STDS算法平均等待时间和总运行时间的影响,其中AWT(average of wait time)表示平均等待时间,此时设置l=6,δ1=1/3,δ2=2/3以消除其他因素影响。由表 2可以看出,随着β值的增大,等待时间最大的100个任务的平均等待时间减小,而全部任务的平均等待时间的趋势不能确定,因为此时通信开销不是最小的,所以算法总执行时间增大,从而会造成某些任务的等待时间增大。在β取较大值(>2.0)时,STDS算法性能基本不再变化,此时STDS算法近似于先来先服务(FIFO)算法。所以β应取满足系统对实时性要求前提下的最小值。
| β | AWT of Top 100/ms | AWT of All/ms | 运行时间/ms |
| 0 | 7 603.11 | 689.446 | 32 562 |
| 0.4 | 6 752.75 | 1 084.344 | 34 250 |
| 0.8 | 6 179.30 | 901.595 | 34 922 |
| 1.0 | 4 838.11 | 882.158 | 35 125 |
| 2.0 | 4 517.32 | 911.572 | 35 756 |
| 5.0 | 4 497.84 | 926.485 | 35 998 |
综上所述,参数会对算法的调度时间、调度次数、负载均衡效果以及实时性产生影响,对于不同应用环境,应适当调整参数大小,在满足系统要求前提下充分发挥算法性能。对于实时性要求不严格系统,可以减少实时因子大小,降低总调度时间;对于规模较大系统,应增大调度粒度在减小调度次数,尽量减少调度器的调度压力,适当增大负载下限因子,保证在调度器调度不及时情况下,内核依然有充足的任务可以执行;反之亦然。本文没有明确参数值的具体大小,此工作需要通过大量具体的实际实验完成。
4.2 算法对比实验为有效评价STDS算法性能,将其与Min-Min算法和文献[11]的Vinay算法进行比较。对于每个固定的内核数,通过TGFF工具随机产生10组5000节点的DAG图,记录其调度执行时间,然后求出其平均值。由于内核数目改变,系统模型发生变化,所以实验时适当调节STDS算法参数,以充分发挥算法性能,表 3是不同内核数目时STDS算法参数取值,内核数目较多时,增大调度粒度l,虽然负载均衡效果有所下降,但降低了调度次数。图 5是STDS算法、Min-Min和Vinay算法在不同内核数目下执行时间的比较结果。
| 内核数目 | l | δ1 | δ2 | β |
| 2 | 3 | 1/3 | 2/3 | 0.1 |
| 4 | 4 | 1/2 | 1/2 | 0.1 |
| 8 | 6 | 1/3 | 2/3 | 0.1 |
| 16 | 6 | 1/2 | 1/2 | 0.1 |
| 32 | 10 | 3/10 | 7/10 | 0.1 |
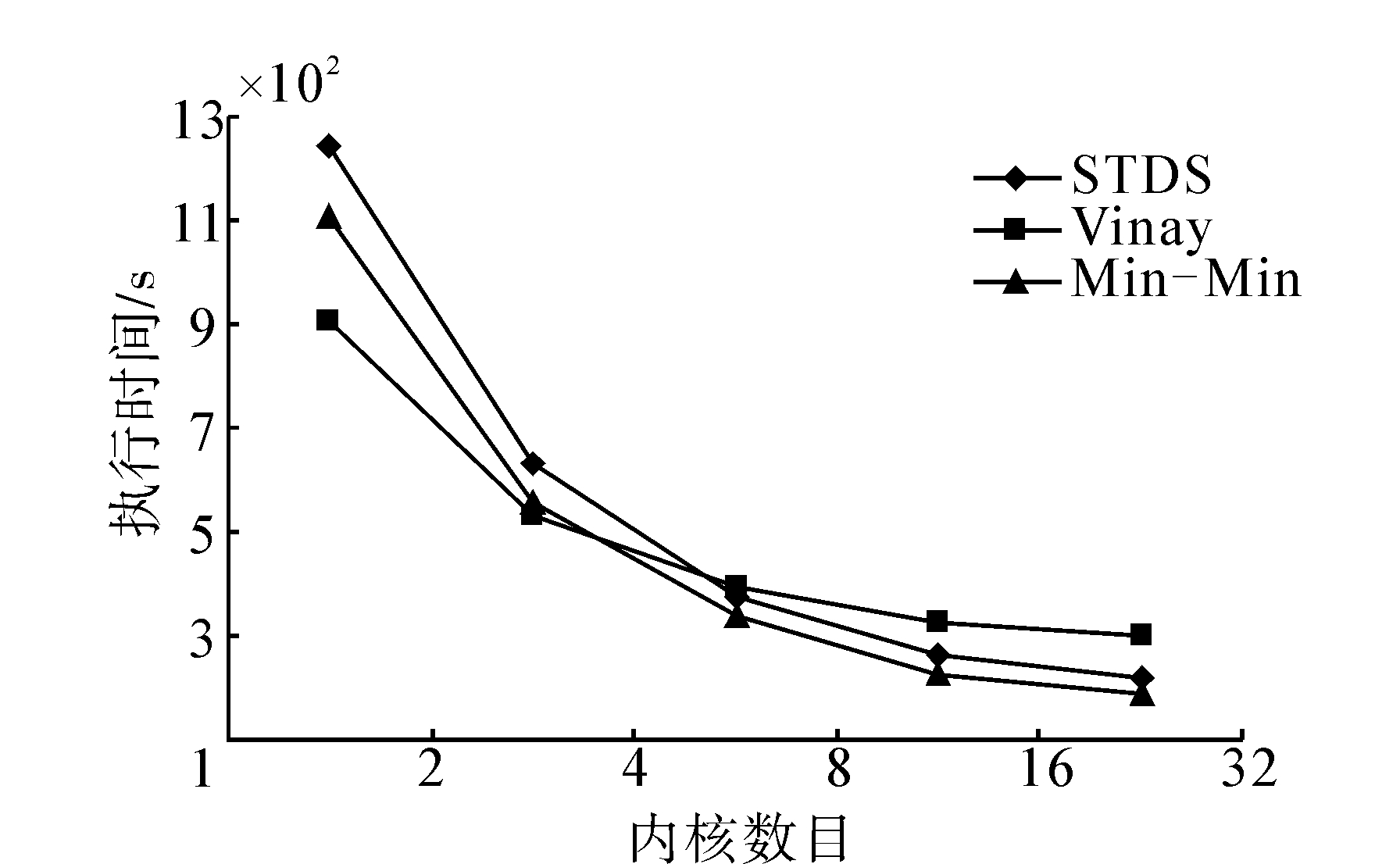 |
| 图 5 STDS、Min-Min、Vinay算法执行时间Fig. 5 Comparison of running time among STDS,Min-Min andVinay |
由图 5可以看出在内核数目较少时,Vinay算法比较高效,这是因为Vinay算法实现简单,算法复杂度低,每个内核分配一个任务,不需要考虑负载均衡等问题。随着内核数目增加,STDS算法优势逐步体现,这是因为Vinay算法一次调度分配一个任务,调度较频繁,内核数目较多时,会发生多个内核同时请求调度,但同一时刻只有一个内核可以调度成功,其他内核不得不等待。STDS算法为每个内核设置一个任务队列,每次调度会分配若干个任务,这样虽然增大了算法复杂度,但减少了调度次数且最大限度避免了内核等待现象,所以总时间较小。STDS算法比较适合内核数目较多的系统,但值得注意的是在内核数目较多的系统中,对任务量的要求也较大,否则难以充分发挥多核系统和STDS算法性能。
STDS算法复杂度与Min-Min算法相当,但调度运行时间比Min-Min算法稍长,原因是Min-Min算法将运行时间作为其唯一考虑因素,优先选取最早完成时间最小的任务进行调度。但Min-Min算法中执行时间较长的任务得不到及时执行,图 6是STDS算法与Min-Min算法等待时间的对比结果。
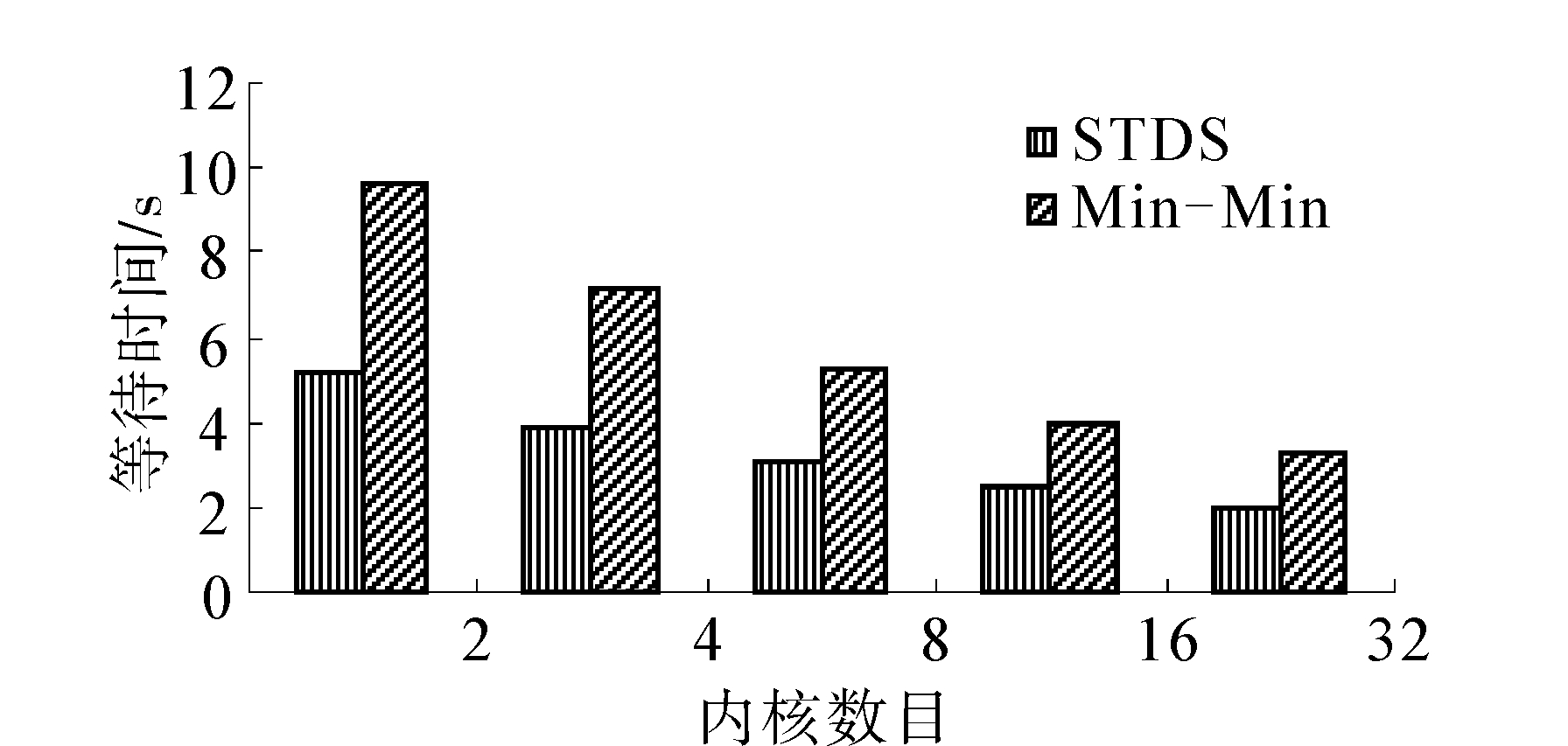 |
| 图 6 STDS算法与Min-Min算法等待时间对Fig. 6 Comparison of waiting time between STDS and Min-Min |
可以看出STDS算法中任务最大等待时间明显小于Min-Min算法。由此也可以得出STDS算法的另一大优势,就是可以通过调整参数取值,从而适应不同的系统要求。 为了排除偶然因素影响,本文通过生成另外9组不同结构的3 000 个节点与5 000个节点的DAG图,进行相同的实验,实验结果与上述描述吻合。
5 结束语文中研究了异构多核动态任务调度算法,结合设计的调度模型,提出了动态任务调度STDS算法。该算法分析了调度粒度对任务调度的影响可以根据当前内核负载和任务状态调整任务优先级,从而将高优先级的任务合理高效地分配到内核,并通过限定内核任务队列的上下限值达到负载均衡的目的。通过引入实时性因子使任务总能及时得到执行处理,减少了过长的等待时间。实验表明,STDS算法在内核较大情况下效率较高,且能够保持负载均衡。
| [1] | GENG X, XU G, ZHANG Y. Dynamic load balancing scheduling model based on multi-core processor[C]//2010 Fifth International Conference on Frontier of Computer Science and Technology (FCST). [S.l.],2010: 398-403. |
| [2] | GRAY M R, JOHNSON D S. Computers and intractability: a guide to the theory of NP-completeness[M]. New York: W H Freeman and Company, 1979: 92-115. |
| [3] | JIN H, CHEN H, CHEN J, et al. Real-time strategy and practice in service grid[C]// Proceedings of the 28th Annual International on Computer Software and Applications Conference, 2004.2004: 161-166. |
| [4] | HE X S, SUN X H,VON LASZEWSKI G . A QoS guided scheduling algorithm for grid computing[J]. Journal of Computer Science and Technology, 2003,18(4): 442-451. |
| [5] | FREUND R F, GHERRITY M, AMBROSIUS S, et al. Scheduling resources in multi-user, heterogeneous, computing environments with SmartNet[C]//Proceedings on Heterogeneous Computing Workshop. , 1998: 184-199. |
| [6] | ARMSTRONG R, HENSGEN D, KIDD T. The relative performance of various mapping algorithms is independent of sizable variances in run-time predictions[C]//Proceedings on Heterogeneous Computing Workshop. , 1998: 79-87. |
| [7] | 石威, 郑纬民. 相关任务图的均衡动态关键路径调度算法[J]. 计算机学报, 2001, 24(9): 991-997.SHI Wei, ZHENG Weimin. The balanced dynamic critical path scheduling algorithm of dependent task graph[J]. Chinese Journal of Computers, 2001, 24(9): 991-997. |
| [8] | 李仁发, 刘彦, 徐成. 多处理器片上系统任务调度研究进展评述[J]. 计算机研究与发展, 2008, 45(9): 1620-1629.LI Renfa, LIU Yan, XU Cheng. A survey of task scheduling research progress on multiprocessor system-on-chip[J]. Journal of Computer Research and Development, 2008, 45(9): 1620-1629. |
| [9] | 耿晓中. 基于多核分布式环境下的任务调度关键技术研究[D]. 吉林: 吉林大学, 2013: .GENG Xiaozhong. Research on key techniques of task scheduling based on multi-core distributed environment[D]. Jilin: Jilin University, 2013. |
| [10] | 徐雨明,李肯立. 异构系统中DAG任务调度的双螺旋结构遗传算法[J]. 计算机研究与发展,2014,51(6): 1240-1252.XU Yuming, LI Kenli. A structure genetic algorithm for task scheduling double-helix on heterogeneous computing systems [J]. Journal of Computer Research and Development, 2014, 51(6): 1240-1252. |
| [11] | VAIDYA V G, RANADIVE P, SAH S. Dynamic scheduler for multi-core systems[C]// International Conference on Software Technology and Engineering, 2010 2nd.Puerto Rico: IEEE, 2010, 1: V1-13-V1-16. |
| [12] | 陈锐忠,齐德昱,林伟伟.一种面向非对称多核处理器的综合性调度算法. 软件学报, 2013, 24(2): 34-3357.CHEN Ruozhong, QI Deyu, LIN Weiwei. Comprehensive scheduling algorithm for asymmetric multi-core processors[J]. Journal of Software, 2013, 24(2): 34-3357. |
| [13] | 邓晓衡, 卢锡城, 王怀民. iVCE中基于可信评价的资源调度研究[J]. 计算机学报, 2007, 30: 1750-1762.DENG Xiaoheng, LU Xicheng, WANG Huaimin. Study on trust evaluation based resource scheduling in iVCE[J]. Chinese Journal of Computers, 2007, 30: 1750-1762. |
| [14] | KWOK Y K, AHMAD I. Benchmarking the task graph schedulingalgorithms[C]//Parallel Processing Symposium, 1998. IPPS/SPDP 1998. Proceedings of the First Merged International... and Symposium on Parallel and Distributed Processing 1998. IEEE, 1998: 531-537. |
| [15] | FORSGREN D, ESKILSON J, CHRISTENSSON M, et al. Simics:a full system simulation platform[J]. IEEE Computer, 2002, 35(2): 50-58. |



