, ,
, ,
近年来，随着社会的发展和大数据时代的到来，人们对科技产品的能耗和性能要求越来越高，使得产品的设计遇到了极大的挑战。许多产品的设计需要考虑很多的设计要求，并要使其产品整体设计能够达到最优,这些问题都可转化为大规模复杂优化问题(optimization problems,OP)。对于OP问题，近年来，研究者将关注的焦点集中在模拟自然的启发式(meta-heuristics)优化方法[1, 2, 3, 4, 5, 6, 7, 8, 9]等。
和声搜索算法是Geem等[1]在2001年通过模拟音乐家创作音乐和调节和声的过程，提出的一种新的启发式优化算法。音乐家在音乐创作过程中，需要不断调整各个音符，使其成为优美和声。由于和声算法搜索能力强，并且结构简单，很容易在各种软件和硬件中实现，引起很多科学研究者和工程设计人员的关注，近年来，已经广泛应用于实践中，例如，管网优化设计[10]、结构优化设计[11]、交通运输路径优化[12]、电力系统经济负荷分配问题[13]和PID控制器优化[14]等领域。然而，研究发现，在有限的时间内，和声搜索算法具有很强的全局探索能力，但是，在实数优化问题中，求解精度较低[15, 16, 17]。为此，很多改进的和声搜索算法被提出，潘全科等[15]采用动态子种群策略提出了局部最好和声搜索算法，利用自适应动态策略提出一种全局最优和声搜索算法[16]。M. Mahdavi 等设计出一种参数动态调整策略，有效改进了HS算法的性能(IHS)[18]；M.G.H.Omran提出全局最优和声搜索算法(GHS)[19]； Zou [20]采用一种很简单的差分学习策略，有效屏蔽了参数HMCR (harmony memory considering rate )和 PAR(pitch-adjusting rate)，降低了算法的复杂性[21, 22]。P.Yadav 给出一种智能调整和声搜索算法(ITHS)[17]; S.Das通过理论分析与证明，给出了一种新的和声步长(pitch bandwidth，BW)调整算法(EHS)[23]；本文作者在文献[24]和[25]中分别提出了“混沌和声搜索算法”与“基于教与学策略的和声搜索算法”;另外，在一些具体应用中，对和声搜索算法进行了有效改进[26, 27, 28, 29, 30, 31, 32, 33, 34]。尽管上述改进算法从某些方面对和声搜索算法进行了改进，但并没有从算法的运行代价考虑，比如EHS算法，虽然搜索能力有了明显的改进，但是，由于每次迭代都需要计算和声记忆库(harmony memory，HM)的方差，其计算量甚至超过了和声搜索算法本身的计算量，使得算法的运行代价是标准和声算法HS的好几倍。特别是在求解高维复杂优化问题时，目前的和声算法运行速度普遍较慢。为此，本文通过引入一种动态和声调整策略，使其能够有效提高和声算法的性能，并且，能使算法运行代价降低，提高其搜索速度。
1 标准和声搜索算法考虑如下优化问题：
标准和声搜索算法的基本步骤如下：
1)设置参数值(D,HMS,Tmax,HMCR,PAR,BW)。各参数含义如下：
D为问题的维数，HMS为和声记忆库大小，Tmax 为算法迭代次数；HMCR为和声记忆库选择概率，PAR为局部微调概率，BW为局部微调步长值。
2)随机初始化和声记忆库HM
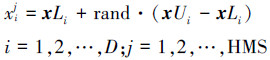
3)利用3种和声调节规则创作新和声
通过如下3个规则产生新和声 xnew=[x1new x2new … xDnew] 。
①和声记忆库选择。新和声向量xnew的决策变量xinew(i=1,2,…,D) 以概率HMCR从和声记忆库的第i维[xi1 xi2 … xiHMS]T中随机选取。
②局部微调。局部微调是将①中产生的xinew(i=1,2,…,D)以概率PAR进行再次微调。微调方法如下：
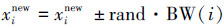
③搜索空间内随机产生。新和声向量xnew的决策变量xinew(i=1,2,…,D) 以概率1-HMCR在搜索空间内随机产生。产生方法如下：
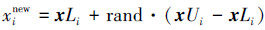
4)更新操作
如果新和声向量xnew优于HM中最差的和声xworst，则用xnew 将其替换，否则，转至(3)重新产生新和声。重复3)、4)，直到满足终止条件。
2 动态降维和声调整策略 2.1 2种和声调整策略分析与比较目前的和声搜索算法和一些改进算法是在整个种群的基础上通过组合策略(规则①)产生新的候选解，这样实现了组合算子的多样性，因此具有较好的全局搜索性能。但是，在进化后期，即使发现了全局最优解所在的区域，由于其较低的更新成功率(更新成功率是指每次产生的新解好于和声记忆库中最差解的概率)，使得算法往往很难获得高精度的最优解。
对于一个高维优化问题，必然要从大范围的扰动开始逐步到小范围(部分维度)的微调，最终使其在所有维上都能够达到最优，然而，和声优化算法在进行优化时，总是通过组合算子产生一个全新的个体xnew，然后与和声记忆库HM中最差个体xworst 比较其优劣性，决定是替换还是丢弃。假设某一D维优化问题的最优解为 [x1* x2* … xD*] ，利用和声搜索算法对其进行优化，开始时，随机初始化后的和声记忆库HM如式(1)，经过一段时间优化后，HM变为式(2)，
此时，假设HM的每个和声中都仅有一个决策变量没有达到最优。由于和声算法中规则①的调整概率HMCR一般都大于0.9，也就是说规则①在和声搜索算法中是非常重要的，这时，如果仅仅采用和声搜索算法中的规则①进行优化。采用下列2种方法分别产生一个新和声 xnew ，分析2种方法的更新成功率。
1)如果完全利用规则①产生一个新和声xnew=[x1* x2* … xD*]。那么，xinew(i=1,2,…,D)取到xi*(i=1,2,…,D)的概率为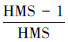
，则xnew=[x1* x2* … xD*]的概率为
。
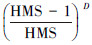2)选取HM中一个和声作为调整目标，然后，随机的将其中某一决策变量利用规则①重新生成。假设选取x1作为优化调整目标xnew,则xnew=[y1 x2* x3* … xD*]，随机选取一个决策变量进行调整，选取到y1的概率为1/D,并且利用规则①能够将其调整为x1* 的概率为(HMS－1)/HMS,因此，优化调整后，xnew=[x1* x2* … xD*]的概率为(1/D)·((HMS－1)/HMS)。
假设HMS=10,D=10，则利用方法1得到最优解xnew=[x1* x2* … xD*]的概率为
，利用方法2得到最优解的概率为(1/D)·((HMS－1)/HMS) =0.09，显然此时，方法1更容易得到最优解。但是，当HMS=10,维度D=100时，方法1得到最优解的概率为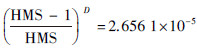
，利用方法2得到最优解的概率为(1/D)·((HMS－1)/HMS) =0.009，显然，方法2具有更高的成功率。图 1给出2种方法的成功率变化曲线。
 |
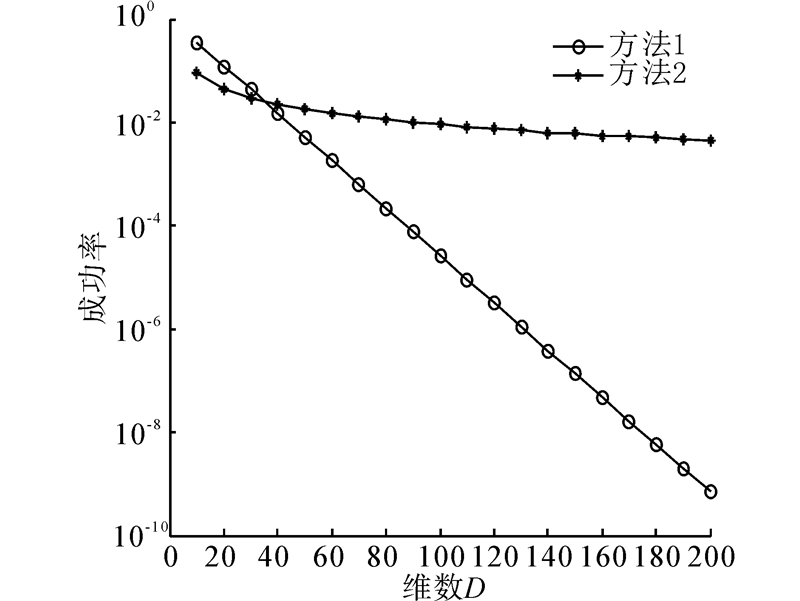| 图 1 2种方法在维数不同时的更新成功率曲线图 Fig. 1 The update-success rate curve of two methods on different dimensioalities |
图 1可以看出，在HMS相同的情况下，随着维数D的增加，方法1的成功率急剧下降，而方法2下降幅度很小。在问题的维数较低时，方法1的更新成功率高于方法2，但当维数D＞40时，方法2的更新成功率高于方法1。
由上例可知，对于一个高维优化问题，利用方法1难以驱动算法获得高精度的最优解。如果借鉴方法2的思想进行优化，就有可能取得较好的优化效果。因此，本文提出一种基于动态减少调整维数的和声优化策略。该策略首先选取和声记忆库中最差和声向量作为优化目标，然后，通过对最差和声向量的不断调整，使其达到最优解。在优化刚开始时，对最差和声向量进行较多维数的扰动，使得算法具有较强的空间探索能力，随着优化的进行，逐步降低扰动概率，仅仅在较少维上进行优化调整，使得优化调整具有更高的成功率，从而获得高精度的全局最优解。
2.2 基于动态降维调整的和声搜索算法本文提出的基于动态降维调整策略的和声搜索算法流程请见图 2。本文算法中，调整概率TP=TPmax－(TPmax－TPmin)·(t/Tmax)2随着迭代次数的增加逐步减小(如图 3)，其中，TPmax和TPmin 分别为最大调整概率值和最小调整概率值。
 |
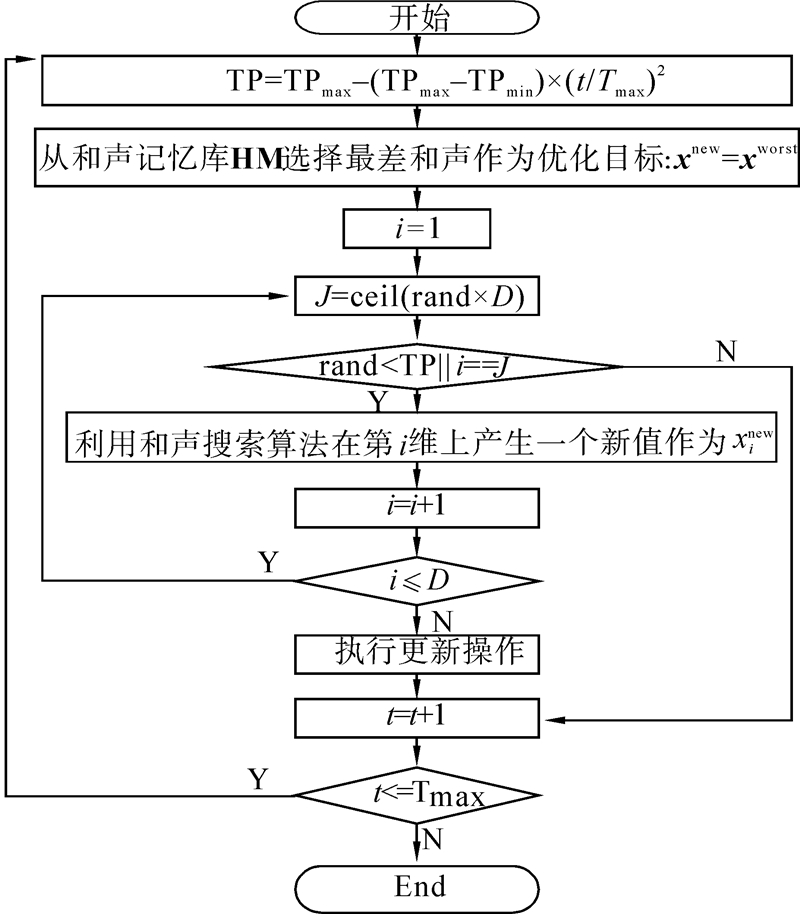| 图 2 基于动态降维调整的和声搜索算法流程图 Fig. 2 The flow chart of HS algorithm based on dynamic dimensionality reduction strategy |
 |
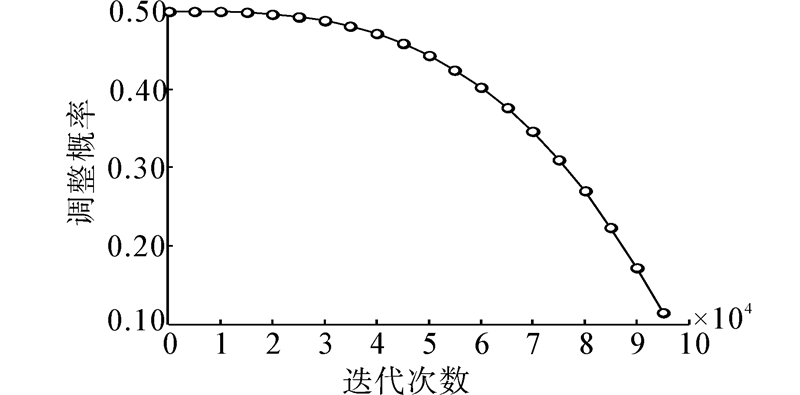| 图 3 调整概率TP变化曲线 Fig. 3 Adjustment curve of TP |
在算法优化开始时，以较大的扰动调整概率TPmax进行优化，随着优化进行，调整概率TP逐渐减小，开始进行局部微调。但是，为了防止优化调整概率太小，可能导致所有维都得不到调整，因此，需要从1~D中随机选取一维J=ceil(rand×D) ，使其必须得到调整，避免了算法“空转”。这样调整的好处是，迭代初期，需要较强的全局扰动能力，此时，可以在优化目标向量xnew 上加大扰动力度，增强种群多样性，使其具有较强的全局探索能力，随着优化的进行，到了后期，多数个体可能已经聚集在了全局最优解附近，此时，开始加强局部最优解的探索，为了保证较高的更新成功率，对优化目标向量xnew ，选择较少的维数进行优化调整，从而，增强算法的求解精度。
3 仿真实验为了评估本文算法提出的动态降维调整策略的性能，选取了6个复杂的Benchmark测试函数进行仿真测试[35, 36, 37, 38](见表 1)，16个函数除了F7和F8 是单峰函数之外，其余函数都是复杂的高维多峰值函数。
| 函数名称 | Benchmark函数表达式 | 搜索范围 | 参数值 |
| F1 Ackley Function | 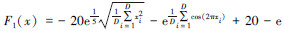 | [－15,30]D | x*=(0,0,…,0) F1(x*)=0 |
| F2 Griewank Function | 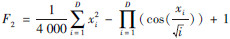 | [－600,600]D | x*=(0,0,…,0) F2(x*)=0 |
| F3Levy Function | 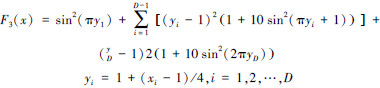 | [－10,10]D | x*=(1,1,…,1) F3(x*)=0 |
| F4Michalewics Function | 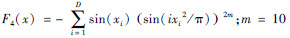 | [－10,π]D | n=5 F4(x*)=－4.687 658 |
| F5Rastrigin Function | 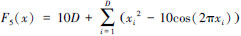 | [－5.12,5.12]D | x*=(0,0,…,0) F5(x*)=0 |
| F6Schwefel 2.26 Function | 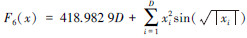 | [－512,512]D | x*=(420.968 7, 420.968 7,…,420.968 7) F6(x*)=0 |
分别将HS、IHS、ITHS、EHS和GHS利用本文算法思想进行改进，将其改进后分别称为HS2，IHS2，ITHS2，EHS2和GHS2，并将其与改进前的算法进行比较。检验改进后的算法是否比改进前的算法能够获得更高精度的解，同时，检验其运行成本(运行时间)是否降低。
3.1 实验环境和算法参数设置本文实验采用戴尔工作站T7500 Inter(R) Xeon(R) CPU E560@ 2.1 GHz,8.0 GB内存，Windows Server2003 Server操作系统，所有测试程序采用Matlab R2009a编写。10种算法参数设置如表 2。
| 算法 | HMS | HMCR | PAR | BW | TP |
| HS | 10 | 0.99 | 0.33 | (xU-xL)/2 000 | / |
| HS2 | 10 | 0.99 | 0.33 | (xU-xL)/2 000 | TPmax=0.6，TPmin=5/D |
| IHS | 10 | 0.99 | PARmax=0.99,PARmin=0.1 | BWmax=(xU-xL)/20 | / |
| BWmin=(xU-xL)/(1e+8) | |||||
| IHS2 | 10 | 0.99 | PARmax=0.99,PARmin=0.1 | BWmax=(xU-xL)/20 | TPmax=0.6，TPmin=5/D |
| BWmin=(xU-xL)/(1e+8) | |||||
| GHS | 10 | 0.90 | PARmax=0.99,PARmin=0.01 | / | / |
| GHS2 | 10 | 0.90 | PARmax=0.99,PARmin=0.01 | / | TPmax=0.6，TPmin=5/D |
| EHS | 50 | 0.99 | 0.33 | / | / |
| EHS2 | 50 | 0.99 | 0.33 | / | TPmax=0.6，TPmin=5/D |
| ITHS | 10 | 0.99 | PARmax=1,PARmin=0 | / | / |
| ITHS2 | 10 | 0.99 | PARmax=1,PARmin=0 | / | TPmin=0.6，TPmin=5/D |
为了保证算法测试的公平性，改进前的算法和改进后的算法取相同的初始和声记忆库HM，每个算法中随机数设置rand(′twister′,5 489)，每个算法程序独立运行20次，记录每次运行的过程，统计出20次运行的最优目标函数适应值的平均值Mean，最优值Best,20次最优解的标准差(Std)和平均运行时间(run time)。设置维数 D =500，运行结果见表 3。表中将HS、IHS、ITHS、EHS和GHS 分别与HS2、IHS2、ITHS2、EHS2和GHS2进行比较，较好结果的用粗体标出。
| 算法 | F 1 | F 2 | F 3 | |||||||||
| Best | Mean | Std | Runtime | Best | Mean | Std | Runtime | Best | Mean | Std | Runtime | |
| HS | 2.34×10 0 | 2.50×10 0 | 6.67×10 -2 | 2.52×10 2 | 6.32×10 -1 | 6.75×10 -1 | 2.39×10 -2 | 3.06×10 2 | 8.04×10 -2 | 9.70×10 -2 | 1.80×10 -2 | 1.61×10 3 |
| HS 2 | 1.39×10 -1 | 1.61×10 -1 | 1.14×10 -2 | 1.89×10 2 | 4.20×10 -1 | 5.31×10 -1 | 8.25×10 -2 | 2.48×10 2 | 1.09×10 -4 | 1.24×10 -4 | 7.07E-06 | 1.53×10 3 |
| GHS | 1.57×10 1 | 1.64×10 1 | 2.75×10 -1 | 2.67×10 2 | 1.88×10 3 | 2.11×10 3 | 1.49×10 2 | 3.45×10 2 | 7.11×10 2 | 7.96×10 2 | 4.40×10 1 | 9.03×10 2 |
| GHS 2 | 1.24×10 -2 | 4.29×10 -2 | 2.86×10 -2 | 2.42×10 2 | 9.85×10 -3 | 2.83×10 -1 | 2.72×10 -1 | 3.06×10 2 | 1.30×10 -3 | 8.25×10 -3 | 9.63×10 -3 | 8.86×10 2 |
| IHS | 6.57×10 -1 | 1.10×10 0 | 1.74×10 -1 | 3.79×10 2 | 5.92×10 -2 | 7.60×10 -2 | 8.85×10 -3 | 4.64×10 2 | 5.27×10 -2 | 1.05×10 -1 | 4.09×10 -2 | 1.24×10 3 |
| IHS 2 | 8.71×10 -7 | 8.81×10 -7 | 6.81×10 -9 | 3.16×10 2 | 2.69×10 -11 | 3.70×10 -4 | 1.65×10 -3 | 4.00×10 2 | 1.17×10 -12 | 1.19×10 -12 | 2.75×10 -14 | 9.71×10 2 |
| ITHS | 7.90×10 -3 | 2.95×10 -2 | 1.18×10 -2 | 3.17×10 2 | 6.41×10 -3 | 1.92×10 -1 | 9.97×10 -2 | 3.87×10 2 | 1.35×10 -3 | 4.75×10 -3 | 2.16×10 -3 | 1.70×10 3 |
| ITHS 2 | 1.50×10 -13 | 3.49×10 -13 | 1.75×10 -13 | 2.16×10 2 | 6.66×10 -16 | 7.72×10 -16 | 5.67E-17 | 2.62×10 2 | 1.50×10 -32 | 1.50×10 -32 | 0.00×10 0 | 1.62×10 3 |
| EHS | 4.55×10 0 | 4.70×10 0 | 8.66×10 -2 | 5.02×10 2 | 2.12×10 1 | 2.47×10 1 | 1.58×10 0 | 5.75×10 2 | 1.11×10 2 | 1.26×10 2 | 7.58×10 0 | 2.04×10 3 |
| EHS 2 | 2.71×10 -13 | 2.21×10 -5 | 6.85×10 -5 | 4.32×10 2 | 7.77×10 -16 | 1.26×10 -5 | 5.38×10 -5 | 5.17×10 2 | 3.54E-15 | 1.25×10 -7 | 3.96×10 -7 | 1.24×10 3 |
| 算法 | F 4 | F 5 | F 6 | |||||||||
| Best | Mean | Std | Runtime | Best | Mean | Std | Runtime | Best | Mean | Std | Runtime | |
| HS | -2.08×10 2 | -2.01×10 2 | 4.92×10 0 | 6.48×10 2 | 1.10×10 2 | 1.26×10 2 | 1.07×10 1 | 3.21×10 2 | 4.57×10 1 | 4.95×10 1 | 2.42×10 0 | 2.98×10 2 |
| HS 2 | -4.28×10 2 | -4.26×10 2 | 2.03×10 0 | 5.25×10 2 | 1.13×10 -2 | 1.28×10 -2 | 8.39×10 -4 | 2.03×10 2 | 6.99×10 -2 | 8.04×10 -2 | 6.73×10 -3 | 2.15×10 2 |
| GHS | -2.26×10 2 | -2.22×10 2 | 2.90×10 0 | 5.22×10 2 | 1.61×10 3 | 1.90×10 3 | 1.19×10 2 | 3.50×10 2 | 3.35×10 4 | 3.81×10 4 | 2.16×10 3 | 3.47×10 2 |
| GHS 2 | -2.65×10 2 | -2.62×10 2 | 1.55×10 0 | 4.98×10 2 | 8.81×10 -4 | 1.10×10 -1 | 1.69×10 -1 | 3.14×10 2 | 1.54×10 -2 | 1.26×10 0 | 1.51×10 0 | 3.23×10 2 |
| IHS | -4.55×10 2 | -4.53×10 2 | 2.43×10 0 | 6.36×10 2 | 1.02×10 2 | 1.17×10 2 | 5.45×10 0 | 4.99×10 2 | 6.66×10 0 | 4.63×10 1 | 3.27×10 1 | 4.56×10 2 |
| IHS 2 | -4.98×10 2 | -4.97×10 2 | 1.33×10 -1 | 5.83×10 2 | 1.71×10 -2 | 1.20×10 -1 | 1.05×10 -1 | 4.16×10 2 | 1.37×10 -9 | 1.47×10 -9 | 6.97×10 -11 | 3.83×10 2 |
| ITHS | -4.51×10 2 | -4.42×10 2 | 3.69×10 0 | 5.96×10 2 | 4.35×10 -3 | 5.94×10 -2 | 5.25×10 -2 | 4.38×10 2 | 6.79×10 2 | 1.39×10 3 | 5.00×10 2 | 5.66×10 2 |
| ITHS 2 | -4.98×10 2 | -4.98×10 2 | 3.11×10 -1 | 4.89×10 2 | 1.18×10 -11 | 4.27×10 -11 | 3.71×10 -11 | 2.97×10 2 | 1.39×10 -9 | 2.85×10 -10 | 3.98×10 2 | |
| EHS | -1.63×10 2 | -1.58×10 2 | 1.99×10 0 | 8.64×10 2 | 4.43×10 3 | 4.52×10 3 | 4.70×10 1 | 6.68×10 2 | 1.27×10 5 | 1.32×10 5 | 1.78×10 3 | 6.48×10 2 |
| EHS 2 | -4.43×10 2 | -4.41×10 2 | 1.38×10 0 | 8.10×10 2 | 3.84×10 2 | 4.52×10 2 | 2.89×10 1 | 5.90×10 2 | 2.36×10 4 | 2.61×10 4 | 1.33×10 3 | 5.38×10 2 |
从表 3可看出，对于高维多峰值优化函数(例如，F3: Levy,F5: Rastrigin,F6:Schwefel2.26)，本文算法相比改进前的算法，更具有优势，算法的运行代价(运行时间)也相对较少。说明本文算法在求解高维多极值复杂优化问题时具有更好的性能优势。
3.3 算法更新成功率分析为了进一步分析本文提出的动态降维调整策略的性能，通过分析算法的更新成功率SuccessRate来判别算法的优劣性。更新成功率(SuccessRate)是指利用和声搜索算法产生的新解Xnew优于和声记忆库中最差解Xworst 的概率，计算方法是记录最近100次更新操作成功的次数(SuccesTimes)，让其除以总的比较次数100(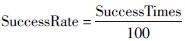
)。实验中，对多峰值函数Rastrigin进行测试，设置函数的维数 D =1 000；将改进前的算法HS、IHS、EHS和ITHS算法分别与利用本文策略改进后的算法HS2、IHS2、EHS2和ITHS2进行比较。具体成功率曲线如图 4。
 |
| 图 4 函数Rastrigin在 D =1 000时，改进前与改进后的算法成功率比较 Fig. 4 Successrate comparison between ITHS and improved ITHS on D =1 000 |
由图 4可以看出，本文策略改进后的算法成功率都明显高于改进前的算法，并且，改进后的算法成功率曲线成凹形曲线变化。这是由于初始时，种群是随机产生，个体的适应值较差，容易探索到比当前更好的解。随着迭代的进行，成功率逐渐降低。对改进前的算法来说，由于一个新解完全是靠组合算子和微调策略产生，成功率会越来越低(根据第3节的分析)，而本文采用动态降维调整策略逐步减小最差解 xworst 中决策变量的调整概率，从而增加了更新成功率。从图 4中可以看出，在后期，算法的成功率不降反升，证明了本文改进策略的有效性。这是由于在后期，只对最差解向量 xworst 中很少的几个决策变量进行调整，获得成功的机会远高于在所有维上的更新调整。
3.4 算法种群多样性分析种群的多样性是指种群中个体间的差异性，个体差异越大，种群多样性越高，反之，差异性越小，种群多样性越低。本文采用如下公式计算种群的多样性。
，
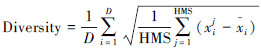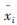是和声记忆库HM中第i维的平均值。
对于群智能优化算法来说，种群的多样性直接决定算法的搜索能力，当具有较高的种群多样性时，算法的全局探索能力较强，适合探索新的搜索区域，但是，如果一直保持较高的种群多样性，种群很难向全局最优解靠近，往往难以获得高精度的全局最优解。所以，在搜索初期，需要种群具有较高的种群多样性，后期，为了获得高精度的全局最优解，种群需要向最优解聚集，多样性逐步降低。
和声搜索算法具有较强的全局探索能力，但求解精度较低[19, 20],主要是因为在进化后期，算法的局部求解能力较差。本文通过对多峰值函数Schwefel2.26进行测试(设置函数的维数 D =1 000)，比较改进后的与改进前算法中种群多样性的变化(如图 5)。
 |
| 图 5 函数Schwefel 2.26的多样性曲线( D =1 000) Fig. 5 diversity curve of function Schwefel2.26 ( D =1 000) |
图 5可以看出，改进后算法种群多样性变化明显，在搜索初期，多样性较高，有助于进行全局探索，随着搜索的进行，当种群逐渐聚集到全局最优解附近区域时，开始进行局部高精度求解，种群的多样性迅速降低。
4 结束语本文提出用一种新颖的维度动态调整策略改进和声搜索算法，使其通过对和声记忆库中最差和声向量进行调整，在优化初期，采用大范围、广维度调整策略保证了种群的多样性，增强了算法的全局探索能力；随着优化的进行，逐步降低调整维数，慢慢变为在部分维上进行调整，从而增强算法的局部开发能力，提高其求解精度。这样，和声搜索算法有效地在全局探索和局部开发之间实现了平衡. 通过对6个高维复杂多极值测试函数进行实验，发现本文算法在求解精度和运算成本上都有了明显改进，并且，随着维数的增加，本文算法的优势更加显著，说明本文改进策略可用于大规模高维复杂问题的求解。
| [1] | GOLDBERG D E. Genetic algorithms in search optimization and machine learning[M]. Boston: Addison-Wesley, 1989:25-30. |
| [2] | EBERHART R C, KENNEDY J. A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Nagoya, Japan, 1995: 23-30. |
| [3] | STORN R, PRICE K V. Minimizing the real functions of the ICEC 1996 contest by differential evolution[C]//Proc IEEE Int Conf Evol Comput. Nagoya, Japan, 1996: 842-844. |
| [4] | DORIGO M, MANIEZZO V, COLORNI A. The ant system: optimization by a colony of cooperating agents[J]. IEEE Trans Syst Man Cybern, 1996, 26(1): 29-41. |
| [5] | KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8 (1): 687-697. |
| [6] | GEEM Z W, KIM J H, LOGANATHAN G V. A new heuristic optimization algorithm: harmony search[J]. Simulation, 2001, 76: 60-70. |
| [7] | SIMON D. Biogeography-based optimization[J]. IEEE Transactions on Evolutionary Computation, 2008, 12: 702-713. |
| [8] | RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design, 2011, 43: 303-315 |
| [9] | 拓守恒,雍龙泉,邓方安. “教与学”优化算法研究综述[J]. 计算机应用研究, 2013(7): 1933-1938. TUO shouheng, YONG Longquan, DENG Fang′an. Survey of teaching-learning-based optimization algorithms[J]. Application Research of Computers, 2013(7): 1933-1938. |
| [10] | GEEM Z W, KIM J H, LOGANATHAN G V. Harmony search optimization: application to pipe network design[J]. International Journal of Modelling & Simulation, 2002, 22(2): 125-133. |
| [11] | LEE K S, GEEM Z W. A new structural optimization method based on the harmony search algorithm[J]. Computers & Structures, 2004, 82(9): 781-798. |
| [12] | GEEM Z W, LEE K S, PARK Y. Application of harmony search to vehicle routing[J]. American Journal of Applied Sciences, 2005, 2(12): 1552. |
| [13] | VASEBI A, FESANGHARY M, BATHAEE S M T. Combined heat and power economic dispatch by harmony search algorithm[J]. International Journal of Electrical Power & Energy Systems, 2007, 29(10): 713-719. |
| [14] | WANG H, YUAN X, WANG Y, et al. Harmony search algorithm-based fuzzy-PID controller for electronic throttle valve[J]. Neural Computing and Applications, 2013, 22(2): 329-336. |
| [15] | PAN Q K, SUGANTHAN P N, LIANG J J, et al. A local-best harmony search algorithm with dynamic subpopulations[J]. Engineering Optimization, 2010, 42(2): 101-117. |
| [16] | PAN Q K, SUGANTHAN P N, TASGETIREN M F, et al. A self-adaptive global best harmony search algorithm for continuous optimization problems[J]. Applied Mathematics and Computation, 2010, 216(3): 830-848. |
| [17] | YADAV P, KUMAR R, PANDA S K, et al. An intelligent tuned harmony search algorithm for optimization[J]. Information Sciences, 2012, 196: 47-72. |
| [18] | MAHDAVI M, FESANGHARY M, DAMANGIR E. An improved harmony search algorithm for solving optimization problems[J]. Applied Mathematics and Computation, 2007, 188(2): 1567-1579. |
| [19] | OMRAN M G H, MAHDAVI M. Global-best harmony search[J]. Applied Mathematics and Computation, 2008, 198(2): 643-656. |
| [20] | ZOU Dexuan, GAO Liqun, WU Jianhua, et al. Novel global harmony search algorithm for unconstrained problems[J]. Neurocomputing, 2010,73: 3308-3318. |
| [21] | ZOU Dexuan, GAO Liqun, WU Jianhua, et al. A novel global harmony search algorithm for reliability problems[J]. Computers & Industrial Engineering, 2010, 58 (2): 307-316. |
| [22] | ZOU Dexuan, GAO Liqun, LI S, et al. Solving 0-1 knapsack problem by a novel global harmony search algorithm[J]. Applied Soft Computing, 2011, 11: 1556-1564. |
| [23] | DAS S, MUKHOPADHYAY A, ROY A, et al. Exploratory power of the harmony search algorithm: analysis and improvements for global numerical optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2011, 41(1): 89-106. |
| [24] | TUO Shouheng, YONG Longquan. An improved harmony search algorithm with chaos[J]. Journal of Computational Information Systems, 2012, 8(10 ): 4269-4276. |
| [25] | TUO Shouheng, YONG Longquan, ZHOU Tao. An improved harmony search based on teaching-learning strategy for unconstrained optimization problems[J]. Mathematical Problems in Engineering, 2013, 19: 69-76. |
| [26] | SARVARI H, ZAMANIFAR K. Improvement of harmony search algorithm by using statistical analysis[J]. Artificial Intelligence Review, 2012, 37(3): 181-215. |
| [27] | ASKARZADEH A, REZAZADEH A. A grouping-based global harmony search algorithm for modeling of proton exchange membrane fuel cell[J]. International Journal of Hydrogen Energy, 2011, 36(8): 5047-5053. |
| [28] | GHOSH S, KUNDU D, SURESH K, et al. Design of optimal digital IIR fillers by using a bandwidth adaptive harmony search algorithm[C]//2009 World Congress on Nature & Biologically Inspired Computing. Coimbatore, India, 2009: 480-485. |
| [29] | HOANG D C, YADAV P, KUMAR R, et al. A robust harmony search algorithm based clustering protocol for wireless sensor networks[C]//2010 IEEE International Conference on Communications Workshops (ICC). [S.l.], 2010: 1-5. |
| [30] | JABERIPOUR M, KHORRAM E. Solving the sum-of-ratios problems by a harmony search algorithm[J]. Journal of Computational and Applied Mathematics, 2010, 234(3): 733-742. |
| [31] | POURSHA M, KHOSHNOUDIAN F, MOGHADAM A S. Harmony search based algorithms for the optimum cost design of reinforced concrete cantilever retaining walls[J]. International Journal of Civil Engineering, 2011, 9(1): 1-8. |
| [32] | KHAZALI A H, KALANTAR M. Optimal reactive power dispatch based on harmony search algorithm[J]. International Journal of Electrical Power & Energy Systems, 2011, 33(3): 684-692. |
| [33] | KHAZALI A H, PARIZAD A, KALANTAR M. Optimal voltage/reactive control by an improve harmony search algorithm[J]. Int Rev Electr Eng, 2010, 5: 217-224. |
| [34] | KHORRAM E, JABERIPOUR M. Harmony search algorithm for solving combined heat and power economic dispatch problems[J]. Energy Conversion and Management, 2011, 52(2): 1550-1554. |
| [35] | FUKUSHIMA M. Test functions for unconstrained global optimization[OL/EB]. [2014-01-12]. http://www-optima.amp.i.kyoto-u.ac.jp/member/student/hedar/Hedar-files/TestGO-files/Page364.htm. |
| [36] | TANG K, YAO X, SUGANTHAN P N, et al. Benchmark functions for the CEC’2008 special session and competition on large scale global optimization[OL/EB]. [2013-10-21].http://www.ntu.edu.sg/home/EPNSugan/, 2008. |
| [37] | TANG K, LI X, SUGANTHAN PN, et al. Benchmark functions for the CEC’2010 special session and competition on large scale global optimization[R]. Nature Inspired Computation and Applications Laboratory, USTC, China & Nanyang Technological University, 2009. |
| [38] | HERRERA F, LOZANO M, MOLINA D. Test suite for the special issue of soft computing on scalability of evolutionary algorithms and other meta-heuristics for large scale continuous optimization problems[OL/EB]. [2013-10-21].http://sci2s.ugr.es/eamhco/CFP.php. |