2. 辽宁科技大学 研究生院, 辽宁 鞍山 114051
2. Graduate School, Liaoning University of Science and Technology, Anshan 114051, China
群体机器人编队控制可以分为队形形成和队形保持,如今已经引起研究者的广泛关注,并取得了重要的理论成果。Das等[1]通过 l-ψ和l-l控制策略之间的转化来解决不同环境下队形变换问题。Defoort[2]设计了一阶和二阶滑模控制器使机器人在运动过程中保持指定队形不变。Ogren[3]通过控制Lyapunor 函数实现群体机器人系统编队控制。Marshall [4]针对轮式机器人编队问题,提出了循环追逐策略,并证明了队形的稳定性。Ren等[5, 6]针对多智能体一致性理论提出了二阶一致性协议,并结合图论理论实现机器人队形形成与保持。以上提到的控制策略各不相同,但都体现了各自的优势。同样基于系统包含原理的对对分解与分散协调控制在解决机器人编队问题也有自己独特的优势,它将一个复杂重叠互联系统重叠展开成多个成对的子系统,对每个子系统对分别设计独立的控制器与观测器以实现每个子系统对的协调控制,最终将分散协调控制器与观测器收缩回原系统实现整体的协调控制,达到简化复杂系统分析与设计的目的。如今,包含原理已经应用于多个领域,如多区域电力系统[7, 8]、自动车组系统[9]、高层建筑结构振动系统[10]等,而在群体机器人编队控制领域中特别是队形形成应用得较少,队形形成正是机器人队形控制的基础。
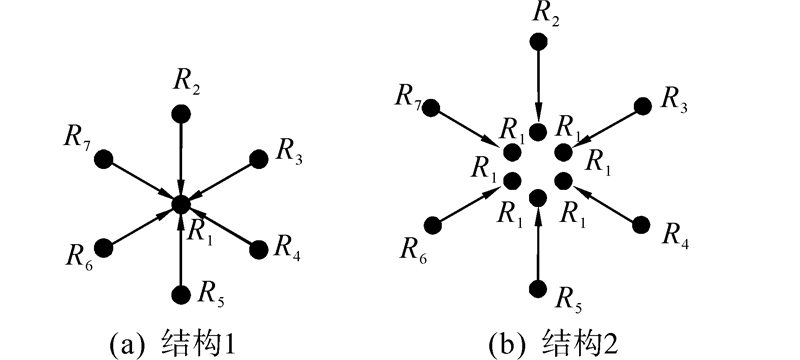
1 模型描述 1.1 机器人运动学模型构建在多种群体机器人队形中,正六边形结构队形在多群体机器人集结运动中有着独特的优势。从图 1(a)可以看出每个机器人之间的距离相等每条连接线之间的夹角为60°,成中心对称结构。当多个机器人加入其中时只需保证与相邻2个机器人之间的距离相等并等于六边形边长即可实现群体的集结,如图 1(b),同时有着稳定的结构,因此研究六边形结构队形的形成很有必要。Leader-follower是机器人队形形成最常见的方法也是最成熟的方法。因此本文基于包含原理的对对分解与分散协调控制方法,并以7个机器人为例来研究正六边形结构队形的形成和速度的一致性问题。
 |
| 图 1 正六边形结构队形 Fig. 1 Regular hexagon structural formation |
根据文献[11]机器人运动学模型可以描述为
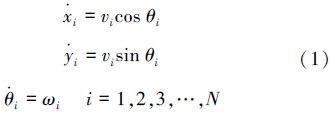


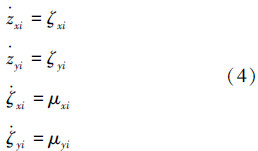
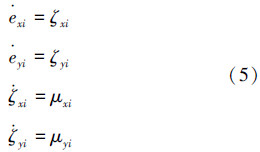
由式(5)得出第i个机器人运动学线性模型的状态空间描述:

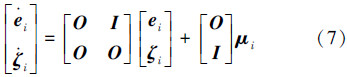
本文考虑7个机器人leader-follower系统,它的信息交换拓扑结构如图 2(a)所示,为有向图[13]。假设机器人R2、R3、R4、R5、R6、R7只能感知到R1的状态信息,而它们相互之间无法感知到对方信息。因此可以认为R1是领航者,其他6个机器人为跟随者。由此所构建的7个机器人组成的动态系统模型如式(8),同时考虑了现实系统中存在的随机噪声。
 |
| 图 2 7个机器人信息交换拓扑结构 Fig. 2 Seven robots information exchange topology |

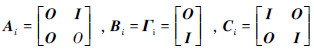 ,ξi和ηi分别为子系统输入噪声和输出测量噪声向量序列,其协方差分别为Wξi和Wηi。式(8)用虚线标出了领航者与一个跟随者组成的子系统对。即,机器人R1分别与机器人R2、R3、R4、R5、R6和R7组成一个子系统对。
2 群体机器人系统重叠结构分解
,ξi和ηi分别为子系统输入噪声和输出测量噪声向量序列,其协方差分别为Wξi和Wηi。式(8)用虚线标出了领航者与一个跟随者组成的子系统对。即,机器人R1分别与机器人R2、R3、R4、R5、R6和R7组成一个子系统对。
2 群体机器人系统重叠结构分解
系统包含原理是解决具有信息结构约束系统复杂性的有效方法,通过将原系统的状态空间进行扩展,得到各个子系统近似解耦的更为广大的扩展空间。在扩展空间中,不仅可以分析各个子系统之间的内在关系,还可以分别对各个子系统进行独立的动态控制器和观测器设计。之后,对分别设计的控制器和观测器进行合理有效地补偿,在满足包含原理收缩条件下,将其收缩回原系统空间中,对整体系统进行控制。由此可见,该方法既简化了复杂系统的分析与设计,又提高了系统的鲁棒性。有关系统包含原理的详细内容请参见文献[14]。
在具有信息结构约束下的系统中,每一个子系统可能与一个或多个子系统互联构成多种拓扑结构。其中最典型的是链型、环型和星型结构[7, 8]。本文所研究的群体机器人信息交换拓扑结构正是文献[8]中提到的星型结构。因此,本文以满足包含条件的典型约束a为例,应用星型结构系统的重叠结构分解方法,对模型如式(8)进行子系统对对分解,形成由2个子系统组成的有序排列基本互联子系统对R1-R2,R1-R3,R1-R4,R1-R5,R1-R6,R1-R7,如图 2(b)所示。首先根据文献[8]并考虑机器人R1为星型结构核心,选取如下扩展变换矩阵:

在扩展后的系统中,为了使机器人R1与其他6个机器人构成有序的子系统对,取系统的对称置换矩阵:
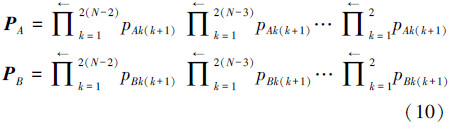
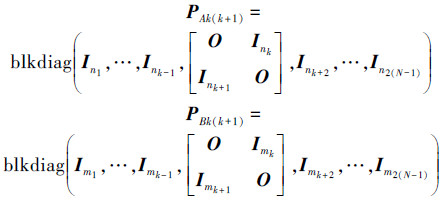
 表示矩阵的右向累乘。
表示矩阵的右向累乘。
经过对称置换后,扩展系统的状态矩阵和输入矩阵分别为
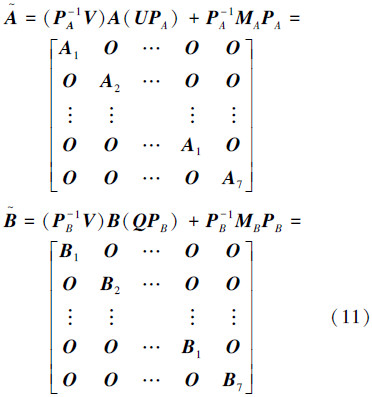

为了使上述提到的7个机器人从各自的初始状态到达指定的目标点并形成指定队形和速度方向的一致,参考文献[6]提出的广义一致性算法,针对Leader-follower系统对每个机器人子系统对设计如下控制规则:
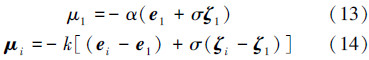
式(13)是领航机器人R1的控制输入,用于使机器人向目标点趋近,式(14)是跟随机器人的控制输入,用于在运动过程中保持与领航机器人之间的期望距离不变和速度一致。这充分体现了每个子系统对的一致协调控制,控制规则中有关参数的详细内容请参见文献[5, 6]。此外,还可以发现本文所研究的机器人子系统对的互联作用主要体现在跟随机器人的控制输入上,而并没有在系统状态空间中体现。根据式(13)、(14)得出子系统对的状态反馈增益矩阵:
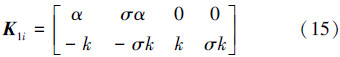
考虑到现实系统中存在的随机噪声,则每个子系统对的输入噪声和输出测量噪声的协方差序列分别表示为
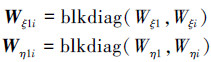
那么由子系统对的状态反馈增益矩阵K1i 所组成的扩展系统状态反馈增益矩阵,及由子系统对的观测增益矩阵L1i 所组成的扩展系统观测增益矩阵分别表示为

为了使分散控制器和观测器能反映重叠分散子系统对的互联关系,分散控制器和观测器与闭环系统应保持相同的信息结构约束,即分散控制增益矩阵和观测增益矩阵应与系统状态矩阵具有相同的结构[15]。由于本文的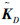 和
和 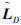 与
与 结构相同,因此不需要对其进行结构调整。
结构相同,因此不需要对其进行结构调整。
最后,采用满足包含条件约束a,将扩展系统的状态反馈增益矩阵收缩回原系统空间中,即
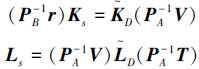
本文利用计算机仿真对结果作一个直观的分析。控制规则中的参数分别取α=2、σ=1和k=10,所有7个机器人的初始位置在[10:25; 0:15]范围内随机选取,同时初始速度的方向也随机选取,速率不超过10 m/s,设每个机器人的输入噪声和输出测量噪声向量序列分别为Wξi=0.05diag(1,1)和Wηi= 0.05diag(1,1,1,1),并保持图 1(a)所示的拓扑结构,如图 3所示。图 4是机器人在5 s仿真时间内形成正六边形队形,并使速度趋于一致的运动轨迹。其中目标队形用星号表示,领航者R1位于队形中心。从图中可以看出7个机器人在各自的初始状态下最终跟随领航者到达了指定的目标点,并形成了指定的正六边形队形,同时速度方向趋于一致。
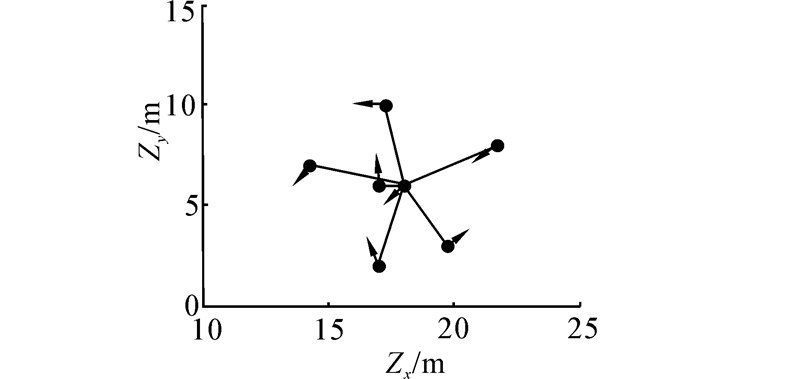 |
| 图 3 机器人初始状态 Fig. 3 Initial state of robots |
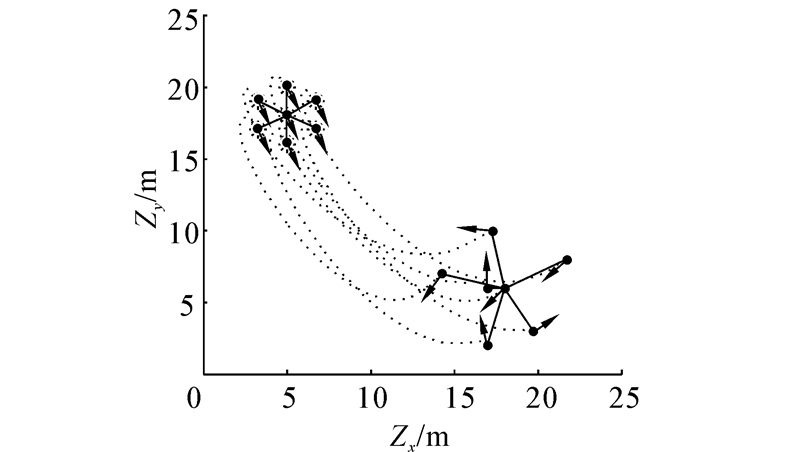 |
| 图 4 机器人运动轨迹 Fig. 4 Movement trajectory of robots |
图 5为各机器人与各自相应的目标点在x、y方向距离和x、y方向速度的仿真曲线,可以看出曲线渐进收敛并趋于一致。由此可以证明,基于系统包含原理的对对分解与分散协调控制方法在群体机器人系统队形形成与一致性上,特别是正六边形结构队形具有显著效果。
 |
| 图 5 原始图像和退化仿真图像 Fig. 5 Original image and simulated degraded image |
本文将包含原理的重叠互联系统对对分解与分散协调控制方法应用在了群体机器人的对形形成与一致性中。通过此方法,将群体机器人系统重叠展开,分解成多个有序的子系统对。根据广义一致性算法,并结合Leader-follower法的思想为每个子系统对设计相应的一致协调控制器。最后将扩展系统的控制器与观测器收缩回原系统,实现了群体机器人队形的形成与一致性。同时还考虑了现实系统中存在的噪声干扰,具有一定的理论意义与实际意义。此外,本文主要研究的是正六边形结构队形的形成,为今后群体机器人集结行为的研究起到了一定的作用。
| [1] | DAS A, FIERRO R, KUMAR V, et al. A vision based formation control framework[J]. IEEE Trans Robot Automat, 2001, 18: 813-825. |
| [2] | DEFOORT M, FBQUET T, KOKOSY A, et al. Sliding mode formation control for cooperative autonomous mobile robots[J]. IEEE Trans Iad Electron, 2008, 55: 3944-3953. |
| [3] | OGREN P, FIORELLI E, LEONARD N E. Cooperative control of mobile sensor network: adaptive gradient climbing in a distributed environment[J]. IEEE Trans Automat Contr, 2004, 49: 1292-1302. |
| [4] | MARSHALL J A, FUNG T, BROUCKE M E, et al. Experiment in multi-robot coordination[J]. Robotics and Autonomous, Systems, 2006, 54: 265-275. |
| [5] | REN W, ATKINS E M. Distributed multi-vehicle coordinated control via local information exchange[J]. Int J Robust Nonlinear Contr, 2007, 17: 1002-1033. |
| [6] | REN W, SORENSEN N. Distributed coordination architecture for multi-robot formation control[J]. Robotics and Autonomous, Systems, 2008, 56: 324-333. |
| [7] | CHEN X B, STANKOVIC S S. Decomposition and decentralized control of systems with multi-overlapping structure[J]. Automaton, 2005, 41: 1765-1772. |
| [8] | CHEN X B, STANKOVIC S S. Overlapping decentralized approach to automatic generation control of multi-area power systems[J]. International Journal of Control, 2007, 80: 386-402. |
| [9] | STANKOVIC S S, STANOJEVIC M J, SILJAK D D. Decentralized overlapping control of a platoon of vehicles[J]. IEEE Transactions on Control Systems Technology, 2000, 8: 816-832. |
| [10] | PALACIOS Q F, ROSELL J M, KARIMI H R. Semi-decentralized strategies in structural vibration control[J]. Modeling, Identification and control, 2011, 32: 57-77. |
| [11] | STIPANOVIC D M, INALHAN G, TEO R, et al. Decentralized overlapping control of unmanned aerial vehicles[J]. Automatica, 2004, 40: 1285-1296. |
| [12] | HASSAN K K. Nonlinear systems[M]. Beijing: Publishing House of Electronics Industry, 2005. |
| [13] | OLFATIC-SABER R. Flocking for multi-agent dynamic systems: algorithms and theory[J]. IEEE Transations on Automatic Control, 2006, 51: 401-420. |
| [14] | 陈雪波,系统包含原理及其应用[M]. 北京: 科学出版社, 2012. |
| [15] | CHEN X B, XU W B, HUANG T Y, et al. Pair-wise decomposition and coordinated control of complex systems[J]. Information Science, 2012, 185: 78-99. |



