2. 淮海工学院 计算机工程学院, 江苏 连云港 222005
2. Department of Computer Science, Huaihai Institute of Technology, Lianyungang 222005, China
社交网络服务是 Web 2.0 应用中的重要一类。这种系统帮助用户在互联网上与现实中的好友保持联络、分享内容等。然而随着社交网络的使用人数增加,用户分享的数据也不断上升,信息过载的问题也随之出现。另外,社交网络第1次提供了丰富的真实世界中人们的社交信息,利用这些信息的研究在各个学科中也不断出现。对于推荐系统来说,如何利用社交网络所提供的这些信息,进行更精确地推荐,成为一个重要研究方向[1, 2]。大部分推荐系统都采用协同过滤技术,它通过分析用户对相似项目以往的评分记录或相似用户对项目的评分模式来预测用户对某未知项目的评分。虽然协同过滤技术已成为解决推荐问题的标准方法,但传统的推荐系统只利用相关用户或相关商品的评分数据进行推荐,而并未考虑任何其他的信息。但当分析的信息量不断增大时,传统的推荐算法就会遇到诸多挑战,如数据稀疏问题、低质量的推荐以及信息源的不均衡性。
推荐系统通过识别和预测用户偏好,提供个性化服务,是缓解“信息过载”问题的重要手段之一。上下文感知计算是指系统能发现并有效利用上下文信息进行计算的一种计算模式,已经广泛应用于许多领域[3, 4]。上下文感知推荐系统通过将上下文信息引入推荐系统,成为一个刚刚兴起的领域,还有许多问题等待解决,如上下文用户偏好提取、高维数据稀疏性问题等[5]。
本文提出了一个新颖的融入上下文信息与社会网络信息的推荐系统——CS推荐算法,该系统首先抽取出与用户兴趣相关的上下文信息,然后应用随机决策树算法分解用户—项目评分矩阵,最终生成的用户—项目评分子矩阵(即决策树的叶子节点)包含了相似的评分。在产生的子矩阵中应用了矩阵因式分解技术进行用户对某一缺失项的评分预测。基于矩阵因式分解模型,本文还引进社会规范术语来改善推荐系统质量。为了衡量用户之间的相似程序,本文使用了上下文相关的皮尔逊相关系数来计算用户相似度。最后通过在2个真实的数据集上验证CS推荐系统的有效性。
1 相关工作目前,社会化推荐算法大都集中在如何利用用户间的社会关系来提高推荐的准确率。Yang等在文献[6]中认为用户间的信任关系强度并不是唯一的,而是受到其所处的朋友圈的影响,在不同的朋友圈中,用户间的信任关系也是不同的。他们通过给用户的朋友赋予不同的权重来对用户间的信任关系进行建模,并提出了一种基于朋友圈的社会化推荐算法。Noel等[7]针对社会化推荐算法在计算用户相似性时没有考虑到用户本身的特征、不能直接对用户间信息传播建模,不能反映用户间只有部分兴趣相同的问题,给出了一种将多种目标函数融合在一起的方法,并在矩阵分解的框架下进行求解。
然而,目前大部分社会网络推荐模型在度量2个用户的相似性时,基本都忽视了上下文信息。比如,即使一个用户和其朋友的品味极其相似,她对一部电影的评价可能还受其他因素影响(比如,她在看电影时候的情绪和陪她看电影的人)。因此近期的研究开始关注社交网络中的上下文信息。文献[8]提出了将用户和项目进行群组的方法,在协同过滤算法中利用了这些子群信息(一种上下文信息)来提高用推荐系统的质量。Liu等[9]利用推荐对象的属性上下文信息来对它们之间的关联关系进行度量,并通过估计出的关联关系信息来改善推荐的效果。文献[10]提出了将社会网络上下文信息(个人表现和交际影响)整合到一个矩阵分解模型中。但是,这样的上下文信息仅仅与社交关系有关,大量的非社交的上下文信息却被忽视了。相反,本文提出的CS算法运用机器学习技术和矩阵分解技术,不仅包含了大量的上下文信息,而且对上下文信息没有限定信息类型:上下文信息被显式地应用到矩阵划分中。基于信任度的皮尔逊相关系数提高了计算用户相似度的准确性。
2 CS推荐系统 2.1 预备知识 2.1.1 相关概念传统的推荐系统通常只考虑用户—项目评分矩阵来进行推荐。然而,在许多系统中,可以通过丰富的上下文信息来为推荐系统提供新的信息维度。本文把上下文信息分为2类:1)静态上下文,它描述用户的特性,例如年龄、性别、会员身份、角色等,或者是一种商品、种类、价钱、物理特性等;2)动态上下文,是一种与等级相关的即时信息(例如当一个用户评价一个产品时,他的心情和位置信息)。另一方面,在线社交网络也带来一些其他资源,通过分析这些资源一个用户的喜好可以由与他有相同品味的朋友推断出。因此,本文试图系统地融合上下文信息和社交网络信息来改善推荐性能。
用u={U1,U2,…,Um}表示用户集合,v={V1,V2,…,Vn}表示项目集合。所有用户可以根据自己的喜好为项目评分。假设分值为离散变量,范围为L={L1,L2,…,Lm}。比如,许多推荐系统(如MovieLens)使用五分制进行评分(例如[1,2,3,4,5])。用户Uu对项目Vv的评分表示为Ru,v,所有的评分集合R={Ru,v丨Uu∈u,Vv ∈v}构成一个用户—项目评分矩阵(如图 1(a))。正如上面提到的,假设对用户的每一个评分级Ri都存在与其相关的上下文信息集合,用Ci={c1,c2,…}来表示。对每种类型的上下文信息的值域没有限制,也就是说,离散值和连续值都是合法的。
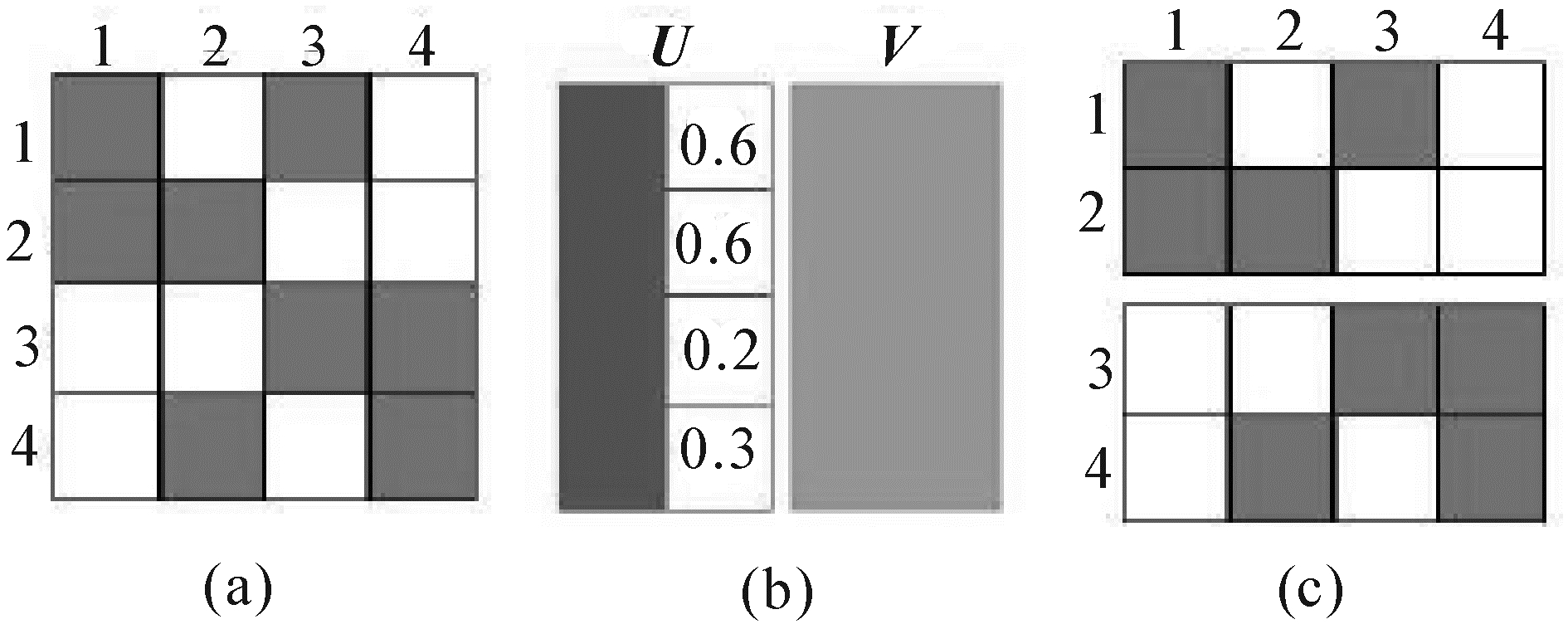 |
| 图 1 用户—项目评分矩阵分割过程Fig. 1 Illustration for division |
在社会网络中将用户信息及用户之间的关系可以抽象表示为有向带权值的社会网络图的形式: G=(V,E,C)。其中,V表示节点集合,每个节点代表网络中的用户个体; E表示边的集合,表示2个个体之间存在的关系;C={cuv}表示边的权重值,此值越大表示信任程度越大,本文将其定义为用户间的信任度。由于信任关系不是对称的,所以图中的边是有向的,网络图为有向图。
2.1.2 矩阵因式分解矩阵因式分解的目的是将一个矩阵分解成2个以上的矩阵,使得将矩阵因子相乘后可以重构或者近似原始矩阵。在推荐问题中,一个矩阵因式分解模型是将用户—项目评分矩阵 R ,R ∈ R m×n(m是用户数量,n是项目数量)分解成一个用户特征矩阵 U ,U ∈ R m×l和一个项目特征矩阵 V , V ∈ R l×n。

为了计算R,考虑到用户—项目评分矩阵的稀疏性,定义了以下的目标函数,即使预测评分与用户实际评分的误差最小化:
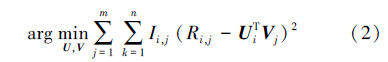
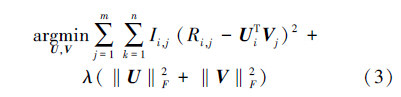
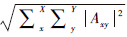 计算得到。参数λ控制规范化的范围。
计算得到。参数λ控制规范化的范围。
式3可以通过2种方式解得:1)随机梯度算法(SGD),通过迭代更新潜在用户特征因子和潜在项目特征因子;2)交替最小二乘算法(ALS),通过修正矩阵U (或者V )以优化V (或者U ),并且轮转迭代。
2.2 上下文感知的推荐模型本节首先介绍一下如何结合上下文信息来提高推荐系统的推荐准确度,在此暂不考虑社会关系。为了有效结合不同的上下文信息,使用一种具有较高学习精度的随机决策树算法。该算法的目标是对原始即用户—项目评分矩阵R使用随机划分策略将相似用户或相似项目的评分划分到树的同一结点中,即将具有相似上下文的评分划分在一个组内。由于是在相似的上下文中产生,因此在相同组里的评分将会比在原始评分矩阵中的评分具有更高的相关性,有助于提高推测缺失值的准确性。
对每个决策树中的每一个结点,利用式(2)对评分矩阵R进行基本的矩阵因式分解。经过分解之后,分别得到用户潜在特征向量与项目潜在特征向量(如图 1(b))。用户特征因子表明了用户在一些潜在主题上的兴趣分布,而项目特征因子代表了与这些主题相关的项目成员。为了划分评分矩阵R,选择了一个潜在特征(如图 1(b) U的第2列)和随机选取了一个分割值(本例中假设选择的分割值为0.4)。设定之后,则当前的评分矩阵被划分为2部分,如图 1(c)所示。在本例中,根据U中第2个潜在特征向量和随机选定的分割值,评分矩阵被从第2行和第3行之间分割成了2部分。由于第1个和第2个用户的潜在特征值比较相似,因此他们给出的评分被决策树划分到同一个结点中。
在为每个上下文信息构建决策树时,在树的每一层,算法都会从上下文信息集合C中随机选择一个上下文信息cr来划分评分矩阵(见图 2)。具体来说,评分矩阵是根据cr的值进行划分的。例如,如果假设上下文信息cr是一周时间,则评分矩阵可以根据每一天(即从周一到周六,工作日或者周末)来进行有意义的划分。另一方面,如果cr的值没有任何语义信息,则首先要对每一个评分cr进行标准化到某一特定区间(如[0, 1]),然后选择一个随机的阈值(如∈[0, 1])来划分评分。一旦在树中的某一层上完成了评分划分,则随机选取的上下文信息cr就会从上下文信息集合中被删除:C=C/cr,从而保证了一个上下文信息在一条路径上只被操作一次。
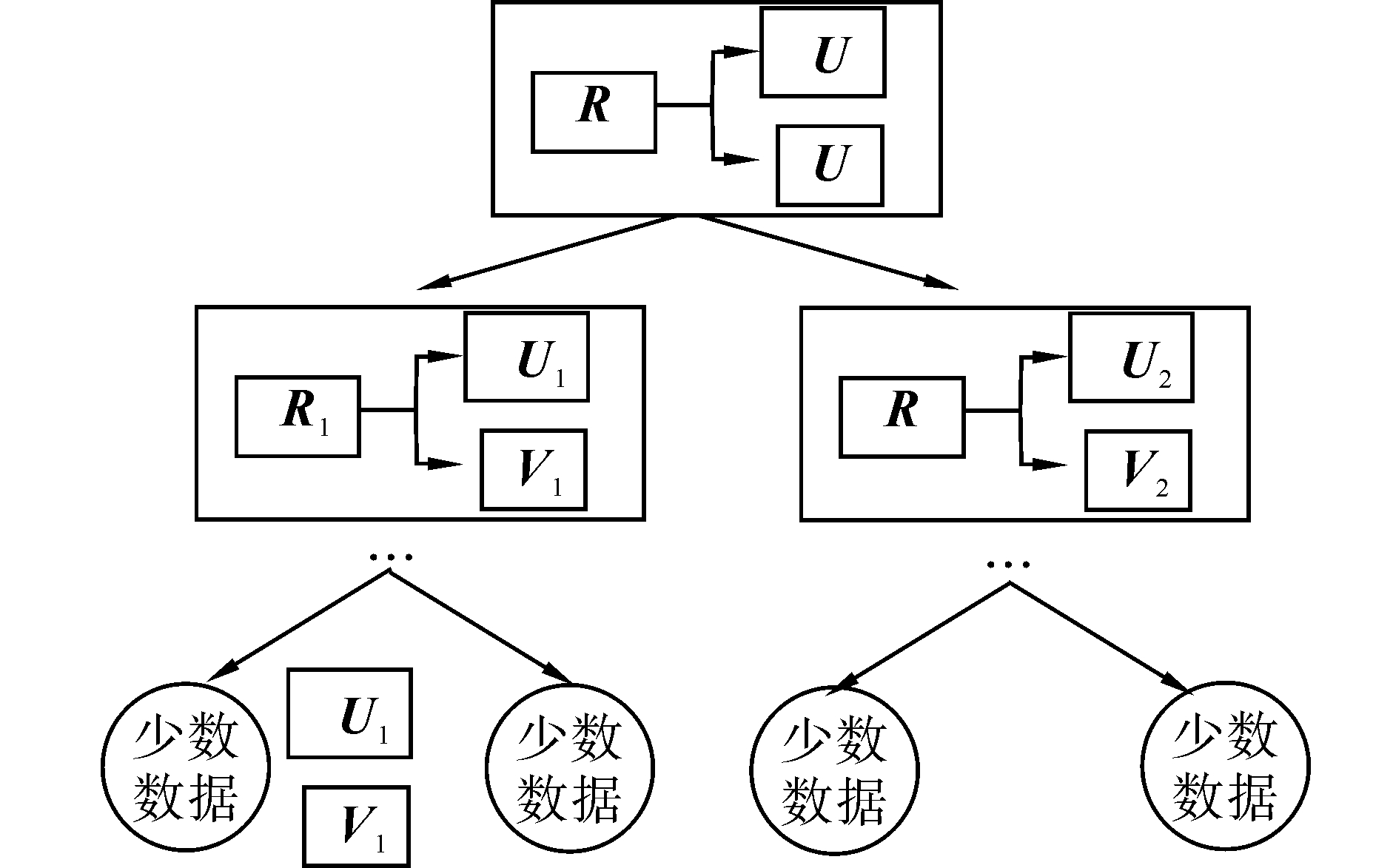 |
| 图 2 随机决策树划分过程Fig. 2 Main partition flow of random decision tree |
树的划分过程将一直继续,直到满足下列要求之一:1)所有的上下文信息都已经处理完毕; 2)决策树的深度达到了预定阈值。划分结束之后,评分矩阵R被不同的上下文信息分类到不同类别中(即图 2中树的叶子节点)。当预测一个缺失评分R m,在每个决策树中,根据R m的上下文信息对决策树进行划分,将其分类到用户—项目评分子矩阵Ri s⊂R 中。对于每一个R is,将其分解后分别得到用户特征因子U is和项目特征因子V is,它们能够被用来预测缺失评分R m(见式(4)、(5))。
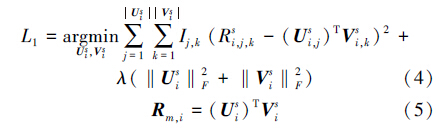
最终,将所有决策树得到的预测组合起来就可以得到对R m的最终预测得分
。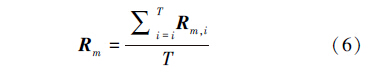
在2.2节提出的上下文感知推荐模型的基础上,本节将社交网络信息加入到推荐中以改善推荐质量。这种模型的假设前提与现实非常相符:在现实生活中,当用户在决定是否购买一个产品时往往会参考与自己有相似品味与兴趣的朋友所给出的建议。通过结合多个朋友的意见,用户最终会做出明智的选择。
尽管朋友能够提供有用的信息来帮助推荐系统为用户做出高质量的推荐,但现有的研究大部分都是在利用社会网络中所有的可用信息进行推荐,没有对这些信息进行细致地过滤;或者并没有深入地调查怎样精确计算用户之间的品味相似性。为了解决这些问题,本文引进一个新的社会规范化系数来对用户和他朋友之间的品味差异进行约束。在真实生活中,一个用户可能会有成百上千个朋友,因此同等对待朋友(或者朋友所给出的推荐信息)是没有意义的,因为其中的一些朋友可能与用户具有非常相似的品味,而与另一些朋友可能拥有完全不同的品味。为了解决这种社会网络中品味差异性问题,本文引入了社会规范化系数,在推荐系统中考虑了用户与其朋友之间的品味相似性:
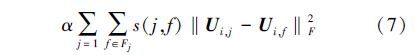
从式(7)中可以看出,融合社交网络信息的有效方法是通过研究用户与朋友之间的相似性来精确衡量每个朋友的观点,这种相似性可以通过他们以往的评分模式来推测,比如可以从他们共同评价过的商品的特性进行推测。现有许多相似性计算方法,其中皮尔逊相关系数已被证明比其他方法(如向量空间相似性)具有更高的精确性。因此本文也使用皮尔逊相关系数来衡量uj与其朋友uf的相似性。

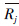 和
和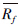 分别是uj和uf的平均评分。
分别是uj和uf的平均评分。
在社会网络中,每一个用户u都会有邻居集合Nu,用tuv表示节点u对节点v的社会信任度,其取值范围在[0, 1]。 值为0表示完成不信任,值为1表示完成信任。在社会网络中,tuv的值可以解释为用户u对用户v的了解与信任程度。但由于该权值包含一些噪音数据,不能体现社会网络中的整体结构信息,这就类似于在网页分析中的忽略了网页的链接结构信息。但其实在一个信任网络中,如果某个用户u信任大部分的用户,则其信任度应当被降低;反之,如果某个用户v被大部分用户所信任,则其信任度应该被增强。因此,综合考虑了社会网络的整体结构信息,利用式(9)对信任度进行了修正,修正后的信任度记为tuv*:
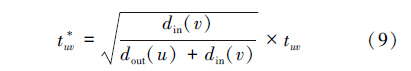
经典的相似性计算方法仅仅利用了评分的值,并未考虑用户之间的信任关系。为了进一步改善相似性计算的精确度,本文使用一种基于信任度的皮尔逊相关系数来计算用户之间的相似度:
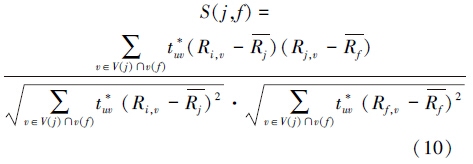
很明显,权重tuv*较大意味着用户之间的信任度越大,因此对整体的相似度计算时将会产生非常大的影响。应用式(7)和式(10),将式(4)重新定义为
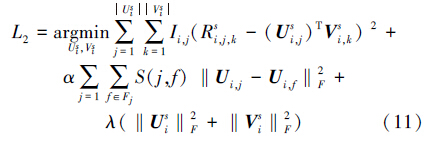
式(11)可以通过对Ui,j s和U i,ks应用梯度下降算法进行求解,这是一个不断迭代更新的过程。
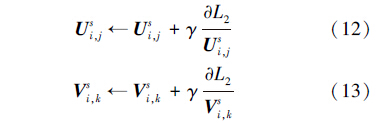
豆瓣网(www.douban.com)是中国最大的社交平台之一,许多人在这里分享对书、电影、音乐的评价。每个用户可以对书、电影、音乐进行评级(从一星到五星),表达他们对这些产品的喜好。在社交网络中如果某用户的评论被认为是有趣且有用的,则他就可能被其他用户所跟随。表 1列出了数据集的统计数据。
| 类别 | 评分数 | 用户数 | 项目数 |
| 书 | 812 037 | 8 598 | 169 982 |
| 电影 | 1 336 484 | 5 227 | 48 381 |
| 音乐 | 1 387 216 | 23 822 | 185 574 |
| 所有 | 3 535 737 | 25 560 | 403 937 |
选择豆瓣的数据因为它不仅包含了相关的时间/数据和其他可推断的上下文信息,而且还包含了社会网络信息,因此非常适合用于评估应用了多种类型信息的CS算法的性能。从豆瓣数据集中,随机选择80%的评价来训练推荐模型,使用剩下的20%比较它们的性能。
3.1.2 比较对象本文将CS推荐系统和目前主流的几种推荐方法进行了对比实验:传统的基于上下文感知推荐系统RPMF [14]、基于社会网络的推荐系统SoReg[11]、应用基本的矩阵分解模型构建的推荐系统BMF[12]。
与所有的上下文推荐系统相似,从数据集中可获得的上下文化信息中选取了5种类型的上下文信息:1)小时信息,即用户给出评分的时刻;2)日期信息,即用户给出评分的日期;3)当一个评价被给出的时候,对目标商品产生“期待”的数量;4)当目标用户评价一个特定商品时,其所给出评分的平均值;5)目标商品所属的类别。
3.1.3 度量标准实验选取在推荐系统评价中经常使用的2个度量标准来比较不同推荐模型的性能:平均绝对误差(MAE)和均方根误差(RMSE)。式(14)和(15)分别给出两者的定义:
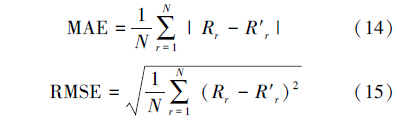
首先使用豆瓣网数据集来说明CS算法中不同参数值的选取对推荐性能的影响。经过交叉验证之后得到规则化常量λ=0.1。图 3给出了当数据集的不同子集(如书数据、电影数据、音乐数据)被应用时,CS推荐模型的性能如何随着参数值α的变化而变化,参数α决定了有多少社会网络信息量被整合进CS推荐模型中(见式11)。实验中设置在求解矩阵因式分解模型中潜在特征向量的维数为10,迭代求解次数为20。后续实验会给出这些变量的变化如何影响基于矩阵因式分解的推荐模型的性能。从图 3可以看出随着α值的增大,MAE和RMSE的值首先减少,接下来当到达一定阈值时(大约在α=0.1处)其值变得相对稳定(只是轻微下降)。因此可能得出社交网络信息可以有效改善推荐质量的结论,并且α=0.001是一个合适的阈值来很好地平衡用户—项目评分矩阵和社交网络信息。
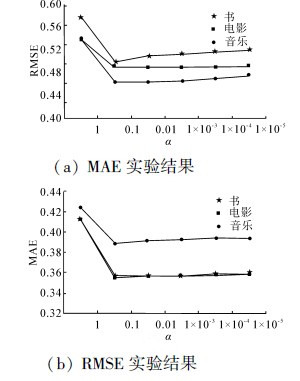 |
| 图 3 参数α的影响(λ=0.1,维数=10,迭代次数=20)Fig. 3 Impact of α(λ=0.1, dimensionality=10,iteration=20) |
接下来,验证上下文信息数量对推荐性能的影响。这一点可以通过控制决策树的高度来实现。也就是说,如果设树的高度为1,则只有一种类型的上下文信息在树的划分时被使用;如果设树的高度为4,表示所有的上下文信息都被应用到推荐系统中来。图 4给出了不同数量上下文信息的实验结果。
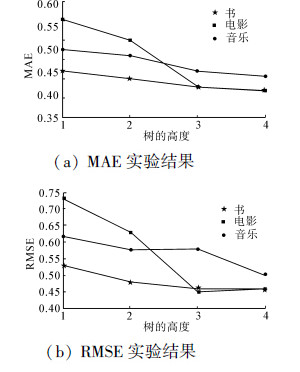 |
| 图 4 上下文信息数量的影响(λ=0.1,维数=10,迭代次数=20)Fig. 4 Impact of number of contextual information(λ=0.1,dimensionality=10,iteration=20) |
从图 4中可以看出在所有情况下,上下文信息越多则会产生越高的推荐精度,即MAE和RMSE的值越小。实验结果表明上下文信息很大程度上改善了推荐系统的性能,另一方面,从实验结果中可以看出本文所选取的上下文信息是非常有用的。
最后,将CS推荐系统和其他推荐系统的性能在豆瓣网数据集上做对比实验。在做对比实验之前,需要决定2个重要的参数的取值,即潜在特征向量的维度和基于矩阵因式分解模型的迭代次数。首先固定迭代次数为10,观察潜在特征向量在不同维度下的MAE取值,如表 1所示。发现随着维度的增加MAE的值在减少,这意味着随着维度的增加将会产生更高的推荐。但是当维度增加到大约10时,推荐质量的改进甚小。因此在实验中,为推荐算法的潜在特征向量维度设置为10。同理,本文为所有基于矩阵因式分解模型的迭代次数设置为20,因为更多的迭代次数并没有降低MAE 的值,反而会产生更高的开销。
参数一量确定,下面就分别使用书数据、电影数据、音乐数据和整个豆瓣网数据来比较不同推荐模型的推荐性能。表 2给出了对比结果。从图 5可以看出,本文提出的CS推荐模型所有的实验数据中都比其他推荐模型更加精确。所有基于矩阵因式分解的推荐模型都明显优于传统的基于项目和基于用户的协同过滤算法,这表明了矩阵因式分解技术在推荐领域的优势。实验结果也表明综合考虑上下文信息和社会网络信息比只考虑某一种信息类型的推荐模型(如SoReg 和RPMF)具有更高的推荐质量。
| 隐层 节点数 | 向量维度 | 迭代次数 | ||||||||||||
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 0 | 5 | 10 | 20 | 30 | 40 | 50 | |
| 书籍 | 0.4 | 0.38 | 0.37 | 0.38 | 0.37 | 0.37 | 0.37 | 0.5 | 0.4 | 0.36 | 0.35 | 0.35 | 0.36 | 0.36 |
| 电影 | 0.5 | 0.38 | 0.37 | 0.36 | 0.35 | 0.35 | 0.35 | 0.27 | 0.38 | 0.36 | 0.35 | 0.35 | 0.36 | 0.35 |
| 音乐 | 0.45 | 0.44 | 0.43 | 0.42 | 0.42 | 0.42 | 0.43 | 0.6 | 0.45 | 0.4 | 0.38 | 0.38 | 0.37 | 0.39 |
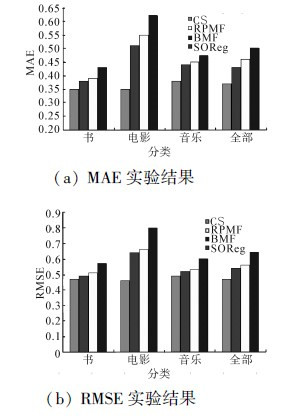 |
| 图 5 不同推荐模型的性能比较Fig. 5 Performance comparison for various model |
本文提出的CS算法是一个将上下文信息和社交网络信息相结合推荐算法,大大提高了推荐质量。该算法首先使用随机决策树算法基于不同的上下文信息对原始用户评分矩阵进行划分。划分后生成的子矩阵中包含相似上下文的评分,因此彼此间具有更大的影响。矩阵因式分解技术被应用到子矩阵中用来预测缺失评分。为了有效联合社会网络信息,CS算法引进额外的社会规则术语通过学习他朋友的品味来推断用户对一个项目的喜好。为了识别有相似品味的朋友,提出了一个基于上下文信息的皮尔逊系数来衡量用户与朋友的相似性。在2个真实数据集上进行的验证,实验结果表明CS推荐算法明显优于传统的基于上下文信息和基于社交网络的推荐模型。
| [1] | ZHAO Du, FU Xiaolong. Scalable and explainable friend recommendation in campus social network system[J]. Frontier and Future Development of Information Technology in Medicine and Education, 2014, 269(1): 457-466. |
| [2] | CHEN Cheng, MAO Chengjie, TANG Yong. Personalized recommendation based on implicit social network of researchers[J]. Pervasive Computing and the Networked World, 2013, 7719(10): 97-107. |
| [3] | ZHONG Erheng, FAN Wei, YANG Qiang. Contextual collaborative filtering via hierarchical matrix factorization[C]//Proceedings of the Siam Internatiohnal Conference on Data Mining. Texas, USA , 2012: 744-755. |
| [4] | RENDLE S, GANTNER Z, FREUDENTHALER C. Fast context-aware recommendations with factorization machines[C]//Proceedings of the 34th International ACM SIGIR Conference. Beijing, China, 2011: 230-241. |
| [5] | BALTRUNAS L, LUDWIG B, RICCI F. Matrix factorization techniques for context aware recommendation[C]//Proceedings of the Fifth ACM Conference on Recommender Systems. Chicago, USA, 2011: 301-304. |
| [6] | YANG Xiwang, STECK H, LIU Yong. Circle-based recommendation in online social networks[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Beijing, China, 2012: 1267-1275. |
| [7] | NOEL J, SANNER S, TRAN K. New objective functions for social collaborative filtering[C]//Proceedings of the 21th International Conference on World Wide Web Lyon, France, 2012: 859-868. |
| [8] | XU Bin, BU Jiajun, CHEN Chun. An exploration of improving collaborative recommender systems via user-item subgroups[C]//Proceedings of the 21st International Conference on World Wide Web. Lyon, France, 2012: 21-31. |
| [9] | LIU Qiang, WANG Chengwei, XU Congfu. A modified PMF model incorporating implicit item associations[C]//Proceedings of the International Conference on Tools with Artificial Intelligence. Athens, Greece, 2012: 7-9. |
| [10] | JIANG Ming, CUI Peng, LIU Rui. Social contextual recommendation[C]//Proceedings of the 21st ACM International Conference on Information and Knowledge Management. Maui, USA, 2012: 566-578. |
| [11] | MA Hao, ZHOU Dengyong, LIU Chao. Recommender systems with social regularization[C]//Proceedings of the Fourth ACM International Conference on Web Search And Data Mining. Hong Kong, China, 2011: 287-296. |
| [12] | MA Hao, YANG Haixuan, LYU M R. Sorec: social recommendation using probabilistic matrix factorization[C]//Proceedings of the 17th ACM Conference on Information and Knowledge Management. [S.l.], USA, 2008: 931-940. |



