模式匹配是许多领域的关键操作,是模式对象间的映射或相应关系的识别[1]。由于模式对象间的语义不能完全来源于数据和元数据信息,因此模式匹配中存在固有的不确定性,而且其不确定性会影响模式集成的整个过程[2],被认为是开展大规模数据集成的一个关键瓶颈,不确定性管理是未来的挑战之一[3]。通常,自动或是半自动模式匹配的方法都是耗时和难于实施的,尤其是进行大规模模式匹配就更困难了,但若能在具体模式匹配实施前,对整个过程进行不确定性度量,将会为模式匹配在语义Web、模式集成、无线网络和电子商务等诸多领域中的高效应用提供决策参考。
模式匹配实质上是一多属性决策过程[4],其过程中需要考虑一定的不确定性。对模式匹配不确定性的度量研究目前比较少,相关领域主要针对科学数据库和确定数据库进行基于确定语义的匹配操作,主要目的是尽量提高映射结果的正确率。不确定模式匹配的相关研究中,基于不确定语义映射的模式集成[2]、基于相似度计算的方法[5]、基于概率映射的模式匹配方法[6]、基于by-table和by-tuple的数据集成方法[7]和Top-K方法[8]等均是在匹配结果上尽量提高输出正确率,而抛弃掉一些不确定性信息和结果,因此会丢失一些对用户有用的信息,并且这些研究工作中均未对整个匹配的不确定性进行度量,未考虑匹配过程中不确定性因素对结果的综合影响。由B.Liu在2007年提出的不确定性度量适用于不精确数量数据的度量[9, 10]。与本文相近的工作有AMUR算法和粗糙集(rough set,RS)的不确定性度量,AMUR算法处理的对象是RFID数据[11]。RS理论是由波兰科学家Pawlak[12]在1982年提出的一种有效处理不确定性的工具,对RS不确定性度量的研究是近年来的研究热点,在经典RS理论中,产生不确定性的原因有集合的粗糙性和知识(概念)的不确定性[13]。基于信息熵的度量方法[14]能够反映出产生不确定性的2个因素,但不能够全面地反映出知识不确定性,该方法被应用在粗糙集的异常值发觉中;基于不确定熵的度量方法[13]综合了粗糙熵、精确度和包含度3种基本方法,能够反映出粗糙性和知识的不确定性;基于知识粒度的不确定性度量方法[15]适于解决集合的粗糙性;定位服务的不确定性度量方法[16]运用粗糙集和证据理论进行不确定性度量。这些方法的实际应用范围有限,容易受系统规模的影响,且未详细讨论不确定性因素对度量结果的影响程度。
本文针对不确定性模式匹配的处理过程[17],提出了一个多因素集结的模式匹配不确定性度量模型,根据语义匹配和属性匹配不确定性因素的特点,运用全知熵度量其中的不确定性,并引入过程不确定性度量方法对匹配决策的不确定性进行了度量。根据不确定性因素间的相互关系,给出了一个集结算子,用于判断各不确定性因素的影响程度和合成度量结果以生成总不确定率。所提出的模型和方法能够有效度量模式匹配的不确定性,能够综合各不确定性因素产生的影响,能够处理大规模模式匹配的不确定性度量,为复杂系统的不确定性度量奠定了基础。
1 模式匹配中的不确定性根据不确定性模式匹配的处理过程,模式匹配(schema matching,SM)的不确定性主要出现在语义匹配、属性匹配和匹配决策过程中,存在于其中的不确定性表现[17],可归结为语义因素、属性因素和过程决策因素,这3个不确定性因素具有源发性和主导性。
定义1 不确定语义匹配。2个模式S1和S2的不确定语义匹配是一个三元组〈S,O,UM〉,其中S是模式有限集,S1,S2∈S,O∈Si是模式对象有限集,UM = {〈r11,m11〉,〈 r12,m12〉,…,〈r1k,m1k〉,〈r21,m21〉,…,〈rnk,mnk 〉}是模式对象间的不确定匹配关系集,rij∈R,i=1,2,…,n,j=1,2,…,k,n=|S1|和k=|S2|为所包含模式对象的个数,R={相等,包含,相交,超集,不相交,不相容}是6种相互排斥的语义关系集,mij为rij的不确定率。
定义2 不确定属性匹配。2个模式对象的不确定属性匹配是一个三元组〈A,T,UD〉,其中A是属性集,T={ANM,ATM,KRM,DIM}是匹配类型集,ANM是属性名匹配,ATM是属性数据类型匹配,KRM是关键字约束匹配,DIM是数据实例匹配,UD={〈A1 ,UD 1〉,〈A2,UD2〉,〈A3 ,UD3〉,〈A4 ,UD4〉}是各类属性匹配的不确定率集,Ai∈A。
定义3 不确定决策过程。不确定决策过程UDP是一个四元组〈T,ST,P,f〉,其中T是任务集,ST是状态集,P是不确定度集,f:T×ST→P是一个决策函数。
定义4 模式匹配的不确定性度量。模式匹配的不确定性度量是满足系统不确定性度量[18]中4个条件的不确定性度量。
2 模式匹配的不确定性度量 2.1 不确定性度量模型模式集成中的模式匹配不确定性度量模型由模式对象清洗(schema object cleanout,SOC)、语义匹配不确定性度量(uncertainty measure of semantic matching,UMSM)、属性匹配不确定性度量(uncertainty measure of attribute matching,UMAM)、决策过程不确定性度量(uncertainty measure of process,UMP)和不确定性度量合成器(uncertainty measure synthesizer,UMS)5个模块组成。模式匹配不确定性度量模型的框架如图 1所示。
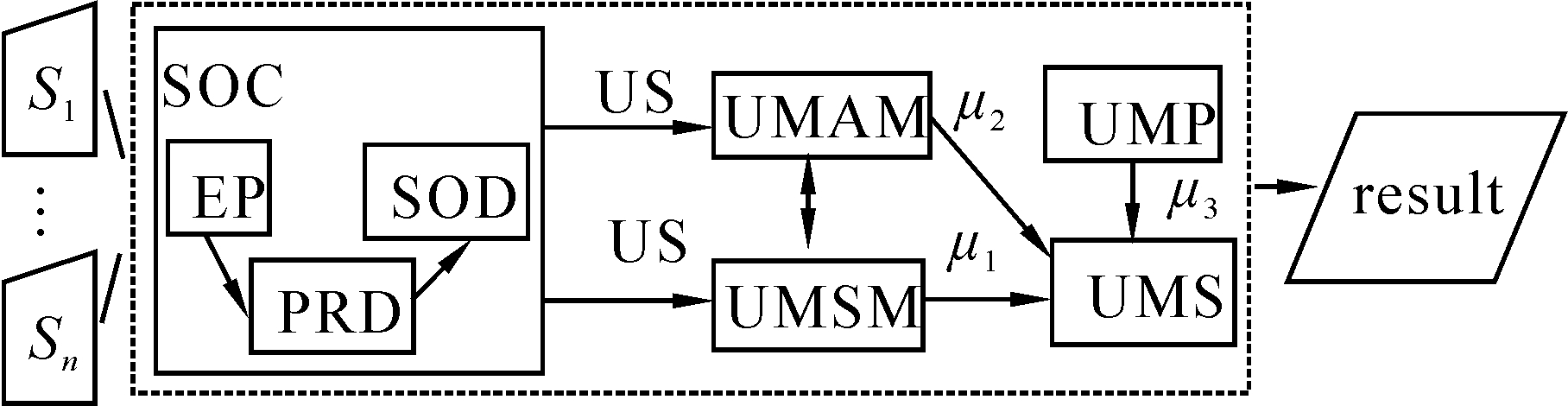 |
| 图 1 模式匹配不确定性的度量模型Fig. 1 Uncertainty measure model for schema matching |
模式匹配的复杂度会随数据集成规模的增大而增大,对输入模式进行预处理至关重要。在SOC中使用属性约减方法[19]对输入模式所包含的模式对象进行等价类划分(equipollence partition,EP)后,再进行正域约减(positive region deduction,PRD)和模式对象约简(schema object deduction,SOD),得到可能存在不确定性的部分——模式对象约简集。模式匹配不确定性的度量规模经过SOC的处理后明显缩小。
2.3 基于全知熵的不确定性度量粗糙性是指由于知识的不完备性或不精确性,导致对象与对象之间不可分辨,从而使得对象与概念之间的关系具有不确定性[12]。信息熵是信息理论中用于分析不确定程度的一种重要度量,以所需信息量的多少来衡量不确定性的程度[20]。基于信息熵的度量方式中全知熵不确定率对系统的不确定性比较敏感,能够较为准确地反映不确定性的变化规律[21]。模式匹配的执行过程能够表达其系统内的条件属性知识和决策属性知识,模式匹配的不确定性结构和程度可由属性知识完全确定,因此基于全知熵的度量方式适于度量模式匹配的不确定性。
2.3.1 模式匹配的全知熵不确定率定义5 模式匹配的全知熵不确定率。 四元组DS= (O,MA,V,f)为模式匹配决策系统,其中,O为模式对象有限集;MA=C∪D是匹配属性的集合,C为不确定匹配关系集,D为决策属性集,C∩D=Φ,a∈C∪D;V=∪Va是属性的值域,f:O×MA→V是一个信息函数。模式匹配的全知熵不确定率定义为
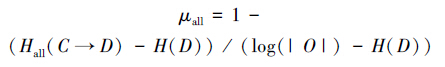
可将模式匹配看做一个决策系统,C的元素为定义1中R所包含的元素,D={0(不是),1(是),2(不确定)}。所定义的不确定率满足粗糙集不确定性度量的基本准则。
定理 模式匹配的全知熵不确定率满足粗糙集不确定性度量的基本准则。
证明 全知熵不确定率μall= 1- (Hall(C→D) - H(D)) / (log(|O|) - H(D))= 1-(H(C)+H(D|C)- H(D)) / (log(|O|) - H(D))。R1和R2是U上的2个等价关系。
1)0≤(H(C)+H(D|C)- H(D)) / (log(|O|) - H(D))≤1,因此0≤μall≤1非负;
2)若R1≈R2,则H(C1)= H(C2),H(D1)= H(D2),所以μall满足不变性;
3) 若R1<R2,则根据文献[22]的定理7有H(C1) <H(C2),H(D1)<H(D2),所以μall满足单调性。
综上所述,模式匹配的全知熵不确定率满足粗糙集不确定性度量的基本准则[23]。
2.3.2 语义匹配的不确定性度量语义匹配是用于确定各模式及其模式对象间匹配程度的过程之一,由于模式对象的语义不能完全来源于数据和元数据信息,并且识别确定的语义映射是非常困难的,因此语义匹配中产生的不确定性是模式匹配中存在不确定性的主因之一[24]。语义匹配是一决策过程,语义匹配的不确定率如下:
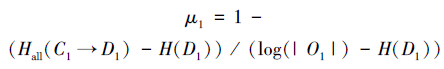
属性匹配不确定性的度量由UMAM来完成,实现属性名匹配(ANM)、数据类型匹配(ATM)、关键字约束匹配(KRM)和数据实例匹配(DIM)的不确定性度量,计算出属性匹配的总不确定率。属性匹配过程同样是一决策过程,其中的条件属性集合均为{相等,包含,相交,超集,不相交}。
根据定义5属性匹配的不确定率如下:
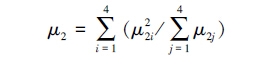
 ,j=1,2,3,4,是各属性匹配不确定率的权值。
2.4 匹配决策过程的不确定性度量
,j=1,2,3,4,是各属性匹配不确定率的权值。
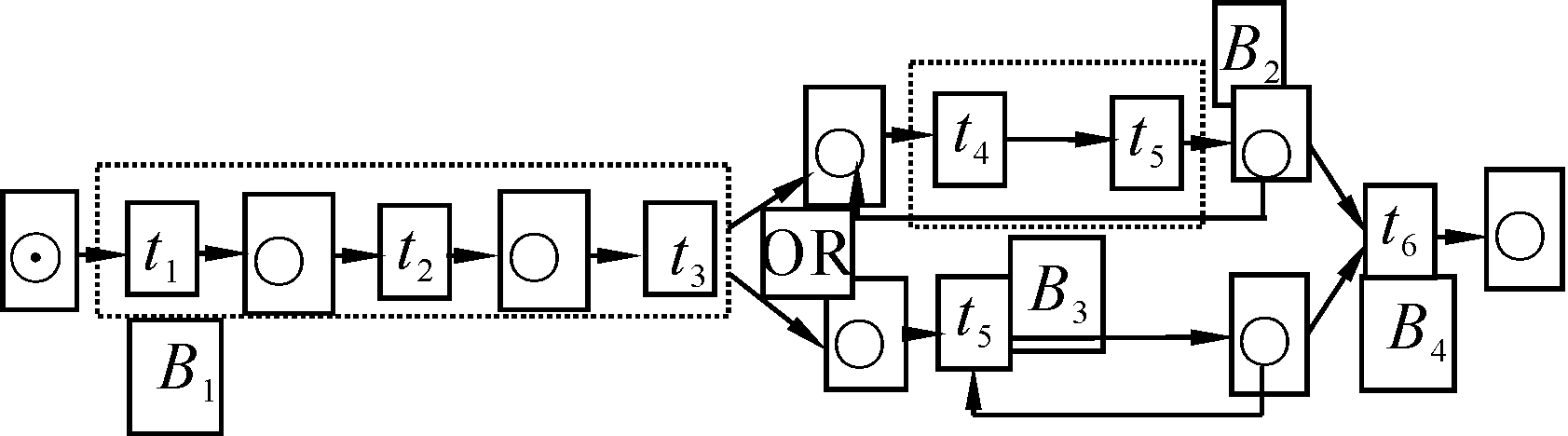
2.4 匹配决策过程的不确定性度量模式匹配是根据运行时管理者的决策或过程数据有条件执行的,因而其过程中存在不确定性是毫无疑问的[25]。用Petrinets表示模式匹配的决策过程(decision process,DP),如图 2。
 |
| 图 2 模式匹配的过程模型Fig. 2 Process model of schema matching |
ti为任务块,B1为SOC的执行过程,B2为语义匹配和属性匹配的顺序执行过程,B3为属性匹配的执行过程,B4为匹配结果合并过程。图 2可转换为图 3形式。
 |
| 图 3 转换后的过程模型Fig. 3 Converted process model |
决策过程不确定性的计算通式如下:

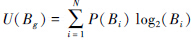 。
。
决策过程不确定率μ3的计算公式如下:

影响模式匹配的不确定因素之间往往不是孤立的,它们之间可能存在着某些关系,这将影响不确定性的准确度量,各因素及其权重的简单线性组合也从一定程度上忽略了这些因素之间存在的相互关系[26]。
定义6 不确定性的集结度量。U(SM)=f(S(SM),A(SM),P(SM)) 称为模式匹配SM不确定性的集结度量,U(SM) ∈[0, 1],U(SM)越大SM的不确定性就越大,其中f称为以S(SM)、 A(SM)和P(SM)为自变量的不确定性度量函数,f:[0, 1]×[0, 1]×[0, 1] →[0,1]。
基于f对SM不确定性的度量将所有不确定性因素映射到一个[0, 1]上,反映了模式匹配的不确定性。
模式匹配中任何不确定因素的细微变化都将影响到整个过程。综合语义匹配、属性匹配和决策过程这3个方面的不确定因素以进行模式匹配不确定性的客观度量,而不是各因素的简单线性组合,需要考虑这3个因素的内在关系。为了讨论单个因素对不确定性的影响以及多个因素集结起来对不确定性的影响,下面给出相关定义。
定义7 分别对因素S(SM),A(SM)和P(SM)作如下变换:

令因素e∈{S(SM),A(SM),P(SM)},相应地,z∈{S′(SM),A′(SM),P′(SM)}称为因素e对SM不确定性的影响,z∈[-1, 1]。若z≥0,则称e为积极因素;若z=0,则称e为不变因素;若z<0,则称e为消极因素。
定义8 若给定z1,z2∈{S′(SM),A′(SM),P′(SM)},z1≠z2,集结算子定义如下:
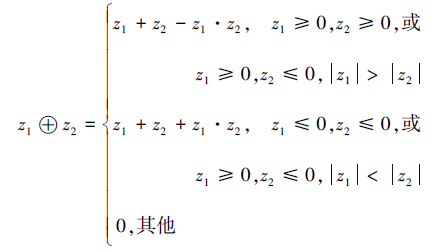
若已存在一个不确定因素e1,再给定一个不确定因素e2,它们的影响分别为z1和z2,则2个因素c之间的内在相互关系有如下特性:
1)增长性,若e2是一个积极因素,即z2>0。e1和e2对SM不确定性的集结影响z应该满足z> z1;若e1也是一个积极因素,则z>z2也同样成立。
2)不变性,若e2是一个不变因素,即z2=0。e1和e2对SM不确定性的集结影响z应该满足z=z1,即SM的不确定性受e1的影响大;若e1也是一个不变因素,则SM的不确定性不受加入因素的影响。
3)减弱性,若e2是一个消极因素,即z2<0。e1和e2对SM不确定性的集结影响z应该满足z<z1;若e1也是一个消极因素,则z<z2也同样成立。一个积极因素和一个消极因素对SM不确定性的集结影响取决于绝对值大的因素,且集结影响值小于较大的绝对值。
4)有界性,z1⊕z2∈[-1, 1],以确保多个因素的集结影响可以通过两两集结来实现。
5)交换率,z1⊕z2= z2⊕z1,这可以保证2个给定不确定性因素对SM不确定性的影响保持不变。
6)结合率,(z1⊕z2)⊕z3= z1⊕(z2⊕z3),这表明2个以上因素的集结影响与各因素参与计算的次序无关。
3.2 总不确定率模式匹配的总不确定率主要由3部分来确定,分别是语义匹配的不确定率S(M)、属性匹配的不确定率A(M)和决策过程的不确定率P(M)。由于z1⊕z2⊕z3∈[-1, 1],而模式匹配不确定性度量函数的值域为[0, 1],因此模式匹配不确定性的度量函数(即,总不确定率)定义为
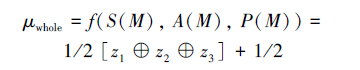
设计2种实验方案:1)较小不确定性的度量。对2个模式S1(在校生)和S2(毕业生)间的匹配进行不确定性度量,所包含模式对象的详细信息分别如图 4、5所示;2)多模式对象匹配不确定性的度量。对5个模式间的匹配进行不确定性度量,共包含57个模式对象,实验数据情况见表 1。实验参数见表 2。属性匹配包括属性名匹配(ANM)、属性类型匹配(ATM)、关键字匹配(KRM)和数据实例匹配(DIM)4个过程,每个过程中条件属性个数|C|=6,条件属性值域VC={0,1,2},每个过程中的模式个数和模式对象个数见表 3。模式匹配的不确定率见表 4。
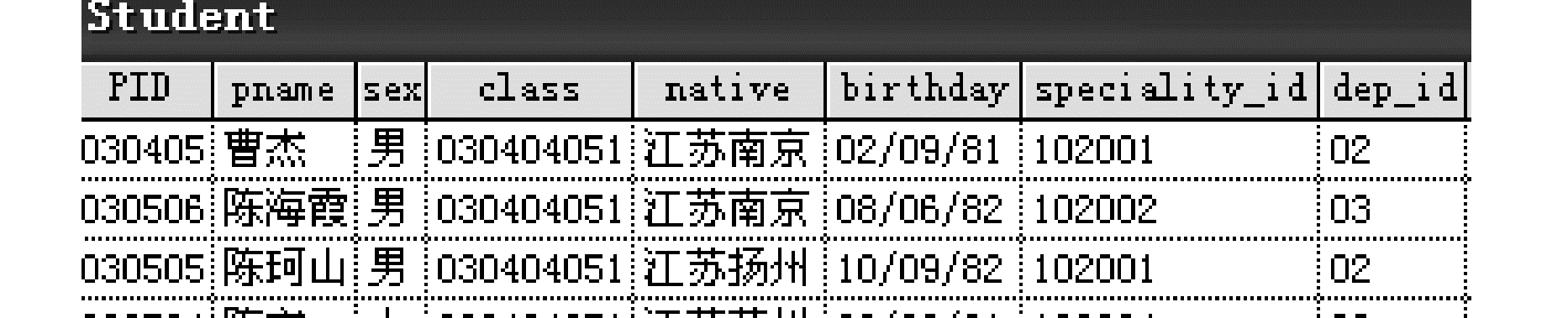 |
| 图 4 存储在校生数据的模式截图Fig. 4 Schema data of undergraduate |
 |
| 图 5 存储毕业生数据的模式截图Fig. 5 Schema data of graduate |
| 序号 | 年份 | 对象个数 |
| 1 | 2005sp | 17 |
| 2 | 2006au | 17 |
| 3 | 2007au | 7 |
| 4 | 2008sp | 9 |
| 5 | 2009sp | 7 |
| 注:表中数据为2005年春至2009年春江苏省VFP二级考试的数据情况 | ||
| No. | 模式 个数|S| | 模式对 象个数|U| | 条件属性 | 决策属性 | ||
| |C1| | VC1 | |D1| | VD1 | |||
| 1 | 2 | 2 | 6 | {0,1,2} | 1 | 0,1,2} |
| 2 | 5 | 52 | 6 | {0,1,2} | 1 | {0,1,2} |
| 注:{0,1,2}中,0—是,1—不是,2—不确定 | ||||||
| 匹配类型 | 方案1 | 方案2 | ||
| |S| | |U| | |S| | |U| | |
| ANM | 2 | 12 | 5 | 301 |
| ATM | 2 | 16 | 5 | 301 |
| KRM | 2 | 2 | 5 | 5 |
| DIM | 2 | 300 | 5 | 3501 |
| 第1种方案 | 第2种方案 | |
| USM | μ1=0 | μ1=0.34 |
| UAM | μ2=0.21 | μ2=0.95 |
| DP | μ3=0.17 | μ3=0.17 |
| 总计 | μwhole=0.19 | μwhole=0.72 |
第1种方案中,首先通过SOC处理后,匹配规模比[2]中降低50%。2个模式的模式对象名语义相同,因此μ1=0。属性匹配中只有属性名匹配具有不确定性。决策过程中的不确定率随模式匹配规模的减小而降低,利用公式计算得到的μwhole值符合实际情况。第2种方案中,模式对象规模和属性匹配的规模突然增大,通过SOC的处理后,匹配规模降低了近1/10,同时计算效率也明显提高,不确定率随匹配规模增大而增大符合不确定性度量的基本准则。实验表明度量模式匹配不确定性的模型和不确定率计算方法具有可行性、有效性、可扩展性和高效性。
5 结束语模式匹配的不确定性研究是国际上相关领域近年来才兴起的热点研究方向,度量原始匹配的不确定性是关键问题。本文根据模式匹配中产生不确定性的主要因素,首次将全知熵不确定率和过程不确定率结合起来,并证明模式匹配的全知熵不确定率满足粗糙集不确定性度量的基本准则,提出了一个多因素集结的模式匹配不确定性度量模型,利用集结算子判断各不确定性因素对模式匹配不确定性的影响程度和合成各阶段的度量结果,实验证明本文提出的方法与已有方法相比可获得更加合理的度量结果。所提模型解决了不确定性度量中规模限制问题,使得大规模模式匹配不确定性的处理复杂度降低。下一步的工作将探讨动态环境下模式匹配不确定性的度量方法及其处理过程中不确定性传播的测算方法。
| [1] | SHVAIKO P, EUZENAT J. A survey of schema-based matching approaches[J]. Journal on Data Semantics IV, 2005(3730): 146-171. |
| [2] | MAGNANI M, RIZOPOULOS N, BRIEN P, et al. Schema integration based on uncertain semantic mappings[J]. Lecture Notes in Computer Science, 2005(3716): 31-46. |
| [3] | HALEVY A, RAJARAMAN A, ORDILLE J. Data integration:the teenage years[Z]. Seoul, 2006: 9-16. |
| [4] | 翁年凤,刁兴春,曹建军,等. 不确定模式匹配研究综述[J]. 计算机科学, 2011, 38(12): 1-5.WENG Nianfeng, DIAO Xingchun, CHAO Jianjun, et al. Survey of uncertain schema matching[J]. Computer Science, 2011, 38(12): 1-5. |
| [5] | 姜芳艽,孟小峰,贾琳琳. Deep Web 集成服务的不确定模式匹配[J]. 计算机学报, 2008, 31(8): 1412-1421.JIANG Fangjiao, MENG Xiaofeng, JIA Linlin. Uncertain schema matching in deep web integration service[J]. Chinese Journal of Computers, 2008, 31(8): 1412-1421. |
| [6] | MAGNANI M, MONTESI D. Probabilistic data integration[R]. Bologna(italy): UBLCS, 2009. |
| [7] | DONG X L, HALEVY A, YU CONG. Data integration with uncertainty[J]. The VLDB Journal, 2009, 18: 469-500. |
| [8] | AVIGDOR G. Managing uncertainty in schema matching with top-k schema mappings[J]. Journal on Data Semantics, 2006, 6: 90-114. |
| [9] | LIU Baoding. Uncertainty theory[M]. Berlin: Springer-Verlag, 2007: 3-12. |
| [10] | LIU Baoding. Some research problems in uncertainty theory[J]. Journal of Uncertain Systems, 2009, 3(1): 3-10. |
| [11] | 王永利,钱江波,孙淑荣. AMUR:一种RFID数据不确定性的自适应度量算法[J]. 电子学报, 2011, 39(3): 579-584.WANG Yongli, QIAN Jiangbo, SUN Shurong. AMUR: an adaptive measuring algorithm of underlying uncertainty for rfid data[J]. Chinese of Journal Electronics, 2011, 39(3): 579-584. |
| [12] | PAWLAL Z. Rough sets[J]. International Journal of Computer and Information Science, 1982, 11(5): 341-356. |
| [13] | QIU Taorong, YOU Min, GE Hanjuan, et al. A method of uncertainty measure based on rough set[Z]. 2008: 544-547. |
| [14] | JIANG Feng, SUI Yuefei, CAO Cungen. An information entropy-based approach to outlier detection in rough sets[J]. Expert Systems with Applications, 2010, 37(9): 6338-6344. |
| [15] | LIANG Jiye, WANG Junhong, QIAN Yuhua. A new measure of uncertainty based on knowledge granulation for rough sets[J]. Information Sciences, 2009, 179(4): 458-470. |
| [16] | IFTIKHAR-U S, ARYYA G. Managing uncertainty in location services using rough set and evidence theory[J]. Expert System with Application, 2007, 32(2): 386-396. |
| [17] | 胡文彬,李千目,张宏. 基于领域知识的不确定性关系模式集成[J]. 南京理工大学学报:自然科学版, 2010, 34(4): 409-414.HU Wenbin, LI Qianmu, ZHANG Hong. Uncertain relation schema integration based on domain knowledge[J]. Journal of Nanjing University of Science and Technology: Natural Science, 2010, 34(4): 409-414. |
| [18] | 胡文彬,张宏,李千目. 基于全知熵的模式集成不确定性度量模型[J]. 南京航空航天大学学报, 2012, 44(4): 575-579.HU Wenbin, ZHANG Hong, LI Qianmu. Uncertainty measure model of schema integration based on all known entropy[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(4): 575-579. |
| [19] | WANG J G, MENG G Y, ZHENG X L. The attribute reduce based on rough sets and sat algorithm[Z]. 2008: 98-102. |
| [20] | LIANG Jiye, QIAN Yuhua. Information granules and entropy theory in information systems[J]. Science in China Series F: Information Sciences, 2008, 51(10): 1427-1444. |
| [21] | 赵军,周应华. 基于粗集理论的系统不确定性度量方式研究[J]. 小型微型计算机系统, 2010, 31(2): 354-359.ZHAO Jun, ZHOU Yinghua. Study on system uncertainty measures based on rough set theory[J]. Journalof Chinese Computer Systems, 2010, 31(2): 354-359. |
| [22] | YU Daren, HU Qinghua, WU Congxin. Uncertainty measures for fuzzy relations and their applications[J]. Applied Soft Computing, 2007, 7(3): 1135-1143. |
| [23] | 胡军,王国胤. 粗糙集的不确定性度量准则[J]. 模式识别与人工智能, 2010, 23(5): 606-615.HU Jun, WANG Guoyin. Uncertainty measure rule sets of rough sets[J]. Pattern Recognition and Artificial Intelligence. 2010, 23(5): 606-615. |
| [24] | MAGNANI M, MONTESI D. Uncertainty in data integration:current approaches and open problems[M]. Enschede, The Netherlands: the Centre for Telematics and Information Technology, 2007: 26-32. |
| [25] | JUNG J Y, CHIN C H, CARDOSO J. An entropy-based uncertainty measure of process models[J]. Information Processing Letters, 2011, 111(3): 135-141. |
| [26] | 岳昆,刘惟一,王晓玲. 一种基于不确定性因素叠加的Web服务质量度量方法[J]. 计算机研究与发展, 2009, 46(5): 841-849.YUE Kun, LIU Weiyi, WANG Xiaoling. An approach for measuring quality of web services based on the superposition of uncertain factors[J].Journal of Computer Research and Development, 2009, 46(5): 841-849. |



