科学合理地确定属性权重关系是多属性决策领域研究的核心问题,关系到决策结果的可靠性与正确性[1]。属性权重应能从宏观上体现决策目标,有效地反映各属性对目标的影响程度,体现决策者的评价目的和决策者对不同属性的重视程度,能较好地遵循重要性原则。
确定属性权重的方法有主观赋权法、客观赋权法和主客观相结合的赋权方法。客观赋权法基于决策矩阵信息,从问题数据入手,通过建立一定的数学模型计算出权重系数,从而减少了决策者的主观因素,具有较强的科学性。针对采用连续值、区间数、模糊数、序数等数值形式定量表达的属性值,或者用语言形式定性描述的属性值,目前主要有主成分分析法[2]、离差最大化方法[3, 4]、均方差法[5]、多目标规划法[6]、信息熵法[7, 8]、聚类分析法[9]、粗糙集方法[10]、灰色关联分析方法[11]等客观赋权法。
对于没有任何先验信息,属性值为连续值且无单一决策属性的多属性决策问题,一些文献提出了基于模糊聚类和粗糙集的客观赋权法[12, 13, 14, 15]。其核心是根据样本集的属性进行模糊聚类,以没有删除任何属性的分类为基准,把没有删除任何一个属性视为一种知识分类,将删除各个属性后视为另一种知识分类,计算删除各属性后的分类相对于总的属性分类的正域,从而求得各个属性的重要程度,最后利用归一化方法来确定各属性的权重。该方法没有客观信息的损失,具有一定的普遍性,但该方法存在以下不足:即如果样本集有m个属性,则需要进行m+1次模糊聚类计算(其中包括计算量很大的模糊相似度计算以及求出模糊等价矩阵的传递闭包计算),因此当属性数量和样本数量较多时,该方法的计算过程比较繁琐,一定程度上影响了其实用性。
粒计算理论是目前人工智能研究领域的新热点,其理论模型主要分为2类:1)以处理不确定性为主要目标,如以模糊集(也称词计算)理论和粗糙集理论为基础的模型;2)以多粒度计算为目标,如商空间理论[16, 17, 18]。这2类模型的侧重点有所不同,前者侧重于计算对象的不确定性处理,因此重点关注于含糊、不清晰概念的表达和近似推理;而后者的核心思想来源于人类问题求解的基本特征之一,即从极不相同的粒度空间上观察和分析同一问题,并很容易地从一个抽象的粒度空间转换到其他的粒度空间,也就是分层次地处理问题的能力,因此更关注于如何从不同粗细粒度的问题空间,即从不同的层次得到对问题不同角度的理解,并最终综合成对问题总的理解。
本文基于2类粒计算理论模型的思想,同样针对属性值为连续值且无单一决策属性的多属性决策问题,提出了一种融合模糊商空间理论和粗糙集理论的客观赋权法,以期在现有研究的基础上,在保证权重确定过程合理性的前提下,降低计算复杂度,进一步提高计算结果的准确性和方法的实用性。
1 粒计算理论基础 1.1 模糊商空间理论模糊商空间理论是将模糊集合论引入经典商空间理论,利用模糊等价关系将精确粒度下的商空间理论推广到模糊粒度计算中,且所有模糊商空间全体构成一个完备半序格,从而为粒计算提供了一种有力的数学模型和工具[19, 20]。模糊商空间理论能够更好地反映人类处理不确定问题的若干特点,即信息的确定与不确定、概念的清晰与模糊都是相对的,都与问题的粒度粗细有关。
定义1[19] 设X是论域,X上的一个模糊集A是指∀x∈X,有一个指定的数μA∈[0,1],称为x对A的隶属程度,映射:μA:X→[0,1],x→μA(x)称为A的隶属函数。令T(X)表示X上一切模糊子集的集合,则T(X)实际上是由μ:X→[0,1]这个函数组成的函数空间。
定义2[19] 设R∈T(X×X),若满足
1) ∀x∈X,R(x,x)=1,
2) ∀x,y∈X,R(x,y)=R(y,x),
3) ∀x,y,z∈X,R(x,z)≥supy(min(R(x,y),R(y,z)),
则称R是X上的一个模糊等价关系。
命题1[19] 设R是X上的一个模糊等价关系,令Rλ={(x,y)|R(x,y)≥λ},0≤λ≤1,则Rλ是X上的一个普通等价关系,称Rλ为R的截关系。令等价关系Rλ对应的商空间为X(λ),可得到如下性质:若0≤λ2≤λ1≤1⇔Rλ1>Rλ2⇔X(λ2)是X(λ1)的商集。于是,商空间族{X(λ)|0≤λ≤1}按照商集的包含关系构成一个有序链,称{X(λ)|0≤λ≤1}为X上的一个分层递阶结构。
命题2[19] 给定X上的一个模糊等价关系,则对应一个X上的分层递阶结构。
1.2 粗糙集理论粗糙集理论是一种处理模糊性和不精确性问题的数学工具[21, 22]。其本质思想是利用等价关系(不可分辨关系)建立论域的一个划分,得到不可区分的等价类,从而构建一个近似空间。在此近似空间上,用精确的上近似集和下近似集来逼近一个边界模糊的集合。
定义3[21] 给定一个信息系统S=〈U,A,V,f〉,其中U为研究对象的非空有限集合,称为论域;A为属性的非空有限集合,A=C∪D,其中C为条件属性集,D为决策属性集;V是属性值的集合,V=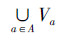 ,Va是属性a的值域;f为信息函数,f:U×A→V,它为每个对象的每个属性赋予信息值。对于每个子集X⊆U和一个等价关系R∈ind(S),称
,Va是属性a的值域;f为信息函数,f:U×A→V,它为每个对象的每个属性赋予信息值。对于每个子集X⊆U和一个等价关系R∈ind(S),称 =∪{Yi∈U/R|Yi⊆X}为X的R下近似集。
=∪{Yi∈U/R|Yi⊆X}为X的R下近似集。
定义4[21] 条件属性集C与决策属性集D之间的依赖程度γ(C,D)定义为

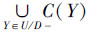 ,其表示根据条件属性集C能够被准确地分入由决策属性D所确定的分类元素的集合。
,其表示根据条件属性集C能够被准确地分入由决策属性D所确定的分类元素的集合。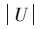 表示整个集合对象的个数。
表示整个集合对象的个数。
定义5[21] 设ak为条件属性集C中的一个条件属性(即ak∈C),属性ak关于D的重要度定义为

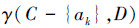 表示在C中缺少属性ak后,条件属性集对决策属性集的依赖程度。
2 融合模糊商空间和粗糙集理论的属性权重确定方法
2.1 学术思想
表示在C中缺少属性ak后,条件属性集对决策属性集的依赖程度。
2 融合模糊商空间和粗糙集理论的属性权重确定方法
2.1 学术思想
可以看出,模糊商空间理论和粗糙集理论的共同点是都认为概念粒子可以用子集来表示,不同粒度下的粒子用不同大小的子集来描述,所有的粒子都通过等价关系获得划分产生[17]。但它们之间的区别主要在于:粗糙集理论的研究对象是由一个多值属性集合描述的对象集合,但其论域是点集,各个对象之间没有结构关系或拓扑关系;而模糊商空间理论是把商集作为描述不同粒度世界的数学模型,其本质是分层递阶结构,是一种由粗到细、由表及里来描述样本集的方法,因此利用模糊商空间理论可以从大量的样本数据中建立一系列具有粒度层次结构的商空间(即对论域进行不同的划分),然后在各商空间中获取相应的知识,从而实现从模糊信息粒结构到分层递阶结构再到具有粒度结构的知识的相互转化。从这个意义上来说,模糊商空间理论可以看成是一种宏观的粒计算模型,而粗糙集理论可以看成是一种微观的粒计算模型,即不同粒度均在同一个给定的商空间中进行划分,是无拓扑结构情况的商空间特例[17]。
基于以上分析,本文所提出的融合模糊商空间理论和粗糙集理论的属性权重确定方法的主要思想是:首先根据样本集的属性值,通过应用模糊商空间理论得到具有分层递阶结构的商空间族{X(λ)|0≤λ≤1},并把一系列粒度商空间的样本聚类结果作为相应粒度空间下单一决策属性的分类;然后在各个粒度商空间X(λ)下,通过采用粗糙集理论的属性重要度计算方法得出该商空间下各个属性的重要度值,即从不同粗细粒度的商空间来观察分析各个属性的重要程度,从而综合得出各属性总的重要度;最终采用归一化方法来求解各属性的权重。这样通过将宏观和微观的粒计算理论模型统一起来,从多粒度、多层次所得到的属性重要度融合信息,使属性权重的确定过程更为全面客观,计算结果也相对更为准确。
2.2 流程步骤该方法的流程如图 1所示。
 |
| 图 1 融合模糊商空间和粗糙集理论的属性权重确定流程Fig. 1 Flow chart of ascertaining attributes weight |
其计算步骤如下:
1) 根据需要处理的样本对象属性(指标)项目,设有待处理的n个样本的组成集合
X={x1,x2,…,xi,…,xn},每个样本用m个指标特征值向量表示:xi={yi1,yi2,…,yik,…,yim},这样就可以构建一个样本初始属性表,如表 1所示。
| 样本 | 条件属性集 | |||||
| a1 | a2 | … | ak | … | am | |
| x1 | y11 | y12 | … | y1k | … | y1m |
| x2 | y21 | y22 | … | y2k | … | y2m |
| | | | … | | … | |
| xi | yi1 | yi2 | … | yik | … | yim |
| | | | … | | … | |
| xn | yn1 | yn2 | … | ynk | … | ynm |
2)由于样本初始属性表中各属性的量纲不同、取值范围不同和极性不同,因此必须首先采用线性比例变换法、极差变换法、比重变换法、向量标准化法等方法,消除属性量纲和数量级的影响,并进行极性转换,将属性值统一规范到固定的区间上,使得多个属性能够进行比较。
3)并行的计算步骤,即一方面基于模糊商空间理论,为创建具有分层递阶结构的商空间族,需采用数量积法、相关系数法、夹角余弦法、最大最小法、算术平均最小法等方法根据规范化处理后的属性值计算样本xi与xj之间的相似关系R(xi,xj)= ,构建所有样本的模糊相似矩阵R=[rij]n×n,由于rij=rji,所以R既是自反矩阵也是对称矩阵,如式(3)所示。
,构建所有样本的模糊相似矩阵R=[rij]n×n,由于rij=rji,所以R既是自反矩阵也是对称矩阵,如式(3)所示。

同时,由于粗糙集理论只能分析离散型属性值,因此需要对连续量属性值进行离散化处理。
4)该步骤同样为并行的计算步骤,即一方面需根据得到的样本集模糊相似矩阵创建具有分层递阶结构的商空间族,另一方面需根据离散化后的样本属性表分析删除各个属性后的等价类U/ind(C-{ak})。
传统的模糊聚类方法在建立模糊相似矩阵R后,需要采用平方法求出R的传递闭包:R→R2→(R2)2→…→R2K=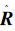 ,将R改造成模糊等价矩阵
,将R改造成模糊等价矩阵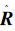 后才能得到聚类结果[23]。文献[24]证明了一个模糊相似矩阵R和其模糊等价矩阵
后才能得到聚类结果[23]。文献[24]证明了一个模糊相似矩阵R和其模糊等价矩阵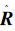 所分别对应的分层递阶结构是相同的,从而省去了比较繁琐的传递闭包计算,同时给出了基于模糊相似矩阵的分层递阶结构聚类算法,由此就可以得到一个具有商集包含关系的样本商空间族{X(λ)|0≤λ≤1}。不同的λ取值将分别对应一个不同粒度的商空间,且λ值越大,商空间的粒度就越细,样本聚类数也就越多。
所分别对应的分层递阶结构是相同的,从而省去了比较繁琐的传递闭包计算,同时给出了基于模糊相似矩阵的分层递阶结构聚类算法,由此就可以得到一个具有商集包含关系的样本商空间族{X(λ)|0≤λ≤1}。不同的λ取值将分别对应一个不同粒度的商空间,且λ值越大,商空间的粒度就越细,样本聚类数也就越多。
5)以商空间族{X(λ)|0≤λ≤1}所形成的一系列粒度商空间的样本聚类结果作为相应粒度空间下单一决策属性的分类,按照式(2)分别计算各粒度商空间下各个属性的重要度。
6) 根据式(4)计算得出各属性最终重要度:
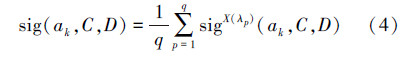
7)根据各个属性最终重要度的大小,采用归一化方法确定各属性的权重,如式(5)所示。
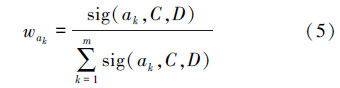
将上述提出的属性权重确定方法应用于某多品种小批量制造企业加工中心操作工2012年工作绩效综合评价,共选取15个操作人员样本,评价指标及其属性值如表 2所示,其中除加班时间为成本型属性外,其余属性均为效益型属性。
|
操作工 编号 | 总工时 a1 | 生产 工时率 a2/% | 产品 合格率 a3/% | 按期 完成率 a4/% | 加工 难度 a5 | 加班 时间 a6 |
| x1 | 3 681.0 | 99.6 | 100 | 98.70 | 高 | 294.5 |
| x2 | 3 135.6 | 96.5 | 99.65 | 100 | 较高 | 509.0 |
| x3 | 1 916.5 | 97.0 | 99.39 | 97.01 | 一般 | 277.1 |
| x4 | 4 098.0 | 98.7 | 99.05 | 96.23 | 高 | 601.8 |
| x5 | 2 076.9 | 98.1 | 99.96 | 97.92 | 较高 | 532.2 |
| x6 | 3 937.6 | 99.0 | 95.67 | 95.58 | 高 | 462.6 |
| x7 | 4 194.3 | 98.3 | 98.92 | 94.67 | 较高 | 711.9 |
| x8 | 3 456.4 | 98.4 | 99.78 | 98.31 | 较高 | 346.7 |
| x9 | 4 515.1 | 99.2 | 100 | 100 | 较高 | 543.8 |
| x10 | 2 365.6 | 100 | 97.53 | 100 | 一般 | 132.2 |
| x11 | 2 654.3 | 96.9 | 99.74 | 87.00 | 一般 | 259.7 |
| x12 | 2 975.2 | 87.0 | 100 | 99.61 | 高 | 387.3 |
| x13 | 3 777.2 | 99.0 | 100 | 99.87 | 较高 | 474.2 |
| x14 | 4 354.7 | 99.5 | 99.91 | 94.02 | 高 | 636.5 |
| x15 | 1 306.9 | 95.3 | 99.91 | 98.44 | 一般 | 375.7 |
1)由于"加工难度"属性为定性指标,直接按照"高=100,较高=50,一般=0"的规则进行处理。对于其余连续型属性值,采用式(6)所示的极差变换法进行属性规范化处理,将每一个属性值统一于同一数值范围[0,100],规范化后的属性数据表如表 3所示。
| 样本 | a1 | a2 | a3 | a4 | a5 | a6 |
| x1 | 74 | 97 | 100 | 90 | 100 | 72 |
| x2 | 57 | 73 | 92 | 100 | 50 | 35 |
| x3 | 19 | 77 | 86 | 77 | 0 | 75 |
| x4 | 87 | 90 | 78 | 71 | 100 | 19 |
| x5 | 24 | 85 | 99 | 84 | 50 | 31 |
| x6 | 82 | 92 | 0 | 66 | 100 | 43 |
| x7 | 90 | 87 | 75 | 59 | 50 | 0 |
| x8 | 67 | 88 | 95 | 87 | 50 | 63 |
| x9 | 100 | 94 | 100 | 100 | 50 | 29 |
| x10 | 33 | 100 | 43 | 100 | 0 | 100 |
| x11 | 42 | 76 | 94 | 0 | 0 | 78 |
| x12 | 52 | 0 | 100 | 97 | 100 | 56 |
| x13 | 77 | 92 | 100 | 99 | 50 | 41 |
| x14 | 95 | 96 | 98 | 54 | 100 | 13 |
| x15 | 0 | 64 | 98 | 88 | 0 | 58 |
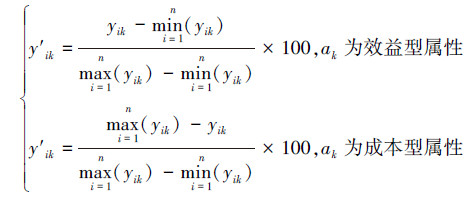
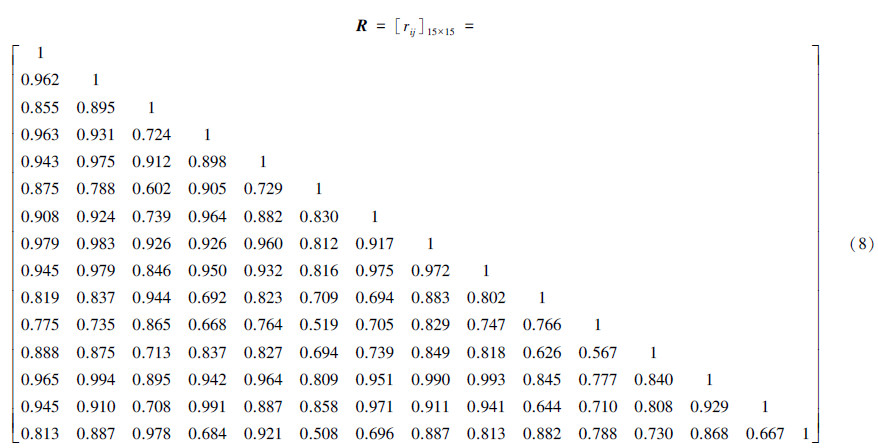
2)采用夹角余弦法计算每一个样本之间的相似关系,其计算公式如式(7)所示,从而建立所有样本的模糊相似矩阵,如式(8)所示。
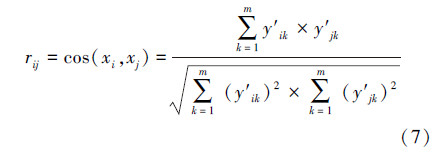
3) 根据文献[24]给出的基于模糊相似矩阵的分层递阶结构聚类算法,得到一个有序的样本商空间族{X(λ)|0≤λ≤1},不同粒度的商空间分别对应不同的样本聚类结果,如表 4所示。图 2所示为与表 4相对应的根据分层递阶结构绘制的样本聚类结构图。
| 商空间族 | 样本聚类结果 | 聚类数 |
| X(1) | {{x1},{x2},{x3},{x4},{x5},{x6},{x7},{x8},{x9},{x10},{x11},{x12},{x13},{x14},{x15}} | 15 |
| X(0.994) | {{x1},{x2,x13},{x3},{x4},{x5},{x6},{x7},{x8},{x9},{x10},{x11},{x12},{x14},{x15}} | 14 |
| X(0.993) | {{x1},{x2,x9,x13},{x3},{x4},{x5},{x6},{x7},{x8},{x10},{x11},{x12},{x14},{x15}} | 13 |
| X(0.991) | {{x1},{x2,x9,x13},{x3},{x4,x14},{x5},{x6},{x7},{x8},{x10},{x11},{x12},{x15}} | 12 |
| X(0.990) | {{x1},{x2,x8,x9,x13},{x3},{x4,x14},{x5},{x6},{x7},{x10},{x11},{x12},{x15}} | 11 |
| X(0.979) | {{x1,x2,x8,x9,x13},{x3},{x4,x14},{x5},{x6},{x7},{x10},{x11},{x12},{x15}} | 10 |
| X(0.978) | {{x1,x2,x8,x9,x13},{x3,x15},{x4,x14},{x5},{x6},{x7},{x10},{x11},{x12}} | 9 |
| X(0.975) | {{x1,x2,x5,x7,x8,x9,x13},{x3,x15},{x4,x14},{x6},{x10},{x11},{x12}} | 7 |
| X(0.971) | {{x1,x2,x4,x5,x7,x8,x9,x13,x14},{x3,x15},{x6},{x10},{x11},{x12}} | 6 |
| X(0.944) | {{x1,x2,x4,x5,x7,x8,x9,x13,x14},{x3,x10,x15},{x6},{x11},{x12}} | 5 |
| X(0.926) | {{x1,x2,x3,x4,x5,x7,x8,x9,x10,x13,x14,x15},{x6},{x11},{x12}} | 4 |
| X(0.905) | {{x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x13,x14,x15},{x11},{x12}} | 3 |
| X(0.888) | {{x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x12,x13,x14,x15},{x11}} | 2 |
| X(0.865) | {{x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15}} | 1 |
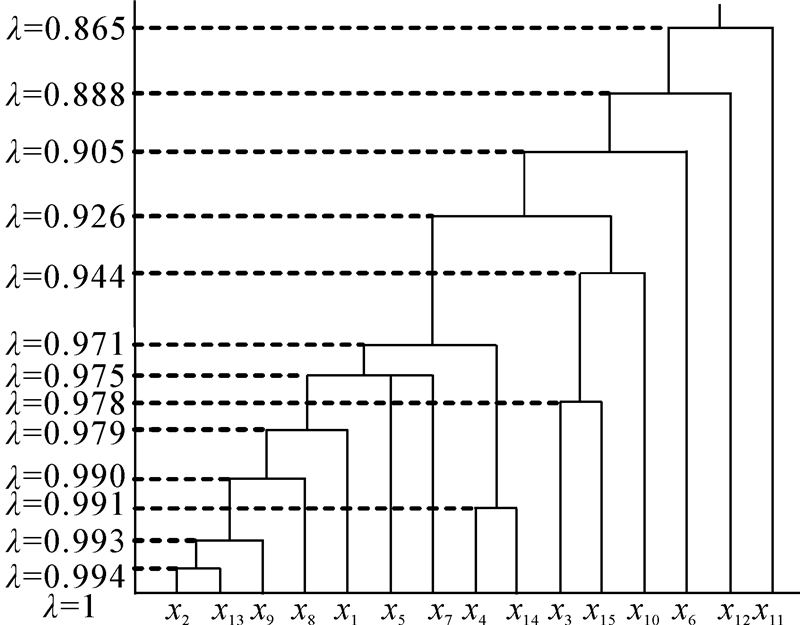 |
| 图 2 样本聚类结构图Fig. 2The structural clustering graph |
4)按照表 5中的离散区间对表 3中的属性值进行离散化处理,得到具有离散化属性值的属性表,如表 6所示。根据表 6,可以分析计算删除各个属性后的等价类。
| y′ik | [0,50) | [50,80] | (80,100] |
| 离散值 | 1 | 2 | 3 |
| 含义 | 低 | 中等 | 高 |
| U | a1 | a2 | a3 | a4 | a5 | a6 |
| x1 | 2 | 3 | 3 | 3 | 3 | 2 |
| x2 | 2 | 2 | 3 | 3 | 2 | 1 |
| x3 | 1 | 2 | 3 | 2 | 1 | 2 |
| x4 | 3 | 3 | 2 | 2 | 3 | 1 |
| x5 | 1 | 3 | 3 | 3 | 2 | 1 |
| x6 | 3 | 3 | 1 | 2 | 3 | 1 |
| x7 | 3 | 3 | 2 | 2 | 2 | 1 |
| x8 | 2 | 3 | 3 | 3 | 2 | 2 |
| x9 | 3 | 3 | 3 | 3 | 2 | 1 |
| x10 | 1 | 3 | 1 | 3 | 1 | 3 |
| x11 | 1 | 2 | 3 | 1 | 1 | 2 |
| x12 | 2 | 1 | 3 | 3 | 3 | 2 |
| x13 | 2 | 3 | 3 | 3 | 2 | 1 |
| x14 | 3 | 3 | 3 | 2 | 3 | 1 |
| x15 | 1 | 2 | 3 | 3 | 1 | 2 |

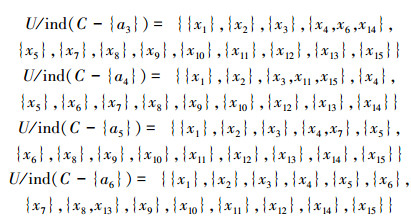
5)以表 4中商空间族所形成的14个不同粒度商空间的样本聚类结果作为相应粒度空间下单一决策属性的分类,按照式(2)分别计算各粒度空间下各个属性的重要度,再根据式(4)综合计算得出各属性的最终重要度,计算结果如表 7所示。
| 序号 | 商空间族 | 属性重要度 | |||||
| a1 | a2 | a3 | a4 | a5 | a6 | ||
| 1 | X(1) | 3/15 | 4/15 | 3/15 | 3/15 | 2/15 | 2/15 |
| 2 | X(0.994) | 3/15 | 2/15 | 3/15 | 3/15 | 2/15 | 2/15 |
| 3 | X(0.993) | 3/15 | 2/15 | 3/15 | 3/15 | 2/15 | 2/15 |
| 4 | X(0.991) | 3/15 | 2/15 | 3/15 | 3/15 | 2/15 | 2/15 |
| 5 | X(0.990) | 3/15 | 2/15 | 3/15 | 3/15 | 2/15 | 0 |
| 6 | X(0.979) | 3/15 | 2/15 | 3/15 | 3/15 | 2/15 | 0 |
| 7 | X(0.978) | 3/15 | 2/15 | 3/15 | 3/15 | 2/15 | 0 |
| 8 | X(0.975) | 0 | 2/15 | 3/15 | 3/15 | 2/15 | 0 |
| 9 | X(0.971) | 0 | 2/15 | 3/15 | 3/15 | 0 | 0 |
| 10 | X(0.944) | 0 | 2/15 | 3/15 | 3/15 | 0 | 0 |
| 11 | X(0.926) | 0 | 2/15 | 3/15 | 3/15 | 0 | 0 |
| 12 | X(0.905) | 0 | 2/15 | 0 | 3/15 | 0 | 0 |
| 13 | X(0.888) | 0 | 0 | 0 | 3/15 | 0 | 0 |
| 14 | X(0.865) | 0 | 0 | 0 | 0 | 0 | 0 |
| 综合值 | 0.1 | 0.124 | 0.157 | 0.186 | 0.076 | 0.038 | |
6)按照式(5)确定各属性的权重:wa1=0.147,wa2=0.182,wa3=0.230,wa4=0.273,wa5=0.112,wa6=0.056。由计算结果可以看出,各属性的权重由大到小的排列顺序为:按期完成率>产品合格率>生产工时率>总工时>加工难度>加班时间,这与该企业管理者正从以前单纯强调工作量和加班时间,逐步转变为更加重视任务进度的控制、产品质量的稳定、工作效率的提高这一技能人员工作绩效考核评价新思路是完全吻合的,实现了基于数据驱动的客观权重计算与决策者主观偏好的有机统一,由此初步验证了本文所提出方法的合理性和有效性。
7)为进一步验证该方法的准确性和实用性,采用文献[12, 13, 14, 15]所提出方法进行了属性权重计算(由于篇幅所限,本文不给出详细的计算过程)。其计算结果为:wa1=0.141,wa2=0.172,wa3=0.176,wa4=0.191,wa5=0.190,wa6=0.130,即各属性的权重由大到小的排列顺序为:按期完成率>加工难度>产品合格率>生产工时率>总工时>加班时间。通过对比可知,2种方法属性权重计算结果的总体分布是基本一致的,但本文方法的准确性和实用性主要体现在:①以往方法的属性权重计算结果相对比较平均,差距不大,其标准差仅为0.023,因此对企业管理者新的考核评价思路的体现作用不显著;而本文方法的权重标准差为0.072,为以往方法的3.1倍,相比较而言,更能充分发挥管理者所重视指标的导向作用。②2种方法对于"加工难度"指标权重的计算结果差异较大。考虑到"加工难度"仅仅是个定性指标,目前还难以量化,区分度不强,如果权重过大,在具体实施时将很难操作,因此本文方法相对较低的权重是比较合适的。③本文方法的模糊相似度计算次数仅为以往方法的1/7,且无需进行以往方法求出模糊等价矩阵的7×4次传递闭包计算,因此计算量要小得多。
4 结束语针对属性值为连续值且无单一决策属性的多属性决策问题,提出了一种基于粒计算的属性权重确定方法。与目前的研究成果相比,该方法通过从不同粗细粒度的商空间多角度、多层次地综合分析各个属性的重要程度,使属性权重的确定过程更为全面,计算结果更为准确,应用实例也说明了其合理性和有效性。同时,该方法只需进行一次模糊相似度计算,无需进行传递闭包计算,计算复杂度大幅降低,因此也更具实用性。方法的不足之处主要在于连续属性值的离散化处理过程会造成一定的客观信息的损失,所以如何应用合适的高效离散化算法来减少这种损失需要做进一步的研究。
| [1] | 张荣.交互式不确定多属性决策研究[M].郑州:河南大学出版社,2011:10-23. |
| [2] | 杨立才,张朋飞,王德伟.基于主成分分析的代谢综合征模糊综合评价方法[J].生物医学工程学杂志,2013,30(1):67-70.YANG Licai,ZHANG Pengfei,WANG Dewei.Fuzzy comprehensive evaluation method of metabolic syndrome based on PCA[J].Journal of Biomedical Engineering,2013,30(1):67-70. |
| [3] | XU Zeshui,ZHANG Xiaolu.Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information[J].Knowledge-Based Systems,2013,52:53-64. |
| [4] | 黄宗盛,胡培,聂佳佳.基于离差最大化的交叉效率评价方法[J].运筹与管理,2012,21(6):177-181.HUANG Zongsheng,HU Pei,NIE Jiajia.Cross efficiency evaluation method based on maximizing deviations[J].Operations Research and Management Science,2012,21(6):177-181. |
| [5] | 江文奇.无量纲化方法对属性权重影响的敏感性和方案保序[J].系统工程与电子技术,2012,34(12):2520-2523.JIANG Wenqi.Sensibility and alternative COP analysis of dimensionless methods on effect of attribute weight[J].Systems Engineering and Electronics,2012,34(12):2520-2523. |
| [6] | 刘勇,JEFFREY F,刘思峰,等.基于区间直觉模糊的动态多属性灰色关联决策方法[J].控制与决策,2013,28(9):1303-1308.LIU Yong,JEFFREY F,LIU Sifeng,et al.Dynamic multiple attribute grey incidence decision making method based on interval valued intuitionisitc fuzzy number[J].Control and Decision,2013,28(9):1303-1308. |
| [7] | CHEN Yuan,LI Bing.Dynamic multi-attribute decision making model based on triangular intuitionistic fuzzy numbers[J].Scientia Iranica,2011,18(2):268-274. |
| [8] | 陈晓红,戴子敬,刘翔.基于熵和关联系数的区间直觉模糊决策方法[J].系统工程与电子技术,2013,35(4):791-795.CHEN Xiaohong,DAI Zijing,LIU Xiang.Approach to interval-valued intuitionistic fuzzy decision making based on entropy and correlation coefficient[J].Systems Engineering and Electronics,2013,35(4):791-795. |
| [9] | 迟国泰,程砚秋,曹勇.基于聚类赋权的科学发展评价模型及实证[J].运筹与管理,2011,20(5):94-102.CHI Guotai,CHENG Yanqiu,CAO Yong.The scientific development evaluation model based on clustering and its empirical study[J].Operations Research and Management Science,2011,20(5):94-102. |
| [10] | 苏永华,刘科伟,张进华.基于粗糙集重心理论的公路隧道塌方风险分析[J].湖南大学学报:自然科学版,2013,40(1):21-26.SU Yonghua,LIU Kewei,ZHANG Jinhua.Fuzzy evaluation of collapse incidents in highway tunnel construction based on rough set and barycenter theory[J].Journal of Hunan University:Natural Sciences,2013,40(1):21-26. |
| [11] | WEI Guiwu.Gray relational analysis method for intuitionistic fuzzy multiple attribute decision making[J].Expert Systems with Applications,2011,38(9):11671-11677. |
| [12] | 黄定轩,武振业,宗蕴璋.基于属性重要性的多属性客观权重分配方法[J].系统工程理论方法应用,2004,13(3):203-207.HUANG Dingxuan,WU Zhenye,ZONG Yunzhang.An impersonal multi-attribute weight allocation method based on attribute importance[J].Systems Engineering-Theory Methodology Applications,2004,13(3):203-207. |
| [13] | 柳炳祥,李海林.基于模糊粗糙集的因素权重分配方法[J].控制与决策,2007,22(12):1437-1440.LIU Bingxiang,LI Hailin.Method of factor weights allocation based on combination of fuzzy and rough set[J].Control and Decision,2007,22(12):1437-1440. |
| [14] | 刘文军.连续值域决策表的一种属性权重确定方法[J].模糊系统与数学,2008,22(3):160-166.LIU Wenjun.An algorithm of obtain weight of continuous attributes in continuous domain decision table[J].Fuzzy Systems and Mathematics,2008,22(3):160-166. |
| [15] | 吴静,吴晓燕,高忠长.基于模糊聚类和粗糙集的仿真可信性模糊综合评估[J].系统工程与电子技术,2010,32(4):770-773.WU Jing,WU Xiaoyan,GAO Zhongchang.Fuzzy comprehensive evaluation of simulation credibility based on fuzzy clustering analysis and rough sets theory[J].Systems Engineering and Electronics,2010,32(4):770-773. |
| [16] | 张钹,张铃.粒计算未来发展方向探讨[J].重庆邮电大学学报:自然科学版,2010,22(5):538-540.ZHANG Bo,ZHANG Ling.Discussion on future development of granular computing[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2010,22(5):538-540. |
| [17] | 王国胤,张清华,胡军.粒计算研究综述[J].智能系统学报,2007,2(6):8-26.WANG Guoyin,ZHANG Qinghua,HU Jun.An overview of granular computing[J].CAAI Transactions on Intelligent Systems,2007,2(6):8-26. |
| [18] | SANKAR K P,SAROJ K M.Natural computing:a problem solving paradigm with granular information processing[J].Applied Soft Computing,2013,13(9):3944-3955. |
| [19] | 张铃,张钹.模糊商空间理论(模糊粒度计算方法)[J].软件学报,2003,14(4):770-776.ZHANG Ling,ZHANG Bo.Theory of fuzzy quotient space (methods of fuzzy granular computing)[J].Journal of Software,2003,14(4):770-776. |
| [20] | ZHANG Ling,ZHANG Bo.The structure analysis of fuzzy sets[J].International Journal of Approximate Reasoning,2005,40(1/2):92-108. |
| [21] | 苗夺谦,李道国.粗糙集理论、算法与应用[M].北京:清华大学出版社,2008:24-81.MIAO Duoqian,LI Daoguo.Rough sets theory,algorithms and applications[M].Beijing:Tsinghua University Press,2008:24-81. |
| [22] | 王国胤,姚一豫,于洪.粗糙集理论与应用研究综述[J].计算机学报,2009,32(7):1229-1246.WANG Guoyin,YAO Yiyu,YU Hong.A survey on rough set theory and applications[J].Chinese Journal of Computer,2009,32(7):1229-1246. |
| [23] | 杨纶标,高英仪.模糊数学原理及应用[M].4版.广州:华南理工大学出版社,2008:66-77. |
| [24] | TANG Xuqing,ZHU Ping,CHENG Jiaxing.Cluster analysis based on fuzzy quotient space[J].Journal of Software,2008,19(4):861-868. |



