在使用图像采集设备对图像进行采集、传输、存储和转换的过程中,因受到各种环境因素的影响会不可避免地产生噪声。图像噪声过多将对图像的后期处理造成连锁式的不良影响,因此图像去噪是图像处理中的一个重要研究方向。目前的多数去噪算法主要基于空域或频域,前者直接处理原图像像素的灰度值,后者则是对图像的频域系数进行相应处理,本文的算法属于后者。在基于频域的去噪算法中,阈值去噪法是最常用的,Donoho在文献[1]提出了经典的小波阈值去噪算法,在该算法中,对阈值的计算是通过在频域中估计分解系数的噪声标准差来完成的。一般情况下,小波阈值去噪算法的理论框架可以直接应用在超小波去噪算法上并能取得良好的去噪效果,如曲波去噪[2]、轮廓波去噪[3]等,但当含噪图像细节成分较多时,由于噪声对图像细节干扰较大,导致文献[1]的阈值计算方法准确度变低,去噪效果变差。
而目前的噪声标准差估计方法除了文献[1]方法以外,更多的是基于空域的,主要有滤波法[4, 5]、分块标准差法[6, 7]以及改进的自适应分块法[8]。滤波法是用噪声图像与滤波去噪后的图像相减得到近似纯噪声图像来近似估计噪声大小,当图像中含有较多边缘细节信息时,滤波法的精确度会大为下降。分块标准差法则是将噪声图像分割成很多子块,对每个子块进行噪声标准差估计,然后再用直方图法估计原始图像的噪声标准差。该方法计算速度快,但是容易因图像的复杂细节分布而得不到稳健的标准差估计值。文献[8]给出了一种改进的分块法,该方法采用自适应调节子块大小的选取规则对灰度均匀子块进行选取,对多种类型的图像噪声估计都取得了良好的效果,但其计算复杂度较高。本文同样采用分块法对噪声标准差进行估计,针对普通分块法的缺点,考虑对图像子块进行筛选,尽量选择均匀同质子块,也就是灰度值变化相对平坦的子块。为了达到这个目的,本文采用一种与滤波法结合的基于图像结构特征度度量分析的方法来筛选图像的灰度均匀子块,在得到均匀子块集合后,再采用直方图法估计噪声标准差,并用于轮廓波去噪。
1 图像结构特征度度量分析及改进图像结构特征度度量分析是Kim在2005年提出的一种新方法[10],该方法首先计算出原始图像子块的结构特征度度量,再对该度量进行一个统计假设测试,以决定子块属于图像结构子块还是均匀同质子块。这种分析方法是基于这样一种前提假设:如果该子块在最少一个方向上具有采样关系,那就属于图像结构子块;如果它在所有方向上都没有采样关系,那就属于均匀同质子块,也就是近似纯噪声子块。这个意思就是在图像结构子块中,至少存在一条明显的边缘细节,而在均匀同质子块中却没有明显的边缘细节。
图 1分别给出了2个标准差相同的图像结构子块和噪声子块,仅仅估计图像标准差是完全不能分辨它们的。
 |
| 图 1 标准差相同的噪声子块与结构子块Fig. 1 Noise block and structural block with same variance |
从这个例子可以引出2个问题:即如何估计一个图像子块是否至少在一个方向上有采样关系以及在任何一个方向上都没有采样关系。由于本文的目的是提取均匀子块求取噪声,因此后者更被关心。
假设ZN×N={xij;i=1,2,…,N,j=1,2,…,N}是原图像的图像子块,将子块像素值重新排列如下:

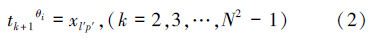
 ;l'、p'需要满足条件:
;l'、p'需要满足条件:
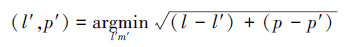
为了对Tθi有一个直观的理解,下面给出4个方向的排列形式,即对5×5的图像子块按照图 2方向重新排列。
 |
| 图 2 子块像素在4个方向上的重新排列Fig. 2 Rearrange the sub-block pixel on four directions |
重新排列之后的数据与θi的方向保持一致。定义图像结构特征向量,如式(3)所示:

设σθi2=Var(Qθi),根据文献[10],如果图像子块是均匀同质子块,则σθ12≈σθ22≈…≈σθ12。否则该子块为图像结构特征子块,据此给出如下结构特征度量公式:
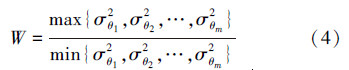
式(4)反映了图像子块结构化程度,W值越大,结构化程度越高,W值越小,结构化程度越低,即均匀同质程度越高。使用式(4)对所有的图像子块计算W值,选取百分比为α0(即置信水平)的W值较小的图像子块集合作为均匀同质子块集合,而α0是通过滤波法估计得到的。
在本文中总共计算了4个方向(见图 3),即θi={0°,90°,45°,135°}。这样式(4)可以重写为
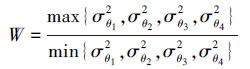
 |
| 图 3 噪声子块集合提取Fig. 3 Acquisition of noise sub-block collection |
1) 用滤波法求出原始图像的噪声标准差σl。
2) 把图像分成多个子块,分别求取标准差,并与标准差σl做比较,选取差值最小的子块,经过对多幅图像进行试验,差值区间设定为[σl-0.5×σl,σl+0.8×σl],假设符合要求的个数为ns,而子块总数为nt,比例Rα是ns/nt。对图像子块采用基于结构特征度度量分析的方法同样进行筛选,置信水平α0设定为上一步的比例Rα。
3) 对前面2步得到的子块集合取并集,得到最终的用于计算噪声标准差的子块集合。以本文采用的手指静脉图像为例,子块总数为308(图 3)。滤波法得到的子块集合为74(图 3(b));结构特征度度量分析法得到的子块集合同样为74(图 3(c)),2个子块集合的并集为116(图 3(d))。
4) 对这些子块求取标准差,并做直方图,一般来说,对上一步得到的子块集合而言,纯噪声子块的数量应该是最多的,所以在直方图中,相同噪声标准差值个数最多的值也就对应着图像的噪声标准差值,因此在这里,取直方图最高点对应的标准差值作为图像的噪声标准差值。
2.2 轮廓波去噪算法轮廓波变换是一种多分辨率多方向的图像表示方法,由M.N.Do于2002年提出[9]。它首先用拉普拉斯分解算法对图像进行多尺度分解,再用方向滤波器组将同一方向上的奇异点合成为一个系数,其基的支撑区间结构是长条形的,相比于小波变换能更稀疏地表达图像。基于轮廓波的阈值去噪算法多数是通过借鉴小波阈值去噪的理论框架来得到的,下面给出本文的去噪算法描述。
设带噪图像信号为f(m,n)=g(m,n)+σε(m,n)。其中g表示待恢复的真实图像信号,ε是高斯白噪声,σ为白噪声的标准差。设Cf为轮廓波变换系数,则去噪函数可定义为
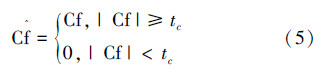
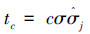 为轮廓波每个分解尺度下的系数阈值,c为可调参数,通常情况下在最细的尺度上取c=4,在其他的各个尺度上取c=3。σ为对原图像矩阵除以256后求标准差,由于轮廓波变换不是正交变换,其噪声在各个尺度上的标准差会发生变换,因此噪声在轮廓波变换各个尺度上的标准差需要用Monte Carlo仿真方法得到。即首先随机生成一定数量(可设为100)标准差σl的高斯白噪声,然后计算其轮廓波变换分解后第i尺度上标准差的估计值即为
为轮廓波每个分解尺度下的系数阈值,c为可调参数,通常情况下在最细的尺度上取c=4,在其他的各个尺度上取c=3。σ为对原图像矩阵除以256后求标准差,由于轮廓波变换不是正交变换,其噪声在各个尺度上的标准差会发生变换,因此噪声在轮廓波变换各个尺度上的标准差需要用Monte Carlo仿真方法得到。即首先随机生成一定数量(可设为100)标准差σl的高斯白噪声,然后计算其轮廓波变换分解后第i尺度上标准差的估计值即为 。而σl就是本节上一步求得的图像噪声标准差。
3 实验
3.1 图像噪声标准差估计
。而σl就是本节上一步求得的图像噪声标准差。
3 实验
3.1 图像噪声标准差估计
首先为了验证本文噪声标准差估计的有效性,基于peppers图像和baboon图像做标准差估计对比试验,即用清晰的原测试图像加上不同标准差的高斯噪声,并分别采用文献[4, 7, 8]中的方法与本文方法分别进行标准差计算,对比结果见表 1、表 2。
通过这个对比实验可以看出,在所加噪声标准差较小时,各方法求取标准差值的精度相差不大;而在噪声标准差变大的同时,本文算法的精度相对更高,这一组不同噪声标准差的图像反映了图像在不同噪声污染下的状态。由计算结果可知,本文算法在不同情况下能够保持在一个相对稳健精准的范围。
本文采用4幅不同图像作为实验对象,其中除了手指静脉图像大小为55×140,其余3幅都是500×500。标准差计算实验数据如表 3所示。
| 项目 | 手指静脉 | 指纹 | baboon | peppers |
| ns | 74 | 1204 | 925 | 2311 |
| nss | 116 | 1891 | 1493 | 3479 |
| nt | 308 | 10000 | 10000 | 10000 |
| Rα | 0.24 | 0.12 | 0.09 | 0.23 |
| Re | 0.38 | 0.19 | 0.15 | 0.35 |
| V | 17.6 | 13.7 | 26.25 | 25.97 |
表 3中,ns为滤波法与特征度量分析法筛选的子块数量,nss为近似噪声子块集合总数,nt为图像子块总数,Rα为比例ns/nt,即为置信水平α0,Re为比例nss/nt,V为最后求取的图像噪声标准差值。从表中可以看出,置信水平α0在不同的图像中取值不同,是一个动态变化的值,反映并符合图像的结构特性。本文算法对加噪图像peppers和baboon的标准差估计值与实际所加值相差不大,对原始含噪图像手指静脉与指纹的标准差估计值分别为17.6和13.7(见表 3最后一行)。
3.2 去噪对比实验在本文的图像去噪对比实验中共采用4种去噪算法与本文算法作对比,首先是2种具有代表意义的去噪算法,第1种是典型的小波阈值去噪算法[1](阈值函数为universal阈值);第2种则是由其引申出来的普通轮廓波阈值去噪算法[3]。而轮廓波去噪算法除了基于阈值去噪法以外,还有基于维纳滤波的去噪算法[11]、基于系数建模的去噪算法[12]等算法,在本文实验中将采用上述方法与本文方法进行去噪效果对比。
实验对象主要分为两大类:1) 原始含噪图像:手指静脉图像和指纹图像,在实验中各取一幅;2) 标准测试图像peppers和baboon加噪后的图像(标准差分别为5,10,15,20,25)。由于篇幅所限,在标准测试图像的去噪实验中仅给出噪声标准差为25时的去噪效果图像。
对图像质量的评价方法根据指标的不同主要分两大类:1) 主观指标,这个可以通过对去噪后的图像进行观察获得;2) 客观指标,而基于客观指标的方法则又可分为3类:全参考图像质量评价、半参考图像质量评价以及无参考图像质量评价。在本文的实验对象中,对原始含噪图像而言,由于缺乏原清晰标准图像,只能采用无参考图像质量评价方法,因此本文采用了Liu等在2014年提出的SSEQ方法[13],该方法利用局部空间熵特征和谱熵特征来描述图像质量,能够对图像质量得到较精确的评价分数。对实验中的标准测试图像peppers和baboon,本文则采用了应用范围最广的PSNR方法。
首先针对细节较少peppers图像进行去噪对比实验,下面分别给出去噪效果图(如图 4)和PNSR对比表(如表 4)。
 |
| 图 4 加噪peppers图像去噪对比实验Fig. 4 The denoising experiment of noised peppers image |
图 4的标准测试图像所加噪声强度较大,对图像造成了较大的噪声干扰。由图 4可知,小波阈值去噪和普通轮廓波去噪处理后的图像效果并不理想,而文献[12]的基于系数建模算法与本文方法去噪效果则相对较好,存在更少的絮状干扰,优于普通轮廓波去噪和小波去噪。从表 4可以得知,当所加噪声强度较小时,文献[11]、文献[12]的去噪效果都要略优于本文算法,但当噪声影响变大时,本文算法的处理效果则优于其他算法。
与peppers图像相比,baboon图像则含有更多的细节,下面是baboon图像的去噪效果图(图 5)和PNSR对比表(表 5)。
 |
| 图 5 加噪baboon图像去噪对比实验Fig. 5 The denoising experiment of noised baboon image |
对于细节较多的baboon图像来说,噪声对图像的干扰更明显,从图 5可以看出,小波阈值去噪与普通轮廓波去噪有明显的低频噪声污染,并严重丢失了部分图像细节。文献[11]与文献[12]的去噪效果要好一些,但对图像细节的还原仍然不足,本文算法在这种情况下要优于上面几种算法的去噪效果,有效克服了絮状物干扰,且更好的还原了图像的细节,这一点从表 5中也可看出。接下来对原始含噪图像:手指静脉和指纹进行对比试验。如图 6、图 7和表 6。
 |
| 图 6 原始静脉含噪图像去噪对比实验Fig. 6 The denoising experiment of original noised image |
 |
| 图 7 原始指纹含噪图像去噪对比实验Fig. 7 The denoising experiment of original noised image |
在图 6试验中,手指静脉图像噪声标准差估计为17.6,噪声污染较大,但是由于手指静脉细节较少,小波阈值去噪也取得了不错的效果,与普通轮廓波去噪效果差别不大,由于手指静脉细节较少、灰度变化平缓,难以用主观方法判别去噪效果。本文采用了Liu等提出的无参考SSEQ方法[13],该方法评价图像得到的分数范围为1~100,数值越低,代表图像质量越好。本文对原图像与各种方法去噪后图像进行SSEQ估分,结果见表 6,其结果表明本文的去噪效果略优于其他算法。指纹图像的噪声标准差估计估计为13.7,但图像细节较多,与图 5实验结果类似,小波阈值去噪和普通轮廓波去噪效果不佳,文献[11]和文献[12]方法去噪效果稍好,但仍有细节污染,相比而言,本文算法对含噪细节图像的去噪效果相对稳健,令人满意。
4 结束语本文给出了一种基于轮廓波去噪的改进算法,在用直方图法估计图像噪声标准差时,采用了新的噪声子块筛选方法,可有效筛除含有图像边缘结构信息和标准差值异常的子块,通过与参考文献中常用噪声标准差估计算法对比,本文算法准确度更高,可以更有效地对加不同噪声强度的常用测试图像进行精确估计,同时,将基于该方法算得的估计标准差值用于轮廓波去噪,效果更好,并能够在一定程度上解决轮廓波去噪中的絮状干扰等常见问题,而且在处理含较多细节的图像时也具有很好的鲁棒性,应用范围更广。
| [1] | DONOHO D L,JOHNSTONE L M.Ideal spatial adap-tation by wavelet shrinkage[J].Biometrika,1994,81(3):425-455. |
| [2] | STARCK J L,EMMANUEL C.The curvelet transform for image denoising[J].IEEE Transactions on Image Processing,2002,11(6):670-684. |
| [3] | DO M,VETTERLI M.The contourlet transform:an efficient directional multiresolution image representation[J].IEEE Transactions on Image Processing,2005,14(12):2091-2106. |
| [4] | TAI Shenchuan,YANG Shiming.A fast method for image noise estimation using Laplacian operator and adaptive edge detection[C]//Proceedings of the 2008 International Symposium on Communications,Control and Signal Processing.Valetta,Malta,2008:1077-1081. |
| [5] | CHEN Yikai,WANG Jingfa.Skew detection and reconstruction based on maximization of variance of transition counts[J].Pattern Recognition,2000,33(2):195-208. |
| [6] | 满家巨,沈军.一种图像噪声准确估计方法[J].湖南师范大学自然科学学报,2008,31(2):44-47.MAN Jiaju,SHEN Jun.A method of image noise estimate[J].Journal of Natural Science of Human Normal University,2008,31(2):44-47. |
| [7] | BILCU R,VEHVILAINEN M.A new method for noise estimation in images[C]//Proceedings of the 2005 IEEE EURASIP International Workshop on Nonlinear Signal and Image Processing.Sapporo,Japan,2005:18-20. |
| [8] | OLSEN S.Estimation of noise in images:an evaluation[J].Graphical Models and Image Processing,1993,5(4):319-323. |
| [9] | VETTERLI M D M.Contourlets:a directional multiresolution image representation[C]//2002 International Conference on Image Processing.New York,USA,2002:357-360. |
| [10] | KIM Y,LEE J.Image feature and noise detection based on statistical independent tests and their applications in image processing[J].IEEE Trans Consumer Electronics,2005,51(4):1367-1374. |
| [11] | ZHOU ZF,CAO J Z.Contourlet-based image denoising algorithm using adaptive windows[C]//IEEE Conference on Industrial and Applications.Xi'an,China,2009:3654-3657. |
| [12] | CHEN G Y,ZHU W P.Image denoising using neighbouring contourlet coefficients[C]//Advances in Neutral Networks.Beijing,China,2008:384-391. |
| [13] | LIU Lixiong,LIU Bao,Huang Hua,et al.No-reference image quality assessment based on spatial and spectral entropies[J].Signal Processing:Image Communication,2014,29(8):856-863. |



