近年来,随着静息态功能磁共振图像(rest functional magnetic resonance imaging,R-fMRI)技术的发展,研究者对大脑的探索正逐步从结构分析转为关注脑区间的功能连接,越来越多的实验也正在探索一些精神类疾病,如阿耳滋海默氏病(Alzheimer)、抑郁症(depression)、精神分裂症(schizophrenia,SZ)与患者脑内功能连接存在的联系[1, 2, 3]。机器识别技术可以从由图像数据处理得到的脑功能连接矩阵中,挖掘出可作为脑部疾病临床诊断指标的有用信息[4],但脑功能连接矩阵一般都是超高维数据,无法直接将已有的机器识别技术用于数据处理,因此传统的一些线性降维方法,如PCA (principal component analysis)、ICA (independent component analysis)等被用于数据的预处理中[5],但是这些降维方法都有各种使用限制的缺陷,使得在运用上述方法前必须假设数据符合一定的统计特性。为解决上述问题,国外H.Shen等将低维嵌入引入到对fMRI脑连接矩阵数据的分析中[6];S.Lee构建了一种高斯过程分类器来研究异常的脑功能连接[7];国内支联合等[8]基于离散小波变化,设计了一种具有高灵敏度的fMRI数据特征提取方法;王华东等[9]研究了针对事件相关fMRI数据的多尺度特征提取方法。但上述方法都局限于局部分析,无法从整体上分析脑网络的差异,导致部分重要分类信息的缺失。因此本文着重从整体研究脑功能网络,将脑功能连接矩阵考虑为图论中的无向图,运用复杂网络理论知识将图信息用一组一维特征向量表示,并将其运用在对精神类脑部疾病的机器分类研究中。
复杂网络理论是基于图论发展起来的,它将真实世界的大规模复杂系统抽象成由节点和边集构成的数学表达式,通过分析网络的拓扑结构,从而揭示原复杂系统内部的特性。而大脑作为人体最为复杂的器官,已经被证明为是一个复杂系统,使用复杂网络分析脑连接矩阵目前已成为研究的主流方法,特别是在针对没有明显病灶的精神分裂症研究中,复杂网络理论得到广泛运用。研究者发现SZ患者的脑功能连接网络相比正常被试在"小世界现象"、有效连接、聚集程度等网络特性上均存在不同程度的减弱。Yu等也发现SZ患者的脑功能网络中存在节点分布及其社团结构异常[10]。
将复杂网络运在分类研究中主要有3个优势:1) 复杂网络理论具有多种计算结构特征的方法,能够解决连接矩阵维数过高、特征提取困难的问题;2) 通过对大脑的分割脑区设置节点可以很方便地找寻到结构和功能上的联系;3) 可以在不同被试间定量比较其网络特征,便于研究脑部疾病的病理特性。
1 脑功能复杂网络 1.1 定义网络节点在脑网络分析中常用的定义节点的方法有3种:1) 将每一个体素定义为一个节点,该方法虽然可以在最大分辨率下分析脑网络,但是计算量巨大,不利于进一步研究;2) 根据体素间的空间独立性,使用ICA算法将全脑分为若干个独立成分,将每个独立成分作为节点。该方法无需任何先验知识,是一种纯数据驱动的方法,但是其分割的独立成分缺少生理学解释,很难将实验结果运用到临床治疗;3) 选用生理学解剖模板分割脑区,该方法有多种模板可选,简单高效且实验方法具有可重复性,现为多数研究者采用。因此本文选用AAL (anatomical automatic labeling)模板将全脑分为90个脑区[11],每个脑区代表脑网络中的一个独立节点,并分别提取每个节点的平均体素时间序列,定义节点时间序列矩阵为
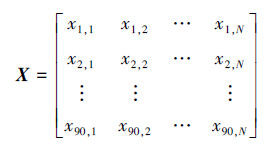
边在脑网络中常由大脑的解剖学连接、功能连接或者有效连接构成。其中功能连接代表脑区间血氧依赖水平信号变化的互相关程度,有效连接则代表脑区间因果联系。本文构建的为脑网络的无向图,传统方法为选用皮尔逊相关:
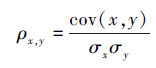
但传统皮尔逊相关无法反映时间序列细节,为克服此问题,本文选用节点间的子波相关系数作为功能连接边权值。具体算法如下:设时间序列X={xi,1,xi,2,…,xi,N}为第i脑区的平均体素时间序列,根据极大重叠离散小波变换(maximal overlap discrete wavelet transform,MODWT),设{hj,1;l=0,...,Lj-1}和{gj,1;l=0,...,Lj-1}分别为在j层的小波滤波器和尺度滤波器。其中Lj=(2j-1)(L-1)+1,L为初始滤波器的长度。设在j层的小波系数和尺度系数分别为Wj和Vj,满足
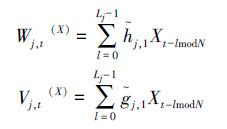
 。
。
于是有时间序列{Xt}={xi,1,xi,2,…,xi,N}和{Yt}={xj,1,xj,2,…,xj,N}分别为第i和j脑区的平均体素时间序列,它们是具有稳定增量的高斯过程,其中N≥Lj,t=0,1…,N-1。它们之间尺度相关的协方差定义为

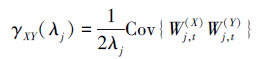
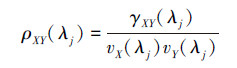
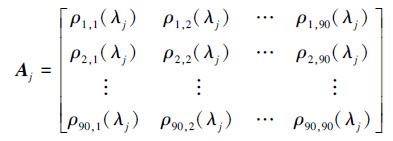
因为在复杂网络中处理的权值一般为正值,而ρij∈[-1,1],为使得连接矩阵中所有权值为正,本文使用了一种非线性变换为
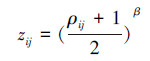
图 1为19个正常被试的脑网络稀疏度随阈值变化曲线,非线性变换在处理相关时,如图 1中所示,随着β值的升高,在原网络中权值大的边,在变换后的网络中分布区域更广,网络稀疏度的变化越来越集中于权值的前段,在同一稀疏度下,阈值更加集中,但是过大的β值使得稀疏度急速下降。因此β一般取2或者4较为适宜。
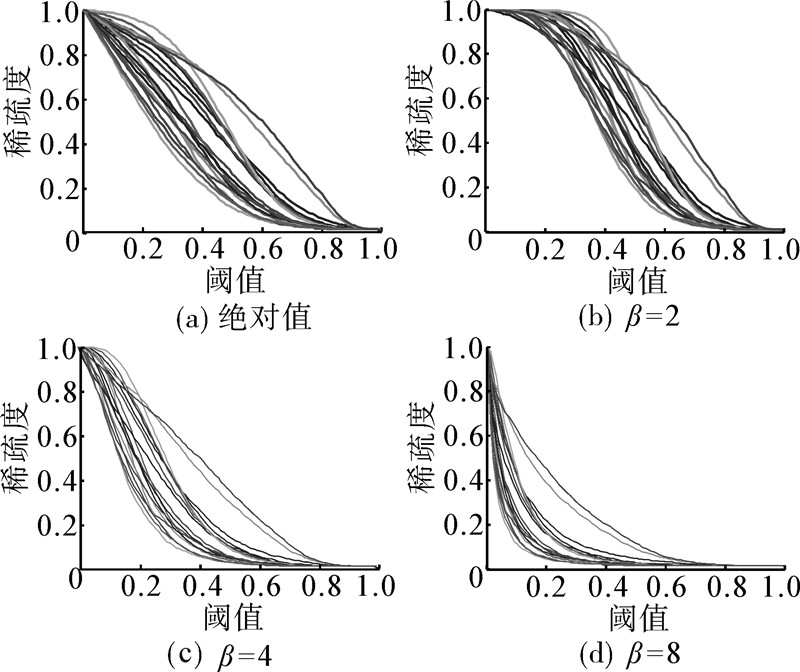 |
| 图 1 网络稀疏度随阈值变化曲线Fig. 1 The curve of network sparsity with threshold |
在以往的研究中,研究者多忽略连接矩阵内的权值,构建结构简单、特征度量计算成本小的无权网络。最近Mikal等[12]的研究表明加权网络较无权网络能更加全面地反映网络的拓扑结构特征,因此本文将根据对角矩阵分别构建这2类网络。对于加权网络,当2个脑区连接值小于阈值时,连接矩阵中相对应的权值设为0,即表示在无向图中两脑区所代表节点间没有边连接。而当两脑区连接值大于或等于阈值时,即认为两脑区存在连接且连接强度即为连接矩阵中对应的权值。无权网络与加权网络不同的是,当2个脑区的连接值大于设定阈值则存在连接,赋值为1,不存在则为0。
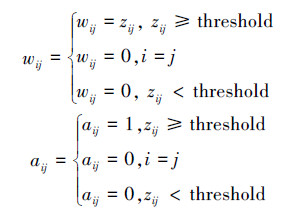
静息态脑功能连接网络包含有大量数据。本文采用90个节点共4005条边。如此超高维的数据难以用于下一步的分类识别,因此将复杂网络中对网络拓扑结构的研究成果运用于脑功能网络的降维中,用小规模的网络特征度量数据去表征结构特性,本文主要用到节点度、聚集系数、全局效率等网络特征度量。
节点度指的是与某节点相关联的边的数目,它直接反应了该节点在网络中的重要程度。无权网络和加权网络节点i的节点度分别定义为
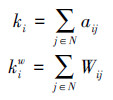
网络成本kcost衡量了网络的稀疏度,定义为

聚集系数Ci反应了该节点与其所在子网络联系的紧密性,CiW反应了环绕在节点i周边的三角形的平均强度。定义为
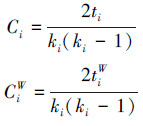
 ,ti从几何特点上来看代表着与节点i连接的三角形的数量,它们都代表着节点i的分离度。
,ti从几何特点上来看代表着与节点i连接的三角形的数量,它们都代表着节点i的分离度。
全局效率节点是逆最短路径长度的平均值并包含路径长度特征,具有较高全局效率的节点其连接距离较远节点的能力更强。定义有

阈值的选择直接影响网络的规模,当连接网络矩阵选取不同阈值时,网络规模、网络结构都会发明显变化。图 2显示了不同稀疏度时的脑功能网络。
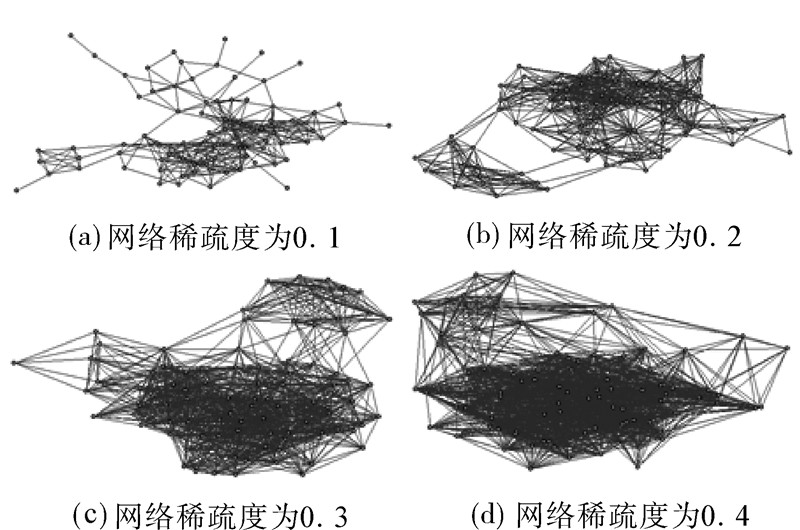 |
| 图 2 脑功能复杂网络Fig. 2 Brain function in complex networks |
很明显图 2(b)中所示网络,在网络稀疏度为0.2时,分为了2个社团部分;在稀疏度较小时,如图 2(a)中所示,网络结构不明显;当稀疏度增大到0.4时,如图 2(d)所示,网络变得密集,结构趋向于随机。对于网络来说,阈值越趋向于0,连接的边数越多其网络所含信息越多。但当网络稀疏度较大时,无权网络"小世界"特征指标趋近于数值1,整个网络结构变得没有区分度。因此选择合适的阈值对最后的分类至关重要。
本文通过以下2条规则确定阈值区间:
1) 设定阈值后必须保证所构成的网络为稀疏网络,即满足ki≥2logN≈9,即最大的阈值必须满足网络中有405条连接边确保每个节点都有连接。
2) 最小阈值应满足所构成的网络在相同的节点分布下相比随机网络具有更小的全局连接效率和更大的局部连接效率。
在以往的研究中,研究者主要根据概率分布来选定阈值,但是阈值受节点和边值计算影响,缺乏一般性[13]。因此本文选择网络连接边数为变量,以在0.06~0.12Hz尺度下为例,比较SZ患者和正常被试的静息态脑功能连接网络及同规模下的随机网络。如图 3所示,当3类网络稀疏度超过0.3时,网络结构区分度下降。综上研究,本文重点研究稀疏度在0.2~0.3间的网络。
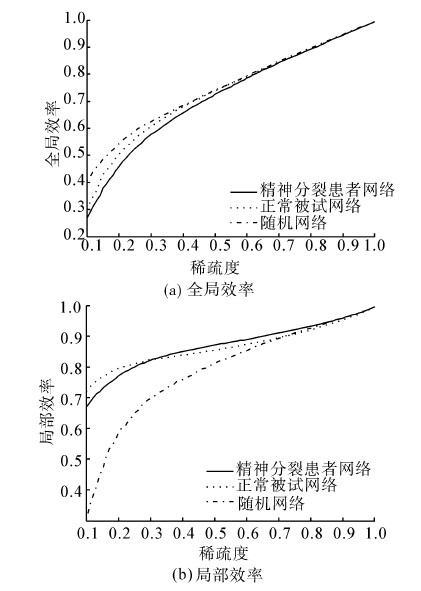 |
| 图 3 网络全局效率、局部效率随连接边数变化曲线Fig. 3The curve of network global efficiency, local efficiency increases with the number of edges connecting |
本文所用数据来源于美国奥林神经精神病研究中心。参加实验的有19个正常被试(平均年龄(31.7±9.2)和21个精神分裂症患者(平均年龄35.9±12.1)。2组被试的年龄分布没有明显差异(T检验P=0.18)。所有精神分裂症患者均经过Hartford医院临床确诊。采集静息态功能磁共振图像数据的仪器为西门子公司的Allegra 3T磁共振采集系统。功能像采用GRE-EPI序列采集,TR=1500ms,TE=27ms,FA=70°,FOV为24cm,矩阵为64×64,层厚4mm,间隔1mm。数据采用SPM8进行预处理,具体包括:时间层校正;头动校正,将扫描得到的图像标准化到SPM8所对应的标准MNI空间,并将体素重新采样为3mm×3mm×3mm (原始数据为3.75mm×3.75mm×4mm)。然后采用REST软件进行去基线漂移和滤波处理(0.01Hz < f < 0.12Hz),减少低频漂移并且过滤掉如心跳、呼吸等高频噪声。
2.2 分类精度研究本文首先将在全脑范围内定义大脑节点,使用MODWT来分解节点的平均体素时间序列,然后计算子波相关系数并分别构建无权网络和加权网络,最后提取网络结构统计向量作为机器识别特征。选用"留一法"分析2类网络在不同网络稀疏度下的分类精度,通过对SZ患者和正常被试组之间的分类研究论证所述方法的可行性。具体流程如图 4。
 |
| 图 4 本文实验仿真流程Fig. 4 The experimental simulation process |
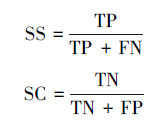
本文在选用"留一法"分别研究无权网络和加权网络的分类精度随稀疏度变化时,每次选取样本集中的一个样本作为测试样本,其余作为训练样本并重复该过程。分类精度将量化为识别率GR、灵敏度SS、特异度SC,公式为

本文在综合比较前期研究成果后,选择聚集系数作为分类脑功能网络的特征向量,于是有表示图结构信息的一维向量F= ]作为分类器的输入。图 5为尺度1(0.06~0.12Hz)、尺度2(0.03~0.06Hz)、尺度3(0.01~0.03Hz)的加权网络和无权网络在不同β值时分类精度随稀疏度变化曲线。很明显,加权网络无论在最高识别精度及识别平稳度上都优于无权网络,并且在尺度一的加权网络中在稀疏度为0.2~0.3时有着较好的识别精度。相比无权网络在3个尺度下识别精度整体上没有明显区别,加权网络的3个尺度,除了尺度3识别效果不佳外,其他2个尺度均有不错的识别效果。
]作为分类器的输入。图 5为尺度1(0.06~0.12Hz)、尺度2(0.03~0.06Hz)、尺度3(0.01~0.03Hz)的加权网络和无权网络在不同β值时分类精度随稀疏度变化曲线。很明显,加权网络无论在最高识别精度及识别平稳度上都优于无权网络,并且在尺度一的加权网络中在稀疏度为0.2~0.3时有着较好的识别精度。相比无权网络在3个尺度下识别精度整体上没有明显区别,加权网络的3个尺度,除了尺度3识别效果不佳外,其他2个尺度均有不错的识别效果。
 |
| 图 5 分类精度随稀疏度变化曲线Fig. 5 The curve of the classification accuracy with the sparsity |
表 1给出了本文算法在尺度1下,网络稀疏度为0.2~0.3时,加权网络β取不同 β值时的平均识别精度,并将其结果与其他算法对SZ患者的识别效果进行比较。数据表明本文算法具有一定的优越性,且采用非线性变换处理连接矩阵权值比采用传统的绝对值变换识别精度更高。综合衡量当β取4时与β取2时的识别精度发现,两者识别精度相差不大,但β=2时有着更好的灵敏度,其正确识别患者能力更强。综合考虑β=2时有最好的识别效果
本文运用复杂网络理论构建脑功能网络,并对精神分裂症的分类进行了仿真实验。实验结果证明,网络在不同稀疏度时识别具有差异,并且加权网络较无权网络在识别精度上具有一定的优越性。本文方法既可推广到其他脑部疾病的机器识别,也为研究异常脑区的定位打下研究基础。目前对于加权网络的拓扑结构研究成果还比较少,对于脑网络的研究理论还未成熟。相信随着复杂网络理论的发展,运用该理论识别脑功能网络的精度将得到提高,这也是有待进一步深入研究的课题。
致谢 感谢来自于美国The Mind Research Network的Yu Qingbao博士在论文撰写中的答疑;论文实验中所用的fMRI数据来自美国Hartford的Olin Neuropsychiatry研究中心。
| [1] | KOCH W,TEIPEL S,MUELLER S,et al.Diagnostic power of default mode network resting state fMRI in the detection of Alzheimer's disease[J].Neurobiology of Aging,2012,33(3):466-478. |
| [2] | 袁辉,祁吉.首次发作抑郁症患者认知功能的fMRI研究[J].临床放射学杂志,2011,30(3):304-309.YUAN Hui,QI Ji.The fMRI study of cognitive function in patients with first attack depression[J].Journal of Clinical Radiology,2011,30(3):304-309. |
| [3] | YOON J H,NGUYEN D V,MCVAY L M,et al.Automated classification of fMRI during cognitive control identifies more severely disorganized subjects with schizophrenia[J].Schizophrenia Research,2012,135(1):28-33. |
| [4] | PEREIRA F,MITCHELL T,BOTVINICK M.Machine learning classifiers and fMRI:a tutorial overview[J].Neuroimage,2009,45(1):S199-S209. |
| [5] | 蔡军,郑玲,李林,等.独立成分分析的fMRI对癫痫灶检测的对比研究[J].临床放射学杂志,2012,31(010):1370-1374.CAI Jun,ZHENG Ling,LI Lin,et al.Comparative study of independent components analysis and combined EEG functional MRI in epileptic focus detection[J].Journal of Clinical Radiology,2012,31(10):1370-1374. |
| [6] | SHEN H,WANG L,LIU Y,et al.Discriminative analysis of resting-state functional connectivity patterns of schizophrenia using low dimensional embedding of fMRI[J].Neuroimage,2010,49(4):3110-3121. |
| [7] | LEE S,ZELAYA F,SAMARASINGHE Y,et al.Data-driven fMRI group classification using connected components and Gaussian process classifiers[C]//2011 IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP).Prague,Czech Republic,2011:717-720. |
| [8] | 支联合,李玉晓,赵书俊,等.基于离散小波变换的fMRI数据特征提取[J].中国医学影像技术,2010(6):1151-1154.ZHI Lianhe,Li Yuxiao,ZHAO Shujun,et al.Feature extraction of fMRI data based on discrete wavelet transform[J].Chin J Med Imaging Technol,2010(6):1151-1154. |
| [9] | 支联合,王华东,张洁.统计参数图和多尺度特征提取用于事件相关fMRI分析的比较[J].中国生物医学工程学报,2011,30(1):135-139.ZHI Lianhe,WANG Huadong,ZHANG Jie.Comparison of SPM2 and MFE in Event-related fMRI Processing[J].Chinese Journal of Biomedical Engineering,2011,30(1):135-139. |
| [10] | YU Q,SUI J,LIU J,et al.Disrupted correlation between low frequency power and connectivity strength of resting state brain networks in schizophrenia[J].Schizophrenia Research,2013,143(1):165-171. |
| [11] | TZOURIO-MAZOYER N,LANDEAU B,PAPATHANASSIOU D,et al.Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain[J].Neuroimage,2002,15(1):273-289. |
| [12] | RUBINOV M,SPORNS O.Weight-conserving characterization of complex functional brain networks[J].Neuroimage,2011,56(4):2068-2079. |
| [13] | BRAUN U,PLICHTA M M,ESSLINGER C,et al.Test-retest reliability of resting-state connectivity network characteristics using fMRI and graph theoretical measures[J].Neuroimage,2012,59(2):1404-1412. |



