,
2. 无锡职业技术学院 物联网技术学院, 江苏 无锡 214121
,
2. School of Internet of Things Technology, Wuxi Institute of Technology, Wuxi 214121, China
概率密度估计常见的做法是根据所得数据建立概率密度函数(probability density function,PDF)，在机器学习和模式识别中具有非常重要的作用[1]，如聚类分析[2]等。通常概率密度估计法分参数估计和非参数估计2类。因真实数据概率密度分布不可知，故非参数核密度估计法(kernel density estimation,KDE)[3]是采用较广泛的方法。因KDE需要所有样本参与计算且需存储所有数据，故压缩集概率密度估计器[4]和快速压缩集概率密度估计器[5]被提出以解决存储空间和运行效率问题。上述传统的概率密度估计法效果显著但均未考虑领域间自适应学习的问题。在实际应用中存在这样的场景，已有源域数据集数据量大、密度估计精确；但相关目标域数据集由于隐私保护或数据遗失等原因只获得少量数据，这些数据是目标域真实信息但却不足以建立目标域PDF。如何既保证目标域已知数据对建立目标域PDF的作用，又能利用源域知识对目标域信息不足部分加以弥补是本文研究的重点。
1 DADE模型 1.1 DADE模型理论依据领域自适应概率密度估计器的应用前提是存在两相关领域，两域通过传统密度估计法，如Parzen窗法获得概率密度估计值，形成 (x,y) 对。其中，x 是输入向量，y 是概率密度估计值。源域 (x,y) 对足以构建概率密度函数，而出于隐私保护或数据遗失等原因，一些高度机密的数据无法获得，所得少量目标域 (x,y) 信息精确，但不足以构建目标域概率密度函数。
传统密度估计法本身不能进行领域间知识传递，本文的贡献在于使用无偏置 v-SVR 回归函数表示概率密度函数，这样做的优势在于：
1)无偏置 v-SVR 等价于CC-MEB的特性，可使用核心集[6, 7, 8]代替源域所有数据建立概率密度函数，提高密度估计效率；
2)密度回归函数 f(x) 可由CC-MEB中心点表示，提出中心点知识传递模型[9]，实现相似领域间领域自适应概率密度器的建立，若使用源域核心集代替所有源域样本表示源域中心点，还可起到源域隐私保护的目的。
1.2 DADE模型架构设训练集 T={(x1,y1),…,(xl,yl)} ，其中输入向量 xi∈Rn，输出向量 yi∈Y=R 为概率密度估计值，i=1,2,…,l 。本文用无偏置支持向量回归函数 y=wTφ(x) 建立概率密度估计函数，与传统 v-SVR 相比，没有b项，文章下面部分介绍无偏置 v-SVR 。
1.2.1 无偏置 v-SVR无偏置 v-SVR 试图寻找 Rn 上的一个实值函数 g(x) ，以便使用 y=g(x) 来推断任一输入 x 所对应的输出值 y 。通常训练集在输入空间线性不可分，故引入映射函数 φ(x) 将 xi 映射到高维空间 φ(xi) 中。 无偏置 v-SVR 原始优化问题如下：
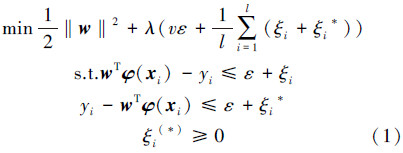
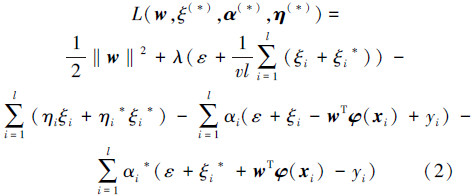
为了使式(2)最小化，对L关于向量 w 和变量 ε、ξi(*) 求偏导数，得
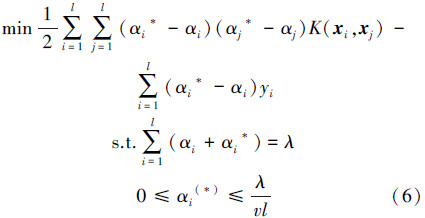
最终所得回归函数：
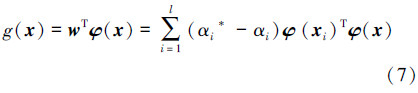
概率密度函数 p(x) 需满足 p(x)≥0 ，∫-∞+∞p(x)dx=1 的条件，但无偏置 v-SVR 进行概率密度估计时不能满足上述条件，故需添加约束
，且核函数的选择满足 K(x,x′)≥0 ，∫-∞+∞K(x,x′)dx=1。
1) CC-MEB
Tsang等在文献[6]中介绍了最小包含球(minimum enclosing ball,MEB)与中心约束最小包含球(center-constrained MEB,CC-MEB)。设 S={x1,x2,…,xm} ，其中 xi∈Rd ，MEB的思想是找到包含集合S所有样本 φ(xi) 的最小球，则属于该类的数据就在球中，不属于该类的数据就在球外。为每个 φ(xi) 增加一维 δi ，形成集合 S′={(φ(xi)′,δi)}i=1m ，将最后一维中心点坐标设为0，即中心点坐标(c,0)，则找到包含集合S’中所有样本的最小超球最优化问题为
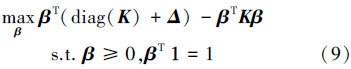
使用最优解 β ，可得到半径R、中心点c的值：
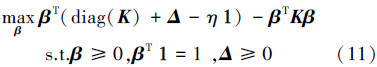
文献[6]指出，任意满足式(11)的QP问题均能看作CC-MEB问题，可运用核心集快速算法求解。把整个数据集合S的求解转化成对S的一个子集Q的求解，可得到一个精确有效的近似解，其中Q被称为核心集。具体方法参见文献[6]。
2) 无偏置 v-SVR 与CC-MEB间关系
令
，以满足
，式(12)与式(6)等价。
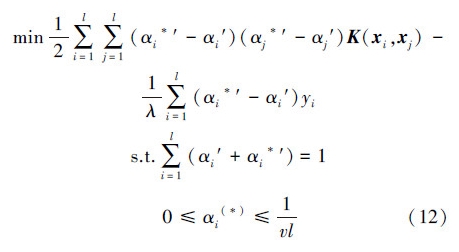
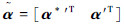，式(12)式相应的矩阵形式：
。
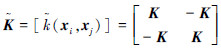式(13)为无偏置 v-SVR 的QP形式，与式(11)相比较，求 Δ 的值：
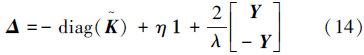
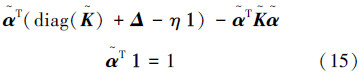
该形式用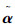
替换了β与式(11)等价，是CC-MEB问题，可使用核心集快速解法求解。
按式(15)求解，球心 c 可按下面公式计算：
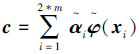
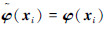，i=m+1,m+2，…,2m 时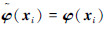，，由此可得：
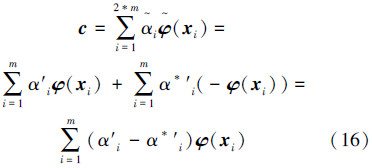
1)无偏置 v-SVR 等价于CC-MEB，故可用核心集技术进行快速求解；
2)概率密度回归曲线可由其二次规划形式等价的CC-MEB的中心点表示。
1.2.3 DADE模型从1.2.2节分析可知，无偏置 v-SVR 等价于CC-MEB，概率密度函数由CC-MEB中心点表示。在此理论基础上，本文提出通过学习源域中心点将源域知识传递给目标域，构造学习源域知识且与目标域无偏置v-SVR等价的CC-MEB，此CC-MEB的中心点可用于目标域概率密度函数的建立。
学习源域中心点的CC-MEB原始问题如下：
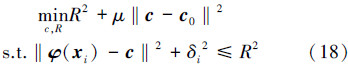
引入拉格朗日乘子变量，在约束条件下构造式(18)的拉格朗日函数：
由最优化理论可知，式(19)在鞍点处取极值，在鞍点处L关于变量c和R的偏微分：
将(20)代入(19)，该问题的对偶形式为：
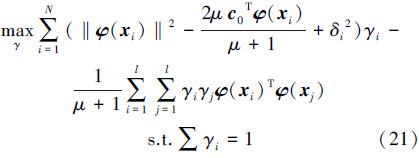
式中：
，c0 由源域无偏置 v-SVR 训练按式(16)获得，δi 由目标域样本按式(14)获得。求解式(21)二次规划，按式(20)获得中心点带入式(22)即可获得目标域概率密度回归函数：
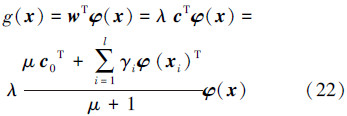
本文实验将本文所提算法与如下3个方面的回归函数进行性能对比:1)直接使用源域数据构建概率密度回归函数； 2)直接使用包含少量信息的目标域数据构建概率密度回归函数；3)使用源域、目标域数据共同构建概率密度回归函数。从而来体现本文所提算法的优势。
实验中将DADE方法与上述相关的方法进行性能比较，以目标域测试集概率密度估计精度作为评价指标，具体为：
，其中 xi表示目标域测试集元素，f(xi) 表示 xi的真实密度值，
表示各算法所得xi 概率密度估计值，N值为500。实验通过网格搜索方式确定最优参数，高斯核函数的方差h在网格
中搜索选取，其中x为训练样本平均2范数的平方根；λ参数在网格{1,2,3,4,5,6,7,8,9,10}中搜索选取；v参数在网格{1×10-4,1×10-3,1×10-2,1×10-1,1}中搜索选取；μ 参数在网格{1,2,3,4,5,6,7,8,9,10,15,20}中搜索选取。
实验环境为：Intel Core 2 2.40 GHz CPU，2.39 GHz、1.94 GB RAM，Windows XP SP3，MATLAB 7.1。
2.2 实验结果与分析为了利用源域知识弥补当前场景下信息过少造成受训系统泛化能力下降之缺陷，模拟数据集的构造需遵循以下原则：1)源域和目标域之间既有很大相似性，又存在区别；2)已知的目标域数据集(x,y)是精确的，但由于样本过少，不能构建出概率密度估计回归函数。
为了表征上述原则，首先生成样本数较多且能精确表示概率密度分布均值为0、方差为1的源域数据集，需指出的是文章1.2.2节说明无偏置 v-SVR 与CC-MEB等价且概率密度函数可由CC-MEB中心点组成，若源域有数据隐私保护的需要，还可通过核心集技术，求得源域数据集的核心集，由少量核心集元素表示源域CC-MEB的中心点，进行迁移学习。另一方面，为了表示目标域与源域相近但不同，目标域设置时对均值、方差进行漂移，分均值、方差、均值方差均漂移3种情况，如表 1所示。
| 数据源 | 均值 | 方差 |
| 源域 | 0 | 1 |
| 目标域(均值漂移) | 0.1 | 1 |
| 目标域(方差漂移) | 0 | 1.1 |
| 目标域(均值、方差漂移) | 0.1 | 1.1 |
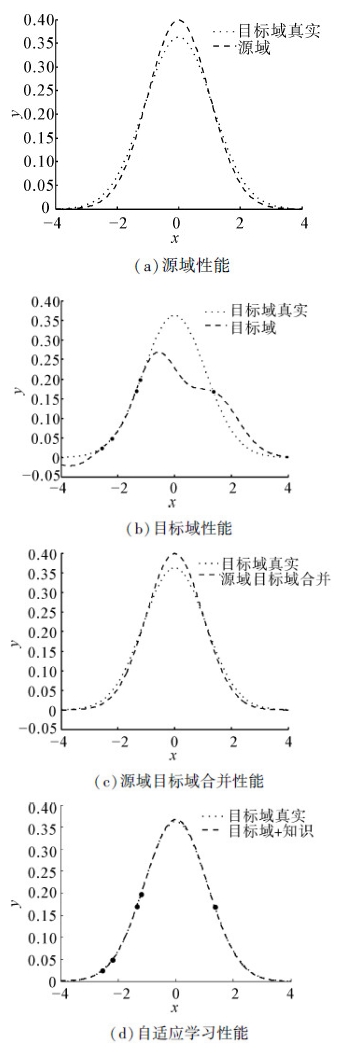
由于隐私保护等原因，目标域获得信息量少且精确，但不足以构建目标域概率密度函数。图 1(a)虚线显示了均值为0、方差为1.1时目标域真实概率密度分布图，图 1(b)显示了此种情况下目标域自适应学习效果图。图 2将本文所提算法与另外3种训练方法进行比较。
 |
| 图 1 均值为0、方差为1.1自适应学习效果图 Fig. 1 Charts of adaptive learning on the data set with mean 0,variance 1.1 |
 |
| 图 2 原始图像和退化仿真图像 Fig. 2 Performance comparison charts of different algorithms |
表 2列出了设置目标域不同均值方差后各算法的性能。
| 均值 | 方差 | 源域 密度估计性能 | 目标域 密度估计性能 | 源域+目标域 密度估计性能 | 源域知识+目标域 密度估计性能 | μ值 |
| 0 | 1.1 | 2.282 1×10-4 | 0.003 2 | 2.279 2×10-4 | 3.125 5×10-6 | 4 |
| 0 | 1.2 | 7.959 2×10-4 | 0.002 9 | 7.959 1×10-4 | 1.609 5×10-6 | 2 |
| 0.1 | 1 | 1.757 4×10-4 | 0.003 2 | 1.757 3×10-4 | 3.763 5×10-7 | 8 |
| 0.2 | 1 | 7.003 2×10-4 | 0.003 5 | 7.003 0×10-4 | 6.646 1×10-5 | 20 |
| 0.1 | 1.1 | 3.795 2×10-4 | 0.002 5 | 3.257 6×10-4 | 1.451 1×10-6 | 5 |
| 0.2 | 1.2 | 0.001 3 | 0.004 1 | 0.001 3 | 5.445 3×10-6 | 7 |
生成均值为0、方差为1源域样本10 000个，如图 1(a)所示，实线表示源域概率密度函数曲线，使用核心集技术获得源域的核心集由13个空心圆表示，源域知识只需知道模型参数和这13个样本点即可获得。虚线表示均值为0、方差为1.1的目标域真实概率密度函数曲线。由图 1(a)可以看出，源域、目标域分布近似但不相同。图 1(a)中5实点表示目标域已知信息，为了体现数据隐私保护的目的，文中实验选取的5个样本均在[-1, 1]之外。点划线表示由这5个点获得的目标域概率密度函数曲线。由图可知,虽然已知信息精确，但信息过少不能反映目标域真实概率密度分布。图 1(b)显示了不同μ值自适应学习效果图，随着μ值的增大，目标域概率密度曲线向目标域真实分布靠拢。此种自适应学习的优势在于，既可保证目标域已知信息精确表示，又可通过源域知识对未知信息进行自适应学习，极大提高目标域概率密度估计性能。
根据表 2和图 2，可给出如下的观察：
1) 从表 2可知，本文提出的DA-PDF算法充分利用目标域已知信息的同时，学习了源域知识，较之于两域各自训练、合并训练所得概率密度估计函数具有更好的性能。
2) 对图 2(a)可知，若直接使用源域概率密度估计函数对现有测试集进行密度估计，效果不理想，其原因在于目标域与源域密度分布已发生变化(源域方差为1，目标域方差为1.1)，这种变化导致若继续使用源域模型进行预测，其预测性能不好，无法达到与目标域实际情况逼近的效果。
3) 对图 2(b)可知，由于在当前场景下采集的数据数量较少，虽然这些数据真实可靠，但对于构建整个概率密度估计函数信息量过少，故密度估计性能低下。
4) 对图 2(c)可知，使用源域数据与目标域数据结合后生成的概率密度估计函数，其性能提升不明显。原因在于源域数据较之目标域收集到的数据，数据量大，因此在模型训练时，其所占的比重也大，故得到的概率密度估计函数最终更偏向于源域数据所得模型。合并训练另一缺点是需要源域所有数据参与模型的建立，但一些高度机密的历史数据通常难以获取，若源域有数据隐私保护的需要，此种方法则无法实现。
5) 从图 2(d)可知：本文方法较之图 2(a)有更好的逼近效果；与图 2(b)相比，可利用源域知识较好地弥补目标域信息不足的缺陷；与图 2(c)相比，不仅逼近程度有明显改进，且本文方法只需要历史知识(历史模型参数)以及目标域数据，并不需要源域数据作为训练数据，因而在隐私保护方面也体现了较大优势。
3 结束语本文采用无偏置v-SVR对已知概率密度(x,y)对进行概率密度函数建模，并证明无偏置v-SVR等价于CC-MEB且概率密度回归函数可由CC-MEB中心点表示，以此为前提，提出中心点领域自适应学习的概率密度估计函数建模思想，解决多领域相关联且某一领域信息较少无法构建概率密度函数的问题。本文所提方法不需要大量源域数据的支持，仅是继承历史知识(源域中心点)，且允许当前领域信息较少，不但能够根据历史知识进行当前领域的信息补偿，又能对源域数据进行隐私保护，这些特性是传统概率密度估计方法所不具备的。通过合成数据的仿真实验表明本文方法较之于传统方法具有更好的适应性。
| [1] | VAPNIK V N. Statistical learning theory [M]. New York:John Wiley and Sons, 1998: 35-41. |
| [2] | 吉根林, 姚瑶. 一种分布式隐私保护的密度聚类算法[J].智能系统学报, 2009, 4(2):137-141.JI Genlin, YAO Yao. Density-based privacy preserving distributed clustering algorihtm[J]. CAAI Transactions on Intelligent Systems, 2009, 4(2):137-141. |
| [3] | PARZEN E. On estimation of a probability density function and mode[J]. The Annals of Mathematical Statistics, 1962, 33(3): 1065-1076. |
| [4] | GIROLAMI M, HE C. Probability density estimation from optimally condensed data samples[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25 (10): 1253-1264. |
| [5] | DENG Z H, CHUNG F L, WANG S T. FRSDE: Fast reduced set density estimator using minimal enclosing ball approximation[J]. Pattern Recognition, 2008, 41(4):1363- 1372. |
| [6] | TSANG I W, KWOK J T, ZURADA J M. Generalized core vector machines[J]. IEEE Transactions on Neural Networks, 2006, 17(5): 1126-1140. |
| [7] | TSANG I W, KWOK J T, CHEUNG P M. Core vector machines: fast SVM training on very large data sets[J]. Journal of Machine Learning Research, 2005(6): 363-392. |
| [8] | CHU C S, TSANG I W, KWOK J K. Scaling up support vector data description by using core-sets[C]//IEEE International Joint Conference on Neural Networks. Budapest, Hungary: 2004: 425-430. |
| [9] | 许敏,王士同. 基于最小包含球的大数据集域自适应快速算法[J]. 模式识别与人工智能, 2013, 26(2): 159-168.XU Min, WANG Shitong. A fast learning algorithm based on minimum enclosing ball for large domain adaptation[J]. Pattern Recognition and Artificial Intelligence, 2013, 26(2): 159-168. |