2. 苏州大学 计算机信息处理技术省重点实验室, 江苏 苏州 215006
2. Provincial Key Laboratory for Computer Information Processing Technology, Soochow University, Suzhou 215006, China
特征选择是机器学习、模式识别、医疗诊断等领域的一个研究热点。特征选择是一种重要的数据处理方法,从很多输入特征集中选择一个重要特征的子集并且移除不相关或不重要的特征,使留下的特征具有更强的分辨率。本文研究重点是基于支持向量机(support vector machine,SVM)的特征选择方法,也就是把SVM引入到特征选择过程中。基于SVM的特征选择算法分为3类:基于SVM的Wrapper特征选择算法、基于SVM的Embedded特征选择算法和基于SVM的Filter与Wrapper的混合特征选择算法。Weston等提出的基于SVM的Wrapper特征选择算法是去寻找能最小化泛化误差边界的特征,这种寻找可以通过梯度下降来实现[1]。Guyon等提出的SVM-RFE(recursive feature elimination)是这种算法中最具代表性的一个[5]。针对传统SVM-RFE特征选择算法中SVM参数(软间隔参数 γ 和惩罚因子 C )难以确定的问题,王俭臣等[2]采用粒子群算法搜索SVM的参数,并且将特征向量映射到SVM参数 γ 确定的核空间中去进行特征选择,这样就有效地将特征选择与SVM分类器关联起来。但该方法由于采用序列向后搜索,具有较高的时间复杂度。Li等[3]提出的基于SVM的Embedded特征选择算法同时实现了分类与特征选择。该方法通过引入数据驱动权重,从而自适应地辨别出重要特征。此外,重要特征的系数偏差也大大减少。但是该方法有较多的参数设置,算法在很大程度上依赖于参数的调整。Lee等[4]提出了基于SVM的Filter与Wrapper的混合特征选择算法,并将其应用在微阵列数据分析中。此方法首先用动态参数设置的遗传算法产生大量的特征子集,然后根据特征子集中出现的频率来选择特征,最后选择一定数量的排序靠前的特征。
对平衡的数据集来说,采用SVM的方法来进行特征选择是非常合适的。但是当数据集本身具有不平衡性时,再采用SVM方法就不太合适了。针对这个问题,Jeong等[11]提出了2种基于支持向量数据描述(support vector data description,SVDD)的特征选择算法:SVDD-radius-RFE和SVDD-dual-objective-RFE。支持向量数据描述也称为1类SVM方法,这里沿用文献[11]的术语。SVDD-radius-RFE方法可以用来最小化描述正常样本的边界,这个边界通过半径的平方来衡量。SVDD-dual-objective-RFE方法可得到SVDD对偶空间的一个紧致描述,这个描述可通过最大化SVDD对偶目标函数得到。然而,这2种方法在样本维数较高时,时间复杂度会非常大。
为此,提出了一种新的基于支持向量数据描述的特征选择算法。在新的方法中,依据超球体球心向量上的方向能量大小来消除特征。若在某些方向上的能量较小,就会消除此方向所对应的特征。在基因数据集上的实验结果证明了新方法SVDD-RFE方法获得了更精确的分类性能和更少的时间消耗。
1 相关工作 1.1 支持向量数据描述(SVDD)SVDD是一种描述目标数据分布的方法,也称为1类SVM[6, 7, 8]。SVDD与SVM唯一的不同就是,仅允许从一类数据中去学习。SVDD有2种版本。一种是支持向量描述超平面的方法[7]。这种方法的线性版本是将原点视为异常点,使得最优超平面尽可能远离原点。另一种是Tax和Duin提出的超球面的SVDD方法[6, 8]。此外,Campbell和Bennett提出了基于线性规划的SVDD方法[9]。Zhang等[13]提出了一种改进的SVDD方法,适用于线性非圆数据描述的情况。在文献[10]中,Zhang等将数据描述方法引入到了隐空间,这是一种广义的非线性数据描述方法。
这里,简要介绍基于超球体的SVDD方法[6, 8]。SVDD仅需要一类数据或目标数据来构建由超球体表示的学习模型。若一个点落在超球体内,则这个点就属于目标数据集。若落在超球体外,则这个点就是异常点。给定一个目标样本 {xi}i=1n ,其中 xi∈RD 是目标样本,D 是目标样本的维数,n 是目标样本的个数。试图找到一个具有最小体积并能包含所有(或大多数)数据的超球体。为了得到这个超球体,需知道2个参数,即超球体的球心 a 和半径 R 。SVDD需要求解下述对偶规划来得到这2个参数:
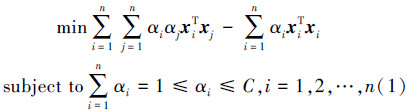
超球体的球心 a 可以用拉格朗日乘子表示为

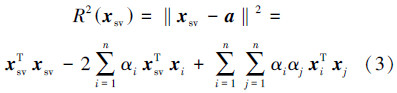
这里简单地介绍一下已有的基于SVDD的特征选择方法,即SVDD-radius-RFE和SVDD-dual-objective-RFE特征选择方法[11]。
1.2.1 SVDD-radius-RFE在文献[11]中,对SVDD-radius-RFE的规划给出了2种情况:没有可用的异常数据和少量可用的异常数据。本文中,仅针对没有可用的异常数据进行讨论。
令训练样本有 n 个,边界半径的平方如式(3)所示。用所有支持向量获得的 R2(xsv )的平均值作为衡量边界大小的准则函数,则该平均值 Jr 定义为
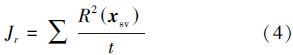
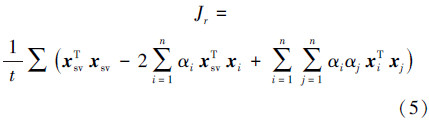
令 Jr(-P) 为除特征 P 以外获得的球半径。则最坏的特征是具有最大 Jr(-P )值所对应的特征。移除特征 P 后,准则函数的有效性可用 DJr(P)=Jr-Jr(-P) 来表示。最坏的特征是具有最小值的 DJr(P) 对应的特征。
1.2.2 SVDD-dual-objective-RFE令 Jd 和 Jd(-P) 分别为SVDD对偶规划中对偶函数的值和移除特征 P 后对偶规划的值。 Jd 是式(1)中对偶规划具有相似的值,即:
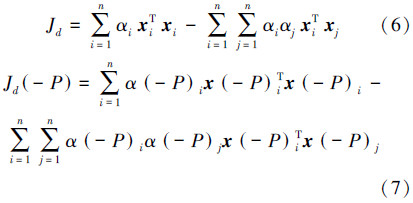
用 DJd(P)=Jd-Jd(-P) 作为衡量准则函数来消除冗余特征,最坏的特征 P* 是在所有特征中,具有最小 Jd(-P) 值的那一个。即
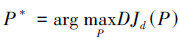
本节提出了一种新的基于支持向量数据描述的特征选择算法,即SVDD-RFE。
SVM特征选择是利用权向量 w 来进行特征消除。SVDD不存在权向量 w ,但具有超球体的中心 a=[a1 a2 … aD]T 。 |ai| 的值表示目标样本的第 i 个方向的平均幅值。则 ai2 表示第 i 个方向的能量。第 i 个方向上的能量越大,则目标样本在第 i 个方向上的分布就越广。若能量在第 i 个方向上较小,则数据在该方向上必然非常紧凑。注意到作者的目的是让尽可能多的目标数据包含在超球体内。紧凑的数据将形成一个小半径的超球体,这样的超球体可能不会包含大部分的数据。因此,紧凑分布方向的特征应该被移除,同时分布较散的方向应该保留。
因而,用 ai2 表示第 i 个特征的重要性。那么就可以根据能量 ai2来消除不重要特征。SVDD-RFE从特征集合中迭代消除特征,这个迭代过程分以下3步完成。1)由目标数据训练SVDD,得到超球体的中心;2)计算所有特征的 ai2,i=1,2,…,D ;3)从原始特征集移除具有最小 ai2值所对应的特征。重复这个迭代过程直到满足终止条件。具体算法在下面的算法1中给出。
注意算法1中的 F 是已选特征的索引集合,也意味着这些特征已保留下来。本算法旨在特征的选择和得到较少特征的数据集合。对于最后得到的数据集,任何分类器,都可以用来建立分类模型。
算法1 SVDD-RFE
输入: 训练样本 {xi}i=1n ,其中 xi∈RD ,n 是训练样本的个数,D 是样本维数,子空间维数用 d 表示;
输出: 被选择特征的索引集合 F 。
1)初始化被选特征的索引集合 F={1,2,…,D} 并且令 m=D 。
2)求解对偶规划(1),得到超球体的中心 a=[a1 a2 … am]T∈Rm 。
3)计算所有方向的能量 ai2 ,i=1,2,…,m 。
4)找到具有最小能量的特征 。
。
5)令 m=m-1 ,令被选特征索引集合 F=F\P,并从训练样本集合中消除第 P 个特征,得到更新的训练样本集合 {xi}i=1n ,其中 xi∈Rm 。
6)若 m=d ,算法结束;否则转到2)。
3 实验结果在DNA微阵列的基因表达数据集上进行实验,要验证SVDD-RFE算法的正确性和有效性。实验数据集是Leukemia数据集。在Leukemia数据集中,有2种不同种类的白血病,急性淋巴细胞性白血病(acute lymphoblastic leukemia,ALL) 和急性骨髓性白血病(acute myeloid leukemia,AML)。
数据集被划分为2个子集:训练集和测试集。训练集用来选择基因和调整分类器权重,测试集用来估计分类性能。训练集有38个样本(27个ALL和11个AML),测试集有34个样本(20个ALL和14个AML)。所有样本有7 129个特征,对应于从微阵列图像中提取出的归一化基因表达值。本实验中,将ALL视为目标样本,AML视为负类样本。本数据集可从文献[12]中得到。本实验中的所有方法是从7 129个特征中选取100个重要特征,并且仅有参数 C 需要设置。接下来的实验中,将会讨论已选特征的好坏,然后去衡量分类精度的性能。
本实验的对比方法有SVM-RFE、SVDD-radius-RFE、SVDD-dual-objective- RFE以及SVDD-RFE。用KNN(nearest neighbor)分类器来衡量选择的特征是否合适。KNN由于其简单性和有效性成为一种很方便的分类器,它的核心思想是在训练集合中找到距离测试样本点最近的 k 个点,然后将该测试样本点的类别设置为 k 个点中数量最多类的类别标签。
因为选择KNN作为分类器,参数 k 的选择对分类精度有一定影响。出于运行时间上的考虑,仅对SVM-RFE和SVDD-RFE做了参数 k 的比较。令 k 从1~10变化,同时分别令SVM-RFE中 C=100 ,在SVDD-RFE 中 C=0.1 。图 1给出了2种算法在不同 k 值下的分类精度变化曲线。
 |
| 图 1 分类精度的变化 Fig. 1 The accuracy with the change |
从图 1可以看出,SVDD-RFE相较于SVM-RFE可以得到更好的分类精度。且在 k=6 时达到最好。但通常会选择奇数,因此接下来的实验中,选择 k=5 。接下来研究参数 C 的变化对4种特征选择方法性能的影响。对于SVM-RFE,C 在 {0.1,1,10,100,1000} 集合中取值,对于SVDD-RFE、SVDD-radius-RFE和SVDD- dual-objective-RFE 3种方法,C 在 [1/n,1] 中取5个线性等距间隔,n 是训练样本的个数,即 {0.037,0.28,0.52,0.76,1} 。在表 1中,给出了不同 C 变化下,各种方法的分类召回率。此外还有不进行特征选择时,直接采用KNN分类器的识别效果。
| SVM-RFE | SVDD-radius-RFE | ||||||||
| C 值 | ALL的召 回率/% | AML的 召回率/% | 平均召 回率/% | 运行时 间/s | C 值 | ALL的召 回率/% | AML的 召回率/% | 平均召 回率/% | 运行时 间/s |
| 0.1 | 100.00 | 14.29 | 57.14 | 507.64 | 0.037 | 0 | 100.00 | 50.00 | 154 058.76 |
| 1 | 100.00 | 14.29 | 57.14 | 491.95 | 0.28 | 100.00 | 35.71 | 67.86 | 11 917.37 |
| 10 | 100.00 | 14.29 | 57.14 | 500.43 | 0.52 | 100.00 | 42.86 | 71.43 | 12 432.45 |
| 100 | 100.00 | 14.29 | 57.14 | 432.83 | 0.76 | 100.00 | 42.86 | 71.43 | 11 575.10 |
| 1000 | 100.00 | 14.29 | 57.14 | 431.20 | 1 | 100.00 | 42.86 | 71.43 | 10 359.75 |
| SVDD-dual-objective-RFE | SVDD-RFE | ||||||||
| C 值 | ALL的召 回率/% | AML的 召回率/% | 平均召 回率/% | 运行时 间/s | C 值 | ALL的召 回率/% | AML的召 回率/% | 平均召 回率/% | 运行时 间/s |
| 0.037 | 100.00 | 21.43 | 60.71 | 44 230.98 | 0.037 | 95.00 | 92.86 | 93.93 | 163.87 |
| 0.28 | 95.00 | 35.71 | 65.36 | 9 522.17 | 0.28 | 100.00 | 50.00 | 75.00 | 137.82 |
| 0.52 | 100.00 | 7.14 | 53.57 | 9 721.61 | 0.52 | 100.00 | 50.00 | 75.00 | 165.13 |
| 0.76 | 100.00 | 7.14 | 53.57 | 10 253.75 | 0.76 | 100.00 | 50.00 | 75.00 | 155.48 |
| 1 | 100.00 | 7.14 | 53.57 | 9 398.531 | 100.00 | 50.00 | 75.00 | 153.83 | |
| None | |||||||||
| C 值 | ALL的召 回率/% | AML的 召回率/% | 平均召 回率/% | 运行时 间/s | |||||
| - | 100.00 | 29.00 | 64.50 | - | |||||
从表 1中可以看出,文中提出的方法得到了最好的平均召回率,另外,表中也给出了几种方法的运行时间,运行时间是指特征选择的时间。很明显,SVDD-RFE选择了更好的特征来区分ALL和AML,同时在时间消耗方面比其他3种方法都要少很多,尤其是与SVDD-radius-RFE和SVDD-dual-objective- RFE方法相比。
分别令 C=0.037 (SVDD-RFE),C=100 (SVM-RFE),C=1 (SVDD-radius-RFE和SVDD-dual-objective-RFE),图 2(a)和(b)给出了2种方法(SVDD-RFE和SVM-RFE)选择的100个特征的能量或权重,未选特征的能量或权重置为0。图 2(c)和(d)给出了另外2种方法(SVDD-radius-RFE和SVDD-dual-objective-RFE)移除特征 P 后DJr (P) 和DJd(P)的值。
 |
| 图 2 原始图像和退化仿真图像 Fig. 2 Original image and simulated degraded image |
文中提出了一种新的基于支持向量数据描述的特征选择算法,并且将其用于癌症分类。该算法可以轻松处理小样本、多特征的分类问题,也可以在消除特征冗余的同时实现特征选择。更重要的是,该算法不仅得到了更为紧凑、更具有分辨能力的基因子集,还具有更好的稳定性和有效性。在Leukemia数据集上的实验验证了算法的正确性。实验中,用KNN分类器来衡量特征选择的性能。在Leukemia数据集上,SVDD-RFE方法选择的特征集合不仅具有最好的分辨力,时间消耗也最少。未来工作中,将运用SVDD的特征选择,进一步提高分类率。
| [1] | WESTON J, MUKHERJEE S, CHAPELLE O, et al. Feature selection for SVMs[C]//Proc of Neural Information Processing Systems. Denver, USA: 2000: 668-674. |
| [2] | 王俭臣, 单甘霖, 张岐龙, 等. 基于改进 SVM-RFE 的特征选择方法研究[J]. 微计算机应用, 2011, 32(2): 70-74.WANG Jianchen, SHAN Ganlin, ZHANG Qilong,et al. Research on feature selection method based on improved SVM -RFE[J]. Microcomputer Applications, 2011, 32(2): 70-74. |
| [3] | LI Juntao, JIA Yingmin, LI Wenlin. Adaptive huberized support vector machine and its application to microarray classification[J]. Neural Computing and Applications, 2011, 20(1): 123-132. |
| [4] | LEE C, LEU Y. A novel hybrid feature selection method for microarray data analysis[J]. Applied Soft Computing, 2011, 11(1): 208-213. |
| [5] | GUYON I, WESTON J, BARNHILL S, et al. Gene selection for cancer classification using support vector machines[J]. Machine Learning, 2002, 46(1/2/3): 389-422. |
| [6] | TAX D M J, ROBERT PW D. Support vector domain description[J]. Pattern Recognition Letters, 1999, 20(11): 1191-1199. |
| [7] | SCHIILKOPP B, BURGEST C, VAPNIK V. Extracting support data for a given task[C]//Proceedings of First International Conference on Know ledge Discovery and Data mining.1995: 262-267. |
| [8] | TAX D M J, DUIN R P W. Data domain description using support vectors[C]//ESANN. Facto, Brussels, 1999: 251-256. |
| [9] | BENNETT C C K P. A linear programming approach to novelty detection[C]//Advances in Neural Information Processing Systems 13: Proceedings of the 2000 Conference. Boston: MIT Press, 2001, 13: 395-401. |
| [10] | ZHANG Li, WANG Bangjun, LI Fanzhang, et al. Support vector novelty detection in hidden space[J]. Journal of Computational Information Systems, 2011(7): 1-7. |
| [11] | JEONG Y S, KONG I H, JEONG M K, et al. A new feature selection method for one-class classification problems[J]. Systems, Man, and Cybernetics, Part C: Applications and Reviews, 2012, 42(6): 1500-1509. |
| [12] | ARMSTRONG S A, STAUNTON J E, SILVERMAN L B, et al. MLL translocations specify a distinct gene expression profile that distinguishes a unique leukemia[J]. Nature Genetics, 2002, 30(1): 41-47. |
| [13] | ZHANG Li, ZHOU Weida, LIN Yin, et al. Support vector novelty detection with dot product kernels for non-spherical data[C]//Proceedings of the 2008 IEEE International Conference on Information and Automation. Zhangjiajie, China, 2008: 41-46. |



