生物发酵过程是一个具有高度非线性与不确定性和兼有生物、化学、物理和热力变化的复杂生化反应过程。一些反映发酵过程品质的重要参量,如菌体浓度、基质浓度、产物浓度等,目前还缺乏在线测量的仪器与手段,影响了在线优化控制的实施。对于这些重要过程参量的测量,目前主要采取在线取样、离线分析的方法,但这种方法时间间隔长、数据滞后大,难以满足生物反应过程在线控制的要求,同时在线取样容易造成反应过程菌体污染,降低反应过程的质量。为了解决这一难题,人们提出软测量的理论与方法。
软测量技术起源于20世纪70年代Brosillow提出的推断控制思想[1],其基本原理是构造以直接可测的辅助变量为输入的数学模型来估计难以直接测量的主导变量。软测量建模方法可分为机理建模、数据驱动建模、混合建模3种,其中数据驱动建模是从大量过程数据中提取过程信息从而建立软测量模型,不需要获得对象过程的精确数学模型,它尤其适用于生物反应过程这一类内部机理尚不明确的复杂过程。数据驱动建模主要有神经网络、支持向量机、高斯过程回归(GPR)等方法,其中高斯过程回归将高斯先验分布运用于非参数回归函数空间,通过推导预测目标的后验分布建立统计模型,高斯过程回归可以同时获得预测输出与预测精度,显著提高软测量模型的性能。与神经网络、支持向量机等回归方法相比,高斯过程回归具有优化参数少、收敛速度快、模型精度高、泛化能力强等优点,在实际生物发酵工业中具有较好的应用效果[2,3,4,5,6]。
文中给出一种生物反应过程关键参量的基于模糊C均值聚类(FCM)与集成高斯过程回归建模方法。针对生物发酵过程可分为延滞期、指数生长期、稳定期、死亡期4个反应周期的特点,采用模糊C均值聚类方法将过程数据样本分成4个子类,分别对每个子样本集采用高斯过程回归训练,训练过程采用Adaboost算法以进一步提高软测量模型的泛化能力。对于新样本,通过计算样本点到各聚类中心的距离确定新样本点对每个GPR模型的隶属度,通过加权综合给出软测量模型的预测输出。针对氨基酸类典型菌种L-赖氨酸反应过程的菌体浓度参量,建立软测量模型并开展相关的仿真实验研究。仿真结果表明,与单一高斯过程模型、集成GPR模型和基于FCM与多GPR模型方法相比,基于FCM与集成GPR的软测量模型具有更好地逼近精度与泛化能力,较好地满足了赖氨酸发酵过程软测量的要求。
1 高斯过程及其回归算法 1.1 高斯过程原理高斯过程(GP)是在高斯随机过程与贝叶斯学习理论基础上发展起来的一种新型机器学习方法,它描述了一类随机过程:其任意有限变量集合的分布都是高斯过程,即对任意整数n≥1及任意一族随机变量X,与其对应的t时刻过程状态f(X)的联合概率分布服从n维高斯分布。GP的全部统计特征完全由其均值m(t)与协方差函数k(t,t')确定,定义表示如下:
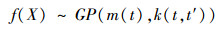
给定样本训练集D={(xi,yi)|i=1,2,…,n},其中xi∈Rd是d维输入向量,yi∈R是相应的输出量。为了符号描述方便,用X表示输入向量构成的d×n维输入矩阵,y表示输出标量构成的输入矢量,那么训练集可表示为D=(X,y)。对于新样本x*,GP模型根据先验知识预测与x*相对应的输出值y*。
假设观察目标值y被噪声腐蚀,它与真实输出值t相差ε,即

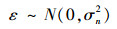
观测目标值y的先验分布为
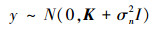
由此,n个训练样本输出y和1个新样本输出y*构成的联合高斯先验分布为
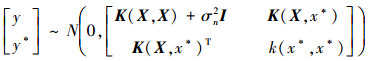
GP的协方差函数需要满足对任一点集都能够保证产生一个非负正定协方差矩阵。常用的协方差函数为
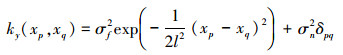

对于新的输入样本x*,根据贝叶斯原理可以获得对应的预测值y*,其预测分布是高斯型:
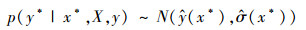
 和方差
和方差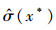 分别为
分别为

FCM算法[7,8,9,10,11]是由Dunn提出,经由Bezdek应用发展起来的一种模糊聚类算法,其原理是通过最小化基于范数与聚类原型的目标函数将无标签的数据进行分类。对于给定的样本集合X={x1,x2,…,xn}⊂Rs,其中s是样本空间的维数,n是样本个数,令c(c>1)是对X进行划分的聚类个数,则FCM算法的优化目标为



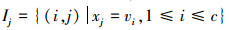 ,若Ij=∅,则:
,若Ij=∅,则:
 ,i=1,2,…,c;j=1,2,…,n
,i=1,2,…,c;j=1,2,…,n
若Ij≠∅,则uij是满足如下条件的任意非负实数:
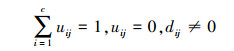
关于隶属度的迭代公式是一个从点到集合的映射,在实际计算中通常采用如下的隶属度更新公式:
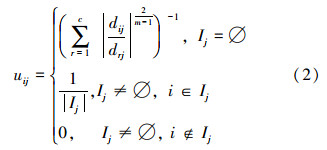
FCM算法先初始化类中心或隶属度矩阵,然后利用式(1)和式(2)进行迭代直至满足设定的终止条件,其具体实现步骤如下:
1)设定聚类个数c和模糊指数m;初始化类中心V(0);设置收敛精度ε>0;令迭代次数k=0。
2)利用式(2)计算U(k+1)。
3)利用式(1)计算V(k+1),令k=k+1。
4)重复2)和3),直到满足如下的终止条件:

Adaboost (Adaptive boost)算法[12,13,14]是Boosting算法的一种,这种思想源于Valiant提出的PAC[15](probably approximately correct)学习模型。其主要内容是获取各学习样本的权重分布,所有权重被赋予相等的初始数值,但在训练过程中,这些样本权重被不断调整,预测精度低的样本权重得到加强,预测精度高的样本权重则被减弱。最终,弱预测器加强了对难以预测的样本的学习。这样以后,达到一定预测精度的弱预测器,经组合后形成的强预测器就具有很高的预测精度。文中利用此算法对高斯过程回归模型的学习能力进行提升,以提高模型的泛化能力和预测性能。
4 基于FCM与集成GPR的软测量模型构建这里以氨基酸类典型菌种L-赖氨酸反应过程的菌体浓度软测量为例,阐述基于FCM与集成GPR的软测量模型构建步骤。考虑到赖氨酸反应过程中微生物生长可分为延滞期、指数生长期、稳定期和死亡期4个阶段,将预处理后的样本集依据FCM算法分成4个子类,即c=4,根据经验取m=2[16],然后采用基于Adaboost算法的集成GPR方法对每个子集建立软测量模型。具体建模步骤为
1) 根据赖氨酸反应实验过程的实测值建立训练样本(xi,yi),i=1,2,…,k,其中xi∈Rd是d维输入矢量,表示反应过程中影响菌体浓度的主要因素;相应的输出标量yi∈R,为菌体浓度值。
2) 为进一步提高建模精度,对所有数据进行噪声滤波和归一化预处理,得到样本矩阵 。
。
3) 构造模糊关系矩阵R=(riq),其中riq为描述样本i和q之间相似程度的系数,采用欧式距离表示:
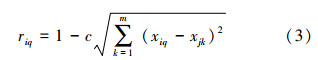
4) 计算模糊关系等价矩阵R'。利用平方法对模糊关系矩阵R进行2,4,…,2k幂次计算,直到R2k=R2k-1,则得到R'=R2k。
5) 在模糊关系等价矩阵R'中,根据设定的分类数c=4,采用λ-截距阵法得到样本的初始聚类,然后,以各子类平均值为初始聚类中心,记为V1(0),V2(0),V3(0)和V4(0)。
6) 用式(3)计算样本与初始聚类中心的近似程度。
7) 计算归一化后的样本矩阵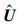 的隶属度矩阵U(0)。U(0)=(uij(0)),
的隶属度矩阵U(0)。U(0)=(uij(0)),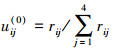 。
。
8) 利用FCM聚类算法进行迭代,直至达到收敛精度。
9) 样本聚类完成后,针对每个子类的样本数据分别训练子模型,结构如图 1所示。
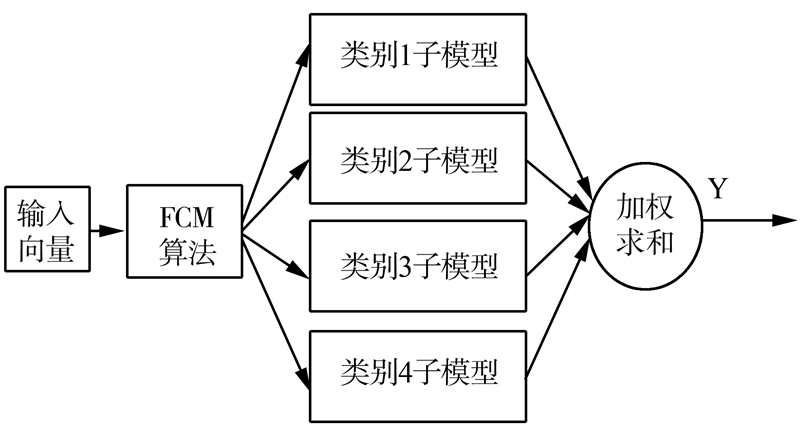 |
| 图 1 基于FCM与多集成GPR软测量模型结构Fig. 1 Model structure of multiple integrated GPR based on FCM |
10) 针对训练子模型,采用基于Adaboost算法的集成高斯过程回归模型,给定子学习样本为(x1,y1),…,(xp,yp),xu∈xi,yu∈yi,u=1,2,…,p从子类的样本空间中随机选择d组训练数据,初始化测试数据的分布权值Dt(u)=1/d、GPR模型的最大迭代次数t=1,2,…,T。
11) 利用样本权重Dt训练弱GPR学习器。
12) 获取弱GPR学习器的预测函数ht:X→Y,并用εt=Pru-Dt[ht(xu)≠yu]用来表示对应的预测误差。
13) 选取 ,更新样本权重:
,更新样本权重:
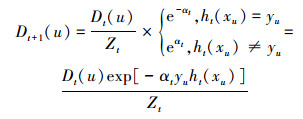
 。
。
14) 输出最终的预测函数为
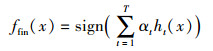
 |
| 图 2 基于Adaboost的GPR软测量模型结构Fig. 2 Model structure of GPR based on Adaboost |
15) 确定输入数据对于每个子模型的隶属度ui,根据隶属度将每个子模型的输出为ffin(x),最后得到赖氨酸发酵过程的菌体浓度预测值Y为

实验采用WKT-30L型液态发酵装备及其控制系统。根据赖氨酸发酵过程的工艺要求,发酵过程中的罐压保持在0.11 MPa,温度控制在31℃,搅拌电机转速为330 r/min。根据前期对赖氨酸反应过程的机理和数据分析[17,18,19,20],赖氨酸反应过程的菌体浓度值与溶解氧值、发酵液pH值、空气流等参量紧密相关。因此,本实验选取发酵液pH值、溶解氧Do与空气流量F3个参量作为辅助变量;关键生物参量菌体浓度Y作为主导变量,则赖氨酸发酵过程中菌体浓度软测量模型可描述为
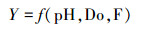
每批次反应周期为72 h,采样周期为15 min,通过测试仪器对发酵液pH值、溶解氧值、空气流量参量进行实时采集,每2 min取样并离线化验得到菌体浓度。菌体浓度采用细胞干重法计算得到,即取10 mL发酵液于离心管中,在3 000 r·min-1下离心5 min,弃上清,蒸馏水洗涤2次,在105℃干燥至恒质量后称量。
考虑5个批次培养数据以检验赖氨酸反应过程的基于FCM与集成GPR软测量模型。为增强各批次间的差异性,每批次间初始条件不同,补料策略亦有相应变化。采用WKT-30 L自动控制系统,将发酵罐温度控制在(0~50±0.5)℃。获得批次数据的前4批次作为训练样本集,离线训练获得基于FCM与集成GPR软测量模型,第5个批次用于测试样本集,检验基于FCM与集成GPR软测量模型的泛化能力。
数据样本的3D聚类效果如图 3所示,训练样本集被分成4类,分别用4个椭圆标记。目标函数值的变化曲线如图 4所示。结果分析可知,整体分类经过44次迭代,达到预设收敛精度,得到最终的目标函数值。
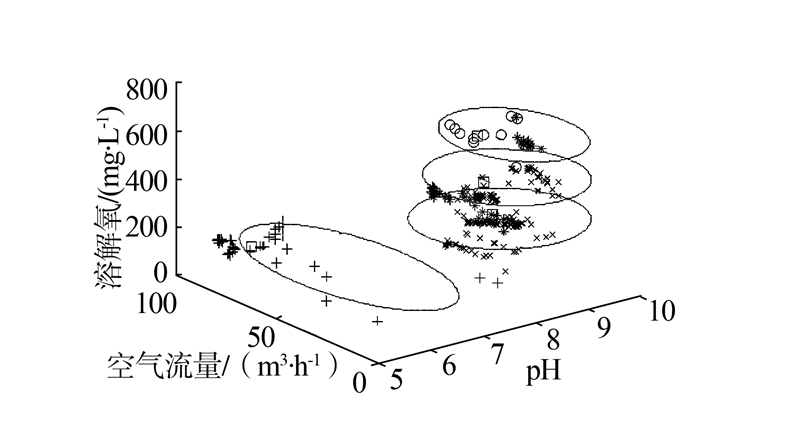 |
| 图 3 样本的3D聚类结果Fig. 3 3D cluster results in training set |
 |
| 图 4 目标函数值变化曲线Fig. 4 Variation curves of the objective function value |
基于FCM与集成GPR的软测量算法是在GPstuff-4.1基础上用MATLAB语言编写。为了验证该种方法的性能,将其与传统的单一GPR、集成GPR软测量模型和基于FCM与多GPR软测量模型相比,其中选取菌体浓度参量为预测目标,样本数据经过FCM聚类以后,分别建立采用Adaboost算法的集成GPR子模型,式中:设定算法的最大迭代次数t为10,初始误差为εt=0,针对测试样本集检验软测量模型的泛化能力。图 5所示为基于FCM与集成GPR软测量模型的预测值与样本真实值。
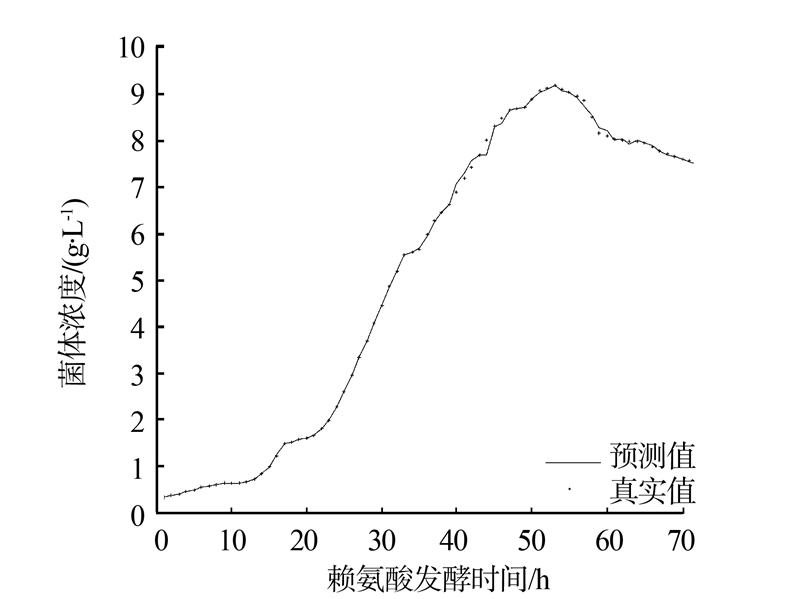 |
| 图 5 基于FCM-Adaboost-GPR的软测量模型预测值与真实值Fig. 5 Comparison between the predictive value and true value using integrated GPR soft sensor model based on FCM |
图 6显示了弱高斯过程回归模型(传统的单一高斯过程回归模型)与强高斯过程回归模型(集成高斯过程回归模型)针对测试样本集的泛化能力,经过Adaboost算法,弱高斯过程回归模型提升为强高斯过程回归模型,误差明显减小,泛化能力也大幅度提高。
 |
| 图 6 强GPR预测器与弱GPR预测器的预测值与真实值Fig. 6 Comparison between the predictive value and true value using strong GPR predictor and weak GPR predictor |
为了与其他软测量方法作对比研究,同时建立基于FCM与多GPR模型和单一GPR模型,模型对测试样本集的预测效果如图 7所示。单一GPR模型的预测输出误差大,基于FCM与多GPR模型的预测输出误差比单一GPR模型的预测输出误差小。
 |
| 图 7 多GPR和单一GPR软测量模型预测值与真实值Fig. 7 Comparison between the predictive value and true value using multiple GPR soft sensor model based on FCM and single GPR soft sensor model |
通过图 5~7仿真结果对比发现,基于FCM与集成GPR模型输出的预测值误差较小,预测精度高且较为平滑。
基于FCM与集成GPR软测量模型、集成GPR软测量模型、单一GPR软测量模型和多GPR软测量模型的相对误差对比如图 8所示。分析表明,多GPR软测量模型、集成GPR模型和基于FCM与集成GPR软测量模型总体上相对误差比较小,单一GPR软测量模型的相对误差则比较大,同时基于FCM与集成GPR模型误差明显小于集成GPR模型和多GPR模型。
 |
| 图 8 多GPR软测量模型、基于Adaboost-GPR软测量模型、单一GPR软测量模型和FCM-Adaboost-GPR软测量模型的相对误差Fig. 8 Comparison of relative error between multiple GPR soft sensor model based on FCM , GPR soft sensor model based on Adaboost ,single GPR soft sensor model and integrated GPR soft sensor model based on FCM. |
为了进一步比较分析4种模型的预测效果,分别定义平均相对误差σARE、均方根误差σRMSE与最大绝对误差σMAXE如下:
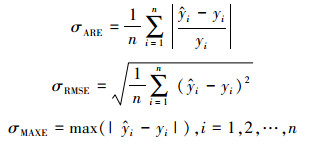
 为预测结果;yi为真实值。
为预测结果;yi为真实值。
ARE用来表示回归值符合真实值的平均程度,RMSE用来表示回归值和真实值的均方差大小,MAXE用来表示回归值偏离真实值的最大幅度。这3个性能指标参数的值越小,回归估计的效果就越好。表 1所示为4种模型分别对应的3种误差值,误差值表明,基于FCM与集成GPR的软测量模型预测效果优于单一GPR软测量模型、集成GPR软测量模型和多GPR软测量模型。对于3个性能指标,基于FCM与集成GPR的软测量模型比单一GPR软测量模型、集成GPR软测量模型和多GPR软测量模型都要小,由此可见,基于FCM与集成GPR软测量模型预测精度更高,泛化能力更好。
| 模型 | ARE | RMSE/g·L-1 | MAXE/g·L-1 |
| GPR | 0.076 7 | 0.020 8 | 0.721 8 |
| FCM-GPR | 0.036 5 | 0.009 5 | 0.404 9 |
| Adaboost-GPR | 0.015 1 | 0.012 1 | 0.484 2 |
| FCM-Adaboost-GPR | 0.005 1 | 0.006 7 | 0.310 8 |
针对氨基酸类典型菌种L-赖氨酸发酵过程中菌体浓度参量难以在线测量的难题,提出一种基于FCM与集成GPR的生物发酵关键参量软测量方法,该方法既有效克服了全局建模模型方法学习时间长,过程特性匹配不佳、预测精度低、外推和自适应能力差等缺点,又利用了Adaboost算法提升了高斯过程回归机的学习能力,增强了泛化能力。仿真结果表明,与多GPR软测量模型、集成GPR软测量模型和单一GPR软测量相比,基于FCM与集成GPR软测量模型具有较高的测量精度和较强的泛化能力,可应用于赖氨酸发酵过程菌体浓度关键参量的在线估计。
| [1] | BROSILLOW C B.Inferential control of process[J].Automatica,1978,24(3):485-509. |
| [2] | RASMUSSEN C E,WILLIAMS C K.Gaussian processes for machine learning[M].Boston:MIT Press,2006:7-31. |
| [3] | KOCIJAN J.Control algorithms based on Gaussian process models:a state-of-the-art survey[C]//Proc of the Special International Conference on Complex Systems:Synergy of Control,Communications and Computing.Ohrid,2011:69-80. |
| [4] | PETELIN D,KOCIJAN J,GRANCHAROVA A.Online Gaussian process model for the prediction of the ozone concentration in the air[J].Comptes Rendus del Academie Bulgare des Sciences,2011,64(1):117-124. |
| [5] | HE Z K,LIU G B,ZHAO X J,et al.Temperature model for FOG zero-bias using Gaussian process regression[J].Advances in Intelligent Systems and Computing,2012,180:37-45. |
| [6] | 孙斌,姚海涛,刘婷.基于高斯过程回归的短期风速预测[J].中国电机工程学报,2012,32(29):104-108.SUN Bin,YAO Haitao,LIU Ting.Short-term wind speed forecasting based on gaussian process regression[J].Proceedings of the CSEE,2012,32(29):104-108. |
| [7] | BEZDEK J C.Pattern recognition with fuzzy objective function algorithms[M].New York:Plenum Press,1981:15-28. |
| [8] | 曲福恒,胡雅婷,马驷良,等.基于核的模糊C均值聚类算法的收敛性定理[J].吉林大学学报:理学版,2011,49(6):1079-1086.QU Fuheng,HU Yating,MA Siliang,et al.A convergence theorem of kernel based fuzzyC-means clustering algorithm[J].Journal of Jilin University:Science Edition,2011,49(6):1079-1086. |
| [9] | MOHAMMAD T K,MOHAMMAD H B.A powerful hybrid clustering method based on modified stem cells and fuzzy C-means algorithms[J].Engineering Applications of Artificial Intelligence,2013,26,1493-1502. |
| [10] | XIAO Fengyin,LI P K,YIH T C.A fuzzy C-means based hybrid evolutionary approach to the clusering of supply chain[J].Computers&Industrial Engineering,2013,66(4):768-780. |
| [11] | BENAICHOUCHE A N,OULHADJ H,SIARRY P.Improved spatial fuzzy C-means clustering for image segmentation using PSO initialization,Mahalanobis distance and post-segmentation correction[J].Digital Signal Processing,2013,23(5):1390-1400. |
| [12] | PENG X J,SETLUR S,GOVINDARAJU V,et al.Using a boosted tree classifier for text segmentation in hand-annotated documents[J].Pattern Recognition Letters,2012,33(7):943-950. |
| [13] | 曹莹,苗启广,刘家辰,等.Adaboost算法研究进展与展望[J].自动化学报,2013,39(6):745-758.CAO Ying,MIAO Qiguang,LIU Jiachen,et al.Advance and Prospects of AdaBoost Algorithm[J].Acta Automatica Sinica,2013,39(6):745-758. |
| [14] | CHENG Wenchang,DING M J.A self-constructing cascade classifier with AdaBoost and SVM for pedestrian detection[J].Engineering Applications of Artificial Intelligence,2013,26(3):1016-1028. |
| [15] | VALIANT L G.A theory of the learnable[J].Communications of the ACM,1984,27(11):1134-1142. |
| [16] | 仲蔚,俞金寿.基于模糊C均值聚类的多模型软测量[J].华东理工大学学报,2000,26(1):83-87.ZHONG Wei,YU Jinshou.Study on soft sensing modeling via FCM based multiple models[J].Journal of East China University of Science and Technology,2000,26(1):83-87. |
| [17] | 黄永红,孙玉坤,王博,等.赖氨酸发酵过程关键参数的模糊神经网络逆软测量研究[J].仪器仪表学报,2010,31(4):862-867.HUANG Yonghong,SUN Yukun,WANG Bo,et al.Research of soft sensor based on fuzzy neural network inverse system for lysine fermentation process[J].Chinese Journal of Scientific Instrument,2010,31(4):862-867. |
| [18] | 王博,孙玉坤,嵇小辅.基于PSO-SVM逆的赖氨酸发酵过程软测量[J].化工学报,2012,63(9):3000-3007.WANG Bo,SUN Yukun,Ji Xiaofu,et al.Soft-sensor modeling for lysine fermentation processes based on PSO-SVM inversion[J].CIESC Journal,2012,63(9):3000-3007. |
| [19] | 孙玉坤,王博,黄永红.基于聚类动态LS-SVM的L-赖氨酸发酵过程软测量方法[J].仪器仪表学报,2010,31(2):404-409.SUN Yukun,WANG Bo,HUANG Yonghong,et al.Soft-sensing method for L-lysine fermentation process based on FDLS-SVM[J].Chinese Journal of Scientific Instrument,2010,31(2):404-409. |
| [20] | 黄丽,孙玉坤,嵇小辅,等.基于tPSO-BPNN的赖氨酸发酵软测量[J].仪器仪表学报,2010,31(10):2317-2321.HUANG Li,SUN Yukun,JI Xiaofu,et al.Soft sensor of lysine fermentation based on tPSO-BPNN[J].Chinese Journal of Scientific Instrument,2010,31(10):2317-2321. |



