2. 西安理工大学 自动化与信息工程学院, 陕西 西安 710000
2. Automation and Information Engineering College, Xi'an University of Technology, Xi'an, 710000, China
压缩感知理论的突出优点在于能够同时完成信号获取和压缩,它突破了奈奎斯特采样定理,能够以远少于传统方法所需的采样数来进行图像的精确重构。它在减少冗余数据、节省存储空间上有较大优势。因而,压缩感知掀起了信号处理领域的革命,被广泛应用于医用电子学、模式识别、数据采样与挖掘、无线通信、信道编码、天文学以及雷达遥感等领域。观测矩阵的设计是压缩感知研究的关键问题之一,构造性能好的观测矩阵对于观测值的获取和图像的精确重构都起到了至关重要的作用。目前,国内外提出的优化方法主要有:通过减小格拉姆矩阵(Gram)的非对角线元素增大观测矩阵与稀疏基之间的非相干性,从而实现观测矩阵的优化。用到的方法主要有等角紧框架法、梯度迭代法以及特征值优化方法[1,2,3,4,5,6,7,8,9,10,11]等;利用增强观测矩阵的列独立性实现观测矩阵优化[12,13]等等。上面提到的优化方法主要是通过减小观测矩阵与稀疏基之间的互相干性单方面展开[1,2,3,4,5,6,7,8,9,10,11],或者通过增大观测矩阵的列独立性展开[12,13]。文中将把增强观测矩阵的列独立性和增大观测矩阵与稀疏基之间的非相干性结合起来,寻求一个更加优化的观测矩阵,从而利用相同的观测个数,实现重构质量更好、仿真实验更稳定的效果。
1 压缩感知压缩感知(compressed sensing,CS)突破了香农采样定理的瓶颈,使高分辨率信号的采集成为可能,引起广大学者的研究。对压缩感知进行数学建模,它主要涉及3方面的内容[14]:
1)寻求稀疏基Ψ∈RN×N,并将信号X∈RN进行稀疏表示,由式(1)可以得到稀疏向量Θ∈RN:

2) 设计一个平稳的、与稀疏基ψ不相关的观测矩阵Φ∈RM×N,保证稀疏向量Θ能够从N维降到M维,同时不丢失重要信息,进而得到观测集合Y∈RM,如式(2)所示:

3) 设计快速重构算法,利用观测集合Y并根据式(3)恢复原信号:
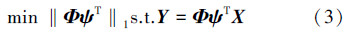
稀疏表示是指在某个特定变换域中用尽量少的基函数来尽可能完整地表示原始信号[15]。信号能够进行有效的稀疏表示是压缩感知的前提。所以,稀疏基的选择是压缩感知的先决条件。常用的稀疏基有DCT基、小波基、Chirplet基、Gabor基等,但是这些固定的正交基有时还不足以表示如声音或自然图像这些信号所具有的复杂未知规则性,不能保证信号在变换域足够稀疏。稀疏基的构造不是文中的研究重点,根据文中实验图像的特点,文中采用较常用的小波基。
观测矩阵进行的线性观测是把信号稀疏表示和信号重构连接起来的桥梁,观测矩阵的设计是压缩感知的重要部分[15]。提出了观测矩阵设计时应该满足的3个原则,根据这3个原则构造了一些常用观测矩阵,例如高斯矩阵、正交观测矩阵、多项式确定观测矩阵、循环矩阵、循环直积观测矩阵等。文中采用高斯矩阵作为基本矩阵。
常用的重构算法主要分为3类[16]:1) 贪婪追踪算法:匹配追踪算法、正交匹配追踪算法(OMP)、分段正交匹配追踪算法等;2) 凸松弛算法:梯度投影法、基追踪算法内点法等;3) 组合算法:傅立叶采样以及链式追踪等。文中采用OMP算法。
2 文中优化算法现有的观测矩阵几乎都存在着一些不足,目前观测矩阵的研究热点在于:寻找需要更少观测值的新矩阵;对观测矩阵进行优化,在相同观测数的情况下,使观测矩阵具有更好的性质;构造或优化能够减小计算复杂度和提高实验稳定性的观测矩阵。
为了利用更少的观测值得到更加精确、更加稳定的重构结果,文中结合观测矩阵列向量的独立性以及观测矩阵与稀疏基之间的非相干性两方面对观测矩阵进行优化,提出一种利用QR分解来增大观测矩阵的列独立性方法,同时提出通过优化Gram矩阵特征值增大观测矩阵与稀疏基之间的非相干性的优化方法(以下简称QT算法)。
2.1 QR分解增大列独立性观测矩阵的列独立性越大,重构所需的观测值越少,重构质量也越高。文献[19]中指出设计观测矩阵时,要保证观测矩阵的最小奇异值大于某一个大于零的常数。而文献[class="xref">20]中指出矩阵的最小奇异值与矩阵的列向量相关性密切相关。最小奇异值越大矩阵的列相关性越弱,列独立性越强。因此,观测矩阵的最小奇异值是影响图像重构质量的重要因素。所以,可以在不违背文献[15]中提出的观测矩阵应该满足的性质前提下,通过增大观测矩阵的最小奇异值对观测矩阵进行优化,最终会得到更好的重构效果。
QR分解优化不但能够增大矩阵的最小奇异值,同时能够保持矩阵的性质基本不变[16]。QR分解优化主要原理为:首先对观测矩阵Φ∈RM×N进行QR分解,得到正交矩阵Q∈RM×N和上三角矩阵A∈RN×N。然后对A分析,看出其主对角线元素远远大于非对角线元素,利用该发现,把A的非对角线元素全置零得A1,再根据A1得优化后的观测矩阵Φ1∈RM×N。通过QR分解优化,Φ的最小奇异值小于Φ1的最小奇异值[12]。
2.2 基于特征值的优化文献[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]提出观测矩阵与稀疏基之间的互相干性越小,重构所需的观测值越少,重构精度也越大。观测矩阵与稀疏基之间的互相干性μ(Φ,Ψ)如式(4)所示:
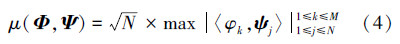
基于特征的优化算法是针对Gram矩阵的特征值进行的,算法的本质在于通过减小Gram矩阵的非对角线元素减小互相干性。
首先,构造D∈RN×N,令D=ΦΨ,其中观测矩阵Φ∈RM×N,并且秩为M,稀疏基Ψ∈RN×N。对D进行归一化得到D1,然后构造Gram矩阵G∈RN×N,令 。G的非对角线元素的大小和观测矩阵与稀疏基之间的非相干性的大小有着密切关系:非对角线元素越小,互相干性越小。文中通过使G的非对角线元素的平方和最小化实现互相干性最小化。
。G的非对角线元素的大小和观测矩阵与稀疏基之间的非相干性的大小有着密切关系:非对角线元素越小,互相干性越小。文中通过使G的非对角线元素的平方和最小化实现互相干性最小化。
对上面的G进行分析,假设G有M个大于0的特征值lk(k < M),根据矩阵的迹理论以及特征值的相关理论,加上G是归一化矩阵,求解观测矩阵和稀疏基之间最小相关性问题可以等价为求解式(5)的最优解。
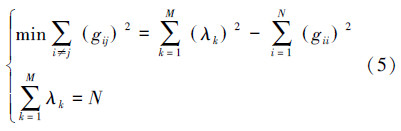
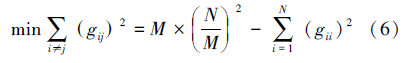
文中优化算法的主体思路是选择高斯随机矩阵为原始观测矩阵,利用它构造Gram矩阵,之后对Gram矩阵优化,让它的特征值逐渐逼近N/M。然后通过优化后的Gram矩阵反向求出此时的观测矩阵,并且对此时的观测矩阵进行QR分解优化,增大观测矩阵的列独立性。继续用求得的观测矩阵求解Gram矩阵,在不断地进行观测矩阵和Gram矩阵的相互求解过程中,当达到设置的终止条件时,输出此时的观测矩阵。通过上述优化后,观测矩阵不但列独立性得到了增强,而且它与稀疏基的非相干性也相应增大了。另外,由于每次迭代中QR分解优化时A只保留相对较大的主对角线元素,观测矩阵保存了主要信息,又因为G不断趋向于最优化矩阵,加上观测矩阵与Gram矩阵的不断相互求解,因此,每次得到的观测矩阵很相近,相应地,仿真结果稳定性也较好。
2.3 算法流程及具体实现通过算法分析,设计出QT算法流程如图 1。
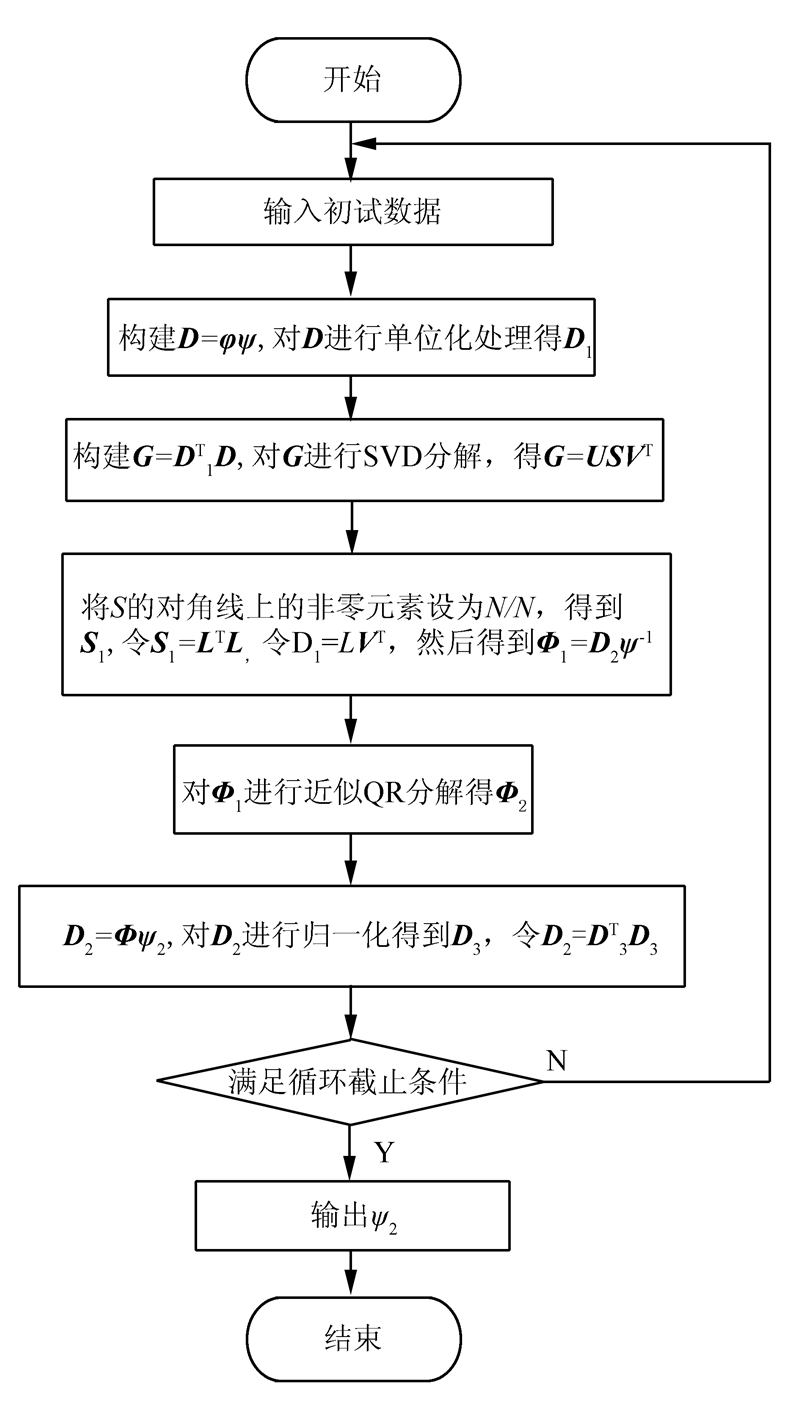 |
| 图 1 QT算法流程图Fig. 1 The flow of QT algorithm |
对上述流程进行细化,具体实现如下:
输入 Φ∈RN×NΨ∈RN×N,最大迭代次数设为100。
输出 优化后的观测矩阵Φ2。
具体实现步骤如下:
1) 构造D∈RM×N,并且令D=ΦΨ,对其进行归一化处理,得到归一化矩阵D1;
2) 由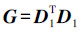 构造出Gram矩阵G,然后对G进行奇异值分解,即G=USVT,其中U,V均为酉矩阵,S为对角矩阵,并且U∈RN×N,V∈RN×N,S∈RN×N;
构造出Gram矩阵G,然后对G进行奇异值分解,即G=USVT,其中U,V均为酉矩阵,S为对角矩阵,并且U∈RN×N,V∈RN×N,S∈RN×N;
3) 将S中对角线上的非零元素置为N/M,得到S1,接着得到G1=US1VT;
4)根据S1=LTL,对S1进行分解,得到矩阵L。其中L∈RM×N,并且它的对角线元素为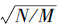 ,其他元素为零;
,其他元素为零;
5)设D2∈RM×N,并且令D2=LVT,然后通过Φ1=D2Ψ-1,求得Φ1;
6)对Φ1进行近似QR分解的优化:即首先对Φ1进行QR分解,得到Φ1=EF。其中,正交阵E∈RM×N,而上三角矩阵F∈RM×N;然后将F中的非对角线元素设置为零,得到F1;最后根据Φ2=EF1,求得进一步更新的观测矩阵Φ2;
7)利用D2=Φ2Ψ求出D2,接着对D2进行归一化处理,得到D3,然后继续利用 得到新的Gram矩阵G2,求出G2中除主对角线元素外的所有值的平方和(sum),当(sum)-((N/M)2-N)| < 0.1时,输出此时的观测矩阵Φ2,否则跳转到②继续新的循环。
得到新的Gram矩阵G2,求出G2中除主对角线元素外的所有值的平方和(sum),当(sum)-((N/M)2-N)| < 0.1时,输出此时的观测矩阵Φ2,否则跳转到②继续新的循环。
为了验证文中算法的有效性,文中选择多幅自然图像,应用文中提出的算法进行观测矩阵的构造,然后对观测数据,采用OMP算法进行重构,将重构图像的信噪比和目前的经典算法进行比较。
采用256×256的自然图像,初始的观测矩阵采用高斯矩阵,稀疏基选取小波基,重构算法选取OMP算法。进行对比算法的观测矩阵分别是初始高斯矩阵,经QR分解优化的高斯矩阵[12],基于特征值优化的高斯矩阵[11]。实验部分分为2个部分:对比不同的观测长度下,不同观测矩阵得到的重构精度的比较(多次重构的平均结果);比较在相同观测长度下,不同观测矩阵得到的重构精度(单次重构的结果)。
3.1 不同观测长度的比较为了验证文中构造的观测矩阵的有效性,对于同样一幅自然图像,分别选取不同的观测矩阵长度M,比较采用不同观测矩阵得到的观测向量的重构精度,并用信噪比表示。由于观测矩阵选取的随机性,所以每次结果都不尽相同。
为得到一个统计性的结果,采用50次平均的结果为最终结果。表 1、2分别表示4种方法在不同观测个数时lena和cameralman重构图像的信噪比。
| dB | ||||
|
观测 矩阵 |
高斯 矩阵 |
QR分解 优化 |
特征值 优化 |
QT 算法 |
| m=80 | 18.395 | 18.607 | 21.644 | 29.205 |
| m=100 | 26.197 | 26.572 | 27.317 | 31.086 |
| m=120 | 28.190 | 28.581 | 29.444 | 32.902 |
| m=140 | 29.805 | 30.334 | 31.640 | 34.151 |
| m=160 | 31.384 | 32.077 | 33.375 | 35.115 |
| dB | ||||
|
观测 矩阵 |
高斯 矩阵 |
QR分解 优化 |
特征值 优化 |
QT 算法 |
| m=80 | 16.942 | 16.994 | 19.547 | 25.070 |
| m=100 | 22.210 | 22.551 | 23.322 | 26.423 |
| m=120 | 23.398 | 24.063 | 24.809 | 27.760 |
| m=140 | 25.629 | 25.629 | 26.401 | 28.661 |
| m=160 | 27.111 | 27.112 | 28.275 | 29.441 |
由表 1和表 2中的数据可以看出,经QR分解优化后,PSNR相对于未经优化时提高的幅度不明显,而经过特征值优化后,PSNR相对于未经优化时提高的幅度较大。将QT算法和前3种算法中效果最好的基于特征值优化算法相比较:当M=80、100、120、140、160时,lena的PSNR提高情况分别为7.6、3.8、3.5、2.5和1.8 dB,而cameraman的PSNR提高情况分别为6.5、3.1、2.9、2.2与1.2 dB。通过比较分析,随着M的增大,文中方法的优势越来越小,也就是说M越小,优化算法优势更大。总的来说,文中优化方法在保证近似精确重构的条件下,减小观测次数上更有空间。
3.2 算法的鲁棒性比较由于观测矩阵的初始矩阵均为高斯噪声,因此每次仿真试验的初始矩阵都是随机的,从而每次重构的结果都会有所差异。由于QT算法同时考虑了观测矩阵列的独立性,以及观测矩阵和基函数的不相关性,因此,比其他3种算法有更好的鲁棒性。依然选取lena和cameraman2幅图像进行图示对比。图 2和图 3分别为当M=80时对2幅图像进行观测重构之后的单次重构精度的曲线图。
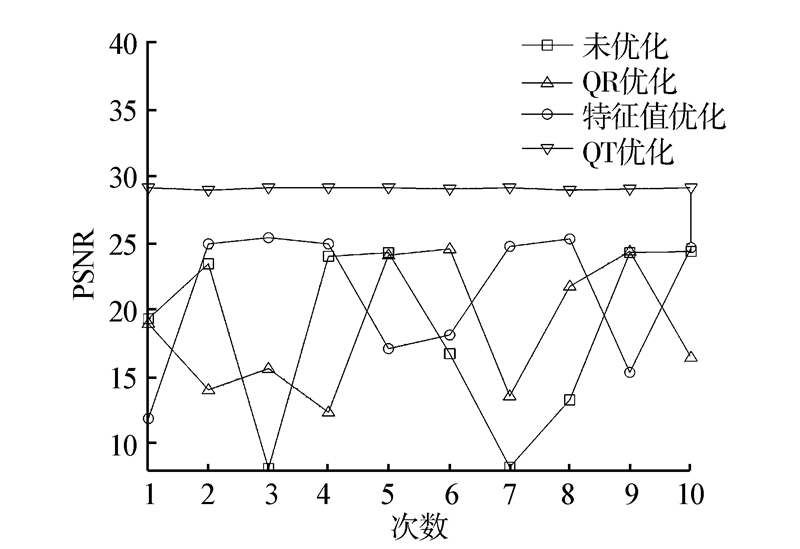 |
| 图 2 M=80时的PNSR图(lena)Fig. 2 The graph of PNSR when the value of M is 80(lena) |
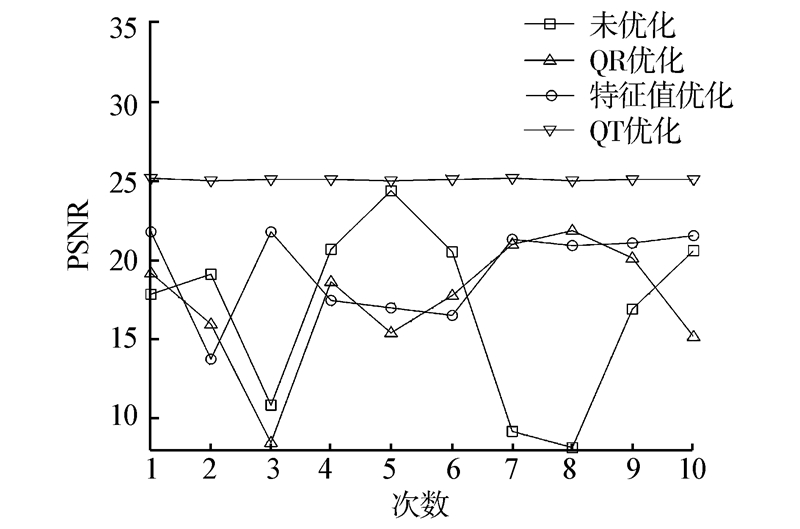 |
| 图 3 M=80时的PNSR图(cameraman)Fig. 3 The graph of PNSR when the value of M is 80(cameraman) |
由图 2、3可以看出:当M=80时,其他3种方法的PSNR变化幅度比较大,而且经QR分解优化和特征值优化后的PSNR值在个别点上比未经优化时小。文中优化方法每次的PSNR始终大于其他3种方法,并且每次它的波动在5%以内,稳定性较好。另外,随着观测值的增多,其他方法的实验仿真稳定性也会有所提高,和文中优化算法在稳定性上的趋势比较接近。由上述实验可以得到结论:当观测值较少时,文中提出的优化算法无论在PSNR,还是实验结果的稳定性上,都比其他3类算法有更好的效果。图 4和图 5给出了lena和cameraman在M=120时的4种算法的重构结果。
 |
| 图 4 不同方法优化的重构图(lena)Fig. 4 The reconstructed images by different optimization methods(lena) |
 |
| 图 5 不同方法优化的重构图(cameraman)Fig. 5 The reconstructed images by different optimization methods(cameraman) |
从对图 4和图 5进行分析可以看出,M=120时,经QR分解优化效果不大。基于特征值优化的重构图相对前2种方法在帽子边缘和头发、脸部这些细节部分明显变得更清晰,重构质量得到了较大提高。文中算法优化的重构图在鼻子、嘴巴以及眼睛这3个细节处的重构效果更好。综合以上分析,文中算法在相同的观测个数时,重构质量更高。
4 结束语文中提出的优化算法,紧密结合观测矩阵的列独立性和观测矩阵与稀疏基的非相干性两方面对观测矩阵进行优化。通过对实验结果进行分析,文中提出的优化算法在重构质量和稳定性这2个方面有较大优势,尤其在观测个数较少时,优势更明显。后期的工作将尝试研究确定性观测矩阵,如何采用更少的观测个数,得到更精确的重构结果是下一步的研究目标。
| [1] | ELAD M.Optimized projections for compressed sensing[J].IEEE Transaction on Signal Processing,2007,55(12):5695-5702. |
| [2] | DINH M N.Efficientprojection for compressed sensing[C]//7th ACIS International CONFerence on Computer and Information Science.Oregon,America,2008:322-327. |
| [3] | JULIO M D,GUILLERMO S.Learning to sense sparse signals:Simultaneous sensing matrix and sparsifying dictionary optimization[J].IEEE Transactions on Image Processing,2009,18(7):1395-1408. |
| [4] | CAO Z.Optimized projection matrix for compressive sensing[J].EURAIP Journal Advances in Signal Processing,2010(43):55-60. |
| [5] | YU Lifeng,LI Gang,CHANG Liping.Optimizing projection matrix for compressed sensing systems[C]//8th International Conference on Communnicationand Signal Processing,2011:1-5. |
| [6] | EVAGGLIAT,LISIMACHOS P K,AGGELOS K K.Useof tight frames for optimized compressed sensing[C]//20th European Signal Processing Conference,Bucharest,2012:1439-1443. |
| [7] | VAHID A,SAIDEH F,SAEID S.A gradient-based alternating minimization approach for optimization of measurement matrix in compressive sensing[J].Signal Processing,2012,92(4):999-1009. |
| [8] | THONG T D,LU Gan,NAM H N,et al.Fast and efficientcompressive sensing using structurally random matrices[J].IEEE Transactions on Signal Processing,2012,60(1):139-154. |
| [9] | WEI Chen,MIGUEL R D.On the use of unit-norm tight frames to improve the use of MSE performance in compressive sensing application[J].Transactions on Signal Processing Letter,2012,19(1):8-11. |
| [10] | TSILIGIANNI E,KONDI L P,KATSAGGELOS A K.Use of tight frames for optimized compressed sensing[C]//20th European Signal Processing ConferenceBucharest,2012:1439-1443. |
| [11] | 赵瑞珍,秦周,胡绍海.一种基于特征值分解的测量矩阵优化方法[J].信号处理,2012,28(5):653-658.Zhao Ruizhen,QIN Zhou.An method based on eigenvalue decomposition to optimize measurement matrix[J].Signal Processing,2012,28(5):653-658. |
| [12] | 傅迎华.可压缩传感重构算法与近似QR分解[J].计算机应用,2008,28(9):2300-2302.FU Ying hua.Reconstruction algorithm of compressed sensing and QR decomposition[J].Computer Applications,2008,28(9):2300-2302. |
| [13] | 彭玉楼,何怡刚,林斌.基于奇异值分解的压缩感知噪声信号重构算法[J].仪器仪表学报,2012,33(12):2655-2660.PENG Yulou,YI Gang,LIN Bin.Reconstruction algorithm of compressed sensing noise signal based on singular value decomposition[J].Journal of Scientific Instrument,2012,33(12):2655-2660. |
| [14] | DONOHO.Compressed sensing[J].IEEE Trans on Information Theory,2006,52(4):1289-1306. |
| [15] | YAAKOV TSAIG,DAVID L.Extensions of Compressed sensing[J].Signal Processing,2006,86(3):533-548. |
| [16] | DAVID L.Compressed sensing[J].Information Theory,2006,52(4):1289-1306. |



